Сигма-дельта АЦП 4-го порядка

это высокоточный аналого-цифровой преобразователь (АЦП), который достигает исключительного разрешения (часто 16-24 бита и более) за счет двух ключевых приемов:

Сильно загрублённого, но очень быстрого 1-битного АЦП (компаратора) внутри.
Сложной цифровой фильтрации 4-го порядка, которая "вылавливает" полезный сигнал из огромного количества шума, создаваемого этим грубым АЦП.

"4-й порядок" указывает на степень сложности и эффективности внутренней системы шумоподавления.

Сигма-дельта АЦП 4-го порядка — это инструмент для прецизионных измерений:

Прецизионные измерительные приборы: Мультиметры, анализаторы спектра.
Медленная телеметрия и датчики: Датчики температуры, давления, нагрузки (тензодатчики), особенно в промышленных и медицинских приборах.
Аудиотехника высокого класса (Hi-Fi, студийное оборудование): Для оцифровки звука с минимальными искажениями.
Взвешивание: Торговые и лабораторные весы высшего класса.
Сейсморазведка и геофизика: Где нужна запись слабых низкочастотных сигналов.

С принципами работы "базового" сигма-дельта ЦАП первого порядка вы можете ознакомиться в этом примере. И почитать вот эту статью для более глубокого понимания его принципов работы.

А в данном проекте мы рассмотрим динамическую модель более сложной схемы аналого-цифрового преобразователя, и сравним два типа децимирующих фильтров нижних частот, применяемых в подобных устройствах.

Структура АЦП

Рассмотрим верхний уровень модели SDADC_4thORD.engee:

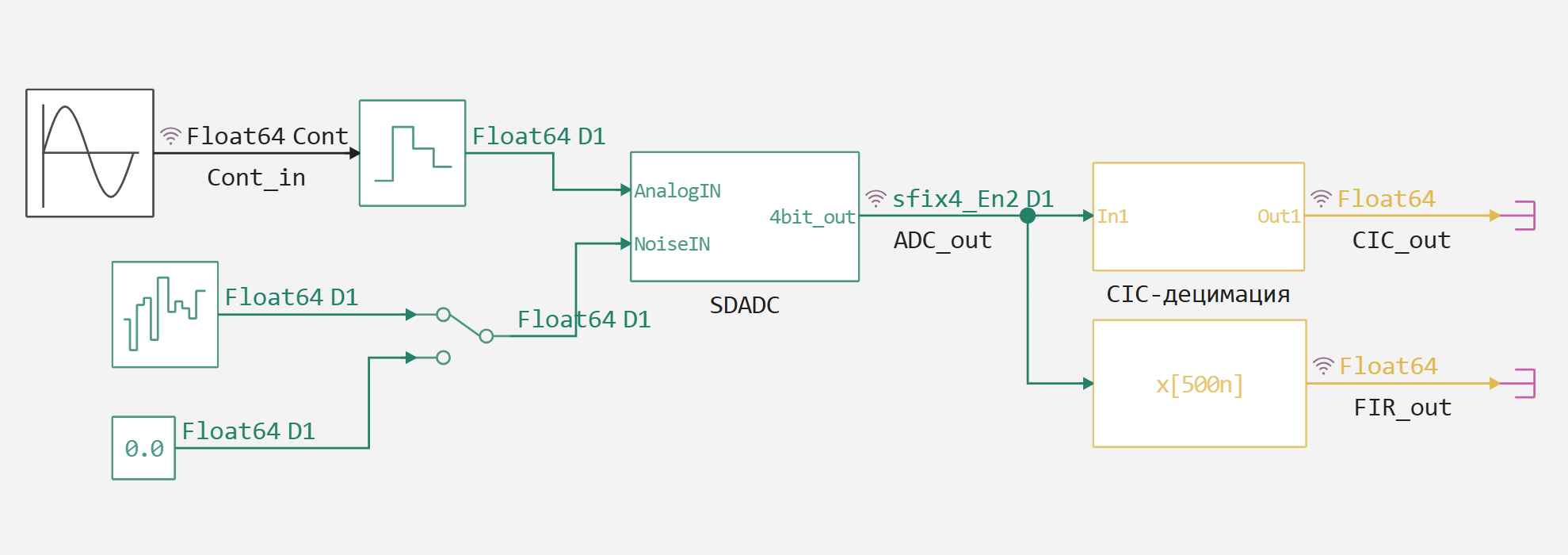
В качестве источника тестового сигнала используется блок непрерывной синусоиды, который генерирует два периода на отрезке времени в 0.02 секунды - то есть основная частота колебания составляет 100 Гц. Затем этот сигнал проходит операцию дискретизации с частотой в 1 МГц.

Выбор настолько завышенной частоты дискретизации - стандартная практика при использовании сигма-дельта АЦП. В данном случае, для успешного восстановления сигнала с основной частотой 100 Гц хватило бы брать его дискретные отсчёты с частотой не ниже 200 Гц. Но в рассматриваемой модели для сохранения относительно плавной формы цифрового синусоидального сигнала было решено взять запас в 10 раз превышающий требование теоремы Котельникова, то есть выходная частота дискретизации сигнала должна равняться 2 кГц.

Поэтому непосредственно после выхода блока SDADC, сигнал разрядностью 4 бита и частотой дискретизации в 1 МГц попадает на дециматоры, которые выполнены на базе CIC-фильтра и FIR-фильтра. Обе этих цепи понижают частоту дискретизации сигнала в 500 раз. Параметры блока КИХ-дециматора:

И структура подсистемы CIC-дециматора:

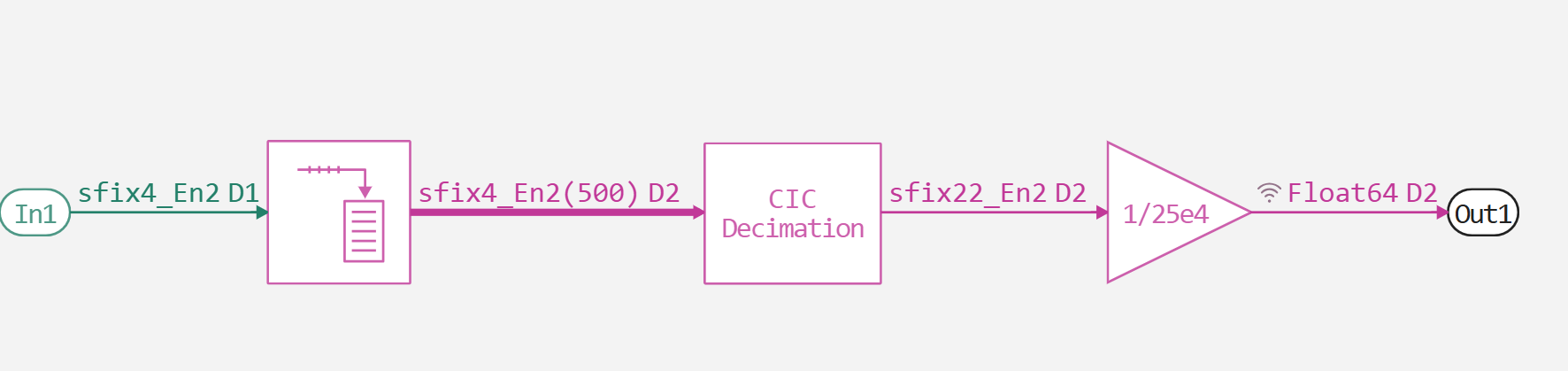
Схема преобразователя 4-го порядка

Подсистема SDADC содержит обобщённую структуру преобразователя 4-го порядка с возможностью моделирования аддитивного шума:

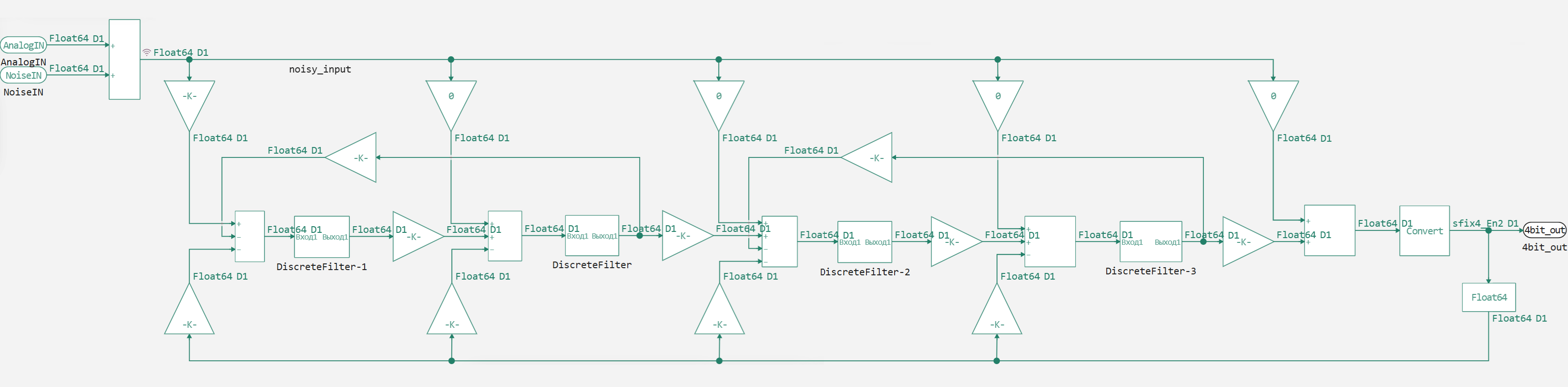
В данном случае в качестве квантователя на выходе схемы используется блок "Преобразования типов данных", выдающий знаковый четырёхбитный сигнал. Также на схему можно подавать белый шум с ограниченной полосой, для оценки влияния искажений сигнала на результат оцифровки.

Симуляция модели

При запуске модели на динамическую симуляцию в окне "Визуалиация сигналов" можно наблюдать как непрерывный входной сигнал, так и сравнение выходов двух децимирующих фильтров:

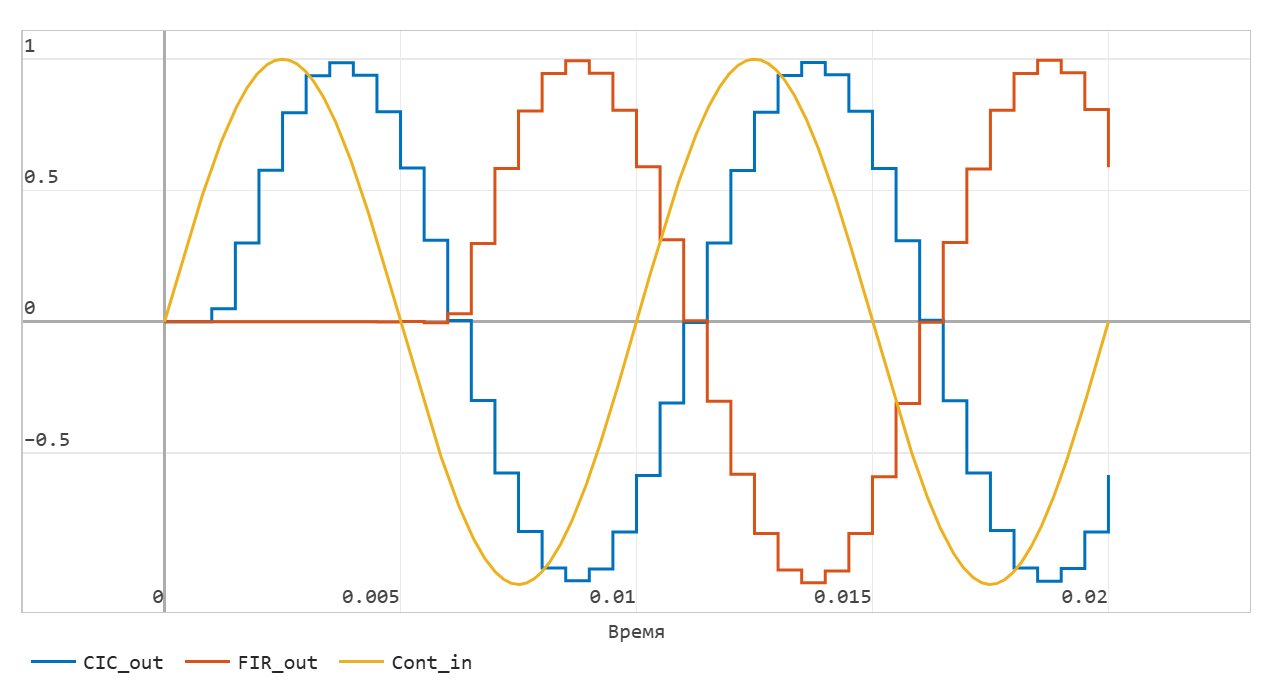
Мы видим, что КИХ-фильтр столь большого порядка вносит существенную задержку, но форма дискретных синусоид идентична.

Программный анализ результатов симуляции

Запустим модель программно и проанализируем логируемые сигналы во временной и частотной областях. Сохраним все сигналы в переменную result:

demoroot = @__DIR__
mdl = engee.open(joinpath(demoroot,"SDADC_4thORD.engee"))
result = engee.run(mdl);

Отобразим зашумлённый вход и чеырёхбитный выход подсистемы SDADC во времени:

noisy_input = collect(result["noisy_input"]);
ADC_out = collect(result["ADC_out"]);
plot(ADC_out.time,ADC_out.value,l=:steppost, label="ADC_out")
plot!(noisy_input.time,noisy_input.value,lw=3, label = "noisy_input")

Интересная особенность в спектре сигнала на выходе подобной схемы: шум, порождаемый грубостью 1-битного квантования, не исчезает, но форма спектра этого шума изменяется системой обратной связи. Он "выталкивается" (подавляется) в низкочастотной части спектра и усиливается на высоких частотах. Поскольку наш полезный сигнал — низкочастотный, цифровой фильтр легко отсекает этот сдвинутый высокочастотный шум.

Рассмотрим сигнал ADC_out в частотной области:

using EngeeDSP.Functions
p,f = pspectrum(ADC_out.value,1e6);
plot(f,10log10.(p),title="Спектр на выходе 4-битного АЦП")

И рассмотрим спектр сигнала на выходе децимирующего CIC-фильтра:

CIC_out = collect(result["CIC_out"]);
periodogram(CIC_out.value, NFFT = 2048, fs = 2e3)

Заключение

Мы рассмотрели модель сигма-дельта АЦП 4-го порядка, который использует 4-интеграторную структуру и цифровую фильтрацию для достижения рекордного соотношения "точность/стоимость" в приложениях, где важна не скорость, а чистота и разрешение оцифрованного низкочастотного сигнала.

Сигма-дельта АЦП 4-го порядка