Локализация целей на основе активных РЛС

В этом примере показано, как моделировать сценарий работы активных радиолокационных систем (РЛС) и определять оценки времени задержки распространения сигнала (TOA) для решения задачи локализацию при наличии малоразмерной цели.

Этот пример — первая часть серии решений задачи локализации. Вторая часть посвящена методу пассивной радиолокации с применением алгоритма TDOA (Time Difference Of Arrival) для локализации самолета.

Введение

В области радиолокации задача локализации цели на основе данных, полученных от группы пространственно разнесённых датчиков с известными координатами, имеет значительную актуальность. Для решения этой задачи традиционно применяются методы, основанные на измерениях времени прихода (TOA — Time Of Arrival) и разности времён прихода (TDOA — Time Difference Of Arrival) сигналов.

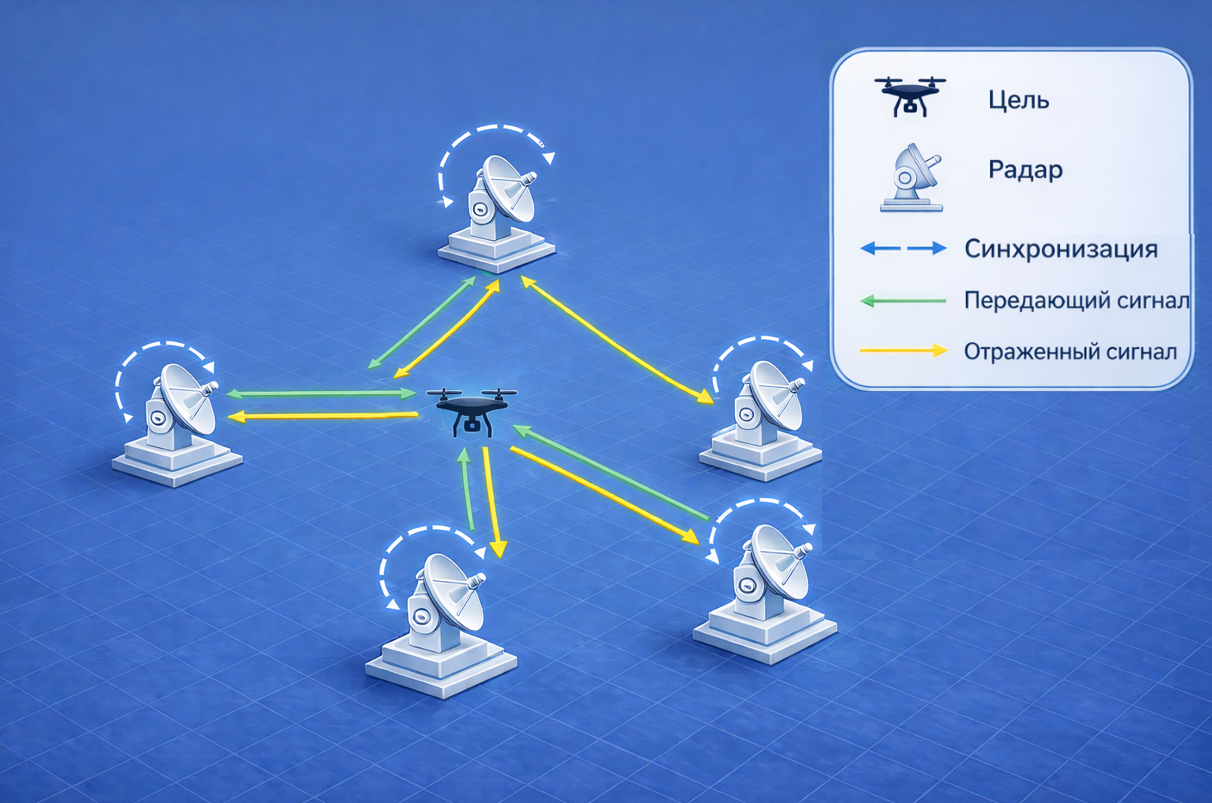
Локальное позиционирование целей с помощью РЛС может быть реализовано в различных конфигурациях. Одной из наиболее распространенных конфигураций является моностатическая активная радиолокационная система, которая определяет местоположение цели путем активной передачи радиолокационных сигналов и последующего приема отраженных сигналов с помощью совмещенного и синхронизированного передатчика и приемника (см. рисунок ниже).

В такой радиолокационной системе TOA определяется на основе задержек распространения сигнала между целью и радиолокационным приемопередатчиком.

Подключение вспомогательных функций

Выполним инициализацию функций, необходимых для расчета оценок позиционирования и визуализации методов локализации TOA

Pkg.add("DSP")
isdefined(Main,:init_func) || include("init.jl")

Рассмотрим локализацию (TOA) цели на основе системы моностатических активных РЛС. Каждая из РЛС имеют синхронизированные приемник и передатчик.

1. Формирование сценария работы РЛС

Создадим сценарий работы 5 радаров X-диапазона, имеющих известные координаты, для локализации беспилотного летательного аппарата (БПЛА) с малой эффективной площадью рассеяния (ЭПР).

# Параметры РЛС
fc = 9e9 # [Гц], несущая частота
c = physconst("LightSpeed") # [м/с], скорость распространения сигнала
bw = 200e6 # Гц, полоса сигнала
fs = bw # Гц, частота дискретизации

# Параметры приемо-передающего тракта
Pt = 1 # Вт, пиковая мощность
Gtx = 40 # дБ, усиление передающей антенны
Grx = 40 # дБ, усиление приемной антенны
NF = 2.9 # дБ, коэффициент шума приемного тракта

# Формирование системных объектов (СО) функциональных узлов РЛС
antenna = EngeePhased.IsotropicAntennaElement( # СО изотропного антенного элемента
    BackBaffled=false # учет обратного рассеяния ДН антенны
) 
transmitter = EngeePhased.Transmitter( # СО - передатчик
    Gain=Gtx, # усиление передатчика
    PeakPower=Pt # Пиковая мощность 
)
radiator = EngeePhased.Radiator( # СО - передающая антенна
    Sensor=antenna, # ДН антенного элемента
    OperatingFrequency=fc # несущая частота антенны
)
collector = EngeePhased.Collector( # СО - приемная антенна
    Sensor=antenna, # ДН антенного элемента
    OperatingFrequency=fc # несущая частота антенны
)
receiver = EngeePhased.ReceiverPreamp(
    Gain=Grx, # усиление приемника
    NoiseFigure=NF, # коэффициент шума в тракте
    SampleRate=fs # частота дискретизации
)

# Создание СО - цель
tgtrcs = 1e-2 # м^2, ЭПР цели
target = EngeePhased.RadarTarget(
    MeanRCS=tgtrcs, # среднее значение ЭПР
    PropagationSpeed=c, # скорость распространения сигнала
    OperatingFrequency=fc # несущая частота сигнала
)

# Модель сценария движения цели
tgtpos = [30; 10; 15]; # [pos_x,pos_y,pos_z],м начальный вектор положения цели 
tgtvel = [5; 10; 0]; # [v_x,v_y,v_z],м/с вектор скорости цели 
tgtplatform = EngeePhased.Platform( # СО - модель движения цели
    InitialPosition=tgtpos,  # начальный вектор положения цели 
    Velocity=tgtvel # вектор скорости цели 
) 

# Модель сценария движения РЛС
radarpos = [   # м, начальные положения РЛС    
    0 -30. 100 80 -40; 
    0 50 -40 30 -20; 
    0 -5 7 5 2
]                        
numRadar = size(radarpos,2) # Число РЛС 
radarvel = zeros(3,numRadar) # [v_x,v_y,v_z] [м/с], скорости РЛС
radarplatform = EngeePhased.Platform( # СО - модель движения РЛС
    InitialPosition=radarpos,  # начальный вектор положения  
    Velocity=radarvel # вектор скорости РЛС 
);

2. Формирование зондирующего сигнала (ЗС)

Одним из самых популярных сигналов для радиолокационных систем является непрерывный частотно-модулированный сигнал или FMCW-сигналы. FMCW-сигналы широко используются в радиолокационных системах, поскольку этот метод хорошо отработан и не требует больших затрат.

# Формирование непрерывного сигнала с ЛЧМ
N = 1024 # число отсчетов за время нарастания (отсчеты быстрого времени )
M = 8 # количество импульсов накопления (отсчеты медленного времени)
freqSpacing = bw/N # Гц, разрешение по частоте
tWave = N/fs; # с, время нарастания пилы (длительность импульса)
fmcwWaveform = EngeePhased.FMCWWaveform(  # системный объект FMCWWaveform
    SweepTime=tWave, # длительность импульса
    SweepBandwidth=bw, # полоса сигнала (ширина спектра)
    SampleRate=fs, # частота дискретизации
    SweepDirection="Up" # направление изменения частоты
)

# Моделирование непрерывного ЛЧМ сигнала для М-каналов
sig_lfm = ComplexF64.(fmcwWaveform()*ones(1,M))
println("Размерность ЗС: $(size(sig_lfm))")

Размерность ЗС: (1024, 8)

Применим функцию plot_sig_and_spec для построение графика осциллограммы и спектрограммы непрерывного сигнала с ЛЧМ:

plot_sig_and_spec(sig_lfm[:,1];fs=fs,name_sig = "непрерывного ЛЧМ")

На спектрограмме можно пронаблюдать изменение частоты от 0 до 200 МГц за 5 мкс, что соответствует заданным требованиям по девиации частоты `bw` и длительности импульса `tWave` генератора

3. Канал распространения

В рассматриваемом сценарии моделью канала распространения сигнала является свободное пространство между каждой РЛС и целью в условиях отсутствия взаимных, пассивных и активных радиолокационных помех. Для реализации модели воспользуемся системным объектом EngeePhased.FreeSpace, позволяющий учесть затухание при распространении на несущей частоте, доплеровское смещение при наличии относительного движения цели и двунаправленное распространение (до цели и обратно).

# Формирование канала распространения сигнала с учетом двунаправленного распространения
channel = EngeePhased.FreeSpace( # СО - модель канала (свободное пространство)
    PropagationSpeed=c, # скорость распространения
    OperatingFrequency=fc, # несущая частота
    SampleRate=fs, # частота дискретизации
    TwoWayPropagation=true # учет двунаправленного распространения
)

FreeSpace:
    PropagationSpeed=299792458
    OperatingFrequency=9.0e9
    SampleRate=2.0e8
    TwoWayPropagation=true
    MaximumDistance=10000.0

4. Расчет сценария работы активной системы РЛС

После инициализации системных объектов, необходимых для расчета сценария работы системы, выполним расчет отраженного сигнала от БПЛА для каждой РЛС. Суммарный отраженный сигнал будем хранить в переменной X с размерностью [N,M,R]:

N — количество отсчётов в быстром времени,

M — количество импульсов в медленном времени.

R — количество РЛС в активной системе.

# Создание опорного сигнала
refsig = deepcopy(sig_lfm[:,1])

# Выделение памяти под отраженный сигнал для всех РЛС
X = zeros(ComplexF64,size(sig_lfm)...,numRadar)

# Сигнал после передатчика
txsig = transmitter.(sig_lfm)

for rad_i in 1:numRadar
    # Инициализация входного сигнала 
    x = zeros(ComplexF64,size(sig_lfm))

    # Приемо-передающий тракт
    for m in 1:M
        # Обновление положения цели и РЛС
        radar_pos,radar_vel = radarplatform(tWave)
        tgt_pos,tgt_vel = tgtplatform(tWave)

        # Расчет углов пеленга передающего устройства
        _,txang = rangeangle(tgt_pos,radar_pos[:,rad_i]) 

        # Излучение ЗС в пространство
        radtxsig = radiator(txsig[:,m],txang) 

        # Распространение сигнала в пространстве
        chansig = channel(
            radtxsig,radar_pos[:,rad_i],
            tgt_pos,radar_vel[:,rad_i],tgt_vel
        )

        # Отражение сигнала от цели
        tgtsig = target(chansig)

        # Расчет углов пеленга приемного устройства
        _,rxang = rangeangle(radar_pos[:,rad_i],tgt_pos)

        # Прием отраженного сигнала антенной
        rxsig = collector(tgtsig,rxang)

        # Предварительное усиление приемника
        x[:,m] .= receiver(rxsig)
    end

    dechirpsig = dechirp(x,refsig)
    X[:,:,rad_i] = conj.(dechirpsig)

    # Сброс положения РЛС и цели для расчета отраженного для следующей  РЛС
    reset_plt!(radarplatform,radarpos)
    reset_plt!(tgtplatform,tgtpos)
end

5. Расчет оценок задержки сигнала и локализация цели

После расчета отраженного сигнала для каждой РЛС следующим шагом является получение измерений времени прихода сигнала. Воспользуемся объектом TOAEstimator для оценки времени прихода сигнала, настроив Measurement="TOA". Метод спектрального анализа можно настроить как FFT, так и MUSIC.

spectrumMethod = "FFT"; # @param ["FFT", "MUSIC"]

# Формирование объекта TOAEstimator
toaEstimator = TOAEstimator(
    PropagationSpeed=c, # скорость распространения
    Measurement="TOA", # метод локального позиционирования 
    SpectrumMethod=spectrumMethod,  # спектральный метод
    VarianceOutputPort=true, # включение выхода СКО ошибки задержки
    SpatialSmoothing=ceil(Int64,N/2) # для алгоритм MUSIC
);

Выполним вызов объекта "toaEstimator" для расчета вектора задержек Y1 и вектора дисперсии var1

# Расчет оценок задержек и дисперсии
Y1,toa_var1 = toaEstimator(X,freqSpacing)
println("Оценки задержек для каждой РЛС: $(round.(Y1.*1e9;sigdigits=6)) нc")

Оценки задержек для каждой РЛС: [235.0, 500.0, 575.0, 365.0, 515.0] нc

# Построение спектра отраженного сигнала с пересчетом в задержку распространения
plotTDOASpectrum(
    toaEstimator, # объект расчета задержек
    anchorIdx=1:5, # Номера РЛС для отображения
    MaxDelay=700e-9, # Предел по оси задержек
    DinRange=30, # Динамический диапазон СПМ
    OneSidedSpectrum=true # построение одностороннего спектра
)

Получив оценки времени прохождения сигнала в одну сторону, дисперсии оценок времени прохождения сигнала и известные координаты радара, воспользуемся функцией toaposest для определения местоположения цели.

Поскольку полученные оценки времени прохождения сигнала представляют собой оценки задержки распространения сигнала в обе стороны, разделим оценки задержки распространения сигнала на 2, и оценки дисперсий времени прохождения сигнала на 4:

# Корректировка с учетом двунаправленного распространения
Y_single = Y1 ./ 2 # задержка, с
var_single = toa_var1 ./ 4 # дисперсия, с^2

# Расчет оценки положения цели
tgtposest = toaposest(Y_single,var_single,radarpos)

println("Оценка положений $(round.(tgtposest;sigdigits=6)) м")
println("Истинное положение $(tgtpos) м")

Оценка положений [30.1159, 9.97406, 15.2852] м
Истинное положение [30, 10, 15] м

Ниже приведена визуализация процесса локализации методом TOA:

helperPlotTOAPositions(c,Y_single,tgtposest,radarpos,tgtpos)

Мы также можем проверить точность определения местоположения с помощью среднеквадратичной ошибки (RMSE).

# Расчет СКО позиционирования
RMSE = rmse(tgtposest,tgtpos)
println("СКО позиционирования: $(round(RMSE;sigdigits=6)) м")

СКО позиционирования: 0.178337 м

Заключение

В примере продемонстрировано решение задачи локализации малоразмерной цели с применением активной многопозиционной РЛС в среде моделирования Engee.

Данная система представляет собой систему моностатических активных радаров, использующих непрерывный сигнал с линейной частотной модуляцией (FMCW). Реализованы методы оценки времени задержки распространения сигнала (TOA) с последующей локализацией источника сигнала на основе функций TOAEstimator и toaPosest.

Локализация целей на основе активных РЛС