Модель механического акселерометра
using ControlSystems
using LinearAlgebra
Сравнение моделей электромеханической измерительной головки (вольтметра) и электромеханического акселерометра
В данной статье расскажу про связь конструкции электро-механической измерительной головки (как на рисунке 1) и механического компенсационного акселерометра, полную версию статьи можно посмотреть по ссылке https://habr.com/ru/articles/980148/

Рисунок 1 - функциональная схема электромеханической измерительной головки
1 – стрелка для индикации измеренного напряжения.
2 – крепления рамки.
3 – рамка с катушкой.
4 – постоянный магнит.
5 – кольцевой магнитопровод.
6 – пружина (всего их две).
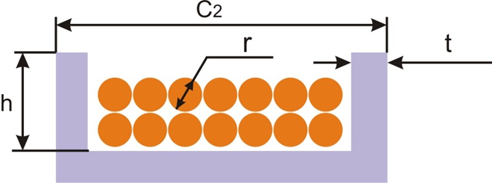
Рисунок 2 - Сечение рамки измерительной головки вольтметра.
Размеры рамки вольтметра
# Радиус провода намотанного в катушке:
r = 0.025*10^-3
# Внутренние размеры окна рамки:
a1 = 13.6*10^-3
b1 = 6.4*10^-3
# Внешние размеры окна рамки:
a2 = 15*10^-3
b2 = 7.8*10^-3
# Ширина рамки:
c2 = 4.2*10^-3
# Ширина бортика у рамки:
t = 0.3*10^-3
# Высота бортика у рамки:
h = 0.3*10^-3
# Максимальный угол отклонения рамки:
alpha_max = 0.411
# Длина стрелки:
Lc = 60*10^-3
# Ширина стрелки:
bc = 1*10^-3
# Толщина стрелки:
hc = 0.5*10^-3
.png)
Рисунок 3 - Положение рамки относительно магнита.
#Плотность алюминия (материал из которого сделана рамка):
ro1 = 2690
#Плотность меди (материал из которого сделан провод):
ro2 = 8930
Расчет геометрии рамки вольтметра
a3 = (a1+a2)/2
b3 = (b1+b2)/2
#Периметр:
R = a3*2+b3*2
#Площадь окна рамки:
S = a3*b3
# Площадь сечения рамки акселерометра:
s = c2*h-(c2-t*2)*(h-t)
#Объём применяемого в каркасе алюминия:
V = s*R
#Коэффициент заполнения при намотке привода:
p = 0.6
#Количество слоёв провода в катушке:
n = 10
#Зная ширину рамки и радиус провода, вычисляю количество витков провода в одном слое:
k = (c2-2*t)/(2*r)
#Помножаю это число витков на коэффициент заполнения:
k = floor(k*p)
#Далее посчитаю количество витков в катушке:
W = k*n
#Объём применяемой в катушке меди:
V2 = pi*r*r*R*W
#Объём применяемого в стрелке алюминия:
Vc = Lc*bc*hc
Расчет массы элементов рамки вольтметра
#Масса каркаса рамки:
m1 = ro1*V
#Масса медного провода в катушке:
m2 = ro2*V2
#Масса стрелки:
mc = ro1*Vc
#Масса короткой балки:
m3 = m1*b3/R+m2*b3/R
#Масса длинной балки:
m4 = m1*a3/R+m2*a3/R
Расчет моментов инерции рамки вольтметра
J1 = (2*m4*a3*a3)/12
#Момент инерции коротких балок:
J2 = 2*m3*(a3/2)^2
#Момент инерции стрелки:
Jc = 2*m3*(a3/2)^2
#Суммарный момент инерции рамки с катушкой и стрелки:
J3 = J1+J2+Jc
Расчет электрических параметров рамки вольтметра
#Индукция магнита:
B = 0.3
#Плотность тока в катушке:
ji = 1
#Удельное сопротивление алюминия:
ro_al = 0.0271
#Удельное сопротивление меди:
ro_m = 0.0175
#Ток в катушке:
I = pi*(r*1000)*ji
#Угловая жесткость пружин в подвесе:
C = (B*S*W*I)/alpha_max
#Электрическое сопротивление каркаса рамки:
Ral = R*ro_al/(s*10^6)
#Коэффициент электрического демпфирования при угловом движении рамки:
Kd = (B*B*S*S*I)/Ral
#Собственная частота колебаний измерительной головки вольтметра:
w0 = sqrt(C/J3)
f0 = w0/(2*pi)
Передаточная функция вольтметра
W1 = tf(1,[J3, Kd, C])
#Для проверки устойчивости можно применить например критерий Гурвица
a0 = J3
a1 = Kd
a2 = C
det([a1 0;
a0 a2] )
Частотная характеристика вольтметра
bodeplot(W1)
Годограф Найквиста для передаточной функции вольтметра
nyquistplot(W1) # годограф найквиста
Переходный процесс вольтметра
y, t = step(W1,0:0.01:1) # расчет переходного процесса
t = collect(0:0.01:1)
plot(t,y',title="Переходный процесс") ## построение графика переходного процесса
Облик акселерометра построенного на базе вольтметра
После проектировочных расчётов данной измерительной головки видно что она в состоянии выполнять своё предназначения и измерять постоянное напряжение разных диапазонов (путём последовательного соединения с ней шунтирующих резисторов), на первый взгляд единственные её недостаток это высокая колебательность переходного процесса, чтобы избежать этих колебаний, надо в решении дифференциального уравнения колебаний рамки уменьшить влияние гармонических составляющих увеличить влияние экспонент.
Так как наш акселерометр будет строиться на базе уже рассчитанной измерительной головки вольтметра, то множество расчётов останутся прежними, самое важное отличие которое необходимо сделать это сместить центр масс рамки с её оси вращения, чтобы она могла отклоняться при возникновении линейных ускорений, так как в этом акселерометре есть обратная связь, и как следствие малые углы отклонения рамки. Так как углы отклонения малы, то угловыми ускорениями можно пренебречь
.png)
Рисунок 4 - Схема акселерометра.
1 – операционный усилитель.
2 – преобразователь напряжение – ток (резистор).
3 – резистор для получения выходного сигнала.
4 – рамка акселерометра.
5 – торсионы.
6 – два постоянных магнита.
7 – датчик угла.
Акселерометр описывается уравнением которое очень схоже с тем которое описывает измерительную головку вольтметра:
В этом уравнении левая часть полностью повторяет левую часть уравнения описывающего измерительную головку вольтметра. также в нем есть инерционный момент, который вызван разбалансом рамки (этот момент я не учитывал в расчётах, так как он мал по сравнению с остальными моментами), и момент вызванный действием ускорения на разбалансированную рамку.
Размеры рамки акселерометра
# Внутренние размеры окна рамки
a1 = 13.6*10^-3
b1 = 6.4*10^-3
# Внешние размеры окна рамки
a2 = 15*10^-3
b2 = 7.8*10^-3
# Ширина рамки:
c2 = 4*10^-3
# Ширина бортика у рамки:
t = 0.2*10^-3
# Высота бортика у рамки:
h = 0.7*10^-3
# Максимальный угол отклонения рамки:
alpha_max = 0.05
# Расстояние от оси вращения рамки до рабочего участка катушки:
R1 = 10*10^-3
#Максимальное ускорение, которое способен измерять данный акселерометр:
g_max = 100
Расчет геометрических параметров рамки акселерометра
#Средние размеры рамки акселерометра:
a3 = (a1+a2)/2
b3 = (b1+b2)/2
# Периметр и площадь рамки акселерометра:
R = a3*2+b3*2
S = a3*b3
# Площадь сечения рамки акселерометра:
s = c2*h-(c2-t*2)*(h-t)
# Объём применяемого в каркасе рамки акселерометра алюминия:
V = s*R
# Радиус провода намотанного в катушке:
r = 0.025*10^-3
Расчет электрических параметров акселерометра
#Индукция магнита:
B = 0.8
# Амплитудное напряжение датчика угла:
Ud = 0.01
# Коэффициент усиления операционного усилителя:
K3 = 1000
Ky = 1000
# Плотность тока в катушке:
ji = 5
# Коэффициент заполнения при намотке привода катушки акселерометра:
p = 0.7
# Количество слоёв провода в катушке:
n = 1
# Зная ширину рамки и радиус провода, вычисляю количество витков провода в одном слое:
k = floor((c2-2*t)/(2*r))
# Далее посчитаю количество витков в катушке:
W = k*n
# Максимальный ток в катушке акселерометра:
I_max = pi*(r*1000)^2*ji
# Электрическое сопротивление катушки акселерометра:
Rm = (ro_m*W*R)/(pi*(r*1000)^2)
# Электрическое сопротивление каркаса рамки
Ral = R*ro_al/(s*10^6)
# Коэффициент электрического демпфирования при угловом движении рамки:
Kd = (B^2*b1^2*R1^2)/Ral
Масса подвижных частей акселерометра
#Объём применяемой в катушке меди:
V2 = pi*r^2*R*W
# Масса каркаса рамки акселерометра:
m1 = ro1*V
# Масса медного провода в катушке:
m2 = ro2*V2
# Для вычисления момента инерции рамки относительно её оси вращения разобью рамку
# на 4 балки и посчитаю их массу, параллельные балки равны по длине и по массе.
#Масса короткой балки:
m3 = (m1*b3)/R
# Масса длинной балки:
m4 = (m1*a3)/R
Моменты инерции подвижных частей акселерометра
# Момент инерции длинных балок:
j1 = (2*m4*a3^2)/12
# Момент инерции коротких балок:
j2 = 2*m3*(a3/2)^2
# Момент инерции, вызванный разбалансом рамки, данный момент инерции вычисляется по теореме Штейнера.
jh = (m1+m2)*(2.5*10^-3)^2
# Суммарный момент инерции рамки с катушкой:
j3 = j1+j2+jh
Коэффициенты передаточной функции акселерометра
# Угловая жесткость пружин в подвесе:
C = (B*b1*W*I_max-j3*g_max/R1)/alpha_max
# Собственная частота колебаний измерительной головки вольтметра:
w0 = sqrt(C/j3)
f0 = w0/(2*pi)
# Коэффициент передачи:
K1 = 1/C
# Безразмерный коэффициент демпфирования:
ksi = Kd/(2*sqrt(j3*C))
# Постоянная времени:
T1 = 1/w0
# Коэффициент преобразователя угла отклонения рамки в напряжение:
K2 = Ud/alpha_max
# Коэффициент преобразования напряжение – ток.
R_out = 50
K4 = 1/(Rm+R_out)
# Коэффициент передачи обратной связи
K6 = B*b1*R1
Koc = K6
# Электрическая жесткость акселерометра:
Ce = K2*K3*K4*K6
# Передаточная функция акселерометра без учета обратной связи:
W1 = tf(1,[j3, Kd, C])*K2*K3*K4
# Передаточная функция акселерометра с учетом обратной связи
Woc = feedback(W1,Koc)
Переходный процесс акселерометра
y, t = step(Woc,0:0.0001:0.1) # расчет переходного процесса
t = collect(0:0.0001:0.1)
plot(t,y',title="Переходный процесс") ## построение графика переходного процесса
Частотная характеристика акселерометра
bodeplot(Woc) # построение графика частотной характеристики
Годограф Найквиста для акселерометра
nyquistplot(Woc) # годограф найквиста
В результате работы над статьёй проведен расчет механического акселерометра который построен на базе электромеханической измерительной головки, акселерометр обладает высокой чувствительностью (порядка 10^2) и резонансной частотой 544 Гц.