День 5 Летней школы Julia
Работа с ControlSystems.jl
Создание систем
Для работы с системами управления на Julia мы будем пользоваться пакетом ControlSystems.jl. Если у вас в вашем пространстве Engee не был установлен этот пакет, то установить его можно с помощью пакетного менеджера Pkgи функции Pkg.add. Затем подключите пакет используя using.
import Pkg; Pkg.add("ControlSystems")
using ControlSystems
Передаточная функция (ПФ)
В функцию tf мы передаем вектора, которые содержат коэффициенты многочленов числителя и знаменателя. В данном случае в числителе многочлен 0-го порядка, то есть в степени 0. В знаменателе многочлен 1-го порядка, тут в степени 1.
tf([1], [1, 2]) # коэффициенты числителя и знаменателя
Задать передаточную функцию можно используя переменную Лапласа.
s = tf("s") # переменная Лапласа
P = (s + 0.5) / (s^2 + 2s + 1)
Создадим передаточную функцию с помощью еще одной стандартной функции пакета pid().
C = pid(1,2)
Если у нас уже есть система, которая описана некоторой передаточной функцией и нам нужно узнать числитель или знаменатель. Мы можем использовать функцию numvec() для числителя и denvec() для знаменателя. Эти функции возвращают матрицу векторов, поскольку системы зачастую могут иметь несколько входов и выходов. Чтобы получить доступ к вектору коэффициентов нашей передаточной функции используем такую запись: numvec(P)[1].
numvec(P) # коэффициенты числителя ПФ
denvec(P) # коэффициенты знаменателя ПФ
Для получения фактического представления многочлена числителя передаточной функции используем функцию numpoly(P). Она возвращает матрицу многочленов. Однако члены здесь представлены в обратном порядке. Сначала идет член с меньшим порядком, затем с большим.
numpoly(P)
Операции и структурные предобразования
Мы также можем умножать передаточную функцию на скаляр.
2P # умножение на скаляр
И получать обратное значение, используя специальную функцию inv или запись 1/P.
inv(P) # обратная функция
Для структурных преобразований можно использовать стандартные функции пакета или использовать операторы “+” и “*”. Выражение P + C реализует параллельное подключение моделей. А P*C - последовательное подключение передаточных функций.
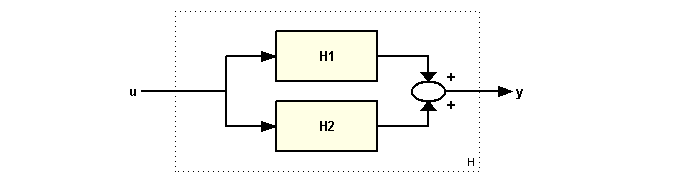
P + C # подключение моделей в параллельной форме
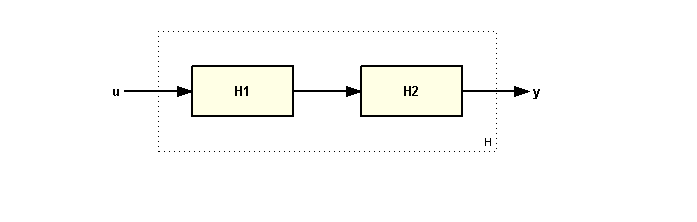
P * C # подключение моделей в последовательной форме
Для получения системы с обратной связью в пакете есть функция feedback(). Однако можно использовать формулу для замкнутой системы. Но в результате мы не получим минимальной реализации и вычисляться такое выражение будет дольше.
G1 = P*C / (1 + P*C) # создание соединиения обратной связи с использованием "/"
Получить минимальную реализацию из G1 можно используя функции: minreal и sminreal.
minreal(G1) # Получим структурно минимальную реализацию функции G1
G2 = feedback(P*C) # также реализует модель с обратной связью; рекомендуемый способ образование замкнутого контура
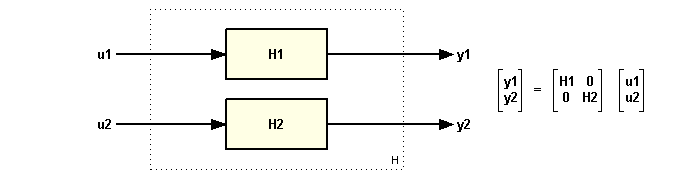
Если объединить две системы, используя вертикальную конкатенацию [P; C], будет создана MIMO система с двумя выходами. Если объединить системы горизонтально, то получится MIMO система с двумя входами. И если объединим системы по вертикали и по горизонтали, то получим систему с двумя входами и двумя выходами.
[P; C] # конкатенация моделей; создание MIMO системы
Результирующая модель имеет два выхода и один вход и соответствует следующей блок-схеме:
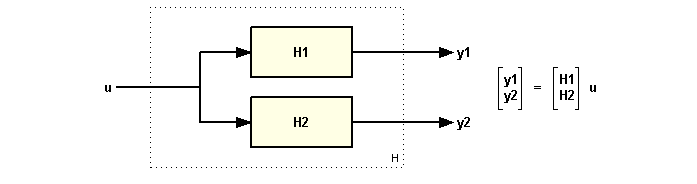
[P C]
Результирующая модель имеет два входа и один выход, что соответствует следующей схеме:
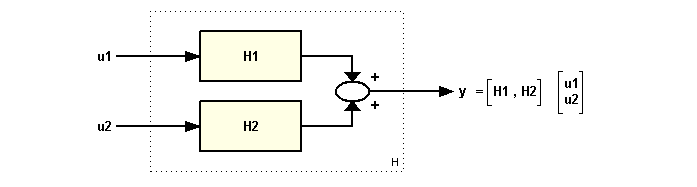
[P C; P C]
Результирующая модель имеет два входа и два выхода и соответствует структурной схеме:
Пространство состояний
Перейдем к следующему способу создания систем - описание в пространстве состояний.
Мы можем конвертировать нашу передаточную функцию в объект пространства состояний. Для этого передадим передаточную функцию P в функцию ss(). Таким образом мы получаем объект StateSpace.
P = ss(P) # конвертация в вид пространства состояний
Создать новую систему можно используя матрицы A, B, C, D, описывающие состояния нашей системы.
A = [0 1; -1 -2]
B = [0; 1]
C = [1 0]
D = 0
P = ss(A,B,C,D) # описание пространства состояний с помощью матриц
Работать с такой системой можно так же, как с передаточными функциями.
Конструктор ss позволяет делать следующее:
-
передавать 0 вместо матрицы ; нулевая матрица соответствующего размера создается автоматически;
-
передавать I вместо матрицы ; матрица тождественности соответствующего размера создается автоматически. Оператор I UniformScaling предоставляется стандартной библиотекой LinearAlgebra, которую нужно предварительно загрузить.
import Pkg; Pkg.add("LinearAlgebra")
using LinearAlgebra
P = ss(A,B,I,D)
Получить доступ к любой из матриц, то это можно сделать через точку.
P.A # доступ к матрице А
(; A, B, C, D) = P # деструктуризация системы по матрицам
Аналогично мы можем узнать число состояний, входов и выходов системы. Например, обращаясь P.nx мы получим число входов.
P.nx # число состояний
P.nu # число входов
P.ny # число выходов
Дискретные системы
Ts = 0.1;
Pd1 = tf([1], [1, 2], Ts)
Pd2 = ss(A, B, C, D, Ts) # получение дискретной системы из матриц с периодом дискретизации Ts
Функция c2d() позволяет создать из непрерывной системы дискретную. В качестве аргументов передаем непрерывную систему и период дискретизации.
C = pid(1, 2)
Cd = c2d(C, 0.1) # конвертация непрерывной ПФ в дискретную
Cd.Ts # доступ к периоду дискретизации
В конце этого раздела приведены несколько функций, для определения свойств системы. Например, можно узнать:
- дискретна ли эта система?
- устойчива ли она?
isdiscrete(Cd) # проверка: дискретная ли система
isstable(Cd) # проверка: система устойчива
Ссылки на дополнительные материалы
Создание дискретных моделей
Создание непрерывных моделей
Подключение моделей
Анализ систем
При проектировании систем управления нам важно анализировать систему. Начнем с временных характеристик.
Во временной области
sys = tf([8, 18, 32],[1, 6, 14, 24])
В библиотеке ControlSystems.jl есть функции для построения откликов на стандартные входные сигналы. Например, такие как step() - ступенчатое воздействие и impulse() - импульсное воздействие. Эти функции возвращают экземпляр SimResult. Далее его можно использовать, чтобы построить переходную и импульсную характеристики.
step(sys, 10)
impulse(sys, 10)
using Plots
plot(
plot(step(sys, 10), title="Реакция на ступенчатое воздействие"),
plot(impulse(sys, 10), title="Реакция на импульс"),
layout=(2,1)
)
Получить реакцию на произвольное входное воздействие можно с помощью lsim(). Она принимает на вход передаточную функцию или описание системы в виде пространства состояний, входное воздействие (которое может быть массивом или функцией) и время.
A = [-0.8 3.6 -2.1;-3 -1.2 4.8;3 -4.3 -1.1];
B = [0; -1.1; -0.2];
C = [1.2 0 0.6];
D = -0.6;
G = ss(A,B,C,D)
t1 = 0:0.001:18;
u1 = zeros(1,length(t1))
x_0 = [-1.0; 0.0; 2.0]
plot(lsim(G, u1, t1, x0 = x_0))
Получить характеристики переходного процесса можно с помощью stepinfo(). На вход функция принимает объект SimResult, а на выход возвращает список параметров, которые помогают оценить перерегулирование системы, время установившегося процесса и тд. Эти данные можно отобразить и на графике, используя функцию plot().
h = stepinfo(step(sys, 10))
plot(h)
В частотной области
Анализ в частотной области является ключом к пониманию устойчивости и эксплуатационных характеристик систем управления.
Получить амплитудную и фазовую характеристики системы можно используя функцию bode(). А функция margin() возвращает запасы по амплитуде и по фазе, а также значения частот для них. Полученные данные можно отразить на графике используя встроенные функции bodeplot(), marginplot().
bode(sys)
margin(sys)
bodeplot(sys, label="sys",title="Диаграмма Боде")
marginplot(sys)
Функции nicholsplot() и nyquistplot() также помогут определить устойчивость системы. Отображение графиков можно настраивать. Так, например, на диаграмму Найквиста можно добавить единичную окружность, критическую точку (-1).
nyquistplot(
sys,
unit_circle = true,
Mt_circles = false,
hz = true,
label="sys",
title="Диаграмма Найквиста"
)
nicholsplot(sys, sat = 0, val = 1)
xlims!(-180, 180)
Чтобы оценить устойчивость системы, полезно знать ее расположение полюсов и нулей. Значение полюсов и нулей можно получить с помощью функции zpkdata().
G = -(2s+1)/(s^2+3s+2);
k = 0.7;
T = feedback(G*k,1);
zpkdata(T)
Отразить графически их нахождение на плоскости можно используя pzmap(). Полюса отмечены крестиками, а нули кружочками.
G = -(2s+1)/(s^2+3s+2);
k = 0.7;
T = feedback(G*k,1);
pzmap(T; hz = true)
Для того, чтобы лучше понять, как усиление замкнутого контура влияет на устойчивость, можно построить корневой годограф. Используем встроенную функцию rlocusplot().
plot(rlocus(G,3))
Ссылки на дополнительные материалы
Расположение полюсов и нулей
Влияние значения коэффициента усиления на запас устойчивости
Частотная характеристика MIMO системы