Адаптивная фильтрация
Адаптивная фильтрация сигналов с использованием алгоритма LMS в Engee
Адаптивная фильтрация — это мощный инструмент цифровой обработки сигналов, который позволяет автоматически подстраивать параметры фильтра в соответствии с изменяющимися характеристиками входного сигнала или окружающей среды. В отличие от статических фильтров с фиксированными коэффициентами, адаптивные фильтры изменяют свои параметры в реальном времени для достижения оптимальных характеристик.
Алгоритм наименьших средних квадратов (LMS) — один из наиболее популярных алгоритмов адаптивной фильтрации благодаря своей простоте реализации и вычислительной эффективности. В этой статье мы рассмотрим практическую реализацию LMS-фильтра в Engee с использованием пакета EngeeDSP.
Принцип работы адаптивного фильтра
Адаптивный фильтр состоит из двух основных компонентов:
- Цифровой фильтр (обычно FIR-типа)
- Адаптивный алгоритм для обновления коэффициентов фильтра
Алгоритм LMS минимизирует средний квадрат ошибки между желаемым сигналом и выходом фильтра. Основное уравнение обновления весов:
w(n+1) = w(n) + μ·e(n)·x(n)
где:
- w(n) — вектор весов фильтра на шаге n
- μ — шаг адаптации (определяет скорость и стабильность сходимости)
- e(n) — ошибка (разница между желаемым и фактическим выходом)
- x(n) — вектор входных отсчетов
Ключевые параметры LMS-алгоритма
- Длина фильтра: определяет количество коэффициентов и, следовательно, сложность модели
- Шаг адаптации (μ): влияет на скорость сходимости и устойчивость
- Коэффициент утечки: предотвращает неограниченный рост коэффициентов
Теперь когда мы разобрались с теоретической составляющей этой демонстрации, рассмотрим наш пример реализации LMS-фильтра в Engee и начнём с подключения библиотек и инициализации фильтра.
Pkg.add("DSP")
using EngeeDSP, DSP
Fs = 44100 # Частота дискретизации
x = 0.05 * randn(1024*10) # Входной сигнал (белый шум)
d = filt(FIRFilter([0.5, -0.3, 0.2, 0.1, -0.05]), x) # Желаемый сигнал
HA = EngeeDSP.LMSFilter(
Algorithm = "LMS",
FilterLength = 32,
StepSize = 0.1,
LeakageFactor = 1.0,
InitialValueOfFilterWeights = 0,
AdaptPort = false,
ResetPort = "None",
OutputFilterWeights = true
)
Блок кода представленный ниже, выполняет:
-
Разделение сигнала на кадры по 500 отсчетов
-
Последовательную обработку каждого кадра с обновлением весов фильтра
-
Визуализацию изменения весов в виде анимированной гифки
# Обработка сигнала по кадрам
frameSize = 500
num_frames = length(x) ÷ frameSize
setup!(HA, x[1:frameSize], d[1:frameSize])
# Создание анимации изменения весов
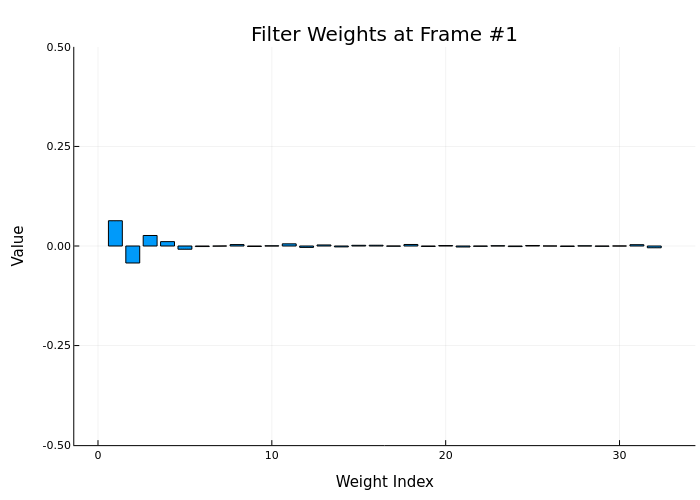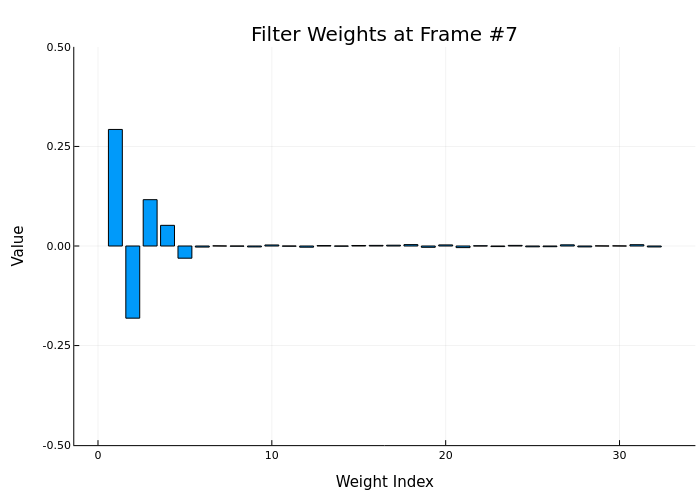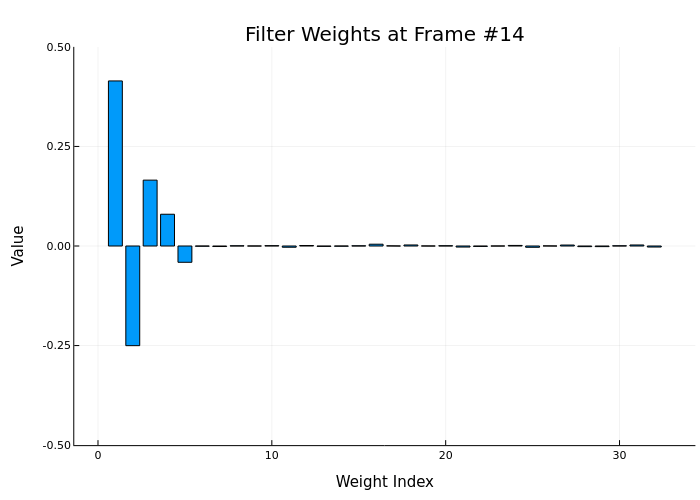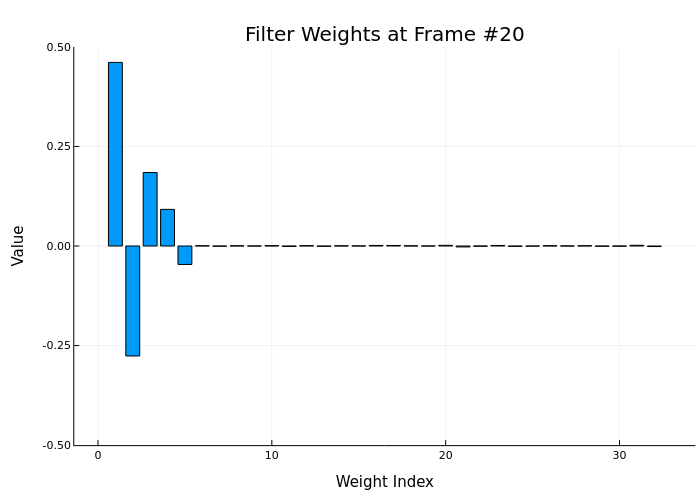
anim = @animate for i in 1:num_frames
start_idx = (i-1)*frameSize + 1
end_idx = i*frameSize
y_frame, e_frame, w = step!(HA, x[start_idx:end_idx], d[start_idx:end_idx])
bar(w, title="Filter Weights at Frame #$i",
ylims=(-0.5, 0.5), legend=false,
xlabel="Weight Index", ylabel="Value")
end
gif(anim, "weights_animation.gif", fps=5)
Заключение
Представленная реализация LMS-фильтра в Engee демонстрирует мощь и гибкость языка для задач цифровой обработки сигналов. Пакет EngeeDSP предоставляет удобный интерфейс для работы с адаптивными фильтрами, а встроенные средства визуализации позволяют легко анализировать результаты.
Ключевые преимущества этого подхода:
- Простота реализации: сложные математические алгоритмы инкапсулированы в готовые функции
- Производительность: Engee обеспечивает скорость, сравнимую с C, при удобном высокоуровневом синтаксисе
- Визуализация: возможность создания наглядных анимаций процесса адаптации
Адаптивная фильтрация находит применение во многих областях:
- Подавление шумов и эхо в аудиосистемах
- Выделение полезных сигналов на фоне помех
- Прогнозирование временных рядов
- Идентификация систем
Дальнейшее развитие этого примера может включать:
- Сравнение с другими алгоритмами (NLMS, RLS)
- Анализ влияния параметров на сходимость
- Применение к реальным сигналам (аудио, биомедицинские данные и др.)