Адаптивное управление системой первого порядка с косвенной модельной привязкой

В этом примере показано, как разработать систему адаптивного управления с косвенным заданием модели (MRAC) для слежения за эталонной моделью. Модель представляет собой неизвестную систему первого порядка. Косвенный регулятор MRAC оценивает параметры модели и реализует регулятор на основе инверсии для отслеживания эталонной модели.

Неизвестная модель реального объекта первого порядка

Управляемый реальный объект представляет собой следующую динамическую систему первого порядка:

$$\dot{x} = a x(t) + b u(t),$$

где:

• $x$ - состояние системы;
• $a$ и $b$ - неизвестные параметры системы.

Учитывая эту неизвестную нелинейную систему, задача состоит в том, чтобы разработать контроллер, позволяющий отслеживать следующую эталонную модель:

$$\dot{x}_m = a_m x_m(t) + b_mr(t),$$

где:

• $x_m$ - эталонное состояние системы;
• $r(t)$ - опорный сигнал, предоставляемый пользователем;
• $a_m$ и $b_m$ - эталонные параметры модели.

Контроллер для отслеживания эталонного сигнала

Косвенный контроллер MRAC использует оценочную модель для вычисления $\hat{a}$ и $\hat{b}$, которые являются оценками неизвестных параметров системы $a$ и $b$, соответственно:

$$\dot{\hat{x}} = \hat{a} x(t) + \hat{b} u(t).$$

Для вычисления управляющего воздействия $u(t)$ контроллер использует коэффициент усиления с прямой связью $k_r$ и коэффициент усиления $k_x$ с обратной связью:

$$u(t) = -k_x x(t) + k_r r(t).$$

Значения коэффициента полезного действия контроллера рассчитываются на основе параметров эталонной модели ($a_m$ и $b_m$) и расчетных параметров наблюдателя ($\hat{a}$ и $\hat{b}$).

$$k_r = \frac{b_m}{\hat{b}};$$ $$k_x = \frac{1}{\hat{b}}(a_m - \hat{a}).$$

Настройки контроллера

Для этого примера истинная эталонная модель выглядит следующим образом:

$$\dot{x} = x(t) + 3 u(t).$$

Укажите параметры эталонной модели, предполагая, что выходные данные модели соответствуют состоянию $x$:

a = 1.0;
b = 3.0;
c = 1.0;
d = 0.0;

Эта истинная модель неизвестна косвенному контроллеру MRAC. Вместо этого контроллер использует оценочную модель для оценки неизвестной модели динамики установки. Во время работы контроллер адаптирует параметры этой модели для улучшения оценки неизвестных параметров системы.

Укажите начальные параметры оценки:

ahat = 0.0;
bhat = 1.0;

Целью контроллера является повторение выходных параметров эталонной модели. Укажите параметры эталонной модели:

am = -4.0;
bm = 4.0;

Укажите исходное состояние устройства:

x_0 = 0.0;

Укажите скорость обучения для обновления параметров оценочной модели:

gamma_A = 2.0;  # ahat learning rate
gamma_B = 2.0;  # bhat learning rate

Запуск симуляции

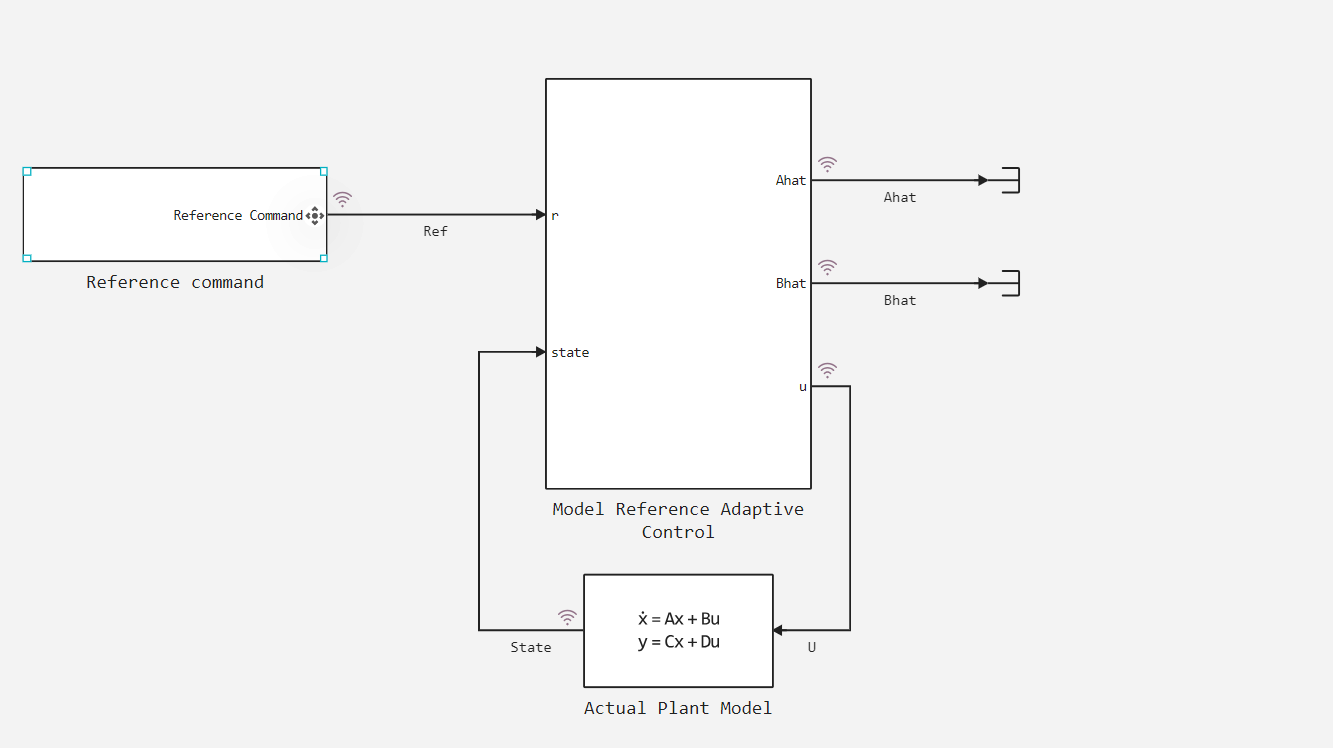
В данной модели:

• Блок Actual Plant Model реализует номинальную модель неизвестной системы первого порядка;
• Блок Reference command генерирует опорный сигнал;
• Блок Model Reference Adaptive Control выдает управляющее воздействие u, которое он получает на основе использования модели оценщика.

Хотя контроллер MRAC также может оценивать неизвестные возмущения в управляемой системе, в данном примере таких возмущений нет. Вместо этого целью контроллера является простая оценка параметров неизвестной модели установки.

# Загрузим модель, если она еще не открыта на холсте
if "MRAC" ∉ getfield.(engee.get_all_models(), :name)
    engee.load( "$(@__DIR__)/MRAC.engee");
end

model_data = engee.run( "MRAC" );

Построение графиков

Просмотрите фактический выходной сигнал устройства и опорный сигнал. Контроллер может точно отслеживать фактическое состояние устройства в соответствии с опорным сигналом.

model_data = engee.run( "MRAC" );

State = model_data["State"].value
Reference = model_data["Ref"].value

plot( model_data["Ref"].time, Reference, xlabel="Время, с", label="Reference", lw=2 )
plot!( model_data["State"].time, State, xlabel="Время, с", label="State", lw=2 )

Блок MRAC сконфигурирован для вывода параметров $\hat{a}$ и $\hat{b}$ оценочной модели с использованием выходных портов Hat и Bhat, соответственно.

Ahat = model_data["Ahat"].value
Bhat = model_data["Bhat"].value

plot( model_data["Ahat"].time, Ahat, xlabel="Время, с", label="Ahat", lw=2 )
plot!( model_data["Bhat"].time, Bhat, xlabel="Время, с", label="Bhat", lw=2 )

Вывод

Каждый шаг контроллер корректирует значения параметров оценщика. При достаточной продолжительности возмущения в опорном сигнале, $\hat{a}$ и $\hat{b}$ сходятся к своим истинным значениям 1 и 3, соответственно.