Анализ модуляций
Анализ модуляционных схем
В данном исследовании представлен системный подход к реализации и верификации тестовых моделей приёмо-передающих трактов в среде Engee. Работа включает последовательный анализ различных аспектов модуляционных схем, начиная с базовых характеристик и заканчивая спектральными свойствами.
Вспомогательная функция управления моделями
Для обеспечения корректной работы с моделями реализована функция run_model, которая автоматизирует процесс загрузки и выполнения моделей. Функция выполняет следующие операции:
-
Формирует полный путь к файлу модели с расширением
.engee -
Проверяет текущее состояние модели в ядре системы
-
При необходимости загружает модель из файла или открывает уже загруженную
-
Выполняет запуск модели с выводом подробной информации о процессе
-
Обеспечивает корректное завершение работы с моделью
-
Возвращает результаты выполнения
Данный подход гарантирует стабильную работу независимо от начального состояния системы.
function run_model( name_model)
Path = (@__DIR__) * "/" * name_model * ".engee"
if name_model in [m.name for m in engee.get_all_models()]
model = engee.open( name_model )
model_output = engee.run( model, verbose=true );
else
model = engee.load( Path, force=true )
model_output = engee.run( model, verbose=true );
engee.close( name_model, force=true );
end
sleep(0.1)
return model_output
end
Анализ вероятности битовой ошибки
Проведено сравнительное исследование характеристик четырёх модуляционных схем: BPSK, QPSK, 8-PSK и 16-QAM. Методика исследования включает:
-
Моделирование в диапазоне отношений сигнал-шум (Eb/No) от 0 до 10 дБ с шагом 2 дБ
-
Теоретический расчёт характеристик BER с использованием математических моделей для каждой модуляции
-
Визуализацию результатов в логарифмическом масштабе для наглядного сравнения
Была использована базовая модель, содержащая идентичные тракты обработки сигнала для всех модуляций, что обеспечивает корректность сравнительного анализа, сама модель продемонстрирована ниже.
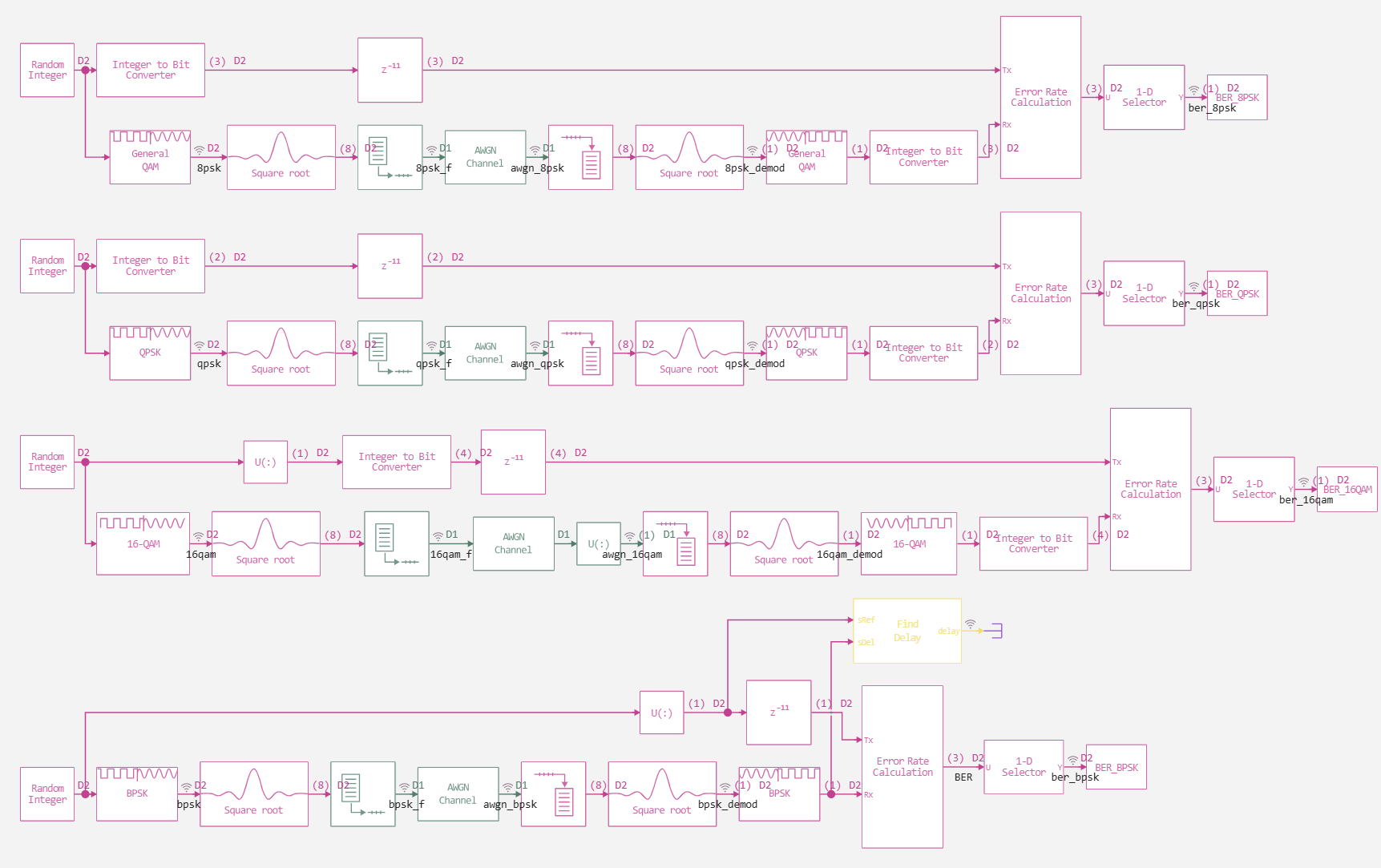
EbNoArr = collect(0:2:10);
Eb_No = 0;
ber_bpsk = zeros(length(EbNoArr));
ber_8psk = zeros(length(EbNoArr));
ber_qpsk = zeros(length(EbNoArr));
ber_16qam = zeros(length(EbNoArr));
for i in 1:length(EbNoArr)
Eb_No = EbNoArr[i]
run_model("modulations_1");
ber_bpsk[i] = collect(BER_BPSK).value[end][1]
ber_8psk[i] = collect(BER_8PSK).value[end][1]
ber_qpsk[i] = collect(BER_QPSK).value[end][1]
ber_16qam[i] = collect(BER_16QAM).value[end][1]
end
using SpecialFunctions
colors = Dict(:BPSK => :blue, :QPSK => :red, :PSK8 => :green, :QAM16 => :purple)
function theoretical_ber(EbNo_dB, mod_type)
EbNo = 10 .^ (EbNo_dB ./ 10)
if mod_type == :BPSK
0.5 .* erfc.(sqrt.(EbNo))
elseif mod_type == :QPSK
0.5 .* erfc.(sqrt.(EbNo))
elseif mod_type == :PSK8
(2/3) .* erfc.(sqrt.(3*EbNo) .* sin(π/8))
elseif mod_type == :QAM16
(3/8) .* erfc.(sqrt.(2 .* EbNo ./ 5))
end
end
EbNoArr_dense = range(minimum(EbNoArr), maximum(EbNoArr), length=1000)
plot(yscale=:log10, ylims=(1e-6, 1), grid=true, xlabel="Eb/No (dB)", ylabel="BER", title="Теоретический и смоделированный BER")
for mod in [(:BPSK, ber_bpsk), (:QPSK, ber_qpsk), (:PSK8, ber_8psk), (:QAM16, ber_16qam)]
mod_type, ber_sim = mod
c = colors[mod_type]
plot!(EbNoArr_dense, theoretical_ber(EbNoArr_dense, mod_type), line=:solid, color=c, label="$mod_type (теор.)")
scatter!(EbNoArr, ber_sim, marker=:circle, color=c, label="$mod_type (симул.)", markersize=5)
end
plot!(legend=:bottom)
Анализ мощностных характеристик и сигнальных созвездий
Исследование расширено за счёт модели с фильтрами Найквиста в приёмо-передающих трактах. Проведён анализ:
-
Мощности сигналов до и после фильтрации для оценки влияния фильтров
-
Сигнальных созвездий демодулированных сигналов для визуальной оценки качества демодуляции
Построены созвездия для всех рассматриваемых модуляционных схем с отображением эталонных точек.
Сама модель представлена ниже.
.png)
run_model("modulations_2")
using Statistics
println("До фильтра:")
bpsk = collect(simout["modulations_2/bpsk"]).value
power_bpsk = mean(abs2.(x[1]) for x in bpsk)
println("Мощность BPSK: $power_bpsk")
qpsk = collect(simout["modulations_2/qpsk"]).value
power_qpsk = mean(abs2.(x[1]) for x in qpsk)
println("Мощность QPSK: $power_qpsk")
psk8 = collect(simout["modulations_2/8psk"]).value
power_8psk = mean(abs2.(x[1]) for x in psk8)
println("Мощность 8PSK: $power_8psk")
qam16 = collect(simout["modulations_2/16qam"]).value
power_16qam = mean(abs2.(x[1]) for x in qam16)
println("Мощность 16QAM: $power_16qam")
println("После фильтра:")
bpsk = collect(simout["modulations_2/bpsk_f"]).value
power_bpsk = mean(abs2.(x[1]) for x in bpsk)
println("Мощность BPSK: $power_bpsk")
qpsk = collect(simout["modulations_2/qpsk_f"]).value
power_qpsk = mean(abs2.(x[1]) for x in qpsk)
println("Мощность QPSK: $power_qpsk")
psk8 = collect(simout["modulations_2/8psk_f"]).value
power_8psk = mean(abs2.(x[1]) for x in psk8)
println("Мощность 8PSK: $power_8psk")
qam16 = collect(simout["modulations_2/16qam_f"]).value
power_16qam = mean(abs2.(x[1]) for x in qam16)
println("Мощность 16QAM: $power_16qam")
Выполним построения созведия для каждой из модуляций.
bpsk = collect(simout["modulations_2/bpsk_demod"]).value
bpsk = [x[1] for x in bpsk] # Извлекаем первый элемент каждого вектора
plot(title="BPSK")
plot!(bpsk, seriestype=:scatter)
plot!([-1+0im, 1+0im], seriestype=:scatter)
qpsk = collect(simout["modulations_2/qpsk_demod"]).value;
qpsk = [x[1] for x in qpsk] # Извлекаем первый элемент каждого вектора
plot(title="QPSK")
plot!(ComplexF64.(qpsk), seriestype=:scatter)
plot!([0.75+0.75im, 0.75-0.75im, -0.75+0.75im, -0.75-0.75im], seriestype=:scatter)
psk8 = collect(simout["modulations_2/8psk_demod"]).value;
psk8 = [x[1] for x in psk8] # Извлекаем первый элемент каждого вектора
plot(title="8-PSK")
plot!(ComplexF64.(psk8), seriestype=:scatter)
plot!(cis.(2pi*[0:7...]/8), seriestype=:scatter)
qam16 = collect(simout["modulations_2/16qam_demod"]).value;
qam16 = [(i...)+0 for i in qam16];
plot(title="16QAM")
plot!(ComplexF64.(qam16), seriestype=:scatter)
plot!([a + b*im for a in -3:2:3, b in -3:2:3][:], seriestype=:scatter)
Спектральный анализ модулированных сигналов
Для углублённого исследования свойств модулированных сигналов выполнено:
-
Расчёт спектральной плотности мощности с применением:
-
Оконной функции Хэннинга для уменьшения эффектов спектральной утечки
-
Медианной фильтрации для сглаживания спектральных характеристик
-
-
Сравнение с теоретической моделью спектра Найквиста с коэффициентом сглаживания 0.2
-
Визуализацию спектральных характеристик в частотной области
Реализованная модель демонстрирует возможности анализа многочастотных систем с использованием буферизации данных.
.png)
using FFTW, DSP, Statistics, SpecialFunctions
function compute_smoothed_spectrum(signal, fs, window_size=20)
window = hanning(length(signal))
windowed_signal = signal .* window
power_spectrum = abs.(fft(windowed_signal)).^2 / (sum(abs2, window) * fs)
power_spectrum_db = 10*log10.(power_spectrum)
function my_medfilt(signal, window_size)
half_window = window_size ÷ 2
smoothed = similar(signal)
n = length(signal)
for i in 1:n
start_idx = max(1, i - half_window)
end_idx = min(n, i + half_window)
window_data = signal[start_idx:end_idx]
smoothed[i] = median(window_data)
end
return smoothed
end
power_spectrum_db_smoothed = my_medfilt(power_spectrum_db, window_size)
freqs = fftfreq(length(signal), fs)
return fftshift(freqs), fftshift(power_spectrum_db_smoothed)
end
function nyquist_spectrum(frequencies, rolloff_factor=0.5, symbol_rate=1.0)
T = 1.0 / symbol_rate
f_N = 1.0 / (2 * T)
spectrum = zeros(length(frequencies))
for (i, f) in enumerate(frequencies)
f_abs = abs(f)
if f_abs <= (1 - rolloff_factor) * f_N
spectrum[i] = T
elseif f_abs <= (1 + rolloff_factor) * f_N && f_abs > (1 - rolloff_factor) * f_N
spectrum[i] = T/2 * (1 + cos(π * T / rolloff_factor * (f_abs - (1 - rolloff_factor) * f_N)))
else
spectrum[i] = 0.0
end
end
spectrum_db = 10 * log10.(spectrum .+ 1e-12)
return spectrum_db
end
fs = 400
window_size = 15
symbol_rate = 50.0
rolloff = 0.2
run_model("modulations_3")
bpsk = collect(simout["modulations_3/bpsk_f"]).value
bpsk = [(i...)+0 for i in bpsk]
qpsk = collect(simout["modulations_3/qpsk_f"]).value
qpsk = [(i...)+0 for i in qpsk]
psk8 = collect(simout["modulations_3/8psk_f"]).value
psk8 = [(i...)+0 for i in psk8]
qam16 = collect(simout["modulations_3/16qam_f"]).value
qam16 = [(i...)+0 for i in qam16]
freqs_bpsk, spectrum_bpsk = compute_smoothed_spectrum(bpsk, fs, window_size)
freqs_qpsk, spectrum_qpsk = compute_smoothed_spectrum(qpsk, fs, window_size)
freqs_psk8, spectrum_psk8 = compute_smoothed_spectrum(psk8, fs, window_size)
freqs_qam16, spectrum_qam16 = compute_smoothed_spectrum(qam16, fs, window_size)
freqs_theoretical = range(-fs/2, fs/2, length=1000)
spectrum_nyquist_02 = nyquist_spectrum(freqs_theoretical, 0.2, symbol_rate)
max_experimental = maximum([maximum(spectrum_bpsk), maximum(spectrum_qpsk), maximum(spectrum_psk8), maximum(spectrum_qam16)])
max_theoretical_02 = maximum(spectrum_nyquist_02)
spectrum_nyquist_02_normalized = spectrum_nyquist_02 .- (max_theoretical_02 - max_experimental)
plot(freqs_bpsk, spectrum_bpsk, label="BPSK", linewidth=2, grid=true)
plot!(freqs_qpsk, spectrum_qpsk, label="QPSK", linewidth=2)
plot!(freqs_psk8, spectrum_psk8, label="8-PSK", linewidth=2)
plot!(freqs_qam16, spectrum_qam16, label="16-QAM", linewidth=2)
plot!(freqs_theoretical, spectrum_nyquist_02_normalized, label="Найквист α=0.2", linewidth=3, linestyle=:dash, color=:red)
title!("Энергетический спектр модулированных сигналов (fs = $fs Гц)\nМедианный фильтр с окном $window_size")
xlabel!("Частота, Гц")
ylabel!("Спектральная плотность мощности, дБ/Гц")
xlims!(-fs/2, fs/2)
Полученные результаты позволяют провести комплексный анализ модуляционных схем и обосновать выбор оптимальной модуляции для конкретных условий эксплуатации систем связи.
Вывод.
На основе комплексного анализа характеристик модуляционных схем можно сделать следующие выводы.
| Параметр | BPSK | QPSK | 8-PSK | 16-QAM |
|---|---|---|---|---|
| Эффективность | 1 б/с/Гц | 2 б/с/Гц | 3 б/с/Гц | 4 б/с/Гц |
| Требуемый Eb/No для BER=10⁻³ | ~7 дБ | ~7 дБ | ~11 дБ | ~15 дБ |
| Сложность демодуляции | Низкая | Низкая | Средняя | Высокая |
Лучший выбор для различных сценариев:
- Для максимальной помехоустойчивости → BPSK
- Оптимальный компромисс → QPSK ⭐
- При ограниченной полосе и хорошем SNR → 8-PSK
- Для максимальной скорости в идеальных условиях → 16-QAM
Подводя итог, можно сказать, что QPSK является наиболее сбалансированным и практичным выбором для большинства реальных систем связи, обеспечивая оптимальное соотношение помехоустойчивости, спектральной эффективности и простоты реализации. BPSK следует использовать в системах с экстремальными требованиями к надёжности, а более высокоуровневые модуляции - только при гарантированно хорошем качестве канала связи.