Анализ непрерывных динамических систем

1. Получение математической модели рассматриваемой системы.

Дано, настройки, подготовочный код

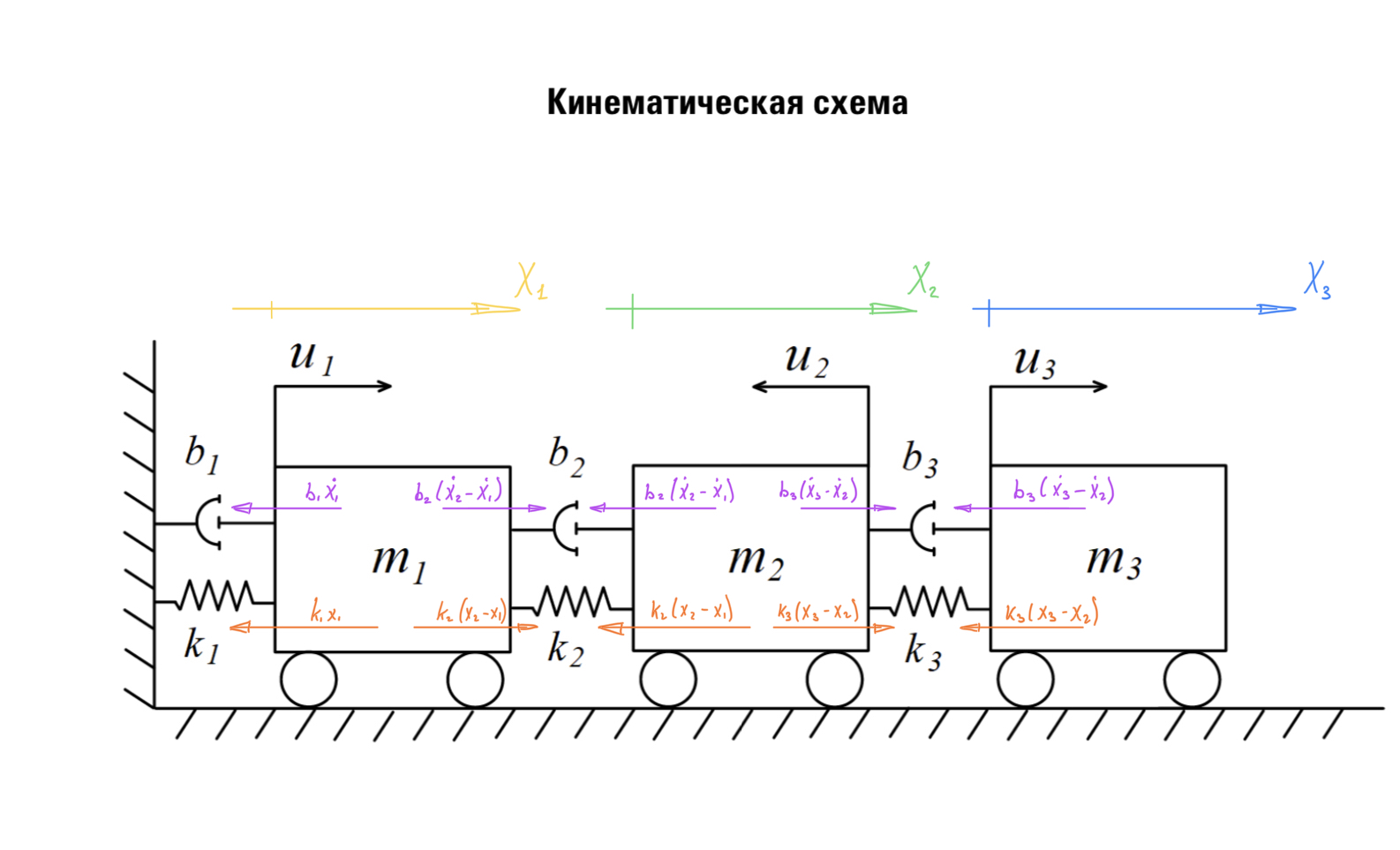
Рис. 1 Кинематическая схема

using ControlSystemsBase, SymPy, LinearAlgebra, Plots

plot_backend_func = "gr()" # @param ["gr()","plotlyjs()","pyplot()"]

eval(Meta.parse(plot_backend_func))

# Функция для определения степени полинома
function get_poly_degree(expr, s)
    degree = 0
    current_expr = expr
    while true
        derivative = diff(current_expr, s)
        derivative == 0 && break
        degree += 1
        current_expr = derivative
    end
    return degree
end

function get_coeffs(expr, s)
    n = get_poly_degree(expr, s)
    coeffs = zeros(Float64, n+1)
    for k in 0:n
        deriv = expr
        for _ in 1:k
            deriv = diff(deriv, s)
        end
        coeff = deriv.subs(s, 0) / factorial(k)
        coeffs[k+1] = Float64(coeff)
    end
    return coeffs
end

function sym_to_tf(expr, s)
    num_expr = numerator(expr)
    den_expr = denominator(expr)

    num_coeffs = get_coeffs(num_expr, s) |> reverse
    den_coeffs = get_coeffs(den_expr, s) |> reverse
    
    return tf(num_coeffs, den_coeffs)
end


function nyquist_marginplot(sys; kwargs...)
    # Вычисление запасов
    wgm, gm, wpm, pm = margin(sys)  
    GM_dB = 20*log10.(gm)

    wgm = wgm[1]
    gm = gm[1]
    wpm = wpm[1]
    pm = pm[1]
    
    # Построение годографа
    p = nyquistplot(sys; unit_circle=true, kwargs...)
    
    # Добавление точек запасов
    scatter!([-1 / gm], [0], color=:blue, label="GM = $(1 + (-1 / gm))")
    
    # Точка PM
    pm_point = exp(im * deg2rad(pm-180))
    scatter!([real(pm_point)], [imag(pm_point)], 
             color=:green, label="PM = $(round(pm,digits=2)[1])°")
    
    return p
end


function derivative_val(t, z_vect)
    M = [
        0.0     1.0     0.0     0.0     0.0     0.0;
        -2.2   -2.2     0.2     0.2     0.0     0.0;
        0.0     0.0     0.0     1.0     0.0     0.0;
        0.04   0.04   -0.08   -0.08    0.04    0.04;
        0.0     0.0     0.0     0.0     0.0     1.0;
        0.0    0.0    0.04    0.04    -0.04    -0.04
    ]
    V = [0, 1, 0, 0, 0, 0]

    return M * z_vect + V
end

function runge_kutta4(f, z0, t0, t_end, h)
    t_values = collect(t0:h:t_end)
    n = length(t_values)
    z = copy(z0)
    z_values = [z0]
    
    for i in 1:n-1
        t = t_values[i]
        k1 = h .* f(t, z)
        k2 = h .* f(t + h/2, z .+ k1./2)
        k3 = h .* f(t + h/2, z .+ k2./2)
        k4 = h .* f(t + h, z .+ k3)
        z = z .+ (k1 .+ 2 .* k2 .+ 2 .* k3 .+ k4) ./ 6
        append!(z_values, [z])
    end
    
    return t_values, z_values
end


function plot_rk4_data(x, xd, i)
    p = plot( 
        title = "Движение тела $i по rk4",
        ylabel = "x$i",
        label = "x$i",
        linewidth = 2,
        linecolor = :blue,
        t_values, 
        size = (900, 700),
        x
    )
        
    plot!(
        twinx(),
        ylabel = "x$i'",
        label = "x$i'",
        linewidth = 2,
        linecolor = :red,
        linestyle = :dash,
        t_values, 
        xd
    )
    return p
end


function calc_lfch(W, ω)
    H = freqresp(W, ω)[1, 1, :]
    amp_dB = 20*log10.(abs.(H))
    phase_deg = angle.(H) .* (180/π)
    return amp_dB, phase_deg
end


function plot_lfch(ω, amp_dB, phase_deg)
    lfch = plot(
        layout = (2,1),
        title = ["Amplitude [dB]" "Phase [°]"],
        size=(1000, 400)
    )
    plot!(lfch[1], ω, amp_dB, label="A", ylabel="dB", lw=2, color=:red, xaxis=:log10)
    plot!(lfch[2], ω, phase_deg, label="phi", ylabel="°", lw=2, color=:blue, xaxis=:log10)
    return lfch
end


function mich_plot(Ds, ω)
    values = map(x -> x[1], Ds.(ω * im))

    p = plot(real(values), imag(values), lw=2, color=:blue)
    hline!([0], line = (:black, :dash, 0.5), label = "")
    vline!([0], line = (:black, :dash, 0.5), label = "")
    title!("ω ∈ [$(ω[1]), $(ω[end])]")
    return p
end

rows(M) = [M[i,:]' for i in 1:size(M, 1)];

[ Info: Precompiling SciMLBasePyCallExt [d083c4ab-32a5-5342-b289-e118b48fb79d] (cache misses: wrong dep version loaded (2), mismatched flags (2), wrong julia version (2))
[ Info: Precompiling SymbolicsSymPyExt [f04539eb-3b94-5d9d-8be7-45665d72dc4b] (cache misses: wrong dep version loaded (2))

1.1. Получить математическое описание рассматриваемой системы в виде системы дифференциальных уравнений с использованием формализма Лагранжа.

1.2. Привести полученную систему дифференциальных уравнений к нормальной форме Коши.

1.3. Получить численное решение задачи Коши

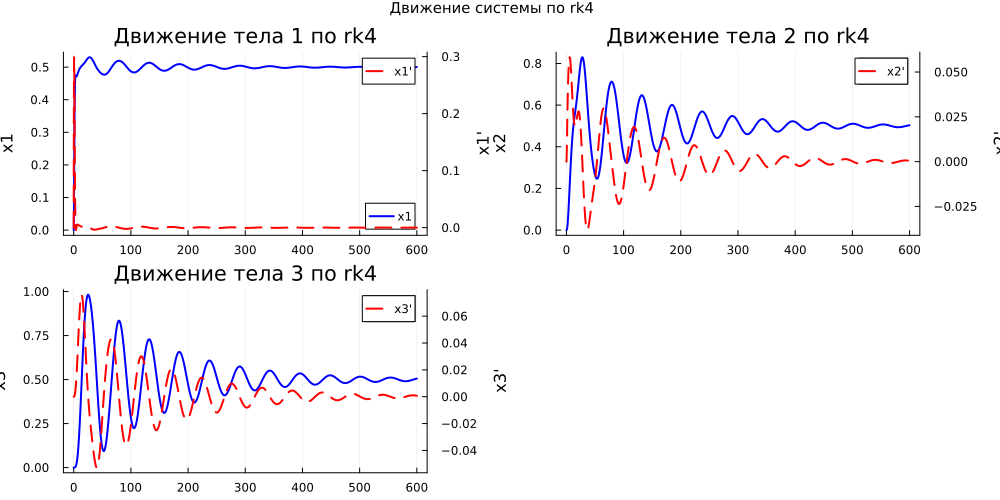
Получить численное решение задачи Коши для заданной системы с нулевыми начальными условиями, шагом моделирования h= 0.1 и длительностью моделирования T_max = 30 сек (задать соответствующий вектор–столбец времени) и одновременное действующими управлениями 1 u_i = (где i соответствует индивидуальному варианту задания) с использованием численного методу Рунге–Кутта 4-го порядка. Построить на одной фигуре три вертикально расположенных графика. На верхнем отобразить изменение x_1 и x_1' , на среднем x_2 и x_2' , а на нижнем x_3 и x_3' . При построении графиков слева отобразить ось для координаты, а справа для скорости, для чего использовать конструкцию yyaxis.

start_time = 0.0    # @param {type:"number"}
end_time = 600.0    # @param {type:"number"}
step_time = 0.1     # @param {type:"number"}


t_values, z_values = runge_kutta4(derivative_val, [0.0 for _ = 1:6], start_time, end_time, step_time)
x1 = [z[1] for z in z_values]
x1d = [z[2] for z in z_values]
x2 = [z[3] for z in z_values]
x2d = [z[4] for z in z_values]
x3 = [z[5] for z in z_values]
x3d = [z[6] for z in z_values];

# @markdown ##### Построение графика движения системы по rk4
p1 = plot_rk4_data(x1, x1d, 1)
p2 = plot_rk4_data(x2, x2d, 2)
p3 = plot_rk4_data(x3, x3d, 3)
plot(p1, p2, p3, 
    size=(1000, 500), 
    plot_title="Движение системы по rk4", 
    plot_titlefontsize=10
)

Рис. 2. Движение системы по rk4

1.5. Получить математическое описание подсистемы и заданного входного воздействия, соответствующих индивидуальному варианту задания, в виде передаточной функции.

По условию варианта нужно составить передаточные функции для тела 1

# @markdown ##### Расчет общего вида передаточной функции методом символьных вычислений
@syms s, m1, m2, m3, b1, b2, b3, k1, k2, k3

a = m1*s^2 + (b1+b2)*s + k1 + k2 
b = -(b2*s + k2)
c = m2*s^2 + (b2 + b3) * s + k2 + k3 
d = -(b3 * s + k3)
e = m3 * s^2 + b3 * s + k3

W2_obs = simplify(-a*e / (a * c * e - a * d^2 - b^2 * e));

# @markdown ##### Расчет передаточной функции с числами из варианта задания
exp_vals = Dict(m1=>1, m2=>5, m3=>5, b1=>2, b2=>0.2, b3=>0.2, k1=>2, k2=>0.2, k3=>0.2)

W2_num = simplify(W2_obs(exp_vals))
W2 = sym_to_tf(W2_num, s);

1.6. Получить математическое описание рассматриваемой системы в пространстве состояний, используя описание системы в виде дифференциальных уравнений. Для формирования уравнения выхода считать, что измеряются выходные координаты x_1 , x_2 и x_3 .

1.7. Получить каноническую форму управляемости и наблюдаемости, используя изложенный в лекциях алгоритм расчета, а не готовые программные решения.

# @markdown ###### Исходные параметры матрицы в пространстве состояний
A = [
    0.0     1.0     0.0     0.0     0.0     0.0;
    -2.2   -2.2     0.2     0.2     0.0     0.0;
    0.0     0.0     0.0     1.0     0.0     0.0;
    0.04   0.04   -0.08   -0.08    0.04    0.04;
    0.0     0.0     0.0     0.0     0.0     1.0;
    0.0    0.0    0.04    0.04    -0.04    -0.04
]
B = [
    0   0   0;
    1   0   0;
    0   0   0;
    0  -0.2 0;
    0   0   0;
    0   0   0.2]

C = [
    1 0 0 0 0 0;
    0 0 1 0 0 0;
    0 0 0 0 1 0
]

D = [0 0 0; 0 0 0; 0 0 0];

Расчет канонической формы управляемости

@syms s

I = eye(6)

char_pal_matr = s.* I - A

W = [
    0.0096  0.2672  0.5184  2.5576  2.32    1;
    0.2672  0.5184  2.5576  2.32    1       0;
    0.5184  2.5576  2.32    1       0       0;
    2.5576  2.32    1       0       0       0;
    2.32    1       0       0       0       0;
    1       0       0       0       0       0;
]
M = [B A^1*B A^2*B A^3*B A^4*B A^5*B];

Матрица M: Снимок экрана 2025-06-17 в 12.43.06.png

T = [M[i, j] for i =1:6, j in [1, 4, 2, 5, 3, 6]];

inv_T = inv(T);

# display(round.(inv_T*A*T, digits=14))
# display(round.(inv_T*B, digits=14))
# display(round.(C*T, digits=14))

Матрица T^{-1}AT имеет другой вид, т.к. это MIMO система

Расчет канонической формы наблюдаемости

M_tilda = [C[1, :]'; C[1, :]'*A; C[2, :]'; C[2, :]'*A; C[3, :]'; C[3, :]'*A]
inv_M_tilda = inv(M_tilda)

q1 = inv_M_tilda[:, 2]
q2 = inv_M_tilda[:, 4]
q3 = inv_M_tilda[:, 6]
q = q3 
T = [q1 A*q1 q2 A*q2 q3 A*q3]

inv_T = inv(T);

# display(round.(inv_T*A*T, digits=14))
# display(round.(inv_T*B, digits=14))
# display(round.(C*T, digits=14))

Матрица T^{-1}AT имеет другой вид, т.к. это MIMO система

2. Построение и исследование временных характеристик системы

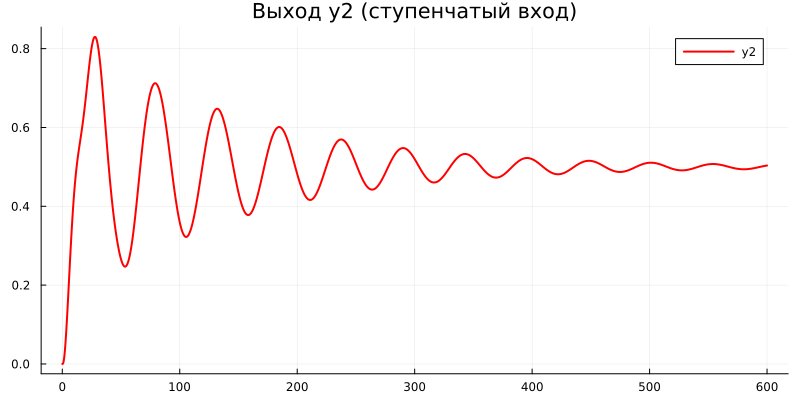
2.1. Для рассматриваемой подсистемы и заданного входного воздействия, соответствующих индивидуальному варианту задания, построить графики переходных характеристик c использованием функции `lsim()`.

Примечание. Функция lsim() требует задания дополнительного входного параметра – вектора значений входного сигнала. В рассматриваемой системе два входа. Другими словами параметр входного сигнала в функции lsim() представляет собой матрицу из 3 столбцов с количеством строк эквивалентным количеству элементов в векторе времени. Следовательно,1необходимо предварительно сформировать два вектора из единиц такой же размерности, как и вектор времени. Ввиду того, что при построении переходных характеристик рассматривается действие только одного входа, то дополнительно необходимо предварительно сформировать нулевой вектор такой же размерности, как и вектор времени. Затем для построения переходных характеристик необходимо сформировать subplot (формирование требуемого входного воздействие реализуется за счет горизонтальной конкатенации сформированных векторов).

Примечание. Заданное входное воздействие задается равным единице, а остальные нулю.

# @markdown ###### Исходные параметры матрицы в пространстве состояний
A = [
    0.0     1.0     0.0     0.0     0.0     0.0;
    -2.2   -2.2     0.2     0.2     0.0     0.0;
    0.0     0.0     0.0     1.0     0.0     0.0;
    0.04   0.04   -0.08   -0.08    0.04    0.04;
    0.0     0.0     0.0     0.0     0.0     1.0;
    0.0    0.0    0.04    0.04    -0.04    -0.04
]
B = [
    0   0   0;
    1   0   0;
    0   0   0;
    0  -0.2 0;
    0   0   0;
    0   0   0.2]

C = [
    1 0 0 0 0 0;
    0 0 1 0 0 0;
    0 0 0 0 1 0
]

D = [0 0 0; 0 0 0; 0 0 0]

sys = ss(A, B, C, D)
dx = 0.1;
t = [0:dx:600;];

# @markdown ##### Построение графика переходного процесса при ступенчатом входном воздействии

u_step = [ones(1, length(t)); zeros(1, length(t)); zeros(1, length(t))]

step_res = lsim(sys, u_step, t)

step_plot = plot(t, step_res.y[2, :], lw=2, color=:red, 
    label="y2", 
    title = "Выход y2 (ступенчатый вход)", 
    xlabel = "",
    size=(800, 400)
)

Рис. 3. График переходного процесса для ступенчатого воздействия

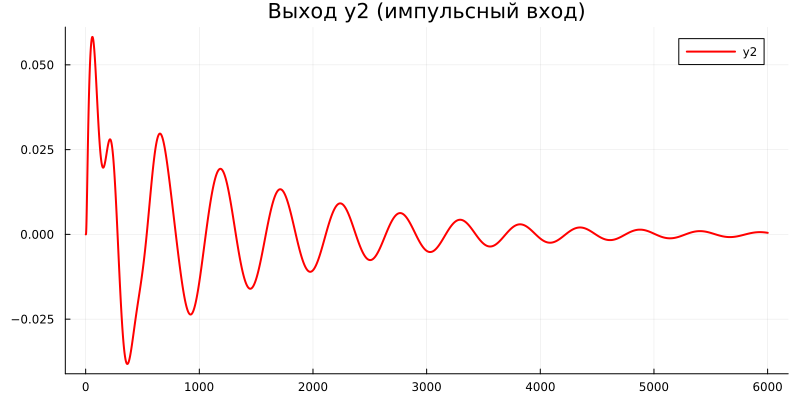
2.2. Повторить пункт задания 2.1, но для построения импульсных переходных характеристик.

# @markdown ##### Построение графика переходного процесса при импульсном входном воздействии

u_impulse = [zeros(1, length(t)); zeros(1, length(t)); zeros(1, length(t))]
u_impulse[1, 2] = 1/dx # во второй точке, чтобы быть уверенным что площать равна 1

impulse_res = lsim(sys, u_impulse, t)

plot(impulse_res.y[2, :], lw=2, color=:red, 
    label="y2",
    title = "Выход y2 (импульсный вход)",
    xlabel = "",
    size=(800, 400)
)

Рис. 4. График переходного процесса для импульсного воздействия

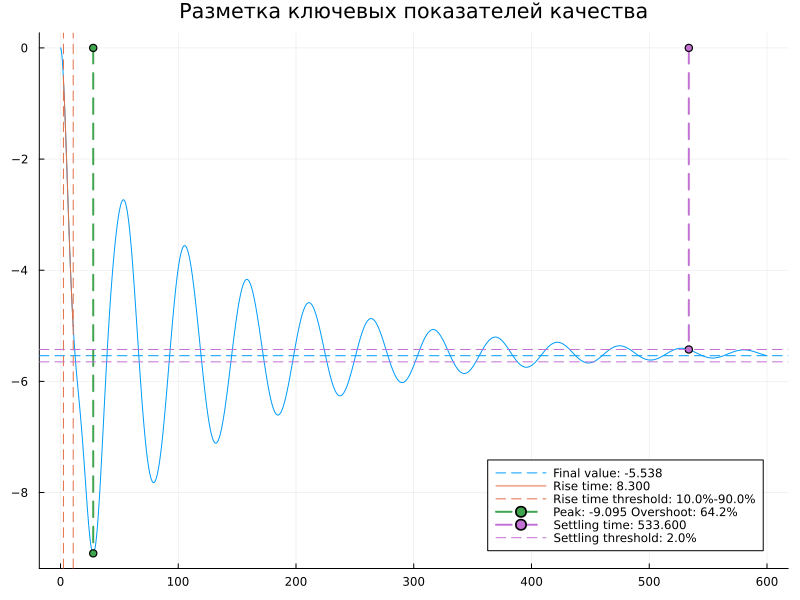
2.3. Определить по графикам переходных процессов значения ключевых показателей качества: величина установившейся ошибки, перерегулирования, время переходного процесса. Определение показателей качества показать на графике. Результаты свести в таблицу.

Ключевые показатели качества: Снимок экрана 2025-06-20 в 12.27.44.png

# @markdown ##### Построение ключевых показателей качества

w2res = step(W2, t)

w2info = stepinfo(w2res)
plot(w2info, lw=[1 1 1 1 2 2], title="Разметка ключевых показателей качества", size=(800, 600))

Рис. 5. Разметка ключевых показателей качества

2.4. Для рассматриваемой подсистемы и заданного входного воздействия, соответствующих индивидуальному варианту задания, аналитически определить величину устранившейся ошибки по положению, по скорости и по ускорению. Результаты свести в таблицу, сделать вывод о порядке астатизма системы.

3. Построение и исследование частотных характеристик системы

3.1. Для рассматриваемой подсистемы и заданного входного воздействия, соответствующих индивидуальному варианту задания, вычислить частотную характеристику для вектора частот из 1000 точек в диапазоне 0.01 ... 100− Гц с использованием функции freqresp(), а затем построить самостоятельно график ЛАФЧХ (диаграмму Боде) с использованием двух subplot и функции semilogx().

Примечание №1. Вектор частот целесообразно задать не линейно распределенным в диапазоне 2 2 10 ...10− Гц, а логарифмически для чего можно использовать функцию logspace(). Функция freqresp() по умолчанию принимает значение частоты в рад/с. Функция freqresp() формирует выход для многомерной системы, поэтому в выходной переменной функции вектор значений частотной характеристики представлен как, так называемая «страница», т.е. имеет размерность не 1000x1 , а 1000x1x1. Для того, чтобы избавиться от лишней размерности (т.к. рассматривается только скалярная передаточная функция) можно воспользоваться функцией squeeze(). Вычисление значений магнитуды и фазы реализовать непосредственно по формулам из лекций.

# @markdown ##### Рассчет и построение лафчх W2
to_degrees = range(-3, 3, length=1000)

f = [10^x for x = to_degrees]
ω = 2 * π * f

amp_dB_2, phase_deg_2 = calc_lfch(W2, ω)
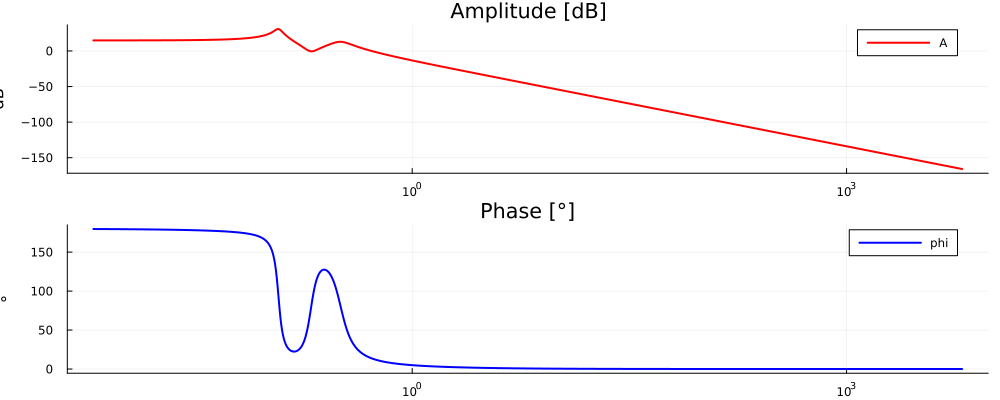
plot_lfch2 = plot_lfch(ω, amp_dB_2, phase_deg_2)

Рис. 6. ЛАФЧХ W_12

3.2. Повторить пункт задания 3.1, но для построения годографа Найквиста

Примечание. При построении годографа Найквиста учесть отрицательные значения частот и дополнительно отметить точку (-1, 0j) с использованием функции scatter(), а также нарисовать окружность, проходящую через точку (-1, 0j) для последующего определения запасов устойчивости.

# @markdown ##### Рассчет и построение годографа Найквиста W2

to_degrees = collect(range(-10, 10, length=1000))
f = [-1 * 10^x for x in reverse(to_degrees)]
append!(f, reverse(-f))
ω = 2 * π * f

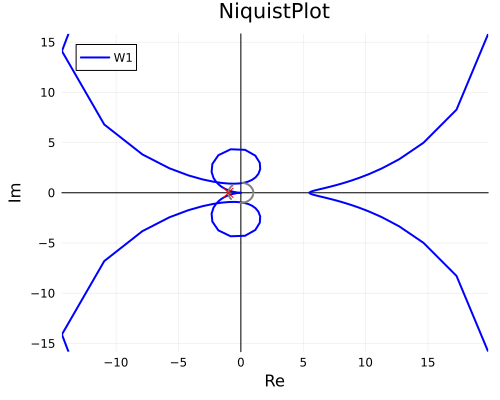
my_niquist_plot = nyquistplot(-W2, ω, unit_circle=true, label="W1", xlabel="Re", ylabel="Im", title="NiquistPlot", color=:blue, lw=2, size=(500, 400))

Рис. 7. Годограф Найквиста W_12

3.3. Определить запасы устойчивости по амплитуде и по фазе (по полученным графикам ЛАФЧХ и годографу Найквиста), показатель колебательности, частоту среза и полосу пропускания системы. Определение показателей качества показать на графиках. Результаты свести в таблицу.

# @ markdown ##### Показатель колебательности(M), частота среза (ω_c) и полоса пропускания (BW)

ω = exp10.(range(log10(1e-3), stop=log10(1e3), length=10000))

resp = freqresp(W2, ω)
mag = dropdims(abs.(resp), dims=(1,2))

A_max, idx_max = findmax(mag)
dc_gain = abs(evalfr(W2, 0)[1])

M = A_max / dc_gain    

level_bw = dc_gain / sqrt(2)
level_c = 1

idx_bw = idx_max
while idx_bw < length(ω) && mag[idx_bw] > level_bw
    idx_bw += 1
end

idx_c = idx_max
while idx_c < length(ω) && mag[idx_c] > level_c
    idx_c += 1
end

if idx_bw >= length(ω)
    BW = Inf
else
    BW = ω[idx_bw]
end

if idx_c >= length(ω)
    ω_c = Inf
else
    ω_c = ω[idx_c]
end

;
# println("M = $(round(M, digits=4))\n")
# println("ω_c = $(round(ω_c, digits=4))\n")
# println("BW = $(round(BW, digits=4))")

# @markdown ##### Построение запасов устойчивости

p1 = marginplot(W2, 
    linecolor = [:red :blue],
    gainpoint_color = :green,  
    phasepoint_color = :purple,
    legend = false,
    title = "marginplot"
)
scatter!(p1[1], [ω[idx_max]], [A_max], color=:green)
annotate!(p1[1], (ω[idx_max] + 0.12, A_max, text("A_max", :green, 8)))

scatter!(p1[1], [ω_c], [level_c], color=:black)
annotate!(p1[1], (ω_c + 0.08, 0.4, text("ω_c", :black, 8)))

scatter!(p1[1], [BW], [level_bw], color=:black)
annotate!(p1[1], (BW + 0.08, 6.5, text("BW", :blue, 9)))

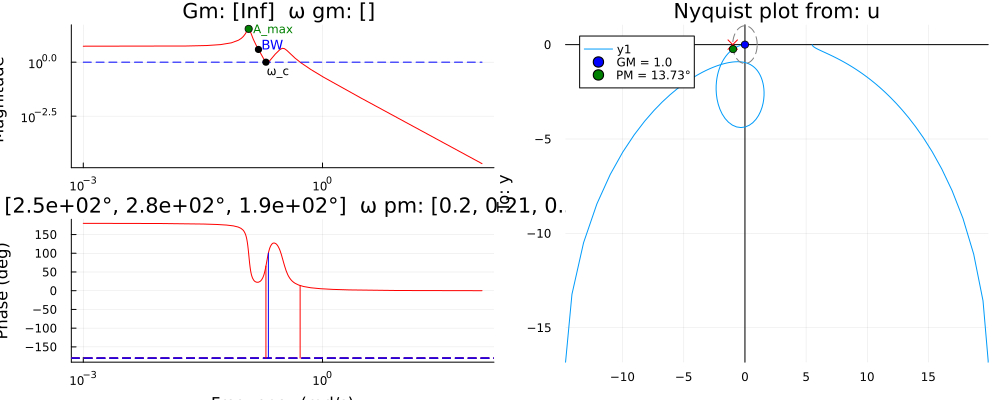
p2 = nyquist_marginplot(-W2)
plot(p1, p2, size=(1000, 400), layout=(1, 2))

Рис. 8. Показатели качества на графиках

4. Исследование устойчивости по полюсам системы.

4.1. Для рассматриваемой подсистемы, соответствующей индивидуальному варианту задания, заданной в пространстве состояний, определить собственные значения матрицы состояния с использованием функции `eigs()`.

# @markdown ##### Поиск собственных значений матрицы состояния
eigs = eigvals(A)

println(join(["Собственные значения:\n", round.(eigs, digits=4)...], "\n  "))

Собственные значения:

  -1.1019 - 0.9948im
  -1.1019 + 0.9948im
  -0.051 - 0.3153im
  -0.051 + 0.3153im
  -0.0071 - 0.1191im
  -0.0071 + 0.1191im

4.2. Для рассматриваемой подсистемы, соответствующей индивидуальному варианту задания, с использованием функций `pole()` и `zero()` определить нули и полюса системы, построить самостоятельно с использованием `scatter()` карту нулей и полюсов.

4.3. По полученной карте нулей и полюсов определить корневые показатели качества. Определение показателей качества показать на графике. Результаты свести в таблицу.

# @markdown ##### Поиск полюсов системы
sys_poles = pole(W2)
println(join(["Полюса:\n",  round.(sys_poles, digits=4)...], "\n  "))

Полюса:

  -0.0071 + 0.1191im
  -0.0071 - 0.1191im
  -0.051 + 0.3153im
  -0.051 - 0.3153im
  -1.1019 + 0.9948im
  -1.1019 - 0.9948im

# @markdown ##### Поиск нулей системы 

sys_zeros = tzeros(W2)
println(join(["Нули:\n", round.(sys_zeros, digits=4)...], "\n  "))

Нули:

  -1.1 + 0.995im
  -1.1 - 0.995im
  -0.02 + 0.199im
  -0.02 - 0.199im

# @markdown ##### изборазим карту нулей и полюсов
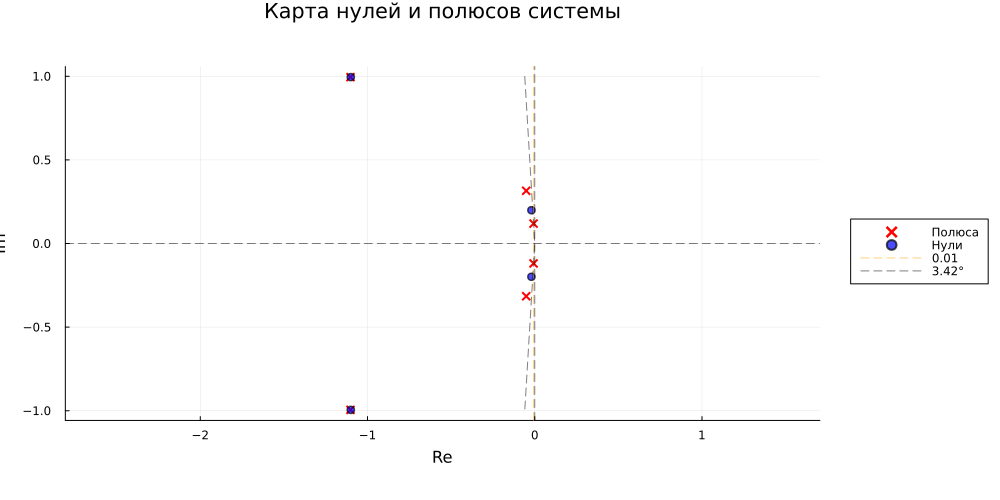
plot(
    title = "Карта нулей и полюсов системы",
    xlabel = "Re",
    ylabel = "Im",
    grid = true,
    legend = :topright,
    aspect_ratio = :equal
)

scatter!(
    real.(sys_poles), 
    imag.(sys_poles),
    label = "Полюса",
    markershape = :x,
    markercolor = :red,
    markersize = 4,
    markerstrokewidth = 2
)
scatter!(
    real.(sys_zeros), imag.(sys_zeros),
    label = "Нули",
    markershape = :circle,
    markercolor = :blue,
    markersize = 4,
    markerstrokewidth = 1.5,
    markeralpha = 0.7,
    legend=:outerright
)

hline!([0], line = (:black, :dash, 0.5), label = "")
vline!([0], line = (:black, :dash, 0.5), label = "")

ha = max(real(sys_poles)...)
hp = min(abs.(angle.(sys_poles))...)

vline!([ha], line= (:orange, :dash, 0.5), label = "$(round(-ha, digits=2))")

dp = (hp - pi/2)*180/pi
plot!(
    [cos(hp), 0, cos(-hp)], 
    [sin(hp), 0, sin(-hp)], 
    line=(:black, :dash, 0.5), 
    label="$(round(dp, digits=2))°", 
    size=(1000, 500)
)

Рис. 9. карта нулей и полюсов

5. Исследование устойчивости по косвенным критериям.

5.1. Для рассматриваемой подсистемы, соответствующей индивидуальному варианту задания, аналитически определить устойчивость системы с использованием критериев: а) Гурвица; б) Рауса.

Характеристический палином:

Матрица Гурвица

Приведем матрицу Гурвица к верхнетреугольному виду

Посчитаем определители. Система устойчива

Все множители определителей положительны, значит и все определители - положительны. Тогда система устойчива по критерию Гурвица.

Таблица Рауса

все элементы в первом столбце положительны, значит система устойчива по критерию Рауса

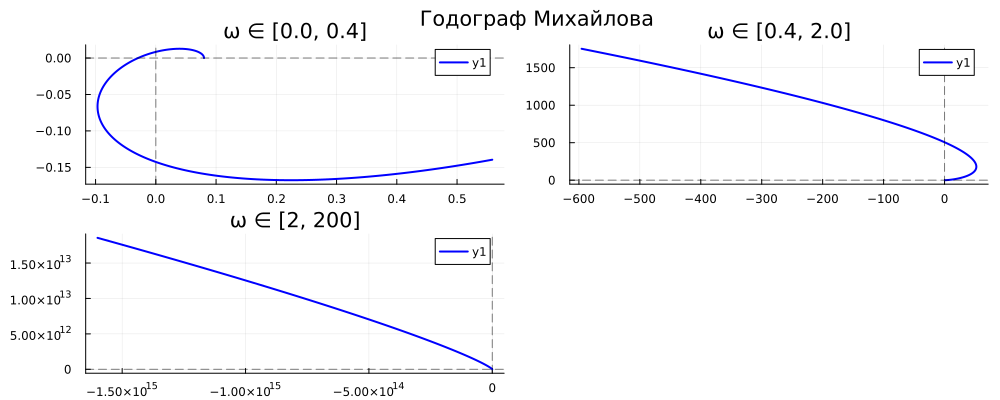
5.2. Для рассматриваемой подсистемы, соответствующей индивидуальному варианту задания, определить устойчивость разомкнутой системы по критерию Михайлова (требуется построить соответствующий график).

Примечание. Построение годографа Михайлова осуществляются по характеристическому полиному знаменателя передаточной функции. Для этого необходимо сначала с использованием функции tfdata() из нужной передаточной функции выделить два вектора коэффициентов – полиномов числителя и знаменателя. Затем необходимо создать новую передаточную функцию с использованием tf(), для которой в качестве коэффициентов полинома числителя задать коэффициенты полинома знаменателя заданной передаточной функции, полученные ранее, а в качестве коэффициентов полинома знаменателя указать 1. В результате получится передаточная функция, которая соответствует полиному знаменателя заданной передаточной функции. Затем для построения годографа Михайлова воспользоваться аналогичной процедурой, примененной в п. 3.2.

Для всех трех передаточных функций знаменатель одинаков, так что годограф михайлова будет один.

# @markdown ##### Годограф Михайлова
s = tf("s")
Ds = 25*s^6 + 58*s^5 + 64.44*s^4 + 12.96*s^3 + 6.68*s^2 + 0.24*s + 0.08

p1 = mich_plot(Ds, [0:0.001:0.4;])
p2 = mich_plot(Ds, [0.4:0.001:2;])
p3 = mich_plot(Ds, [2:200;])

plot(p1, p2, p3, plot_title="Годограф Михайлова\n\n", plot_titlefontsize=14, size=(1000, 400))

Рис. 10. Годограф Михайлова

По критерию михайлова система устойчива, так как годограф начинается на положительной части действительной оси, и проходит 6 квадрантов по порядку против часовой стрелки, и уходит в бесконечность, проходя 6 квадрант, а система без обратной связи имеет 6 порядок.

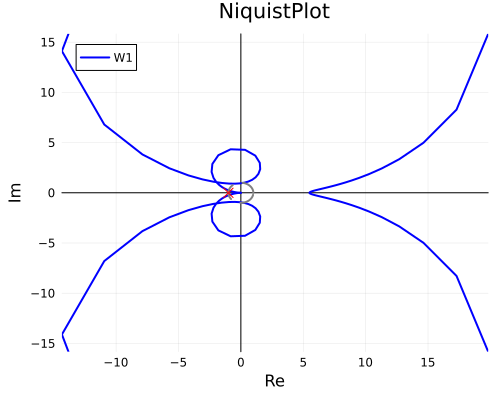
5.3. Для рассматриваемой подсистемы, соответствующей индивидуальному варианту задания, определить устойчивость замкнутой системы по критерию Найквиста.

my_niquist_plot

Рис. 11. Годограф Найквиста

Годограф Разомкнутой системы огибает точку (-1, 0j) 0 раз, значит система устойчива.

6. Реализация последовательной и параллельной коррекции.

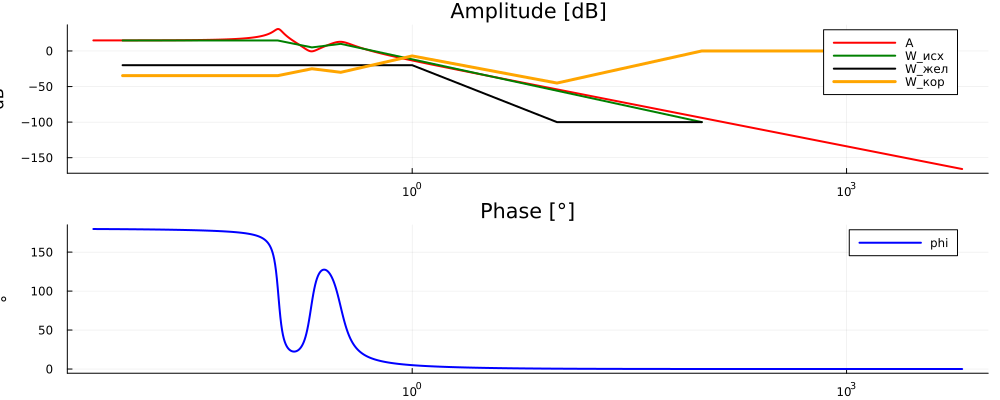
6.1. Для рассматриваемой подсистемы, соответствующей индивидуальному варианту задания, провести расчет последовательного корректирующего устройства таким образом, чтобы на диапазоне частот 10^{-1} ... 10^{0}− Гц коэффициент усиления системы был равен -20 дБ (плато), а на диапазоне частот выше 10 Гц не превышал значения -100 дБ. Построить соответствующие графики ЛАЧХ на которых отобразить: ЛАЧХ исходной системы, желаемую ЛАЧХ, ЛАЧХ корректирующего устройства, ЛАЧХ скорректированной системы. Построение графиков повторить для случая асимптотического построения ЛАЧХ

Построение асимптот для коррекции

# @markdown ##### Построение асимптот для коррекции
plot!(plot_lfch2[1],[1e-2, 0.118, 0.203, 0.321, 100], [14.7, 14.7, 5, 10, -100], label="W_исх", color=:green, lw=2)
plot!(plot_lfch2[1], [1e-2, 1, 10, 100], [-20, -20 , -100, -100], label="W_жел", color=:black, lw=2)
plot!(plot_lfch2[1], [0.01, 0.118, 0.203, 0.321, 1, 10, 100, 1000], [-34.7, -34.7, -25, -30, -7, -45.1, 0, 0], label="W_кор", color=:orange, lw=3)
plot_lfch2

Рис. 12. ЛАФЧХ, и асимптоты коррекции

Расчет звеньев корректирующего устройства

На интервале (0, 0.118) график корректирующей функции - горизонтальная линия (угол наклона - 0) на уровне -34.7 dB, значит корректор будет иметь коэффициент K

На интервале (0.118, 0.203) функция имеет угол наклона ≈ + 40 db/dec, нужно увеличить угол наклона на +40. Также в точке 0.118 исходная функция имеет пик, направленный вверх. Его будет разумно скомпенсировать при помощи добавления звена, обратного колебательному. Значение ε ≈ 0.062 - подобрано "экспериментально". Таким образом передаточная функция ПКУ имеет следующий множитель.

На интервале (0.203, 0.321) функция имеет угол наклона ≈ - 40 db/dec, нужно изменить угол наклона на -80. Также в точке 0.203 исходная функция имеет пик, направленный вниз. Его будет разумно скомпенсировать при помощи добавления колебательного звена ε ≈ 0.1 - подобрано "экспериментально".

Колебательное звено имеет меняет асимптотический угол наклона на -40. еще -40 получим при помощи апериодического звена второго порядка, T1 и T2 которого примерно равны.

Таким образом передаточная функция ПКУ имеет следующие множители.

На интервале (0.321, 1) функция имеет угол наклона ≈ + 80 db/dec, нужно изменить угол наклона на +120. Также в точке 0.321 исходная функция имеет пик, направленный вверх. Его будет разумно скомпенсировать при помощи добавления звена, обратного колебательному. Значение ε ≈ 0.15 - подобрано "экспериментально".

Колебательное звено имеет меняет асимптотический угол наклона на -40, значит звено, обратное ему - на +40 еще +40 получим при помощи форсирующего звена четвертого порядка, T1, T2, T3 и T4 которого примерно равны.

Таким образом передаточная функция ПКУ имеет следующие множители.

На интервале (1, 10) функция имеет угол наклона ≈ - 60 db/dec, нужно изменить угол наклона на -140.

Этого можно добиться при помощи апериодического звена седьмого порядка, T1, T2, T3, T4, T5, T6 и T7 которого примерно равны.

Таким образом передаточная функция ПКУ имеет следующий множитель.

На интервале (10, 100) функция имеет угол наклона ≈ + 40 db/dec, нужно изменить угол наклона на +100.

Этого можно добиться при помощи форсирующего звена пятого порядка, T1, T2, T3, T4 и T5 которого примерно равны.

Таким образом передаточная функция ПКУ имеет следующий множитель.

На интервале (100, + ∞) функция имеет угол наклона ≈ 0 db/dec и лежит на нулевом уровне, нужно изменить угол наклона на +-40.

Этого можно добиться при помощи апериодического звена второго порядка, T1 и T2 которого примерно равны.

Таким образом передаточная функция ПКУ имеет следующий множитель.

# @markdown ##### Рассчет корректирующего устройства

@syms s

ε = 0.15
K = 10^(-34.7/20)
M1 = (s^2 + 2 * 0.118 * 0.062 * s + 0.118^2) / 0.118^2
M21 = 0.203^2 / (s^2 + 2 * 0.203 * 0.1 * s + 0.203^2)
M22 = 1 / (1/0.203 * s + 1)^2
M31 = (s^2 + 2 * 0.321 * ε * s + 0.321^2) / 0.321^2
M32 = (1/0.321 * s + 1)^4
M4 = 1/ (s + 1)^7
M5 = (1/10*s + 1)^5
M6 = 1/(1/100*s + 1)
W2_kor_sym = simplify(K * M1 * M21 * M22 * M31 * M32 * M4 * M5 * M6);

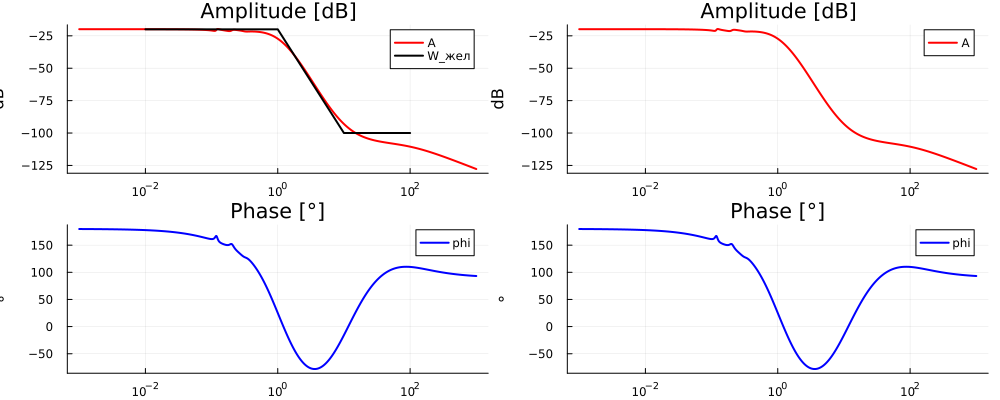
Построение ЛАФЧХ скорректированного устройства

# @markdown ##### Построение ЛАФЧХ

W2_kor = sym_to_tf(W2_kor_sym, s)
W2_res = W2 * W2_kor
amp_dB_kor, phase_deg_kor = calc_lfch(W2_res, ω)
p1 = plot_lfch(ω, amp_dB_kor, phase_deg_kor)
p2 = plot_lfch(ω, amp_dB_kor, phase_deg_kor)
plot!(p1[1], [1e-2, 1, 10, 100], [-20, -20 , -100, -100], label="W_жел", color=:black, lw=2)
plot(p1, p2)

Рис. 13. ЛАФЧХ Скорректированного устройства

Анализ непрерывных динамических систем