Анализатор спектра spectrumAnalyzer
Анализатор спектра spectrumAnalyzer
В составе библиотеки EngeeDSP есть продвинутый инструмент для оценки и визуализации спектров сигналов - системный объект spectrumAnalyzer. Рассмотрим базовые сценарии его применения для задач спектрального анализа различных сигналов, а также узнаем, как изменять параметры объекта.
Методы оценки спектра
В данном разделе мы познакомимся с основными параметрами объекта EngeeDSP.spectrumAnalyzer, и, в частности, с доступными на выбор методами оценки спектра - банком фильтров и методом Уэлча.
Первый тестовый сигнал:
Для начала создадим тестовый сигнал x для анализа. Это сумма двух синусоид и гауссовского шума. Частота дискретизации сигнала Fs равна 20 МГц, основные частоты синусоид - 2 МГц и 4 МГц (синусоида с большей частотой имеет амплитуду 0.25). Также важно отметить, что для анализа мы выбрали сигнал длительностью nsamp = 40 000 отсчётов.
Fs = 20e6;
dt = 1/Fs;
nsamp = 40000;
t = 0:dt:(nsamp*dt)-dt;
f1 = 2e6;
f2 = 4e6;
x = sin.(2*pi*f1*t) .+ 0.25*sin.(2*pi*f2*t) + randn(length(t));
plot(t,x, xlim = (0,t[200]), leg = false)
Убедимся, что сигнал на всей протяженности колеблется вокруг нуля. Используем функцию std библиотеки EngeeDSP:
EngeeDSP.Functions.std(x)
Мы наблюдаем математическое ожидание, близкое к нулю.
Системный объект spectrumAnalyzer
Создадим системный объект scope1 типа EngeeDSP.spectrumAnalyzer. Укажем явно некоторые из параметров, а именно частоту дискретизации SampleRate и представление спектра (одностороннее). Остальные значения параметров оставим по-умолчанию.
scope1 = EngeeDSP.spectrumAnalyzer();
scope1.SampleRate = Fs;
scope1.PlotAsTwoSidedSpectrum = false;
scope1
Отображается обширный список доступных для модификации параметров, но пока что отметим параметр метода оценки спектра Method = "filter-bank", тип отображения "спектр мощности" SpectrumType = "power", ViewType = "spectrum", а также установку разрешения по частоте RBWSource в значение "auto".
Если подать на "вход" переменной scope1 наш тестовый сигнал x, то автоматически выведется график спектра мощности сигнала. Кстати, название графика и подписи по осям также являются параметрами системного объекта. Установим значение поля Title, и вызовем объект:
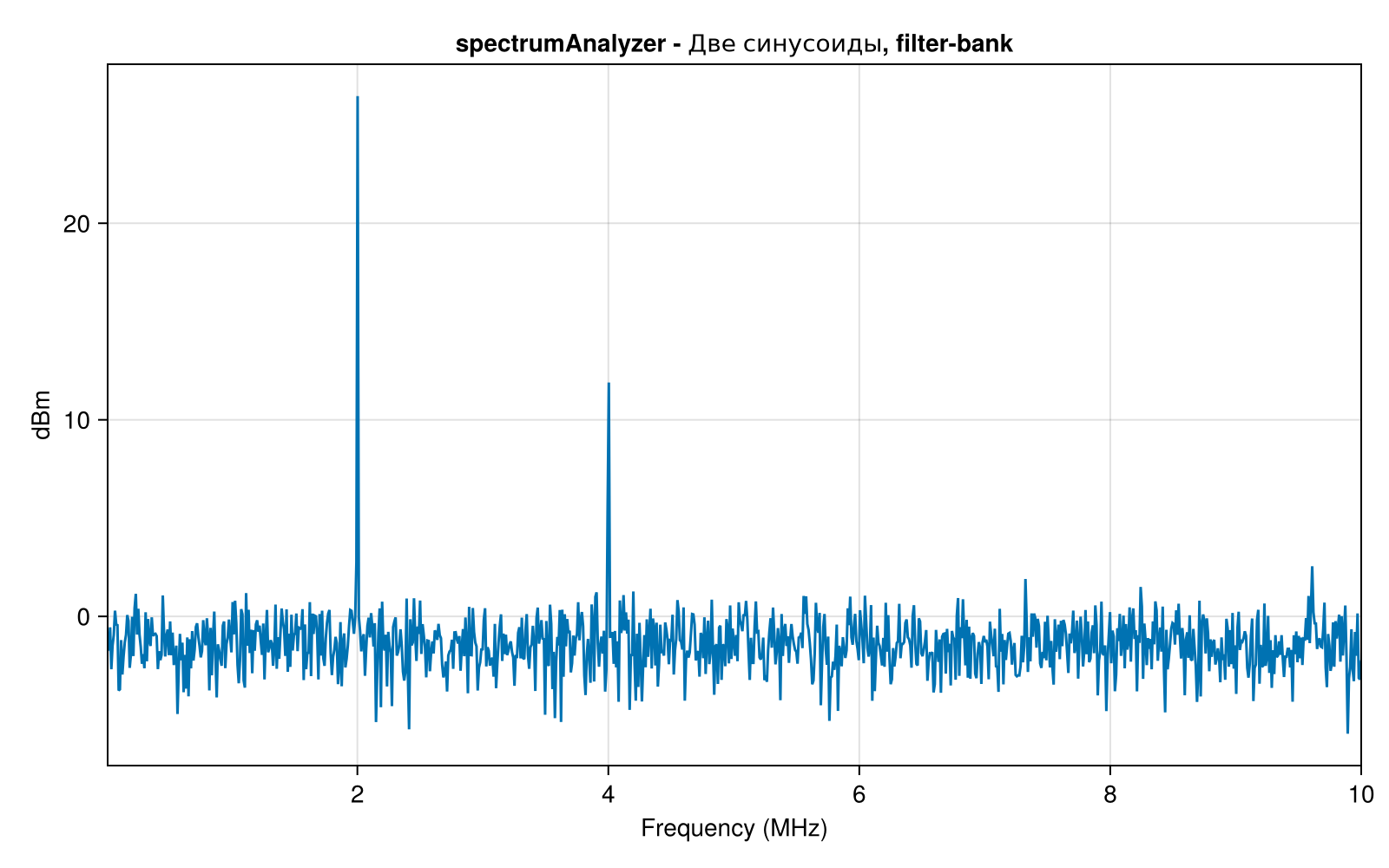
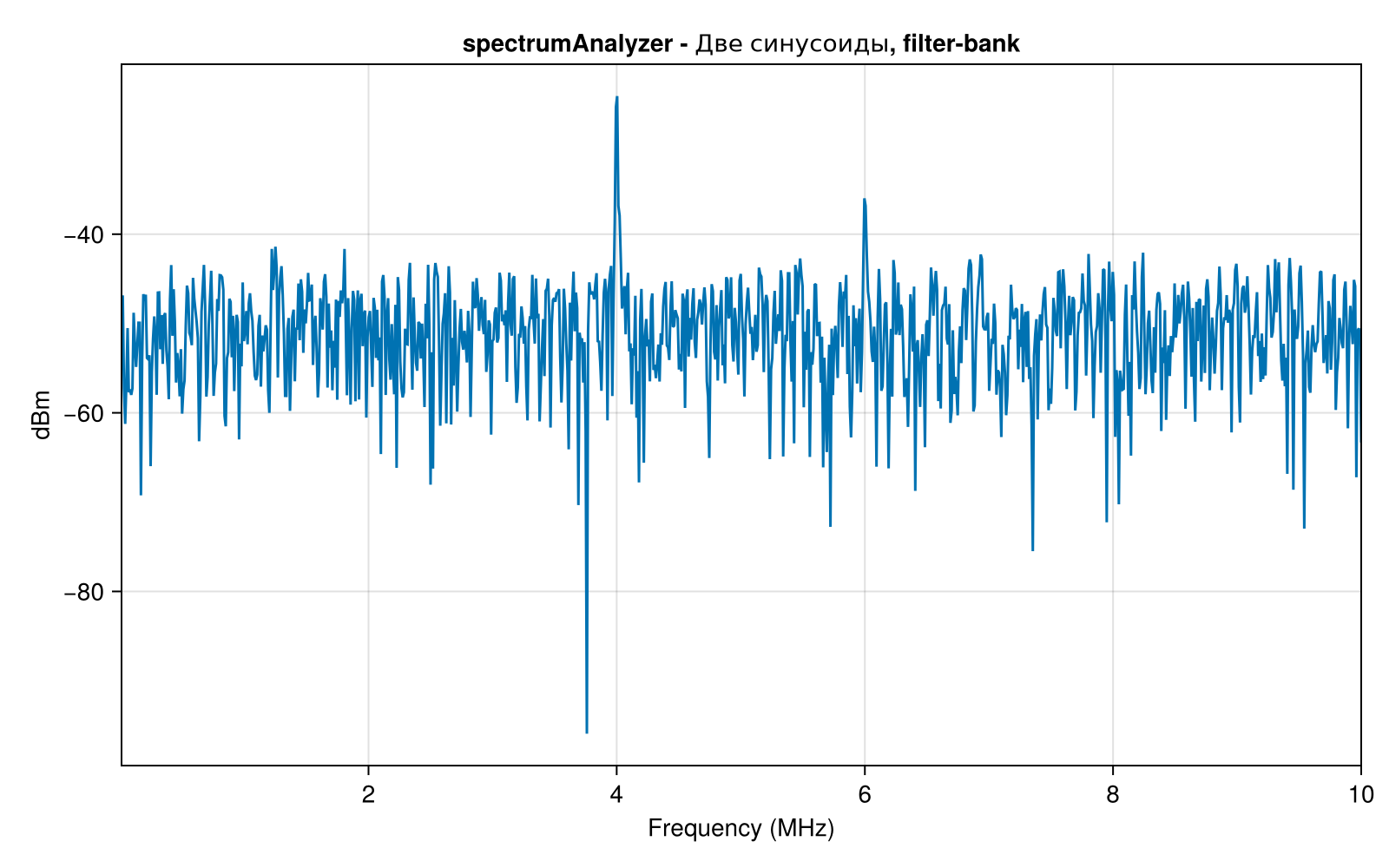
scope1.Title = "spectrumAnalyzer - Две синусоиды, filter-bank";
scope1(x)
Банк фильтров - это набор из множества фильтров (обычно полосовых), которые перекрывают весь исследуемый частотный диапазон. Многие реальные устройства - анализаторы спектра - используют банки фильтров для разбиения сигнала на множество частотных полос. Это позволяет анализировать спектр сигнала более детально, поскольку он разбивается на подканалы (в банке анализа), а затем может быть восстановлен (в банке синтеза).
Подробнее о методе можно почитать здесь.
Запись отсчётов спектра в переменную
Функция getSpectrumData позволяет получить численные отсчёты значений спектра в виде вектора или матрицы. В словарь spectrumdata мы поместим значения частот и отсчётов спектра мощности. Затем отобразим спектр при помощи переменных f1 и s1 на стандартном графике функцией plot. Теперь мы можем интерактивно и программно оценить уровень мощности и положение пиков, соответствующих тестовым синусоидам:
spectrumdata = EngeeDSP.getSpectrumData(scope1);
f1 = spectrumdata["frequencies"];
s1 = spectrumdata["spectrum"];
plot(f1,s1,leg=false)
Метод Уэлча
Метод Уэлча - это один из базовых способов оценки спектра сигнала на основе быстрого преобразования Фурье (БПФ). Находит широкое применение для большинства задач спектрального анализа, особенно когда обработка происходит не в реальном времени и важна простота настройки.
Создадим ещё один системный объект анализатора спектра scope2, но в этот раз укажем метод Уэлча, как основной для оценки. Также поменяем параметры таким образом, чтобы мы могли явно контролировать разрешение по частоте RBW, и установим его значение в 20 000 Гц.
scope2 = EngeeDSP.spectrumAnalyzer();
scope2.SampleRate = Fs;
scope2.PlotAsTwoSidedSpectrum = false;
scope2.Method = "welch";
scope2.RBWSource = "property";
scope2.RBW = 2e4;
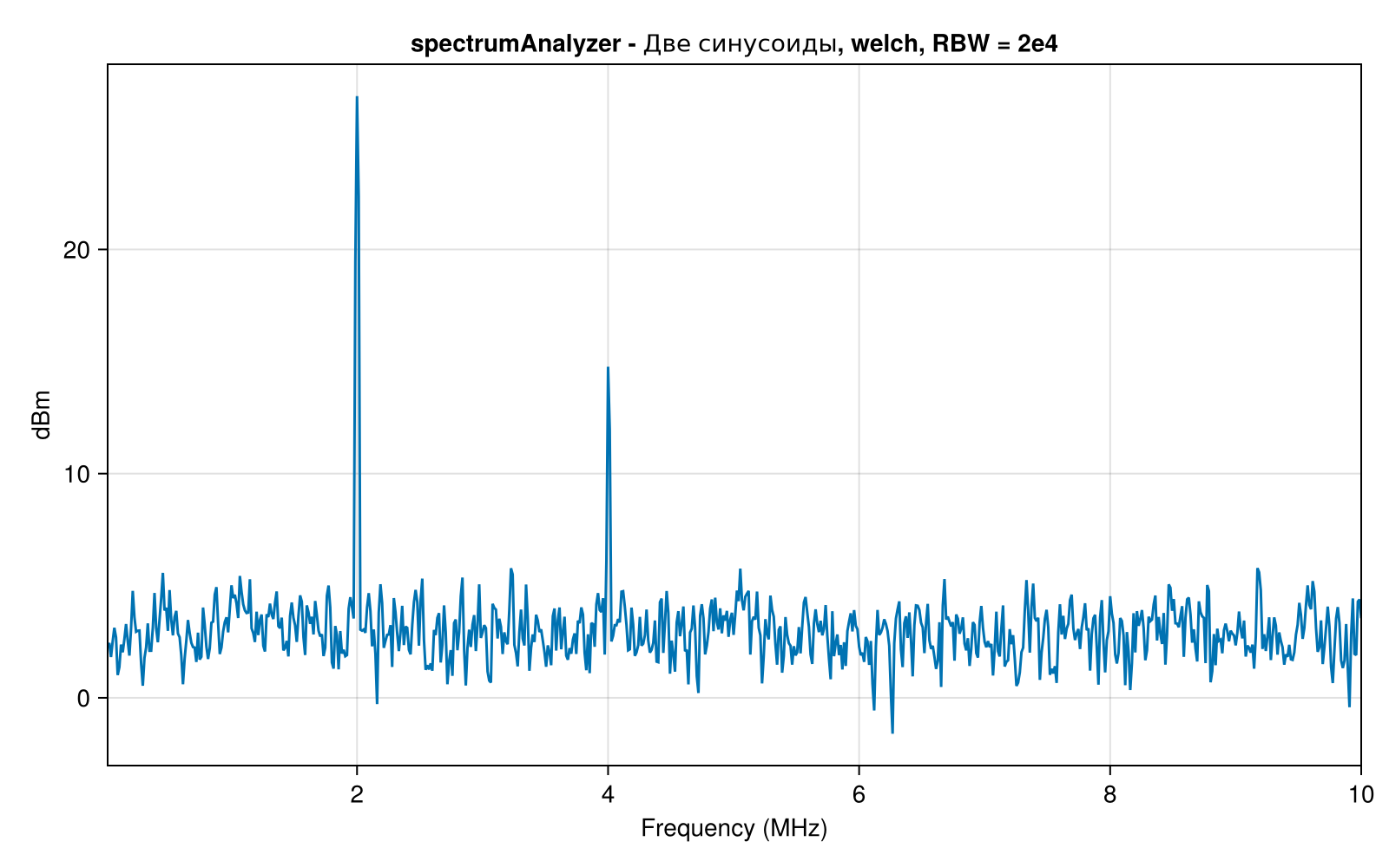
scope2.Title = "spectrumAnalyzer - Две синусоиды, welch, RBW = 2e4";
scope2(x)
Сравним значения отсчётов оценки спектра мощности двумя методами, отобразим результаты на одном графике:
welchdata = EngeeDSP.getSpectrumData(scope2);
f2 = welchdata["frequencies"];
s2 = welchdata["spectrum"];
plot(f1,s1, label = "filter-bank")
plot!(f2,s2, label = "welch", title = "Сравнение методов")
Меняя разрешение по частоте при использовании метода Уэлча можно также наблюдать изменение уровня шума. А при использовании метода банка фильтров важно следить за длительностью сигнала, и при поступлении коротких "отрезков" - накапливать их для точной оценки энергетики.
Спектры нестационарных сигналов
Воспользуемся функционалом объекта spectrumAnalyzer для оценки спектра сигнала, изменяющегося по своему частотному составу во времени. Типичный сигнал для подобного анализа - с частотной модуляцией.
Создадим сигнал, частота которого линейно возрастает с течением времени, то есть сигнал с линейной частотной модуляцией (ЛЧМ). Для этого воспользуемся функцией chirp из библиотеки EngeeDSP:
LFM = EngeeDSP.Functions.chirp(t,0,t[end],7e6);
plot(t,LFM, xlim = (0,t[2000]), label = "ЛЧМ-сигнал")
Частота сигнала LFM линейно возрастает с 0 до 7 МГц за время "симуляции".
Теперь создадим ещё один объект анализатора спектра и назовём его chirpscope. Зададим его параметры сразу же при инициализации в круглых скобках. Отметим такие параметры, как метод осреднения и коэффициент "забывания", параметры БПФ (кол-во точек, размер окна), процент перекрытия для метода Уэлча и тип оконной функции. От них зависит результирующая форма графика.
chirpscope = EngeeDSP.spectrumAnalyzer(
SampleRate = Fs,
Method = "welch",
SpectrumType = "power",
AveragingMethod = "exponential",
ForgettingFactor = 0.99,
Window = "hamming",
WindowLength = 1024,
OverlapPercent = 75,
FrequencyResolutionMethod = "window-length",
FFTLengthSource = "property",
FFTLength = 1024,
PlotAsTwoSidedSpectrum = false,
FrequencySpan = "full",
ReferenceLoad = 1)
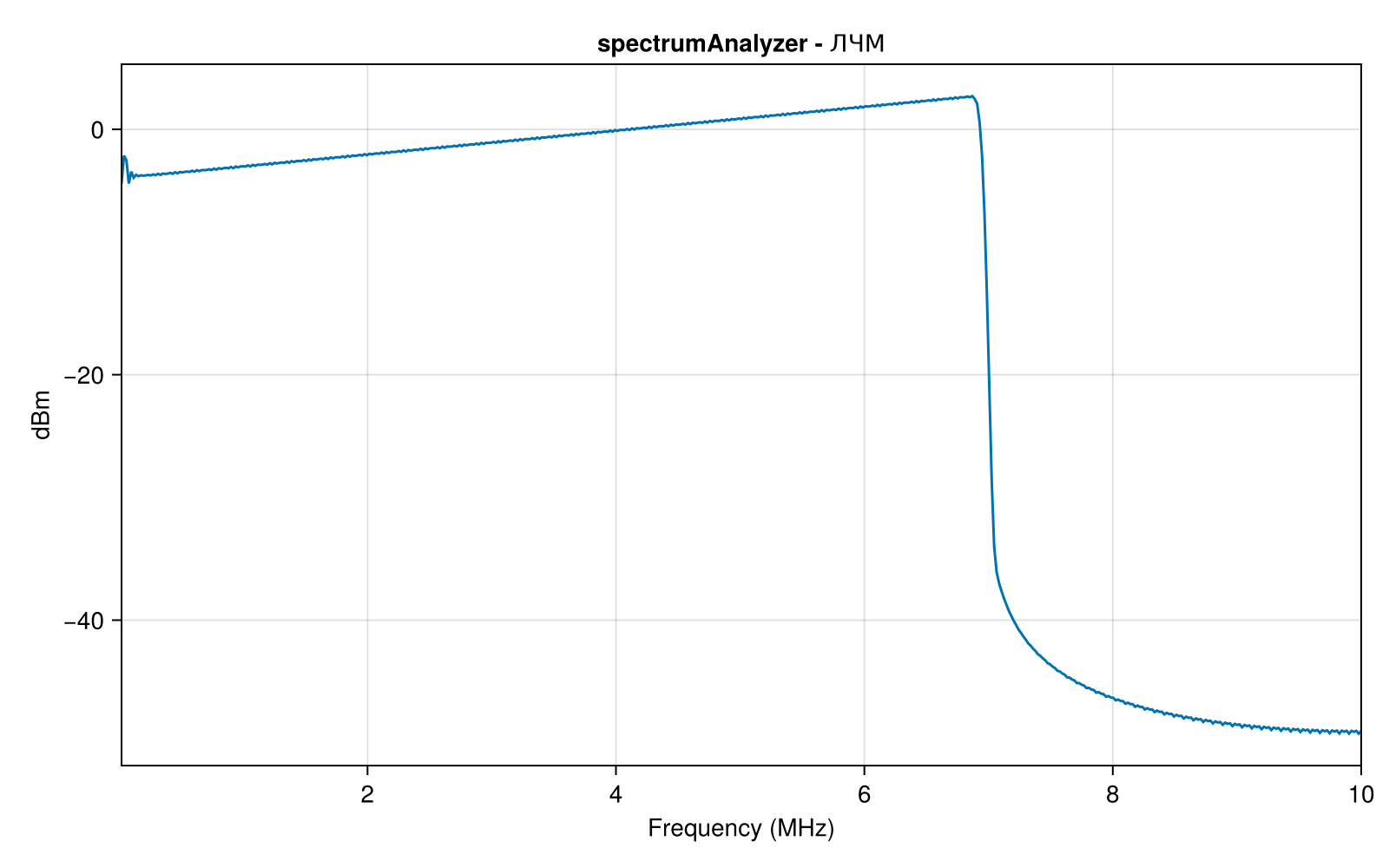
chirpscope.Title = "spectrumAnalyzer - ЛЧМ"
chirpscope(LFM)
При указанных параметрах мы наблюдаем ожидаемую форму спектра ЛЧМ-сигнала, он занимает полосу от 0 до 7 МГц. Впрочем, на подобном графике невозможно наблюдать динамику изменения спектра во времени.
Спектрограмма
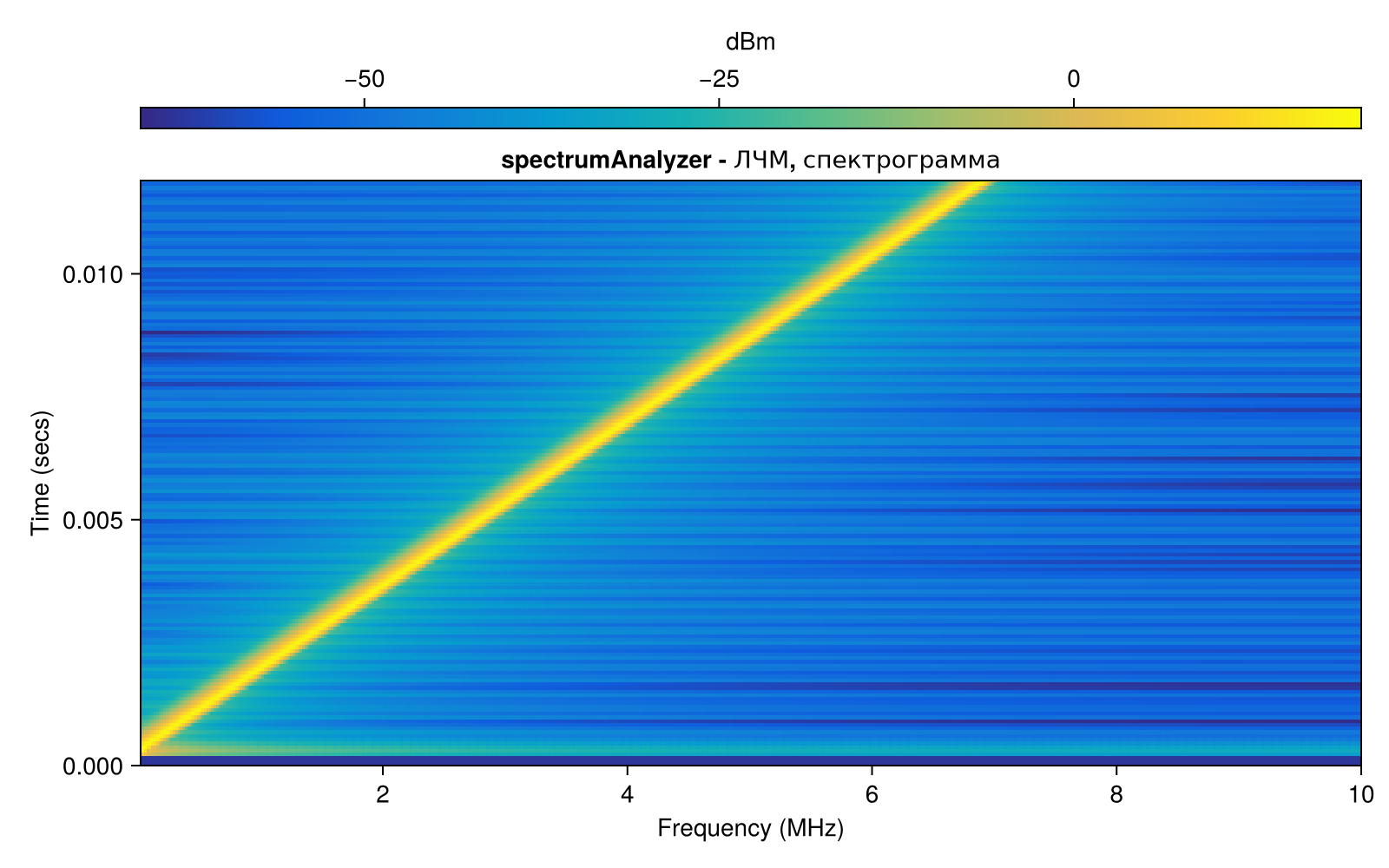
Для отображения спектров нестационарных сигналов в частотной области полезно использовать спектрограмму. Для этого нам необходимо изменить некоторые из параметров нашего объекта chirpscope:
release!(chirpscope)
chirpscope.ViewType = "spectrogram";
chirpscope.ForgettingFactor = 0.2;
chirpscope.RBWSource = "property";
chirpscope.RBW = 1e5;
chirpscope.TimeSpanSource = "property";
chirpscope.TimeSpan = 0.012;
chirpscope.Colormap = "parula";
chirpscope.Title = "spectrumAnalyzer - ЛЧМ, спектрограмма";
chirpscope(LFM)
Накопление и осреднение спектра
При работе с потоковыми сигналами для более точной оценки энергетики полезных исследуемых спектральных компонентов и снижения шума используются техники накопления и осреднения спектров, рассчитанных на последовательно поступающих временных отрезках сигнала. Рассмотрим этот процесс в динамике.
Системный объект SineWaveDSP
Создадим новый тестовый сигнал, теперь с применением ещё одного системного объекта библиотеки EngeeDSP - источника синусоиды SineWaveDSP. Этот объект позволяет последовательно генерировать отрезки неразрывного синусоидального сигнала. В нашем случае, мы будем разбивать длинный входной сигнал на отрезки по 5000 отсчётов (параметр fSz):
fSz = 5000;
sig1 = EngeeDSP.SineWaveDSP();
sig1.Amplitude = 1;
sig1.Frequency = 4e6;
sig1.SampleTime = 1/Fs;
sig1.SamplesPerFrame = fSz;
sig2 = EngeeDSP.SineWaveDSP();
sig2.Amplitude = 0.25;
sig2.Frequency = 6e6;
sig2.SampleTime = 1/Fs;
sig2.SamplesPerFrame = fSz;
plot(sig1() + sig2() + randn(fSz), xlim = (0,100), label = "SineWaveDSP")
Когда мы анализируем условно "короткий" отрезок зашумлённого сигнала при использовании метода банка фильтров мы не можем точно оценить энергетику пиков, а также наблюдаем высокий уровень шума на спектре:
release!(scope1)
scope1(sig1() + sig2() + randn(fSz))
В реальных устройствах сигнал поступает на вход анализатора последовательно, именно такими буферизованными отрезками, и для корректной оценки его необходимо накапливать.
Системный объект spectrumAnalyzer поддерживает различные способы осреднения спектра. Рассмотрим в динамике накопление с осреднением - для этого создадим анимацию последовательного вызова системных объектов источников синусоид с аддитивным гауссовским шумом, и оценки спектра объектом scope1:
release!(scope1)
anim = @animate for i = 1:30
scope1(sig1() + sig2() + randn(fSz));
tempdata = EngeeDSP.getSpectrumData(scope1);
tempf = tempdata["frequencies"];
temps = tempdata["spectrum"];
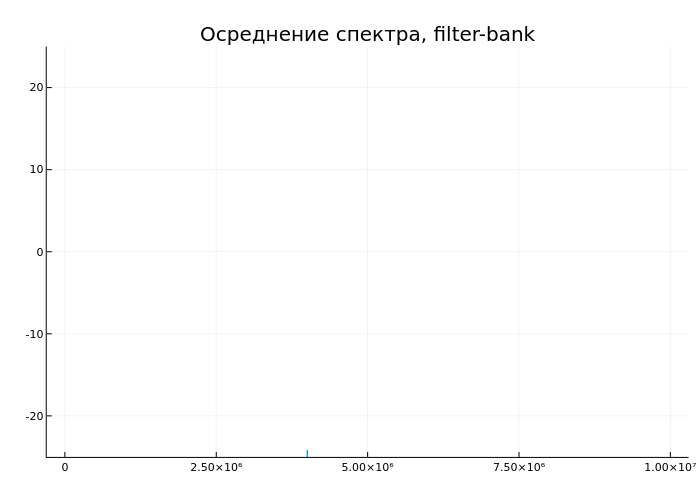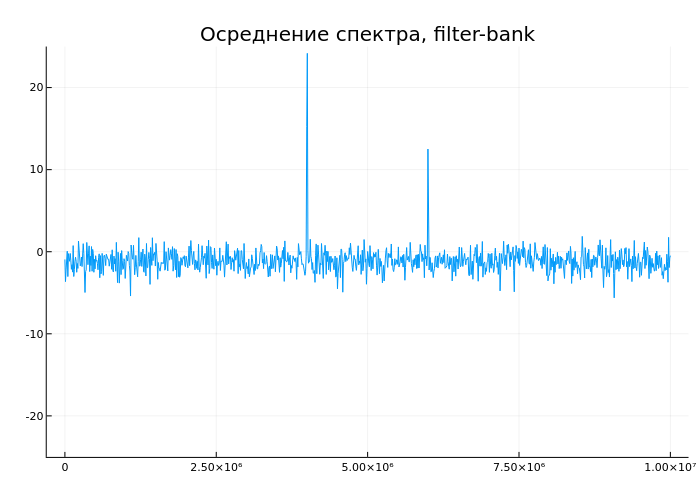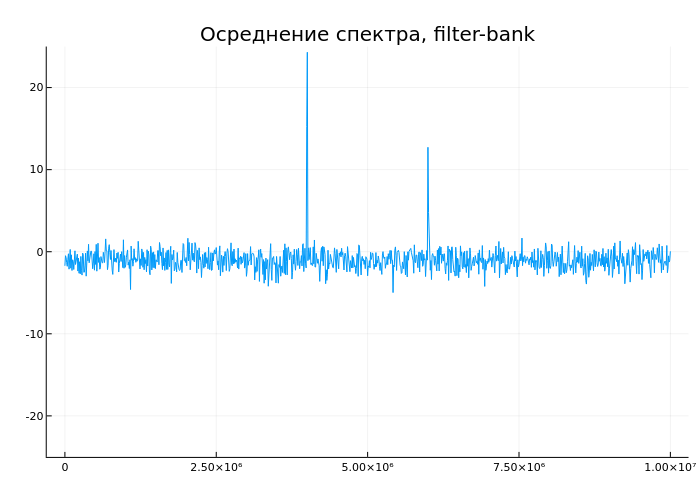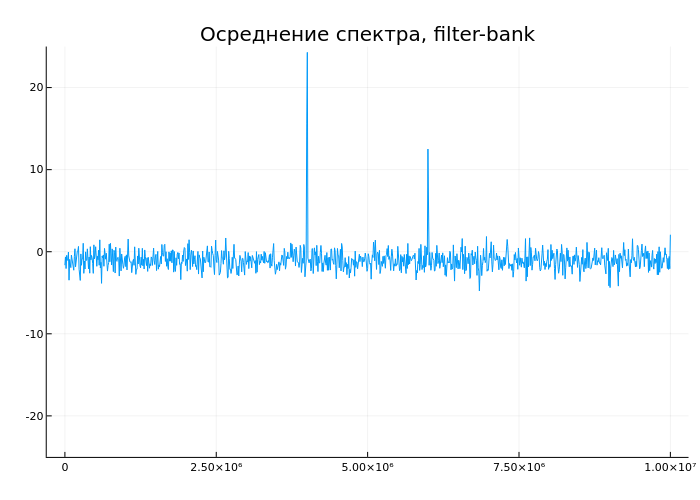
plot(tempf,temps, ylim = (-25,25), leg = false, title = "Осреднение спектра, filter-bank")
end
gif(anim, "spectrum_averaging.gif", fps = 5)
Мы видим постепенное снижение уровня шума а также приближение к точной оценке уровня пиков.
Заключение
Мы познакомились с базовым функционалом системного объекта spectrumAnalyzer библиотеки EngeeDSP. Рассмотрели синтаксис его инициализации и вызова, особенности настройки его параметров, и наблюдали их влияние на результат оценки спектров различных тестовых сигналов.