В 20 раз быстрее чем MATLAB
Сравнение производительности Julia и MATLAB на матричных операциях
Представляем результаты вычислительного эксперимента: оценки того, во сколько раз выполнение матричных операций на Julia позволяет ускорить код относительно таких же операций в MATLAB.
Начнем с подготовки окружения. Установим библиотеки, которые могут не входить в стандартную поставку Engee на момент публикации, затем подключим нужные библиотеки и переведем ядро вывода графиков в не-интерактивный режим.
]add BenchmarkTools StatsPlots
using BenchmarkTools, LinearAlgebra, MATLAB, StatsPlots
gr()
Для информации сравним версии библиотек, используемых обеими системами, для выполнения матричных операций. Существует много реализация библиотек для матричных операций. Как правило, совокупно набор этих функций называется BLAS (Basic Linear Algebra Subroutines, базовые подпрограммы линейной алгебры) и использование той или иной реализации, оптимизированной под те или иные процессоры может быть одним из факторов сравнения.
mat"version -blas"
mat"maxNumCompThreads()"
У MATLAB и Julia различаются не только реализации BLAS, но и количество потоков:
BLAS.get_config()
BLAS.vendor()
BLAS.get_num_threads()
BLAS.set_num_threads(48)
BLAS.get_num_threads()
Мы видим, что MATLAB использует библиотеку oneAPI от Intel, а Julia использует opensource библиотеку libopenblas64. На стороне Engee обеим системам выделены одинаковые ресурсы для тестирования. Можем приступить к сравнению.
Задача перемножения матриц
Решим задачу на Julia, сохранив все результаты выполнения в вектор (выведем только медианные результаты):
sizes = Int.([0.5e2, 1e2, 0.5e3, 1e3, 0.5e4, 1e4])
julia_times = []
for n in sizes
result = @benchmark rand($n,$n) * rand($n,$n);
append!(julia_times, [result.times ./ 1e9]) # ns to sec
end
# Выведем медианное время по каждому запуску для проверки
median.(julia_times)
Мы могли бы сохранять медианное время командой Float64(median(result.times) / 1e9)), но интересно было бы посмотреть графики с допусками, поэтому мы сохраняем все результаты. А теперь решим задачу на ядре MATLAB, которое нам доступно:
@mput sizes # Передать параметры матриц в MATLAB
mat"""
run_times = [];
for i = 1:length(sizes)
n = sizes(i);
testFunc = @() rand(n, n) * rand(n, n); % Определяем функцию для тестирования
t = timeit(testFunc); % Измеряем время выполнения
run_times = [run_times, t]; % Сохраняем в выходной вектор
end
""";
matlab_time = @mget run_times # Получить вектор результатов из MATLAB
Как окружение
@benchmarkв Julia, так и функцияtimeitв MATLAB, обе запускают передаваемую в операцию многократно.
Построим график, который покажет, какого ускорения позволяет добиться Julia:
n_points = length(sizes)
julia_means = zeros(n_points)
julia_stds = zeros(n_points)
for i in 1:n_points
julia_means[i] = mean(julia_times[i])
julia_stds[i] = std(julia_times[i])
end
data_matrix = [julia_means matlab_time']
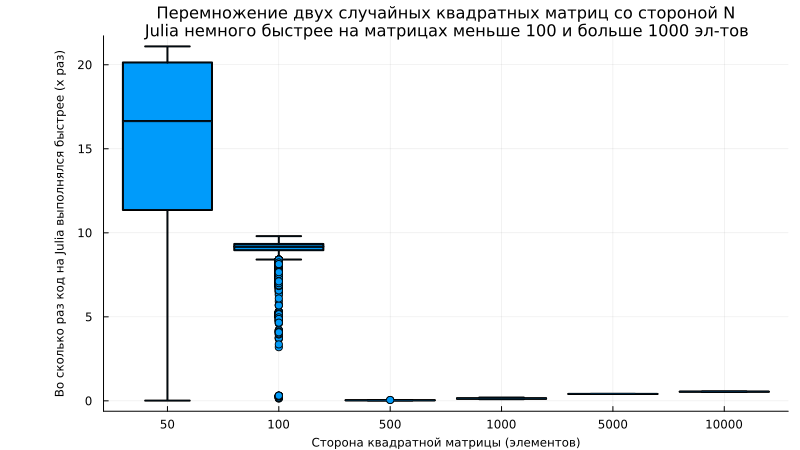
boxplot([matlab_time[i]./julia_times[i] for i in 1:length(sizes)], c=1, legend=false,
xlabel="Сторона квадратной матрицы (элементов)", ylabel="Во сколько раз код на Julia выполнялся быстрее (x раз)",
xticks=(1:length(sizes),sizes), lw=2, guidefont=font(8), left_margin=15Plots.mm, size=(800,450),
title="Перемножение двух случайных квадратных матриц со стороной N\nJulia немного быстрее на матрицах меньше 100 и больше 1000 эл-тов", titlefont=font(11))
Задача возведения в степень
Измерим время выполнения в Julia и в MATLAB:
sizes = Int.([0.5e2, 1e2, 0.5e3, 1e3, 0.5e4, 1e4])
# Измерение в Julia
julia_times = []
for n in sizes
A = rand(n,n);
result = @benchmark $A .^3;
append!(julia_times, [result.times ./ 1e9]) # ns to sec
end
@mput sizes # Передать параметры матриц в MATLAB
mat"""
run_times = [];
for i = 1:length(sizes)
n = sizes(i);
A = rand(n, n); % Создаем случайную матрицу
testFunc = @() A .^ 3; % Определяем функцию для тестирования
t = timeit(testFunc); % Измеряем время выполнения
run_times = [run_times, t]; % Сохраняем в выходной вектор
end
""";
matlab_time = @mget run_times; # Получить вектор результатов из MATLAB
Построим график, который покажет, какого ускорения перемножения матриц позволяет добиться использование Julia:
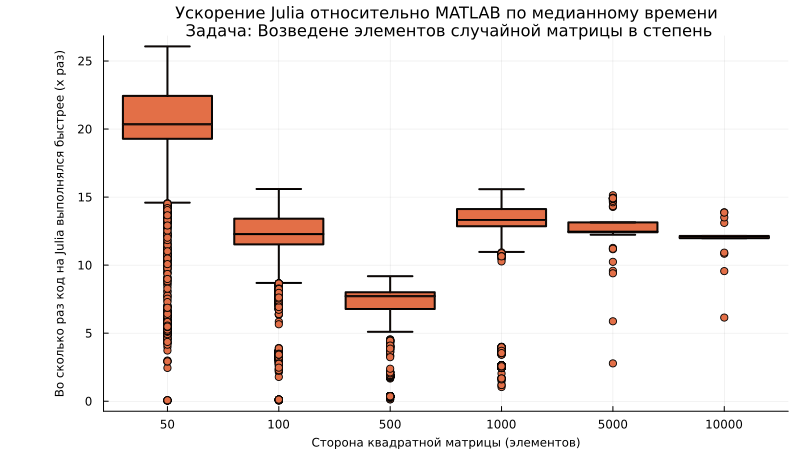
boxplot([matlab_time[i]./julia_times[i] for i in 1:length(sizes)], c=2, legend=false,
xlabel="Сторона квадратной матрицы (элементов)", ylabel="Во сколько раз код на Julia выполнялся быстрее (x раз)",
xticks=(1:length(sizes),sizes), lw=2, guidefont=font(8), titlefont=font(11),
title="Ускорение Julia относительно MATLAB по медианному времени\n Задача: Возведене элементов случайной матрицы в степень", left_margin=15Plots.mm, size=(800,450))
Задача матричного умножения
Аналогично предыдущим примерам выполним умножение матриц:
sizes = Int.([.5e2, 1e2, .5e3, 1e4, .5e5])
# Измерение в Julia
julia_times = []
for n in sizes
A = rand(n,n); B = rand(n,n);
result = @benchmark $A * $B;
append!(julia_times, [result.times ./ 1e9]) # ns to sec
end
@mput sizes # Передать параметры матриц в MATLAB
mat"""
run_times = [];
for i = 1:length(sizes)
n = sizes(i);
A = rand(n, n); B = rand(n, n); % Создаем случайные матрицы
testFunc = @() A * B; % Определяем функцию для тестирования
t = timeit(testFunc); % Измеряем время выполнения
run_times = [run_times, t]; % Сохраняем в выходной вектор
end
""";
matlab_time = @mget run_times; # Получить вектор результатов из MATLAB
boxplot([matlab_time[i]./julia_times[i] for i in 1:length(sizes)], c=3, legend=false,
xlabel="Сторона квадратной матрицы (элементов)", ylabel="Во сколько раз код на Julia выполнялся быстрее (x раз)",
xticks=(1:length(sizes),sizes), lw=2, guidefont=font(8), titlefont=font(11),
title="Ускорение Julia относительно MATLAB по медианному времени\n Задача: Возведене элементов случайной матрицы в степень", left_margin=15Plots.mm, size=(800,450))
Заключение
Кроме наглядных выводов, представленных на графиках, мы видим, как легко сравнивать выполнение функций в MATLAB и Julia и делать собственные выводы.
Поделитесь своим мнением – не испортили ли мы результаты тестирования каким-нибудь неоптимальным подходом, и предложите ваши варианты функций!