Cвёрточное кодирование
Сравнение эффективности систем связи с применением свёрточного кодирования и без него.
В данной статье представлен анализ улучшения характеристик достоверности передачи данных в цифровых системах связи при использовании свёрточного кодирования и алгоритма декодирования Витерби. Методология исследования основана на сравнительном моделировании двух систем: базовой некодированной системы QPSK и системы QPSK со свёрточным кодированием. Результаты моделирования, выраженные в виде кривых вероятности битовой ошибки (BER), наглядно демонстрируют значительный выигрыш в энергетической эффективности, достигаемый за счёт применения помехоустойчивого кодирования.
Одной из ключевых задач при проектировании систем связи является обеспечение высокой достоверности передачи информации в условиях воздействия шумов, помех и замираний. Количественной мерой надёжности системы служит вероятность битовой ошибки (BER — Bit Error Rate), определяемая как отношение числа ошибочно принятых битов к общему числу переданных. Зависимость BER от отношения сигнал-шум (SNR или Eb/N0) является фундаментальной характеристикой, позволяющей оценить необходимую мощность передатчика для достижения требуемого качества связи.
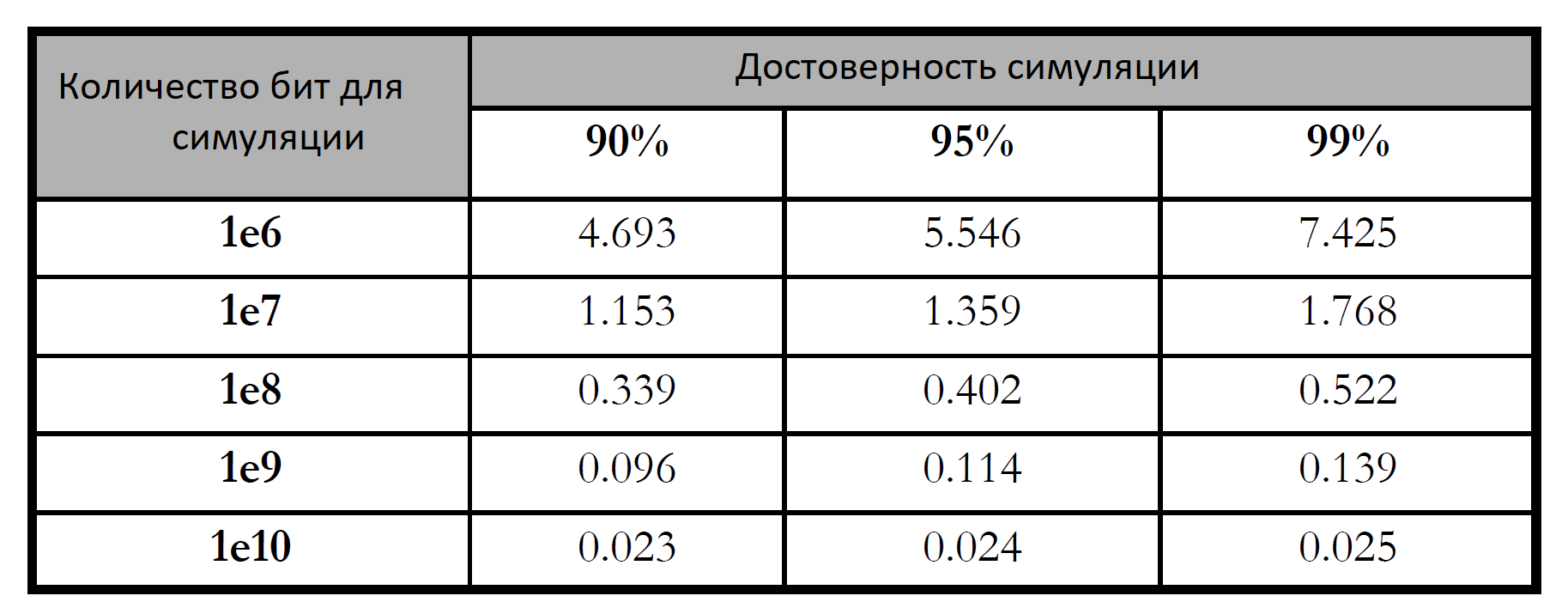
Прямое моделирование передачи больших объёмов данных является стандартным методом построения таких зависимостей. Для получения статистически значимых результатов, особенно при низких значениях BER (порядка 10^-6), требуется моделирование десятков или сотен миллионов бит. Это позволяет получить оценку с приемлемым доверительным интервалом.
В данной работе исследуется метод повышения помехоустойчивости — канальное свёрточное кодирование в сочетании с декодированием по алгоритму Витерби. Цель исследования — количественно оценить выигрыш в энергетике, который даёт применение данного типа кодирования в системе с модуляцией QPSK (Quadrature Phase-Shift Keying) в канале с аддитивным белым гауссовым шумом (AWGN).
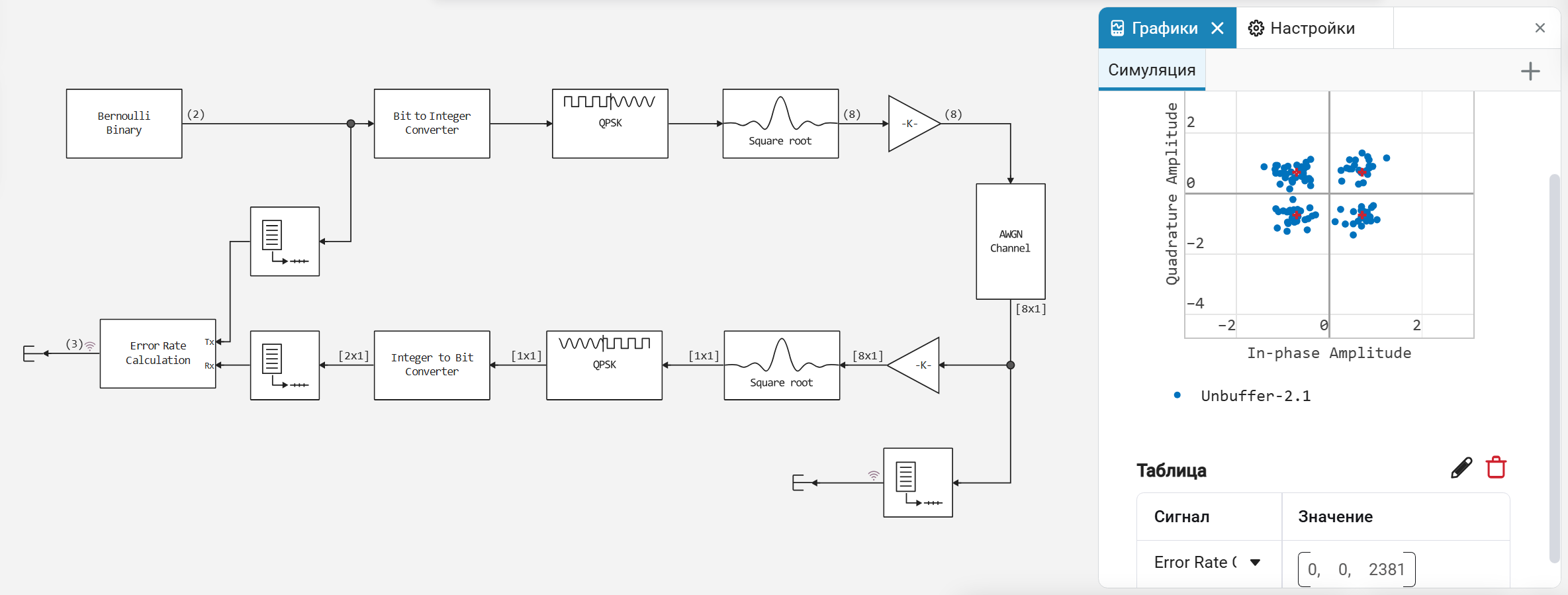
model = engee.load("qpsk_ber.engee");
EbNo_vec = 0:10;
EbNo = 0;
BER_vec = zeros(length(EbNo_vec))
for (i,EbNo1) in enumerate(EbNo_vec)
EbNo = EbNo1;
engee.run(model);
BER_vec[i] = [x[1] for x in collect(BER).value][end];
end
plot(EbNo_vec, BER_vec,
yaxis=:log10, # Логарифмическая шкала по оси Y
label="QPSK",
xlabel="EbNo (dB)",
ylabel="BER",
title="BER Кривая",
grid=true,
legend=:topright,
yticks=10.0.^(-5:1:0), # Добавляем тики от 1e-5 до 1
ylims=(1e-5, 1)) # Устанавливаем пределы оси Y
Далее представлена усовершенствованная схема, в которую добавлены блоки помехоустойчивого кодирования и декодирования. Информационные биты перед модуляцией проходят через свёрточный кодер, что увеличивает избыточность передаваемого потока. На приёмной стороне свёрточный декодер (Витерби) использует структуру решётки кода для исправления ошибок, возникших в канале. В данной модели использовалось жёсткое декодирование, а для сопоставления битов и фаз символов модулятора применялось отображение по коду Грея для минимизации ошибок при смежных символах.
Свёрточный кодер был задан с помощью функции poly2trellis, определяющей его структуру через длину кодового ограничения и порождающие полиномы. Важно отметить, что идентичная структура решётки была задана как для кодера, так и для декодера Витерби.
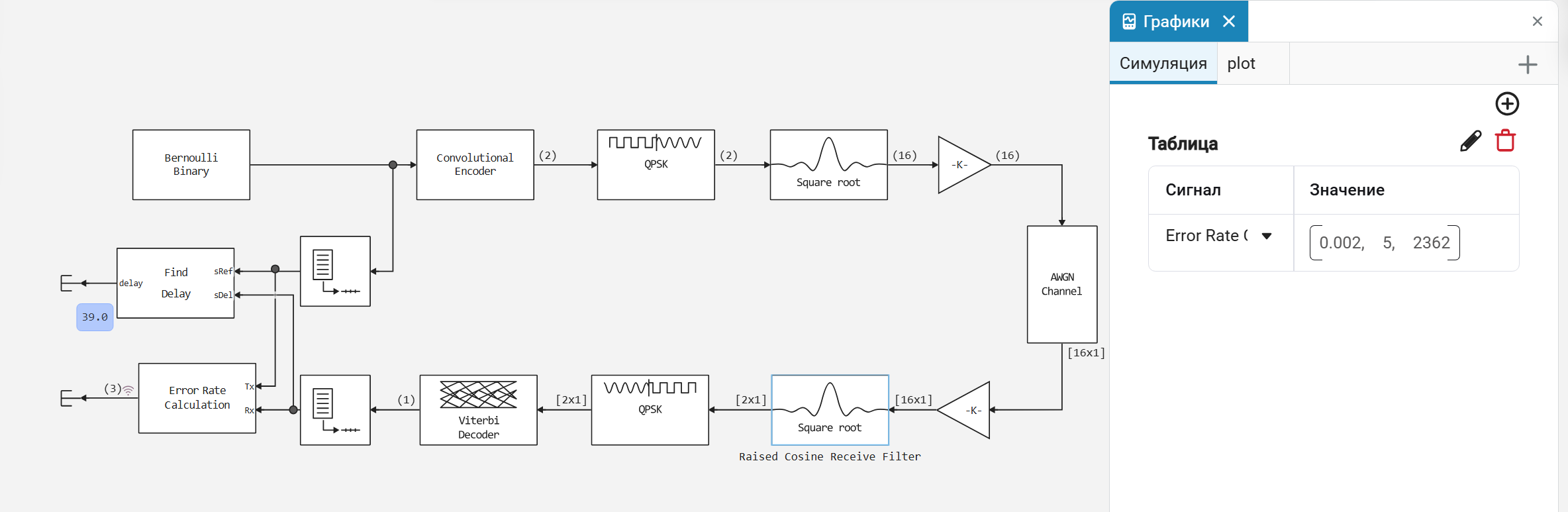
Для каждой из систем была построена кривая BER в зависимости от энергетического отношения Eb/N0 (в дБ). Диапазон Eb/N0 для некодированной системы составлял от 1 до 8 дБ, а для кодированной — от 1 до 6 дБ. Результаты представлены на совмещённом графике.
model_uncoded = engee.load("qpsk_ber.engee");
model_coded = engee.load("qpsk_coded_ber.engee");
EbNo_vec = 1:8;
BER_vec = zeros(length(EbNo_vec))
for (i,EbNo1) in enumerate(EbNo_vec)
EbNo = EbNo1;
engee.run(model_uncoded);
BER_vec[i] = [x[1] for x in collect(BER).value][end];
end
plot(EbNo_vec, BER_vec,
yaxis=:log10, # Логарифмическая шкала по оси Y
label="QPSK некодированная",
xlabel="EbNo (dB)",
ylabel="BER",
title="BER Кривая",
grid=true,
legend=:topright,
yticks=10.0.^(-5:1:0), # Добавляем тики от 1e-5 до 1
ylims=(1e-5, 1)) # Устанавливаем пределы оси Y
EbNo_vec = 1:6;
BER_vec = zeros(length(EbNo_vec))
for (i,EbNo1) in enumerate(EbNo_vec)
EbNo = EbNo1;
engee.run(model_coded);
BER_vec[i] = [x[1] for x in collect(BER).value][end];
end
plot!(EbNo_vec, BER_vec,
label="QPSK кодированная")
Анализ графиков позволяет сделать следующие выводы:
-
Некодированная система: Кривая BER для классической QPSK демонстрирует ожидаемую экспоненциальную зависимость. Для достижения BER на уровне 10^-4 требуется Eb/N0 около 6.5 дБ.
-
Кодированная система: Кривая BER для системы со свёрточным кодированием и декодированием Витерби расположена существенно ниже. Это означает, что для достижения того же значения BER (например, 10^-4) системе с кодированием требуется значительно меньшее отношение Eb/N0 — примерно на 3-4 дБ.
-
Кодировочный выигрыш: Разрыв между кривыми, наблюдаемый на графике, и является визуальным представлением кодировочного выигрыша (coding gain). На практике это означает, что система со свёрточным кодированием может либо работать с той же BER при меньшей мощности передатчика (экономия энергии), либо обеспечивать гораздо более высокую достоверность связи (меньшую BER) при той же мощности, что и некодированная система.
Вывод
Проведённое моделирование наглядно подтвердило высокую эффективность применения свёрточного кодирования в сочетании с алгоритмом Витерби для повышения помехоустойчивости цифровых систем связи.
Таким образом, использование свёрточных кодов и декодера Витерби является мощным и практически значимым инструментом при проектировании современных систем связи, где требования к энергоэффективности и достоверности передачи данных постоянно возрастают. Полученные кривые BER служат важным инструментом для системного инженера при расчёте бюджета линии связи и выборе параметров передачи.