Связь дифференциалов, производных и интегралов в Engee: от теории к практике

Математический анализ — фундамент для многих областей науки и инженерии. Производные и интегралы используются в физике, экономике, машинном обучении и даже игровом ИИ. Engee, благодаря своей производительности и удобному синтаксису, отлично подходит для численных вычислений.

В этой статье мы разберём:

Как вычислять производные и интегралы в Engee
Практическое применение в моделировании и оптимизации
Примеры из реальных проектов

1. Производные: от математики к коду

Производная функции ( f(x) ) показывает скорость её изменения. В Engee её можно вычислить аналитически (символьно) или численно.

1.1. Численное дифференцирование

Пакет FiniteDifferences позволяет вычислять производные методом конечных разностей:

Pkg.add("FiniteDifferences")

   Resolving package versions...
  No Changes to `~/.project/Project.toml`
  No Changes to `~/.project/Manifest.toml`

using FiniteDifferences

f(x) = x^2 + sin(x)
df = central_fdm(5, 1)(f, 1.0)  # Производная в точке x=1
println("f'(1) ≈ ", df)  # ≈ 2.5403 (точное значение: 2 + cos(1) ≈ 2.5403)

f'(1) ≈ 2.5403023058683987

Применение в реальных проектах:

В физике — расчёт ускорения (производная скорости).
В экономике — предельные издержки (производная функции затрат).

1.2. Автоматическое дифференцирование (AD)

Engee поддерживает автодифференцирование через ForwardDiff:

using ForwardDiff

f(x) = 3x^3 + 2x^2 + x
df_analytical(x) = ForwardDiff.derivative(f, x)

println("f'(2) = ", df_analytical(2))  # Выведет 45

f'(2) = 45

Где используется?

Оптимизация в машинном обучении (градиентный спуск).
Численное решение дифференциальных уравнений.

2. Интегралы: от суммирования до моделирования

Интеграл — это "площадь под кривой". В Engee его можно вычислить численно.

2.1. Численное интегрирование

Пакет QuadGK реализует метод Гаусса-Кронрода:

Pkg.add("QuadGK")

   Resolving package versions...
  No Changes to `~/.project/Project.toml`
  No Changes to `~/.project/Manifest.toml`

using QuadGK

f(x) = exp(-x^2)
integral, err = quadgk(f, 0, 1)
println("∫e^{-x²}dx ≈ ", integral)
println("Error estimate: ", err)

∫e^{-x²}dx ≈ 0.746824132812427
Error estimate: 7.887024366937112e-13

Примеры использования:

Финансы: расчёт дисконтированных денежных потоков.
Физика: вычисление работы силы.

2.2. Интегрирование ОДУ (дифференциальных уравнений)

Пакет DifferentialEquations.jl решает сложные динамические системы:

Pkg.add("DifferentialEquations")

using DifferentialEquations

# Модель хищник-жертва (Лотка-Вольтерра)
function lotka_volterra!(du, u, p, t)
    x, y = u
    α, β, δ, γ = p
    du[1] = α*x - β*x*y  # dx/dt
    du[2] = δ*x*y - γ*y  # dy/dt
end

u0 = [1.0, 1.0]          # Начальные условия: [жертвы, хищники]
tspan = (0.0, 10.0)       # Временной интервал
p = [1.5, 1.0, 1.0, 3.0] # Параметры модели

prob = ODEProblem(lotka_volterra!, u0, tspan, p)
sol = solve(prob, Tsit5())

using Plots
plot(sol, xlabel="Время", ylabel="Популяция", label=["Жертвы" "Хищники"])

Где применяется?

Биология: моделирование популяций.
Инженерия: расчёт динамики систем.

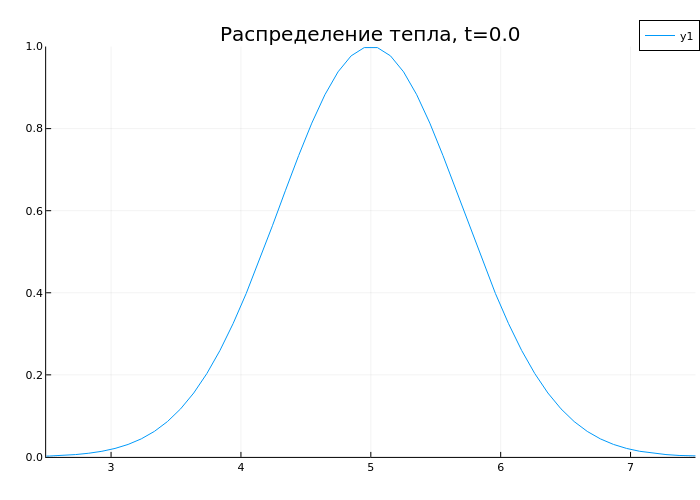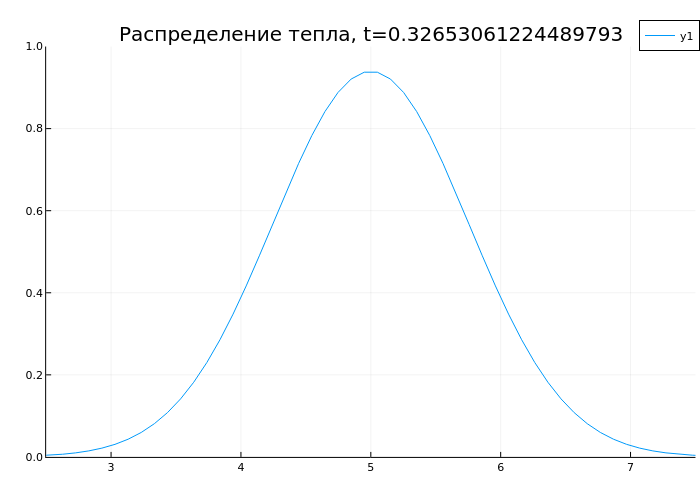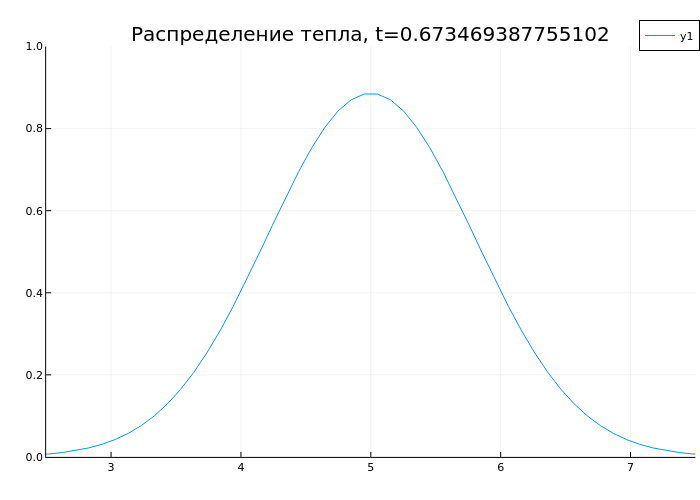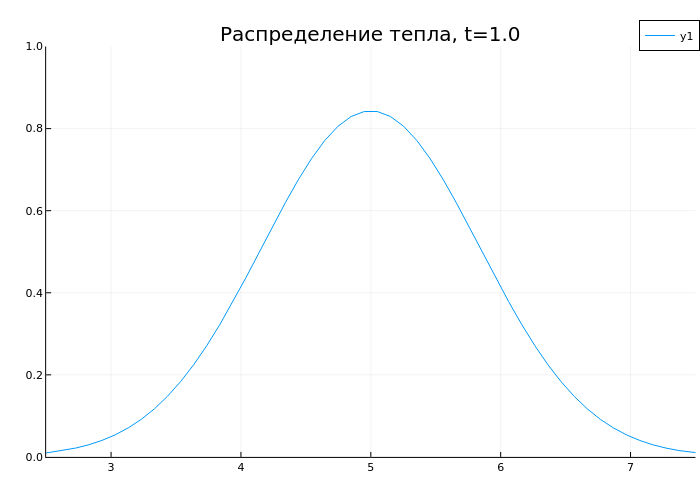
3. Связь производных и интегралов: уравнение теплопроводности

Рассмотрим уравнение теплопроводности:
∂T/∂t = a·∇²T + qᵥ/(c·ρ)

где:
a = λ/(cρ) — коэффициент температуропроводности [м²/с]
∇² — оператор Лапласа (∂²/∂x² + ∂²/∂y² + ∂²/∂z²)

Численное решение в Engee:

using DifferentialEquations

# Задаём сетку
L = 10.0
nx = 100
dx = L / nx
x = range(0, L, length=nx)

# Начальное условие (горячая середина)
u0 = exp.(-(x .- L/2).^2)

# Функция для правой части уравнения
function heat_equation!(du, u, p, t)
    α = p
    for i in 2:nx-1
        du[i] = α * (u[i+1] - 2u[i] + u[i-1]) / dx^2
    end
    du[1] = du[end] = 0  # Граничные условия
end

# Решаем
prob = ODEProblem(heat_equation!, u0, (0.0, 1.0), 0.1)
sol = solve(prob, Tsit5())

# Визуализация
anim = @animate for t in range(0, 1, length=50)
    plot(x, sol(t), ylims=(0,1), xlims=(2.5,7.5), title="Распределение тепла, t=$t")
end
gif(anim, "heat.gif", fps=10)

[ Info: Saved animation to /user/my_projects/Demo/heat.gif

Применение:

Физика: моделирование теплопередачи.
Финансы: расчёт опционов (уравнение Блэка-Шоулза).

Вывод

Engee предоставляет мощные инструменты для работы с производными и интегралами:

ForwardDiff — для градиентов и оптимизации.
QuadGK — для численного интегрирования.
DifferentialEquations.jl — для моделирования динамических систем.

Эти методы применяются в:

Физике (теплопередача, механика)
Экономике (оптимизация, прогнозирование)
Data Science (обучение моделей, диффузионные процессы)

Связь дифференциалов, производных и интегралов в Engee: от теории к практике

1. Производные: от математики к коду

1.1. Численное дифференцирование

1.2. Автоматическое дифференцирование (AD)

2. Интегралы: от суммирования до моделирования

2.1. Численное интегрирование

2.2. Интегрирование ОДУ (дифференциальных уравнений)

3. Связь производных и интегралов: уравнение теплопроводности

Вывод

Тип

Краткое описание

Связанные материалы

Теги

Категории

Языки

Форматы

Уровень

Статус

Опубликовано

Обновлено

Источник