Эффект Вентури
Модель эффекта Вентури
Повторим физический эксперимент, показывающий действие эффекта, благодаря которому работают старые карбюраторы, пульверизаторы, заправочные пистолеты, аэраторы, горелки и множество других устройств.
Описание модели
Изотермическая жидкость переходит из одного резервуара в другой, оба под атмосферным давлением. Граничные условия по обеим сторонам трубки задают насосы, перекачивающие заданный объем жидкости и задающие скорость.
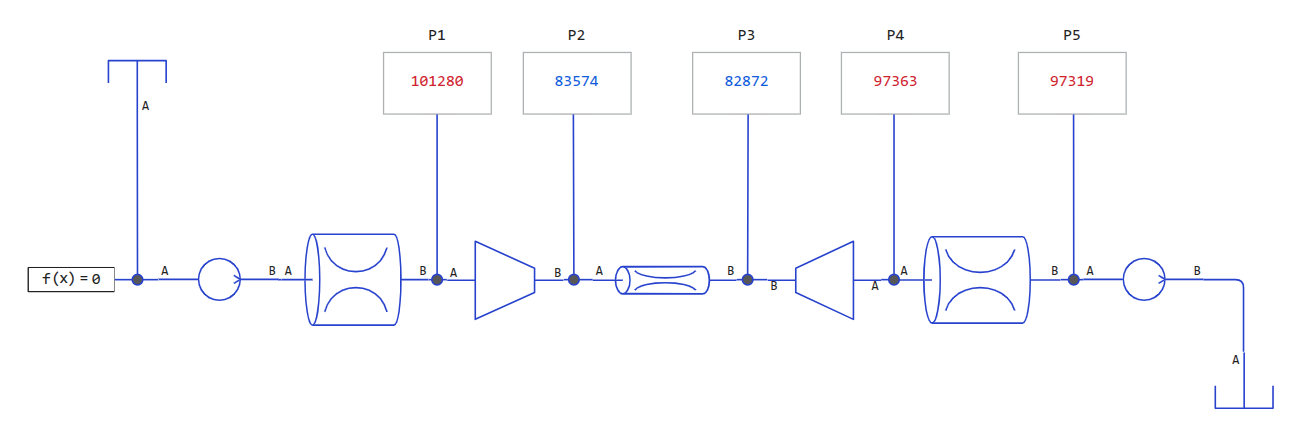
При диаметре на входе = 50 мм, и в узкой части = 25 мм, с учетом потерь в блоках сужения диаметра, стенки которых имеют наклон 10 градусов, мы наблюдаем следующие результаты симуляции:
-
давление на входе равно 101280 Па,
-
давление в горловине падает до 82872 Па,
-
после прохождения давление восстановилось до 97318 Па (потери около 4%).
Гидравлический диаметр каждого сечения приравнен к его геометрическому диаметру (поскольку трубы имеют круглое сечение), а суммарная длина местных сопротивлений приравнена к нулю, чтобы потери на трение в трубах минимально влияли на наблюдения.
По бокам от трубки находятся насосы постоянного объемного расхода, которые устанавливают ожидаемую скорость потока на входе и выходе.
Можно обойтись без насосов, но тогда нужно будет задать перепад давлений между резервуарами, и тогда входной и выходной конец трубки всегда будут показывать существенно разное давление.
Теоретические вычисления
Найдя площадь каждого сечения мы можем задать объемный расход насосов равный , где = 1.5 м/с — установленная нами скорость потока. Расход при равен = 1.5 · 3.1416 · (0.05)² / 4 = 0.002945 м³/с.
Площадь сечений вычисляется внутри соответствующих блоков, но выведем ее для наглядности:
= 0.002945 / 1.5 ≈ 0.001963 м²
= 3.1416 · (0.025)² / 4 ≈ 0.0004909 м²
Из уравнения неразрывности мы получаем скорость внутри узкого сегмента трубки, равную = 0.002945 / 0.0004909 ≈ 6.0 м/с.
Из уравнения Бернулли давление в горловине должно равняться:
= 101280 + 0.5 · 1000 · (1.5² - 6.0²) = 101280 + 500 · (2.25 - 36) = 101280 - 16875
≈ 84405 Па
Запуск модели
Примерно такие же данные мы получим, если запустим модель:
model = engee.open("venturi_effect_model.engee");
data = engee.run(model);
for k in sort(collect(keys(data)))
println(k, " = ", data[k].value[end])
end
В идеализированном эксперименте давление на выходе было бы равно давлению на входе, но в реальных системах, к которым приближена физическая модель, присутствуют гидравлические потери.
Мы отключили динамическую сжимаемость в трубах чтобы ускорить вычисления и подняли минимальный шаг локального решателя, поскольку работаем с изотермической жидкостью. Потери в 4000 Па можно объяснить трением и вихреобразованием в блоках сужающих диаметр.
Заключение
Мы показали, как при помощи физических блоков можно построить модель знаменитого физического эксперимента, показывающего действие эффекта Вентури, на котором основана работа множества приборов и агрегатов.