Flappy Bird AI
Flappy Bird AI: Эволюционное обучение нейронных сетей на Julia
Flappy Bird — культовая мобильная игра, которая стала идеальным полигоном для демонстрации принципов машинного обучения благодаря своей простоте и четким правилам. В этом проекте мы реализовали не только саму игру, но и две различные архитектуры нейронных сетей, которые обучаются играть в неё с помощью эволюционного алгоритма.
Ключевые особенности проекта:
- Полная реализация на стандартной библиотеке Julia без внешних зависимостей
- Символьная отрисовка игры в терминале
- Две архитектуры нейронных сетей: полносвязная(DenseNet) и сверточная (CNN)
- Генетический алгоритм для обучения
- Интерактивное меню для управления обучением и тестированием
Проект демонстрирует, как даже с использованием только базовых возможностей языка программирования можно создать полноценную систему машинного обучения. Flappy Bird была выбрана не случайно — это идеальный тестовый стенд:
- Простые правила, но сложное мастерство
- Четкая система наград (очки за пролет через трубы)
- Дискретные действия (прыжок или нет)
- Визуально понятный прогресс обучения
Использование символьной графики в командной строке показывает, что для демонстрации концепций машинного обучения не нужны сложные графические библиотеки — важны сами алгоритмы и принципы.
Технологический стек:
- Julia как высокопроизводительный язык для научных вычислений
- Генетические алгоритмы как метод оптимизации без градиентов
- Нейронные сети как универсальные аппроксиматоры
- Консольный интерфейс для максимальной портативности
Этот проект нацелен, показывая "изнутри" как работают нейронные сети и эволюционные алгоритмы, без магии фреймворков глубокого обучения.
Теперь перейдём к самой реализации проекта. В основе реализации Flappy Bird лежат две ключевые структуры данных, которые инкапсулируют состояние всех игровых объектов, и набор глобальных параметров, определяющих физику и баланс игры. Этот минималистичный подход характерен для игровых движков, где четкое разделение данных и логики обеспечивает предсказуемость и простоту отладки.
Объект Bird представляет собой управляемую птицу — главного героя игры. В его полях хранится полное динамическое состояние: вертикальная позиция y (дробное число для плавности), скорость v (положительная вниз, отрицательная вверх), текущий счет s (целое число пройденных труб) и булевый флаг активности a, указывающий, жива ли птица. Этих четырех параметров достаточно для описания всей механики движения птицы — её реакция на гравитацию, импульс прыжка и взаимодействие с границами.
Каждая труба представлена структурой Pipe, содержащей три параметра: горизонтальную координату x (отслеживает положение трубы относительно птицы), вертикальную позицию прохода gy (определяет, где находится безопасный промежуток) и флаг пройденности p (исключает повторное начисление очков). Трубы движутся навстречу птице, создавая основной игровой вызов — необходимость точно пролетать через узкие промежутки.
Массив GP содержит семь числовых констант, которые задают геометрию и физику игрового мира. Это ширина и высота поля, сила гравитации и прыжка, размеры труб, а также скорость их движения. Такая централизованная конфигурация позволяет легко балансировать сложность игры и экспериментировать с параметрами, не затрагивая основную логику.
Функция init_game создает стартовое состояние, возвращая птицу в центре экрана с нулевой скоростью и пустым списком труб. Эта простая процедура обеспечивает воспроизводимость каждого игрового эпизода, что критически важно для процесса обучения — нейронная сеть должна учиться на последовательных, детерминированных примерах.
Вместе эти компоненты образуют компактную, но полную модель игры, где каждый параметр имеет четкую роль, а взаимодействие объектов описывается минимальным набором правил.
mutable struct Bird
y::Float64
v::Float64
s::Int
a::Bool
end
mutable struct Pipe
x::Float64
gy::Int
p::Bool
end
const GP = [40.0, 15.0, 0.4, -2.0, 4.0, 6.0, 1.2]
function init_game()
Bird(GP[2] ÷ 2, 0.0, 0, true), Pipe[]
end
Функция update_bird! реализует физику движения птицы, обрабатывая два ключевых воздействия: гравитацию и прыжки. Каждый игровой кадр птица получает либо импульс вверх при прыжке, либо дополнительное ускорение вниз от гравитации, что создает характерную "прыгающую" механику, аналогичную оригинальной игре.
Сначала обновляется вертикальная скорость: если передан сигнал jump, скорость устанавливается равной силе прыжка (отрицательное значение для движения вверх), иначе к текущей скорости добавляется гравитация. Затем позиция птицы изменяется на величину скорости, создавая плавное перемещение.
Далее функция проверяет границы игрового поля. Если птица опускается ниже нижней границы, её позиция фиксируется на минимальном значении, а скорость сбрасывается, предотвращая выход за пределы экрана. Если же птица поднимается выше верхней границы, это считается поражением — флаг активности устанавливается в false, что завершит игровой эпизод. Эти проверки обеспечивают корректное поведение птицы в ограниченном пространстве.
function update_bird!(b, jump)
b.v = jump ? GP[4] : b.v + GP[3]
b.y += b.v
if b.y < 1
b.y = 1; b.v = 0
elseif b.y > GP[2]
b.a = false
end
end
Функция update_pipes! отвечает за жизненный цикл препятствий — их движение, взаимодействие с игроком и генерацию новых труб. Это ключевой механизм, создающий непрерывный игровой процесс и систему начисления очков.
Сначала функция удаляет трубы, которые полностью ушли за левую границу экрана. Это поддерживает массив pipes в актуальном состоянии, удаляя объекты, более не участвующие в игре. Затем для каждой оставшейся трубы происходит смещение влево с постоянной скоростью, создавая иллюзию движения птицы вперед. Одновременно проверяется, прошла ли птица через трубу — если труба пересекла контрольную точку и ранее не была засчитана, счет игрока увеличивается, а труба помечается как пройденная.
Генерация новых труб происходит по принципу поддержания постоянного потока препятствий. Если труб нет или последняя труба достаточно далеко продвинулась, создается новая труба в правой части экрана. Её вертикальное положение прохода случайно выбирается в допустимом диапазоне, обеспечивая разнообразие траекторий. Этот механизм гарантирует бесконечный и непредсказуемый геймплей, необходимый для обучения адаптивному поведению.
function update_pipes!(pipes, b)
filter!(p -> p.x > -GP[5], pipes)
for p in pipes
p.x -= GP[7]
if !p.p && p.x < 5
p.p = true
b.s += 1
end
end
if isempty(pipes) || pipes[end].x < GP[1] - 20
push!(pipes, Pipe(GP[1], rand(4:Int(GP[2]) - Int(GP[6]) - 2), false))
end
end
Функция check_collision реализует детектирование столкновений птицы с трубами — ключевой механизм определения успешности игры. Алгоритм проверяет, находится ли птица в зоне столкновения с любой из активных труб, и завершает игру при обнаружении касания.
Сначала позиция птицы округляется до целого числа для упрощения расчетов, что соответствует дискретной сетке отрисовки в терминале. Затем для каждой трубы проверяется горизонтальное перекрытие: если птица (находящаяся на фиксированной горизонтальной позиции 5) находится в пределах ширины трубы, запускается проверка вертикального столкновения.
Вертикальная проверка определяет, попала ли птица в безопасный промежуток между трубами. Если вертикальная позиция птицы находится выше верхней трубы или ниже нижней, фиксируется столкновение. В этом случае флаг активности птицы устанавливается в false, что немедленно завершает игровой цикл. Функция возвращает управление досрочно, так как дальнейшие проверки после столкновения не требуются.
function check_collision(b, pipes)
by = round(Int, b.y)
for p in pipes
if 5 >= p.x && 5 <= p.x + GP[5] - 1
if by < p.gy || by > p.gy + GP[6] - 1
b.a = false
return
end
end
end
end
Функция extract_state выполняет критически важную задачу преобразования игрового состояния в формат, пригодный для обработки нейронной сетью. Она реализует два принципиально разных подхода к представлению данных, соответствующих двум типам нейросетевых архитектур.
Алгоритм начинается с поиска ближайшей непройденной трубы, которая еще не была пройдена птицей и находится перед ней. Если такой трубы нет (в начале игры или после всех труб), возвращается состояние по умолчанию: либо нулевой вектор для полносвязной сети, либо карта с птицей в центре для сверточной.
Для сверточной сети (state_type == :conv) создается двумерная матрица размером с игровое поле, представляющая собой своеобразную "карту видимости". Позиция птицы отмечается значением 1.0, а трубы — значением 0.5 в тех клетках, где они занимают пространство. Такой растровый подход позволяет сверточной сети самостоятельно выявлять пространственные паттерны и отношения между объектами.
Для полносвязной сети (state_type == :basic) формируется компактный вектор из пяти нормализованных признаков: относительная вертикальная позиция птицы, её скорость (ограниченная диапазоном [-1, 1]), относительное горизонтальное расстояние до ближайшей трубы, а также верхняя и нижняя границы безопасного прохода. Эта representation извлекает наиболее релевантные для принятия решения параметры, предоставляя сети уже подготовленные высокоуровневые признаки.
Ключевым аспектом является нормализация всех значений к диапазону около [0, 1] или [-1, 1], что ускоряет и стабилизирует обучение нейронных сетей, предотвращая проблемы с градиентами и обеспечивая сходимость алгоритмов оптимизации.
function extract_state(b, pipes, state_type=:basic)
closest = nothing
for p in pipes
if !p.p && p.x + GP[5] >= 5
closest = p
break
end
end
if closest === nothing
if state_type == :conv
state = zeros(Float64, Int(GP[2]), Int(GP[1]))
state[Int(GP[2])÷2, 5] = 1.0
return state
else
return zeros(Float64, 5)
end
end
if state_type == :conv
state = zeros(Float64, Int(GP[2]), Int(GP[1]))
by = clamp(round(Int, b.y), 1, Int(GP[2]))
state[by, 5] = 1.0
for p in pipes
px = round(Int, p.x)
start_x = max(1, px)
end_x = min(Int(GP[1]), px + Int(GP[5]) - 1)
if start_x <= end_x
for x in start_x:end_x
for y in 1:Int(GP[2])
if y < p.gy || y > p.gy + Int(GP[6]) - 1
state[y, x] = 0.5
end
end
end
end
end
return state
else
return [
b.y / GP[2],
clamp(b.v / 5.0, -1.0, 1.0),
(closest.x - 5) / GP[1],
closest.gy / GP[2],
(closest.gy + GP[6]) / GP[2]
]
end
end
run_episode() — это центральная функция, которая выполняет полный цикл игры для оценки нейронной сети. Она инкапсулирует логику взаимодействия между игровой средой и ИИ-агентом.
Функция начинается с инициализации нового игрового состояния — создания птицы и пустого списка труб. Затем запускается основной игровой цикл, который продолжается до тех пор, пока птица жива и не превышен лимит шагов, такой подход предотвращает бесконечные игры. На каждом шаге извлекается текущее состояние игры в формате, соответствующем архитектуре сети (basic для полносвязной или conv для сверточной).
Нейронная сеть получает это состояние и возвращает вероятность прыжка. Пороговое значение 0.5 преобразует непрерывную вероятность в бинарное решение: true для прыжка, false для продолжения падения. Это действие применяется к птице, обновляются позиции труб и проверяются столкновения.
Если включен режим отрисовки (render=true), на каждом шаге выводится графическое представление игры в терминале с небольшой задержкой для удобства наблюдения. По завершению функция возвращает финальный счет — количество успешно пройденных труб, который служит оценкой эффективности нейронной сети.
function run_episode(network, state_type=:basic; render=false, max_steps=1000)
bird, pipes = init_game()
step = 0
while bird.a && step < max_steps
state = extract_state(bird, pipes, state_type)
if state_type == :conv
action = conv_forward(network, state) > 0.5
else
action = dense_forward(network, state) > 0.5
end
update_bird!(bird, action)
update_pipes!(pipes, bird)
check_collision(bird, pipes)
if render
draw(bird, pipes)
sleep(0.1)
end
step += 1
end
return bird.s
end
draw() реализует консольную графику для визуализации игрового процесса. Эта функция использует только стандартные возможности терминала для создания псевдографического интерфейса, демонстрируя, что даже без специализированных библиотек можно создать наглядное представление игры.
Основной цикл проходит по каждой строке игрового поля высотой h. Для каждой строки выводится левая граница "|", затем проверяется, находится ли птица на этой высоте — если да, выводится эмодзи "🤖", иначе пробел. Далее для каждой внутренней колонки (кроме граничных областей) проверяется, не находится ли эта позиция внутри трубы. Если да и позиция не попадает в безопасный промежуток между трубами, выводится символ "█", представляющий препятствие.
После отрисовки всего поля выводится нижняя граница и статус игры. Если птица погибла, выводится сообщение о завершении игры с эмодзи "💀" и финальным счетом.
function draw(b, pipes)
print("\033[2J\033[H")
w, h = Int(GP[1]), Int(GP[2])
println("="^w)
println("FLAPPY BIRD AI | Счет: $(b.s)")
println("="^w)
for y in 1:h
print("|")
print(y == round(Int, b.y) ? "🤖" : " ")
for x in 7:w-2
is_pipe = false
for p in pipes
px = round(Int, p.x)
if x >= px && x < px + Int(GP[5])
if y < p.gy || y > p.gy + Int(GP[6]) - 1
print("█")
is_pipe = true
break
end
end
end
!is_pipe && print(" ")
end
println("|")
end
println("="^w)
println("ТЕСТОВЫЙ ПРОГОН")
!b.a && println("\n💀 Игра окончена! Счет: $(b.s)")
end
В проекте реализованы две архитектуры нейронных сетей, каждая представлена своей структурой данных. Эти структуры инкапсулируют все обучаемые параметры сетей, что позволяет эффективно манипулировать ими в ходе эволюционного обучения.
mutable struct DenseNet описывает полносвязную нейронную сеть с одним скрытым слоем. Она содержит матрицу весов w1 размером 8×5 для связи между входным и скрытым слоем, вектор смещений b1 для скрытого слоя, матрицу весов w2 размером 1×8 для связи между скрытым и выходным слоем, и скалярное смещение b2 для выходного нейрона. Такая структура отражает классическую архитектуру многослойного перцептрона.
mutable struct ConvNet представляет сверточную сеть. Она включает четырехмерный массив conv_weights для ядер свертки (3×3×1×4, где 4 — количество фильтров), вектор смещений conv_bias для сверточного слоя, матрицу fc_weights для полносвязного слоя и вектор fc_bias для его смещений. Эта структура поддерживает современный подход к обработке изображений.
mutable struct DenseNet
w1::Matrix{Float64}
b1::Vector{Float64}
w2::Matrix{Float64}
b2::Vector{Float64}
end
mutable struct ConvNet
conv_weights::Array{Float64,4}
conv_bias::Vector{Float64}
fc_weights::Matrix{Float64}
fc_bias::Vector{Float64}
end
function init_dense()
DenseNet(
randn(8, 5) * 0.1,
zeros(8),
randn(1, 8) * 0.1,
zeros(1)
)
end
function init_conv()
height, width = 15, 40
filters = 4
conv_size = (height - 2) * (width - 2) * filters
ConvNet(
randn(3, 3, 1, filters) * 0.1,
zeros(filters),
randn(1, conv_size) * 0.1,
zeros(1)
)
end
dense_forward() и conv_forward() реализуют прямое распространение для двух различных архитектур нейронных сетей. Эти функции являются вычислительным ядром системы, преобразуя игровое состояние в решение о действии.
Полносвязная сеть (dense_forward) работает с компактным вектором из пяти признаков. Она выполняет линейное преобразование через веса w1, добавляет смещения b1, применяет нелинейность tanh для скрытого слоя, затем делает второе линейное преобразование через w2 и b2, и наконец преобразует результат в вероятность через сигмоиду. Эта двухслойная архитектура эффективна для обработки небольшого числа высокоуровневых признаков.
Сверточная сеть (conv_forward) обрабатывает двумерную матрицу состояния игры. Она выполняет операцию свертки, применяя несколько фильтров 3×3 ко всем возможным позициям на карте с помощью вложенных циклов. Для каждого фильтра вычисляется скалярное произведение между ядром фильтра и соответствующим участком входного изображения, добавляется смещение, и применяется функция активации ReLU (max(..., 0.0)). Результаты свертки затем "разворачиваются" в одномерный вектор и пропускаются через полносвязный слой с сигмоидной активацией на выходе.
Ключевое различие между подходами: полносвязная сеть получает предобработанные высокоуровневые признаки (позиция, скорость, расстояние до труб), тогда как сверточная работает с "сырыми" пикселями игрового поля и самостоятельно обучается выделять релевантные паттерны. Обе функции возвращают вероятность прыжка в диапазоне (0, 1), которая затем пороговым значением 0.5 преобразуется в бинарное решение.
function dense_forward(net::DenseNet, state)
h = tanh.(net.w1 * state .+ net.b1)
logits = net.w2 * h .+ net.b2
return 1.0 / (1.0 + exp(-logits[1]))
end
function conv_forward(net::ConvNet, state)
height, width = size(state)
filters = size(net.conv_weights, 4)
conv_out = zeros(Float64, height-2, width-2, filters)
for f in 1:filters
for i in 1:height-2
for j in 1:width-2
sum_val = 0.0
for ki in 1:3
for kj in 1:3
row = i + ki - 1
col = j + kj - 1
if row <= height && col <= width
sum_val += state[row, col] * net.conv_weights[ki, kj, 1, f]
end
end
end
conv_out[i, j, f] = max(sum_val + net.conv_bias[f], 0.0)
end
end
end
flattened = vec(conv_out)
logits = net.fc_weights * flattened .+ net.fc_bias
return 1.0 / (1.0 + exp(-logits[1]))
end
evaluate_network() выполняет оценку производительности нейронной сети в игровой среде. Эта функция служит фитнес-функцией в эволюционном алгоритме, количественно измеряя, насколько хорошо сеть играет в Flappy Bird.
Функция запускает несколько независимых игровых эпизодов (по умолчанию 3) с отключенной отрисовкой для максимальной скорости вычислений. Для каждого эпизода она вызывает run_episode, которая возвращает финальный счет — количество успешно пройденных труб. Все счеты суммируются, и возвращается их среднее арифметическое.
Использование нескольких эпизодов вместо одного повышает надежность оценки, сглаживая влияние случайных факторов, таких как начальное расположение труб. Три эпизода обеспечивают баланс между точностью оценки и вычислительными затратами, что важно при оценке сотен сетей в каждом поколении эволюционного алгоритма.
Параметр state_type позволяет функции работать с обеими архитектурами сетей — передается в run_episode для корректного формата входных данных. Возвращаемое среднее значение служит объективной мерой приспособленности (fitness) сети, на основе которой происходит отбор и размножение в генетическом алгоритме.
function evaluate_network(network, state_type=:basic, episodes=3)
total = 0.0
for _ in 1:episodes
score = run_episode(network, state_type; render=false)
total += score
end
return total / episodes
end
train_genetic!() реализует генетический алгоритм для обучения популяции нейронных сетей. Это ядро системы машинного обучения, имитирующее естественный отбор для постепенного улучшения игровых навыков сетей.
Алгоритм работает в поколениях. Каждое поколение начинается с оценки всех сетей в популяции с помощью evaluate_network. Сохраняются три ключевые метрики: лучший, средний и худший результаты, которые выводятся для отслеживания прогресса. Лучшая сеть сохраняется отдельно как потенциальное решение.
Если лучшая сеть поколения превосходит целевой счет target_score, обучение завершается досрочно — цель достигнута. В противном случае происходит отбор наиболее приспособленных особей: верхние 25% сетей (элита) отбираются для создания следующего поколения. Размер элиты гарантированно не меньше одной сети даже в маленьких популяциях.
Создание нового поколения использует стратегию "элитизма с мутацией". Все элитные сети сохраняются в следующем поколении без изменений (элитизм). Остальные места заполняются потомками, созданными путем клонирования случайно выбранной элитной особи с последующей возможной мутацией.
Мутация происходит с вероятностью mutation_rate (по умолчанию 30%) и добавляет небольшие случайные изменения из нормального распределения к параметрам сети. Эти изменения имитируют генетические мутации, вводя разнообразие и позволяя исследовать новые стратегии. Коэффициент 0.1 ограничивает размер мутаций, предотвращая разрушительные изменения.
Цикл повторяется до достижения максимального числа поколений или целевого счета. Функция возвращает финальную популяцию, статистику по всем поколениям, лучшую найденную сеть и её счет. Такой эволюционный подход не требует градиентов или обратного распространения ошибки, делая обучение доступным для демонстрации базовых принципов искусственного интеллекта.
function train_genetic!(population, state_type=:basic; target_score=20, max_generations=100, mutation_rate=0.3)
results = []
best_score = 0.0
best_network = nothing
for generation in 1:max_generations
scores = [evaluate_network(net, state_type) for net in population]
gen_best = maximum(scores)
gen_avg = sum(scores) / length(scores)
gen_worst = minimum(scores)
push!(results, (generation, gen_best, gen_avg, gen_worst))
println("Поколение $generation | Лучший: ", round(gen_best, digits=2), " | Средний: ", round(gen_avg, digits=2), " | Худший: ", round(gen_worst, digits=2))
if gen_best > best_score
best_score = gen_best
best_idx = argmax(scores)
best_network = deepcopy(population[best_idx])
end
if gen_best >= target_score
println("✓ Достигнут целевой счет $target_score")
break
end
sorted_idx = sortperm(scores, rev=true)
elite_size = max(1, length(population) ÷ 4)
elites = population[sorted_idx[1:elite_size]]
new_pop = deepcopy(elites)
while length(new_pop) < length(population)
parent = rand(elites)
if state_type == :conv
child = ConvNet(
copy(parent.conv_weights),
copy(parent.conv_bias),
copy(parent.fc_weights),
copy(parent.fc_bias)
)
if rand() < mutation_rate
child.conv_weights .+= randn(size(child.conv_weights)...) * 0.1
child.conv_bias .+= randn(size(child.conv_bias)...) * 0.1
child.fc_weights .+= randn(size(child.fc_weights)...) * 0.1
child.fc_bias .+= randn(size(child.fc_bias)...) * 0.1
end
else
child = DenseNet(
copy(parent.w1),
copy(parent.b1),
copy(parent.w2),
copy(parent.b2)
)
if rand() < mutation_rate
child.w1 .+= randn(size(child.w1)...) * 0.1
child.b1 .+= randn(size(child.b1)...) * 0.1
child.w2 .+= randn(size(child.w2)...) * 0.1
child.b2 .+= randn(size(child.b2)...) * 0.1
end
end
push!(new_pop, child)
end
population = new_pop[1:length(population)]
end
return population, results, best_network, best_score
end
function argmax(x)
max_val = -Inf
max_idx = 1
for (i, val) in enumerate(x)
if val > max_val
max_val = val
max_idx = i
end
end
return max_idx
end
struct NetworkResult представляет собой контейнер для хранения полной информации об обученной нейронной сети и процессе её обучения. Эта структура обеспечивает систематизированное хранение и сравнение различных моделей, обученных в рамках проекта.
network хранит саму обученную нейронную сеть — экземпляр DenseNet или ConvNet, содержащий все обученные веса и смещения. state_type указывает, какой тип входных данных использует сеть (:basic для вектора признаков или :conv для матрицы состояния), что важно при использовании сети для игры.
test_score содержит финальную оценку производительности сети, усредненную по нескольким тестовым эпизодам. Это объективный показатель качества обучения. training_stats хранит подробную статистику по всем поколениям обучения — динамику лучшего, среднего и худшего результатов, позволяя анализировать процесс сходимости алгоритма.
params указывает общее количество обучаемых параметров сети, что дает представление о сложности модели и вычислительных требованиях. Вместе эти поля образуют полный "паспорт" обученной сети, позволяющий воспроизводить эксперименты, сравнивать разные подходы и демонстрировать результаты.
struct NetworkResult
name::String
architecture::String
network::Any
state_type::Symbol
test_score::Float64
training_stats::Vector{Any}
params::Int
end
Представленный ниже код реализует полную интерактивную систему для обучения, тестирования и сравнения нейронных сетей в рамках проекта Flappy Bird AI. Система построена вокруг нескольких специализированных меню, каждое из которых отвечает за определенный этап рабочего процесса.
Главное меню (main_menu) служит центральным хабом, отображая список всех обученных сетей и предоставляя доступ к основным функциям программы. Оно поддерживает накопление результатов между сессиями, позволяя обучать несколько сетей и сравнивать их между собой.
Меню обучения полносвязной сети (train_dense_menu) и меню обучения сверточной сети (train_conv_menu) имеют схожую структуру, но настраиваются под особенности каждой архитектуры. Оба меню запрашивают у пользователя параметры обучения: имя сети, размер популяции, количество поколений, целевой счет и число тестовых эпизодов. После сбора параметров они запускают эволюционный алгоритм обучения и сохраняют результаты в общий список. Различия заключаются в описании архитектуры и расчете количества параметров.
Меню тестирования (testing_menu) позволяет выбрать любую обученную сеть для визуальной демонстрации её игры. Оно включает защиту от некорректного ввода, предупреждение о возможности прерывания демонстрации и обработку исключений для устойчивой работы.
Функция сравнения результатов (compare_results) ранжирует все обученные сети по тестовому счету, используя эмодзи для награждения первых трех мест. Она также показывает статистику обучения лучшей сети, демонстрируя прогресс от начального к финальному результату.
Все меню используют единообразное оформление с очисткой экрана, разделителями и информативными заголовками, создавая профессиональный пользовательский опыт исключительно средствами консоли. Система демонстрирует, как сложный процесс машинного обучения можно сделать доступным и интуитивно понятным через хорошо структурированный текстовый интерфейс.
function main_menu()
results = NetworkResult[]
while true
print("\033[2J\033[H")
println("="^60)
println(" FLAPPY BIRD - ЭВОЛЮЦИОННЫЙ АЛГОРИТМ")
println("="^60)
if !isempty(results)
println("\nОБУЧЕННЫЕ СЕТИ:")
for (i, r) in enumerate(results)
println("$i. $(r.name) ($(r.architecture)): ", round(r.test_score, digits=2), " | Параметров: $(r.params)")
end
end
println("\n" * "-"^60)
println("МЕНЮ ОБУЧЕНИЯ:")
println("1. Обучить Полносвязную сеть")
println("2. Обучить Сверточную сеть (CNN)")
println("3. Тестовый прогон с графикой")
println("4. Сравнить все обученные сети")
println("5. Выход")
println("-"^60)
print("\nВыбор: ")
choice = readline()
if choice == "1"
results = train_dense_menu(results)
elseif choice == "2"
results = train_conv_menu(results)
elseif choice == "3"
testing_menu(results)
elseif choice == "4"
compare_results(results)
elseif choice == "5"
println("Выход")
return
end
end
end
function train_dense_menu(results)
print("\033[2J\033[H")
println("="^60)
println("ОБУЧЕНИЕ ПОЛНОСВЯЗНОЙ СЕТИ (Эволюционный алгоритм)")
println("="^60)
println("\nАрхитектура сети:")
println("Входной слой: 5 нейронов (позиция, скорость, дистанция до трубы)")
println("Скрытый слой: 8 нейронов с функцией активации tanh")
println("Выходной слой: 1 нейрон с сигмоидой (вероятность прыжка)")
println("Всего параметров: 5×8 + 8 + 8×1 + 1 = 57")
print("\nВведите имя для сети: ")
name = readline()
print("Количество сетей в популяции: ")
pop_size = parse(Int, readline())
print("Максимальное количество поколений: ")
max_generations = parse(Int, readline())
print("Целевой счет для остановки: ")
target_score = parse(Float64, readline())
print("Тестовых эпизодов после обучения: ")
test_episodes = parse(Int, readline())
println("\nСоздание популяции...")
population = [init_dense() for _ in 1:pop_size]
println("Начало эволюционного обучения...")
println("Цель: достичь счета $target_score")
println("-"^60)
final_pop, training_stats, best_net, best_score = train_genetic!(
population, :basic,
target_score=target_score,
max_generations=max_generations,
mutation_rate=0.3
)
println("\nТестовый прогон лучшей сети...")
test_score = evaluate_network(best_net, :basic, test_episodes)
push!(results, NetworkResult(
name,
"Полносвязная (5-8-1)",
best_net,
:basic,
test_score,
training_stats,
57
))
println("\nОбучение завершено!")
println("Лучший счет в обучении: ", round(best_score, digits=2))
println("Тестовый счет: ", round(test_score, digits=2))
println("Нажмите Enter для продолжения...")
readline()
return results
end
function testing_menu(results)
if isempty(results)
println("Нет обученных сетей!")
sleep(2)
return
end
while true
print("\033[2J\033[H")
println("="^60)
println("ТЕСТОВЫЙ ПРОГОН С ГРАФИКОЙ")
println("="^60)
println("\nВыберите сеть для тестирования (0 для выхода):")
for (i, r) in enumerate(results)
println("$i. $(r.name) ($(r.architecture)): ", round(r.test_score, digits=2))
end
print("\nНомер сети: ")
input = readline()
if input == "0"
return
end
idx = tryparse(Int, input)
if idx === nothing || idx < 1 || idx > length(results)
println("Неверный номер!")
sleep(2)
continue
end
chosen = results[idx]
println("\nЗапуск демонстрации сети '$(chosen.name)'...")
println("Нажмите Ctrl+C для выхода из демо")
println("Запуск через 3 секунды...")
sleep(3)
try
score = run_episode(chosen.network, chosen.state_type; render=true, max_steps=1000)
println("\nДемонстрация завершена! Счет: $score")
catch e
if !(e isa InterruptException)
println("\nОшибка при выполнении: $e")
end
end
println("\nНажмите Enter для продолжения...")
readline()
end
end
function train_conv_menu(results)
print("\033[2J\033[H")
println("="^60)
println("ОБУЧЕНИЕ СВЕРТОЧНОЙ СЕТИ (CNN) - Эволюционный алгоритм")
println("="^60)
println("\nАрхитектура сети:")
println("Вход: 15×40 (высота×ширина игрового поля)")
println("Сверточный слой: 4 фильтра 3×3, ReLU активация")
println("Полносвязный слой: 1 нейрон с сигмоидой")
println("Всего параметров: ~500")
print("\nВведите имя для сети: ")
name = readline()
print("Количество сетей в популяции: ")
pop_size = parse(Int, readline())
print("Максимальное количество поколений: ")
max_generations = parse(Int, readline())
print("Целевой счет для остановки: ")
target_score = parse(Float64, readline())
print("Тестовых эпизодов после обучения: ")
test_episodes = parse(Int, readline())
println("\nСоздание популяции...")
population = [init_conv() for _ in 1:pop_size]
println("Начало эволюционного обучения...")
println("Цель: достичь счета $target_score")
println("-"^60)
final_pop, training_stats, best_net, best_score = train_genetic!(
population, :conv,
target_score=target_score,
max_generations=max_generations,
mutation_rate=0.3
)
println("\nТестовый прогон лучшей сети...")
test_score = evaluate_network(best_net, :conv, test_episodes)
height, width = 15, 40
filters = 4
conv_params = 3 * 3 * 1 * filters + filters
fc_params = (height-2) * (width-2) * filters + 1
total_params = conv_params + fc_params
push!(results, NetworkResult(
name,
"Сверточная (Conv3x3×4 → FC)",
best_net,
:conv,
test_score,
training_stats,
total_params
))
println("\nОбучение завершено!")
println("Лучший счет в обучении: ", round(best_score, digits=2))
println("Тестовый счет: ", round(test_score, digits=2))
println("Нажмите Enter для продолжения...")
readline()
return results
end
function compare_results(results)
if isempty(results)
println("Нет результатов для сравнения!")
sleep(2)
return
end
print("\033[2J\033[H")
println("="^60)
println("СРАВНЕНИЕ ОБУЧЕННЫХ СЕТЕЙ")
println("="^60)
sorted_results = sort(results, by=r->r.test_score, rev=true)
println("\nРейтинг сетей (по тестовому счету):")
println("-"^60)
println("Место | Имя | Архитектура | Счет | Параметры")
println("-"^60)
for (i, r) in enumerate(sorted_results)
place = i == 1 ? "🥇" : i == 2 ? "🥈" : i == 3 ? "🥉" : " $i."
println("$place $(r.name) | $(r.architecture) | ", round(r.test_score, digits=2), " | $(r.params)")
end
if any(r -> !isempty(r.training_stats), sorted_results)
println("\nСтатистика обучения лучшей сети:")
best = sorted_results[1]
if !isempty(best.training_stats)
println("Количество поколений: $(length(best.training_stats))")
last_stat = best.training_stats[end]
first_stat = best.training_stats[1]
println("Начальный средний счет: ", round(first_stat[3], digits=2))
println("Финальный лучший счет: ", round(last_stat[2], digits=2))
println("Улучшение: ", round(last_stat[2] - first_stat[2], digits=2))
end
end
println("\nНажмите Enter для продолжения...")
readline()
end
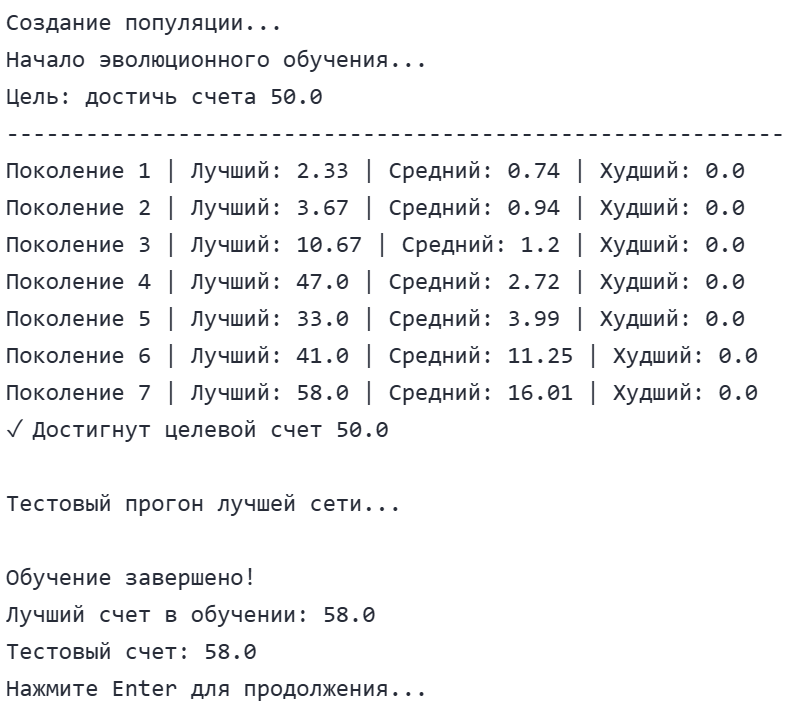
Для запуска проекта необходимо в командной строке вызвать main_menu(). Ниже представлены результаты запуска нашего проекта. Для частоты экспонента параметры для обоих сетей заданы идентичные.
.png)
.png)
Если вы самостоятельно запустите обучение обоих типов нейронных сетей, то заметите, что свёрточная сеть (CNN) обучается значительно медленнее, чем полносвязная. Это связано с принципиальным различием в архитектуре и объёме обрабатываемых данных: CNN работает с полной матрицей состояния игрового поля размером 15×40 (600 значений), выполняя на каждом шаге множество операций свертки для нескольких фильтров. В то же время полносвязная сеть получает на вход всего пять предобработанных признаков, что требует на порядки меньше вычислений. Такая разница в скорости обучения наглядно демонстрирует компромисс между сложностью модели и вычислительными затратами — более мощные архитектуры способны решать задачи лучше, но требуют значительно больше ресурсов для обучения.
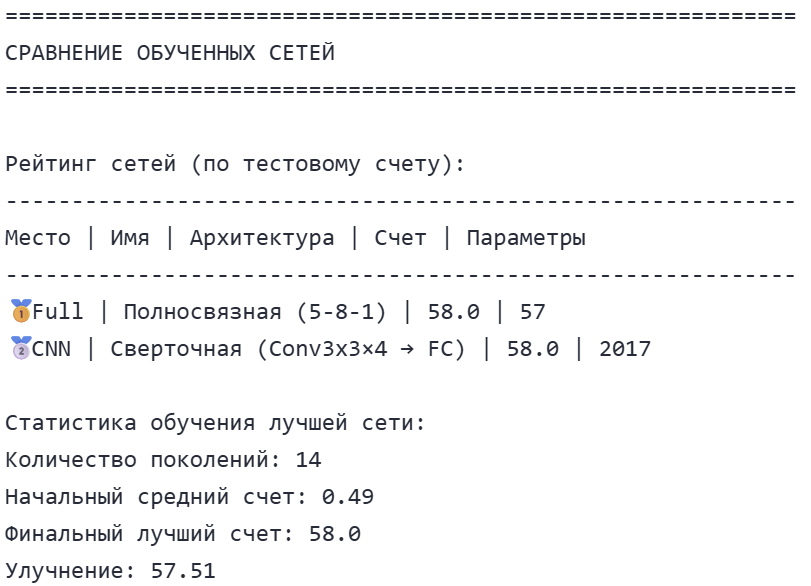
На основе представленных результатов можно сделать несколько важных выводов о работе эволюционного алгоритма и эффективности различных архитектур нейронных сетей в задаче игры Flappy Bird.
Обе нейронные сети — полносвязная (Fully Connected) и свёрточная (CNN) — достигли одинакового максимального счета в 58.0 очков.
Полносвязная сеть продемонстрировала исключительную эффективность: используя всего 57 параметров, она достигла того же результата, что и свёрточная сеть с 2017 параметрами (в 35 раз больше). Это иллюстрирует важный принцип машинного обучения: более сложная модель не всегда означает лучшую производительность, особенно когда задача может быть успешно решена простыми средствами.
Эволюционный алгоритм проявил высокую эффективность, достигнув максимального результата всего за 14 поколений. Начальный средний счет популяции составлял всего 0.49 очков, что свидетельствует о том, что случайно инициализированные сети практически не умели играть. За 14 поколений произошло улучшение на 57.51 очков — экспоненциальный рост производительности, демонстрирующий мощь эволюционных методов оптимизации.
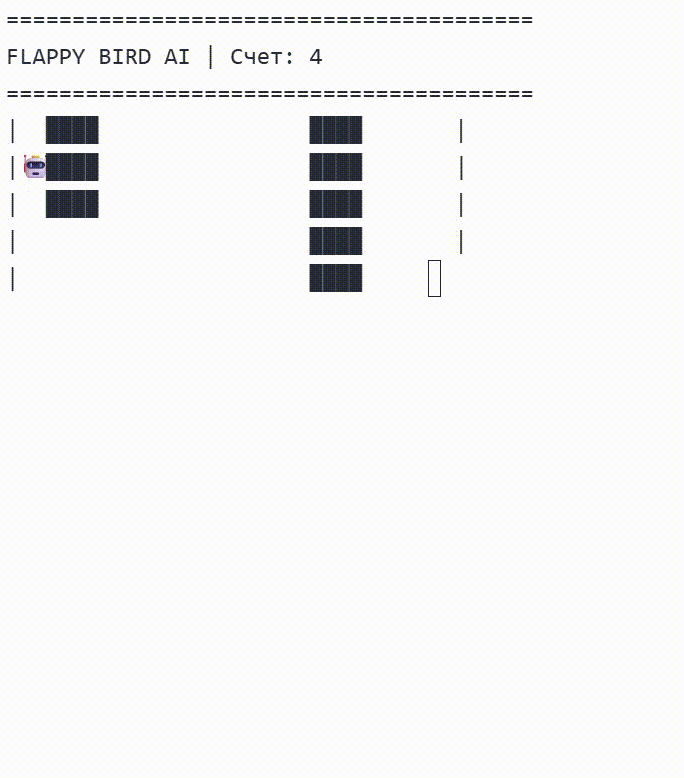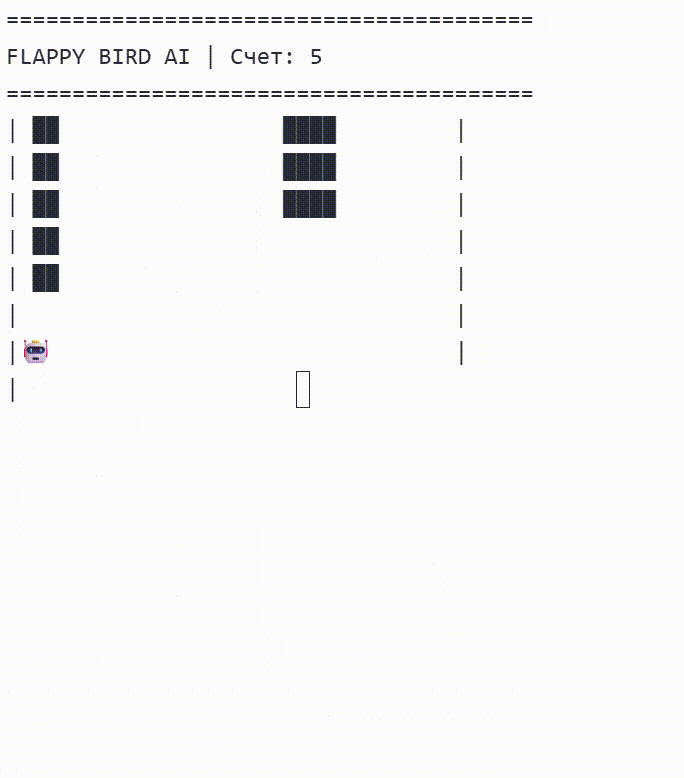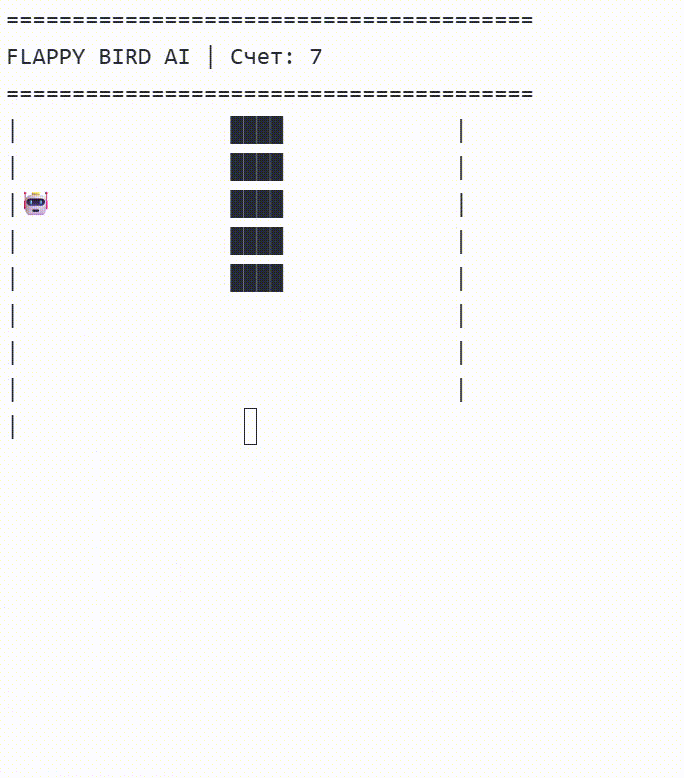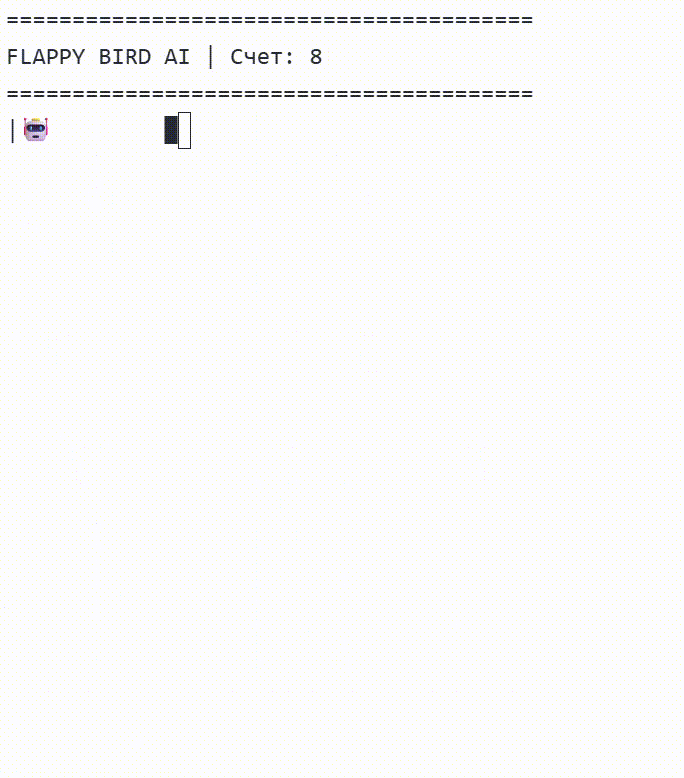
Ниже предоставлено, как в результате обе сети решили играть, обе сети поднимаются в верх поля и рассчитывают момент когда нужно перестать прыгать, чтоб попасть в отверстие.
Выводы
-
Простота против сложности: Для задач с четкими правилами и ограниченным пространством состояний простые архитектуры могут быть столь же эффективны, как и сложные, но требуют значительно меньше вычислительных ресурсов.
-
Эволюционные алгоритмы работают: Генетический подход без использования градиентов успешно оптимизировал обе архитектуры, показывая свою применимость для задач обучения с подкреплением.
-
Сходимость алгоритма: Быстрая сходимость (14 поколений) указывает на хорошо подобранные параметры эволюционного алгоритма — размер популяции, скорость мутации и стратегию отбора.
-
Потолок производительности: Одинаковый максимальный счет у обеих сетей может указывать либо на достижение максимально возможного результата в данной конфигурации игры, либо на ограничения самого игрового окружения.
Эти результаты подтверждают, что правильно реализованный эволюционный алгоритм может эффективно обучать нейронные сети даже сложным задачам, а выбор архитектуры должен соответствовать специфике решаемой проблемы, а не просто стремиться к максимальной сложности.