Сообщество Engee
Engee Community
/
Примеры и проекты
/
Идентификация объекта САУ с нечетким ПИД-регулятором

Идентификация объекта САУ с нечетким ПИД-регулятором

Автор
avatar-svetlanasvetlana
Notebook

Идентификация объекта системы управления с нечетким ПИД-регулятором

В этом примере решается сразу две задачи. Во-первых, мы идентифицируем объект управления на основе экспериментальных данных. Во-вторых, реализуем систему нечёткого вывода для ПИД-регулятора.

In [ ]: 
Pkg.add(["ControlSystemIdentification", "FuzzyLogic"])
using ControlSystemIdentification, FuzzyLogic

Напомню, что рабочий процесс идентификации выглядит следующим образом:

  1. Сбор данных эксперимента

  2. Выбор структуры модели

  3. Идентификация модели

  4. Валидация модели

Идентификация объекта управления

Сбор экспериментальных данных с объекта управления

Имитация экспериментальной установки объекта управления представлена в модели plant.engee. Объект управления - это дискретная система с одним входом и одним выходом. Также в модель добавлен шум и небольшое запаздывание.

Идентификация объекта будет производиться по переходному процессу, для этого на вход системы подадим ступеньку.

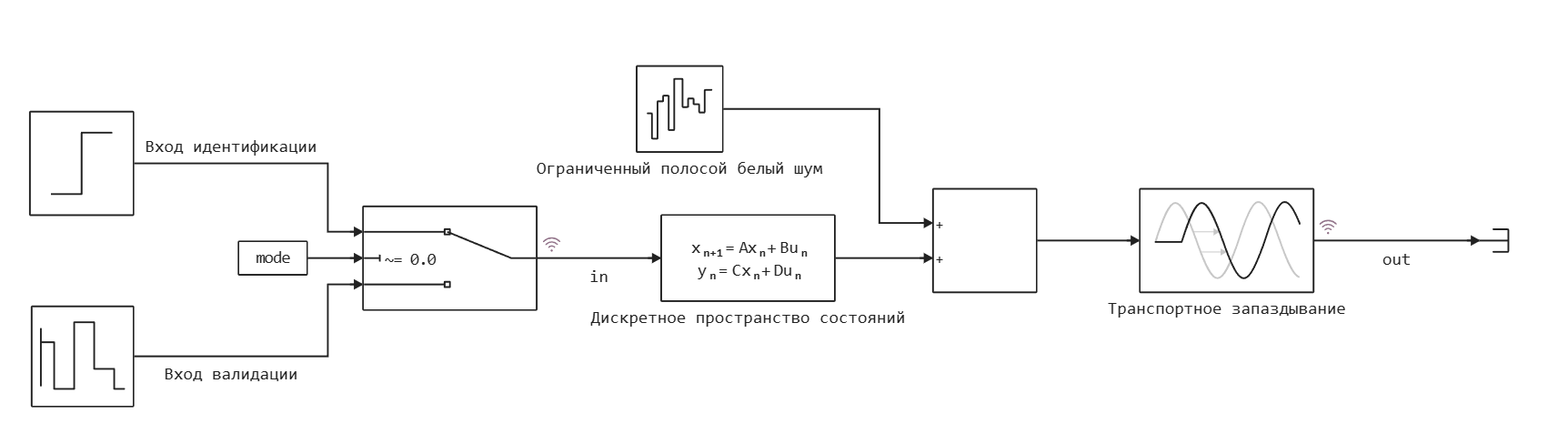
plant_1753359832841.png

Запишем данные для идентификации:

In [ ]: 
mode = 1; # Запись данных для идентификации
if "Plant" in [m.name for m in engee.get_all_models()]
    m = engee.open( "Plant" ) # загрузка модели
else
    m = engee.load( "Plant.engee" )
end
results = engee.run(m, verbose=true)

Building...
Progress 0%
Progress 100%
Progress 100%
Out[0]:
SimulationResult(
    "out" => WorkspaceArray{Float64}("Plant/out")
,
    "in" => WorkspaceArray{Float64}("Plant/in")

)
In [ ]: 
dataout = collect(results["out"]);
datain = collect(results["in"]);
# Частота дискретизации системы из вектора времени
Ts = dataout.time[2] - dataout.time[1]
ident_data = iddata(dataout.value, datain.value, Ts)
plot(ident_data)
Out[0]:

Запишем данные для валидации модели:

In [ ]: 
mode = 0; # Запись данных для валидации
if "Plant" in [m.name for m in engee.get_all_models()]
    m = engee.open( "Plant" ) # загрузка модели
else
    m = engee.load( "Plant.engee" )
end
results = engee.run(m, verbose=true)

Building...
Progress 0%
Progress 100%
Progress 100%
Out[0]:
SimulationResult(
    "out" => WorkspaceArray{Float64}("Plant/out")
,
    "in" => WorkspaceArray{Float64}("Plant/in")

)
In [ ]: 
dataout = collect(results["out"]);
datain = collect(results["in"]);
# Частота дискретизации системы из вектора времени
Ts = dataout.time[2] - dataout.time[1]
val_data = iddata(dataout.value, datain.value, Ts)
plot(val_data)
Out[0]:

Выбор структуры модели и идентификация

Будем идентифицировать линейную стационарную систему в пространстве состояний. Порядок системы выберем равным 3.

Для идентификации выберем метод ошибки прогнозирования PEM ( prediction-error method). Это простой, но эффективный алгоритм идентификации линейных стационарных систем с дискретным временем в форме пространства состояний. Метод также позволяет получить начальные состояния системы.

In [ ]: 
nx = 3; # порядок системы
sys, x0 = newpem(ident_data,nx)

Iter     Function value   Gradient norm 
     0     3.784040e-04     9.789230e-03
 * time: 0.19949603080749512
    50     2.082491e-04     4.272067e-04
 * time: 0.2358410358428955
   100     2.077983e-04     4.445332e-03
 * time: 0.3109588623046875
   150     2.068965e-04     6.060038e-03
 * time: 0.39757585525512695
   200     2.058789e-04     3.800742e-03
 * time: 0.4177060127258301
   250     2.057405e-04     2.125884e-03
 * time: 0.45604991912841797
   300     2.056074e-04     6.434034e-04
 * time: 0.48035192489624023
   350     2.055462e-04     3.334684e-04
 * time: 0.5061249732971191
   400     2.053596e-04     1.005185e-03
 * time: 0.5335268974304199
   450     2.051661e-04     9.945758e-03
 * time: 0.5657720565795898
   500     2.050343e-04     1.161464e-03
 * time: 0.6026959419250488
   550     2.048684e-04     1.551165e-02
 * time: 0.6348810195922852
   600     2.047113e-04     1.148014e-02
 * time: 0.6805129051208496
   650     2.046216e-04     2.184856e-02
 * time: 0.6981239318847656
   700     2.045511e-04     8.645446e-03
 * time: 0.7165648937225342
   750     2.044672e-04     1.919704e-02
 * time: 0.7359099388122559
   800     2.043937e-04     2.137336e-02
 * time: 0.7552690505981445
   850     2.042809e-04     1.807003e-02
 * time: 0.7735428810119629
   900     2.042222e-04     2.871188e-02
 * time: 0.7964169979095459
   950     2.041250e-04     1.880932e-02
 * time: 0.8146660327911377
  1000     2.040802e-04     1.426929e-01
 * time: 0.8476660251617432
  1050     2.039567e-04     7.880180e-02
 * time: 0.8641018867492676
  1100     2.039079e-04     1.105847e-01
 * time: 0.8808779716491699
  1150     2.038122e-04     3.309354e-01
 * time: 0.89768385887146
  1200     2.037250e-04     5.343228e-01
 * time: 0.9144978523254395
  1250     2.036590e-04     2.938638e-01
 * time: 0.9343979358673096
  1300     2.036076e-04     1.312110e+00
 * time: 0.9605119228363037
  1350     2.035490e-04     1.029981e+00
 * time: 0.9860918521881104
  1400     2.034784e-04     1.900128e+00
 * time: 1.0114190578460693
  1450     2.034470e-04     1.202898e+00
 * time: 1.0391180515289307
  1500     2.034154e-04     1.747894e-01
 * time: 1.0554909706115723
  1550     2.033921e-04     1.671672e+00
 * time: 1.0719490051269531
  1600     2.033679e-04     3.414074e+00
 * time: 1.0886778831481934
  1650     2.033440e-04     9.629020e+00
 * time: 1.1050329208374023
  1700     2.033089e-04     6.344263e+00
 * time: 1.1232068538665771
  1750     2.032809e-04     3.688618e+00
 * time: 1.1415619850158691
  1800     2.032635e-04     1.999306e+01
 * time: 1.1600329875946045
Out[0]:
(sys = PredictionStateSpace{ControlSystemsBase.Discrete{Float64}, ControlSystemsBase.StateSpace{ControlSystemsBase.Discrete{Float64}, Float64}, Matrix{Float64}, Matrix{Float64}, Matrix{Float64}, Matrix{Float64}}
A = 
 0.3140163495012443     3.7117022260861     0.0
 0.11023755964659158    1.6140225481406154  0.07598141692800656
 0.0                  -12.659066417167994   0.21882581128873133
B = 
 -3.320403895114945
  1.7883472038146635
 -7.720330696701567
C = 
 -6.177421822749285  -26.798969096921468  -3.5509173987959497
D = 
 0.0

Sample Time: 0.1 (seconds)
Discrete-time state-space model, x0 = [1.2762453764639579, -0.09723096657064308, -1.486442954748024], res =  * Status: success

 * Candidate solution
    Final objective value:     2.032499e-04

 * Found with
    Algorithm:     BFGS

 * Convergence measures
    |x - x'|               = 0.00e+00 ≤ 0.0e+00
    |x - x'|/|x'|          = 0.00e+00 ≤ 0.0e+00
    |f(x) - f(x')|         = 0.00e+00 ≤ 1.0e-16
    |f(x) - f(x')|/|f(x')| = 0.00e+00 ≤ 0.0e+00
    |g(x)|                 = 1.83e-02 ≰ 1.0e-12

 * Work counters
    Seconds run:   1  (vs limit 100)
    Iterations:    1841
    f(x) calls:    2387
    ∇f(x) calls:   1841
, nlp = Float64[])

Валидация модели

Проверим идентификацию на тех же данных, на которых проводилась идентификация

In [ ]: 
simplot(ident_data, sys)
Out[0]:

И проверим на специальном валидационном наборе данных

In [ ]: 
simplot(val_data, sys)
Out[0]:

Метод показал хороший результат идентификации.

Система управления с нечетким ПИД-регулятором

Вернемся к моделированию системы управления с нечетким контроллером. Мы получили модель объекта управления из экспериментальных данных.

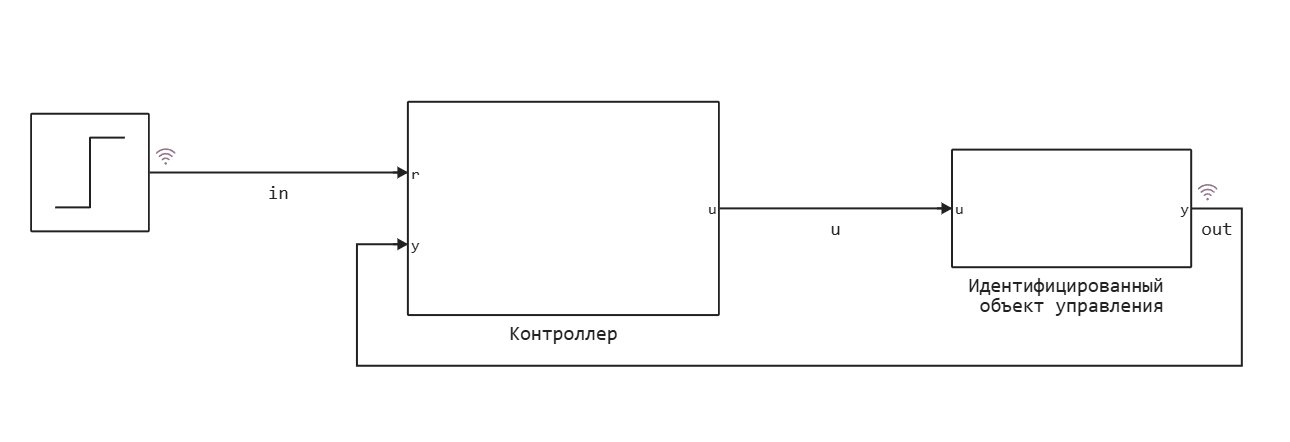
fuzzycontroller_1753369066574.png

Результат идентификации будет использоваться в блоке Дискретное пространство состояний (Discrete State Space) для моделирования объекта управления.

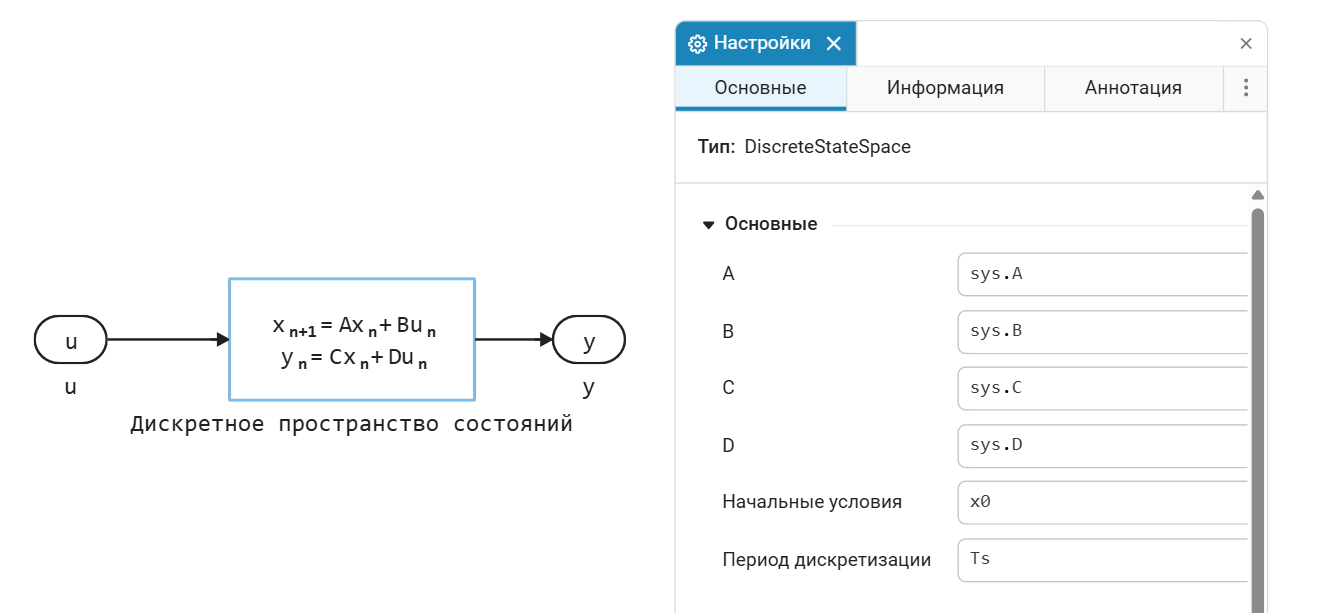
fuzzycontroller_1753369100219.png

Осталось добавить контроллер в контур системы управления. В этом примере используется следующая структура контроллера с нечёткой логикой:

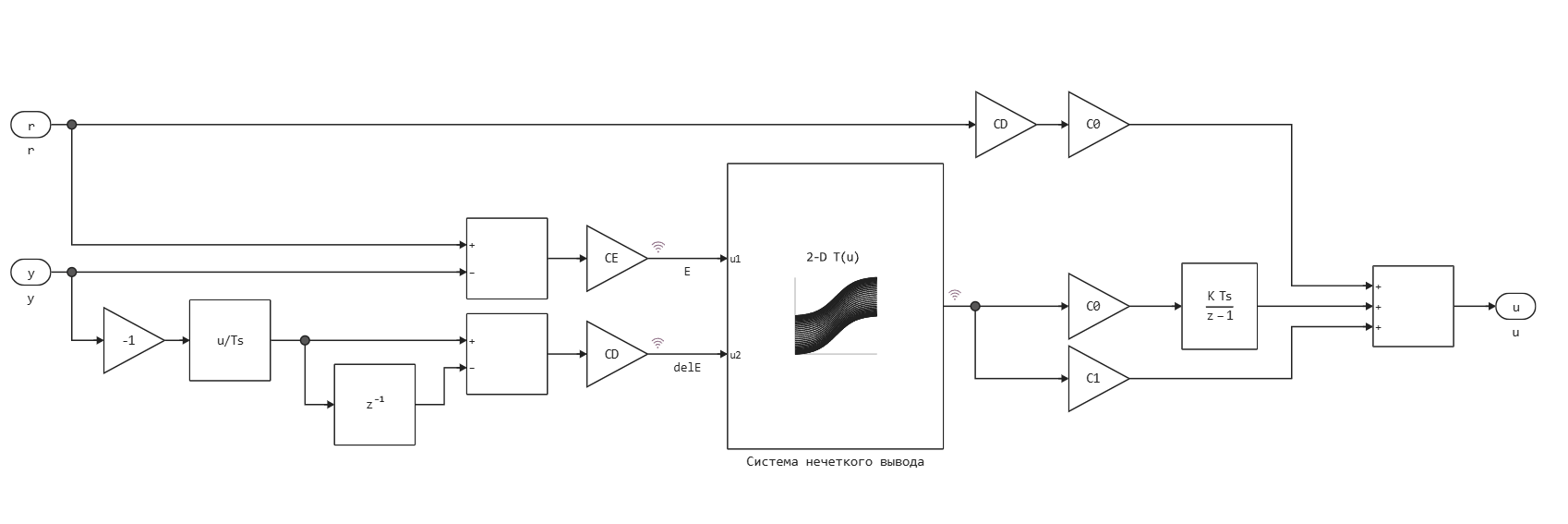
fuzzycontroller_1753362744936.png

На вход системы нечеткого вывода поступают нормализованные значения ошибки и производной ошибки . Входные значения нормализуются с помощью коэффициентов масштабирования и так, чтобы они находились в диапазоне [-1,1].

Система нечеткого вывода выдает результат в диапазоне [-1, 1], который масштабируется коэффициентами и .

In [ ]: 
CE = 10;
CD = 4.9829;
C0 = 2.5179;
C1 = 1.8103;

Система нечеткого вывода представлена в виде блока Табличной функции (Lookup table). Процесс формирования поверхности отклика для этой таблицы показан ниже:

In [ ]: 
fis = @sugfis function FCtrl(E, delE)::U
    E := begin
        domain = -10.0:10.0
        N = GaussianMF(-10.0, 7.0)
        P = GaussianMF(10.0, 7.0)
    end

    delE := begin
        domain = -10.0:10.0
        N = GaussianMF(-10.0, 7.0)
        P = GaussianMF(10.0, 7.0)
    end    

    U := begin
        domain = -20.0:20.0
        Min = -20.0
        Zero = 0.0
        Max  = 20.0
    end

   # Работающие правила
   E == N  && delE == N  -->  U == Min
   E == N  && delE == P  -->  U == Zero
   E == P  && delE == N  -->  U == Zero
   E == P  && delE == P  -->  U == Max

end;
In [ ]: 
plot(fis, :E, ylabel="Функция принадлежности", w = 2)
Out[0]:
In [ ]: 
plot(fis, :delE, ylabel="Функция принадлежности", w = 2)
Out[0]:

Сформируем поверхность отклика для того, чтобы поместить ее в блок Табличной функции (Lookup table).

In [ ]: 
errBrkpts = -10.0:0.5:10.0 
rateBrkpts = -10.0:0.5:10.0
LookUpTableData = zeros(length(errBrkpts), length(rateBrkpts))
i = 0;
for e in errBrkpts
    i = i+1
    j = 0;
    for de in rateBrkpts
        j = j+1
        LookUpTableData[i, j] = fis([e, de])[:U]
    end
end
surface(errBrkpts, rateBrkpts, LookUpTableData, xlabel="ΔE", ylabel="E", zlabel="U", title="Поверхность отклика", camera=(30, 30))
Out[0]:

Запустим модель системы управления и проверим работу регулятора.

In [ ]: 
if "Fuzzycontroller" in [m.name for m in engee.get_all_models()]
    m = engee.open( "Fuzzycontroller" ) # загрузка модели
else
    m = engee.load( "Fuzzycontroller.engee" )
end
fuzzyresults = engee.run(m, verbose=true)

Building...
Progress 0%
Progress 71%
Progress 100%
Progress 100%
Out[0]:
SimulationResult(
    "out" => WorkspaceArray{Float64}("Fuzzycontroller/out")
,
    "in" => WorkspaceArray{Float64}("Fuzzycontroller/in")

)
In [ ]: 
fuzzydataout = collect(fuzzyresults["out"]);
fuzzydatain = collect(fuzzyresults["in"]);

На графики мы видим реакцию системы управления на ступенчатое воздействие.

In [ ]: 
plot(fuzzydataout.time, fuzzydataout.value, titel = "Система управления с нечетким ПИД-регулятором", label="выход")
plot!(fuzzydatain.time, fuzzydatain.value, label="вход")
Out[0]:

Вывод

В результате мы получили работающую систему управления с нечетким ПИД-регулятором. Модель объекта управления не была заранее известна, а получена идентификацией на основе экспериментальных данных.

Группа видимости
ПубличноПросматривать контент могут все пользователи сообщества

Тип

Модель динамической системы

Краткое описание

Система управления с нечетким ПИД-регулятором. Объект управления идентифицирован на основе экспериментальных данных

Связанные материалы

Пусто

Теги

Категории

Отраслевые примененияУправление в технических системах

Языки

    Julia

Форматы

    engee
    ngscript

Уровень

    Продвинутый

Статус

Опубликовано

Обновлено

Источник

Сообщество