Имперский марш
Играем "Имперский марш" на КПМ РИТМ
В этом примере мы рассмотрим, как написать мелодию при помощи скрипта Engee и затем сыграть её на КПМ РИТМ.
Введение
В упрощённом представлении, любая мелодия - это последовательность звуков различной высоты и длительности, а также их отсутствия (пауз). Звуки можно описать гармоническими сигналами разной высоты. Высота звука в свою очередь определяется частотой следования такого сигнала. Резюмируя, задачу написания мелодии технически можно представить как задачу формирования последовательности частот единого сигнала с различной продолжительностью.
Подготовка мелодии
Исходная мелодия описывается нотами на изображении ниже.

Для удобства её перевода "в цифру" пройдём следующие шаги:
-
Каждой ноте определим соответствующую частоту.
-
Паузу определим нулевой частотой.
-
Зададим функции альтераций - диеза и бемоля, которые соответственно повышают и понижают частоту ноты на полтона.
-
Определим минимальный период следования сигналов.
-
Зададим функции длительностей нот.
-
Сгенерируем результирующий вектор мелодии - последовательность частот сигнала в соответствии с темпом.
Ноты
Вычисление частот для всего звукоряда по равномерно темперированному музыкальному строю определяется следующим образом:
где - частота камертона (Ля первой октавы, или A4 по научной нотации),
- число полутонов для исследуемого звука относительно камертона, для которого .
Запишем определение числа для нот из 5 октав. Используем для их обозначения научную нотацию.
(C2, C♯2, D2, D♯2, E2, F2, F♯2, G2, G♯2, A2, A♯2, B2) = collect(-33:-22); # Большая октава
(C3, C♯3, D3, D♯3, E3, F3, F♯3, G3, G♯3, A3, A♯3, B3) = collect(-21:-10); # Малая октава
(C4, C♯4, D4, D♯4, E4, F4, F♯4, G4, G♯4, A4, A♯4, B4) = collect(-9:2); # Первая октава
(C5, C♯5, D5, D♯5, E5, F5, F♯5, G5, G♯5, A5, A♯5, B5) = collect(3:14); # Вторая октава
(C6, C♯6, D6, D♯6, E6, F6, F♯6, G6, G♯6, A6, A♯6, B6) = collect(15:26); # Третья октава
Звук
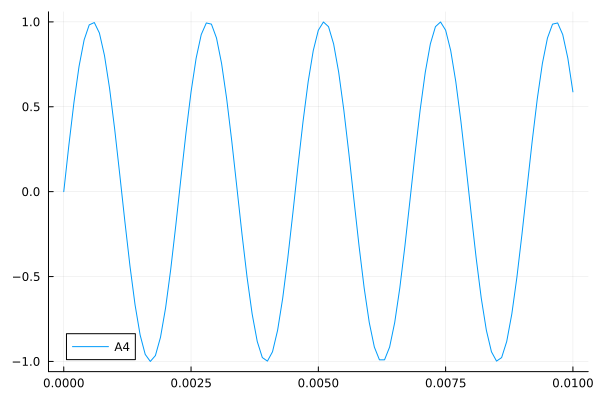
При таком определении частот звуков генерируемый гармонический сигнал в модели Engee будет выглядеть следующим образом:
t = collect(0:0.0001:0.01); f = 440*2^(A4/12);
gr()
plot(t, sin.(2*pi*f*t); label="A4")
Альтерации
Следующий этап подготовки - определение вспомогательных функций, которые упростят переписывание мелодии. Так можно определить диез (повышение частоты на полтона) и бемоль (повышение частоты на полтона) записанной ноты:
# Функции альтераций
♯(n) = n + 1; # Диез
♭(n) = n - 1; # Бемоль
Паузы
Если звук заданной тональности описывается определённой частотой, то пауза описывается нулевой частотой. Чтобы формировать паузы единой с нотами последовательностью чисел для определения частот, зададим паузу наименьшей длительности 𝄿 (шестнадцатая) числом , для которого результирующая частота . Паузы кратной длительности определяются через шестнадцатую.
𝄿 = [-999]; # Шестнадцатая пауза
𝄾 = vcat(𝄿, 𝄿); # Восьмая пауза
𝄽 = vcat(𝄾, 𝄾); # Четвертная пауза
𝄼 = vcat(𝄽, 𝄽); # Половинная пауза
Минимальный период
Минимальный период, с которым в модели Engee могут изменяться сигналы будет зависеть от минимальной длительности нот, пауз, а также от музыкального темпа.
Темп в исходной нотной записи задан 𝅘𝅥=100, то есть 100 четвертных длительностей в минуту.
Минимальная длительность в мелодии - шестнадцатая. Таким образом, минимальный период следования сигнала можно задать следующим образом:
tempo = 60/100/4 # Шестнадцатая длительность = 150 мс
Длительности
Для упрощения записи нот и их длительностей в коде определим функции для различных длительностей. Все длительности кроме шестнадцатой дополним шестнадцатой длительностью в конце. Это грубое допущение, но оно улучшит восприятие звукового сигнала в нашем прототипе музыкального проигрывателя на КПМ РИТМ.
# Функции нотных длительностей
𝅘𝅥𝅯(n) = [n]; # Шестнадцатая
𝅘𝅥𝅮(n) = [n, 𝄿...]; # Восьмая
𝅘𝅥𝅮⋅(n) = [n, n, 𝄿...]; # Восьмая с точкой
𝅘𝅥(n) = [n, n, n, 𝄿...]; # Четвертная
𝅗𝅥(n) = [n, n, n, n, n, n, 𝄾...]; # Половинная
Мелодия
Вся подготовка пройдена, в итоге исходную мелодию по нотам можно переписать так:
notes = vcat(𝅘𝅥(C4), 𝅘𝅥(C4), 𝅘𝅥(C4), 𝅘𝅥𝅮⋅(♭(A3)), 𝅘𝅥𝅯(♭(E4)),
𝅘𝅥(C4), 𝅘𝅥𝅮⋅(♭(A3)), 𝅘𝅥𝅯(♭(E4)), 𝅗𝅥(C4),
𝅘𝅥(G4), 𝅘𝅥(G4), 𝅘𝅥(G4), 𝅘𝅥𝅮⋅(♭(A4)), 𝅘𝅥𝅯(♭(E4)),
𝅘𝅥(♭(C4)), 𝅘𝅥𝅮⋅(♭(A3)), 𝅘𝅥𝅯(♭(E4)), 𝅗𝅥(C4),
𝅘𝅥(C5), 𝅘𝅥𝅮⋅(C4), 𝅘𝅥𝅯(C4), 𝅘𝅥(C5), 𝅘𝅥𝅮⋅(B4), 𝅘𝅥𝅯(♭(B4)),
𝅘𝅥𝅯(A4), 𝅘𝅥𝅯(♯(G4)), 𝅘𝅥𝅮(A4), 𝄾, 𝅘𝅥𝅮(♯(C4)), 𝅘𝅥(♯(F4)), 𝅘𝅥𝅮⋅(F4), 𝅘𝅥𝅯(E4),
𝅘𝅥𝅯(♭(E4)), 𝅘𝅥𝅯(D4), 𝅘𝅥𝅮(♭(E4)), 𝄾, 𝅘𝅥𝅮(♭(A3)), 𝅘𝅥(♭(C4)), 𝅘𝅥𝅮⋅(♭(A3)), 𝅘𝅥𝅯(♭(C4)),
𝅘𝅥(♭(E4)), 𝅘𝅥𝅮⋅(♭(C4)), 𝅘𝅥𝅯(♭(E4)), 𝅗𝅥(♯(G4)),
𝅘𝅥(C5), 𝅘𝅥𝅮⋅(C4), 𝅘𝅥𝅯(C4), 𝅘𝅥(C5), 𝅘𝅥𝅮⋅(B4), 𝅘𝅥𝅯(♭(B4)),
𝅘𝅥𝅯(A4), 𝅘𝅥𝅯(♯(G4)), 𝅘𝅥𝅮(A4), 𝄾, 𝅘𝅥𝅮(♯(C4)), 𝅘𝅥(♯(F4)), 𝅘𝅥𝅮⋅(F4), 𝅘𝅥𝅯(E4),
𝅘𝅥𝅯(♭(E4)), 𝅘𝅥𝅯(D4), 𝅘𝅥𝅮(♭(E4)), 𝄾, 𝅘𝅥𝅮(♭(A3)), 𝅘𝅥(♭(C4)), 𝅘𝅥𝅮⋅(♭(A3)), 𝅘𝅥𝅯(♭(E4)),
𝅘𝅥(C4), 𝅘𝅥𝅮⋅(♭(A3)), 𝅘𝅥𝅯(♭(E4)), 𝅗𝅥(C4),
𝄼, 𝄼);
В конце мелодии вставим паузу на целый такт (𝄼, 𝄼).
println("В нашей мелодии: ", sizeof(notes), " элементов шестнадцатой длительности.\n")
# @markdown ### Результаты переноса мелодии:
println("Вот как выглядит вектор с полутонами, из которого будут сгенерированы звуковые сигналы:\n")
print(notes)
Определение последовательности запускается автоматически при открытии модели примера. Для этого используются обратные вызовы модели.
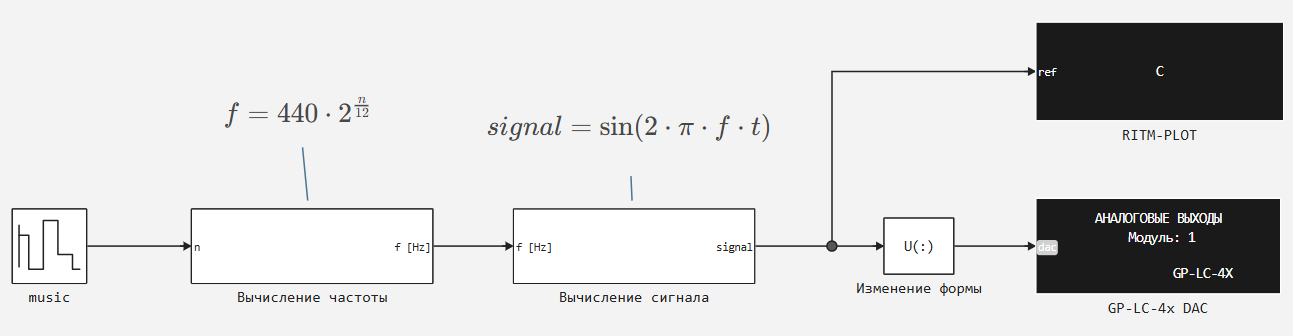
Модель примера
Полученную последовательность (мелодию) передадим в блок Repeating Sequence Stair - он с заданным периодом будет одно за другим передавать значения из вектора на выход. Эти значения далее при помощи блоков стандартной библиотеки Engee преобразуем в синусоидальный сигнал заданной частоты. Полученные сигналы будем передавать в блок аналогового выхода КПМ РИТМ, модуль RITMeX GP-LC-4X и в блок вывода графика на монитор.
Моделирование на КПМ РИТМ позволяет воспроизвести модель в режиме реального времени. Это нужно, например для точного контроля частоты и длительности генерируемого сигнала.
Настройки модели:
-
Размер шага моделирования, с -
1e-5 -
Режим симуляции -
Быстрый счёт -
Конец моделирования -
Inf -
Действие при переполнении шага расчёта -
Уведомить
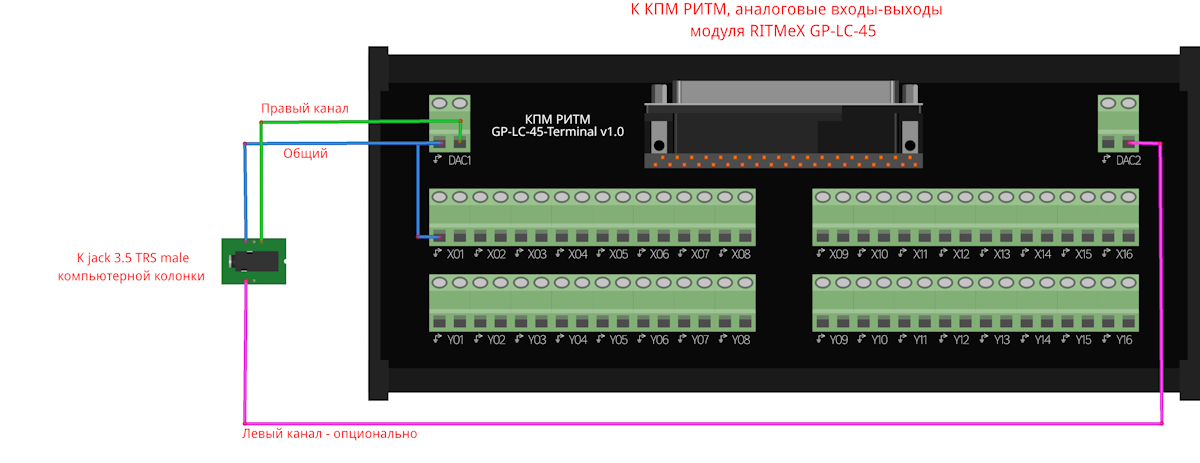
Аппаратная часть: вывод звука на динамик
Для вывода звука используем компьютерные колонки с аналоговым сигнальным входом jack TRS 3,5 мм. В примере используется один аудиоканал (монозвук). Для стереозвука на модуле GP-LC достаточно реализовать вывод сигнала со второго канала ЦАП DAC2. Подключение колонок к модулю РИТМ представлен на рисунке ниже:
Моделирование на РИТМе
Перед началом моделирования на машине реального времени необходимо установить подключение и несколько подготовительных шагов, которые описаны в соответствующем примере работы.
После запуска модели на РИТМе на мониторе можно наблюдать выдачу аналогового сигнала с различной длительностью и частотой, а в правом динамике будет слышна оцифрованная мелодия. Без подключения к РИТМу можно прослушать её в выводе кодовой ячейки ниже:
import Pkg; Pkg.add(["WAV","Base64"])
using WAV, Base64
using WAV, Base64
x, fs = wavread( "$(@__DIR__)/the imperial march.wav" );
buf = IOBuffer();
wavwrite(x, buf; Fs=fs);
data = base64encode(unsafe_string(pointer(buf.data), buf.size));
markup = """<audio controls="controls" {autoplay}>
<source src="data:audio/wav;base64,$data" type="audio/wav" />
Your browser does not support the audio element.
</audio>"""
display( "text/html", markup );
Запустить моделирование на РИТМе можно непосредственно из скрипта - для этого используем пакет поддержки внешнего оборудования и соответствующие методы программного управления.
Подробное описание процесса автоматизированного тестирования в реальном времени было дано в предыдущих примерах.
engee.package.install("Engee-Device-Manager");
# @markdown ## Подключение КПМ РИТМ
IP = "192.168.56.3" # @param {type:"string",placeholder:"192.168.56.3"}
порт = "8000" # @param {type:"string",placeholder:"8000"}
using Main.EngeeDeviceManager.Targets
using Main.EngeeDeviceManager.Targets.RITM_API
ritm = Targets.RITM.Ritm()
Targets.RITM_API.setUrl(ritm, "http://$IP:$порт/")
println("КПМ РИТМ подключен: ", RITM_API.isConnected(ritm))
# @markdown ## Запуск модели в режиме Standalone
имя_модели = "the_imperial_march" # @param {type:"string",placeholder:"hil_dcm"}
path = joinpath(@__DIR__, "$имя_модели.engee")
model = engee.load(path)
resp = Targets.upload_model(ritm, model)
println("\n", "Загрузка модели: ", resp)
resp = Targets.generate_executable_code(ritm, model, false)
println("\n", "Генерация кода: ", resp)
resp = Targets.compile_model(ritm, model)
println("\n", "Компиляция: ", resp)
Targets.start_model(ritm, model)
engee.close(model; force=true)
Заключение
В этом примере мы рассмотрели не только математические основы музыки и синтез сигналов по нотной записи, но и при помощи стенда реального времени воспроизвели простую мелодию. Это лишь небольшой пример из области цифрового синтеза звуковых сигналов, которые можно реализовать в Engee и на КПМ РИТМ.