Использование пакета Flux для анализа динамики цен акций Газпрома

#ЗАДАНИЕ ИСХОДНЫХ ДАННЫХ
import XLSX
using Plots, PlotThemes
using StatsBase

plotly()
theme(:dao)
xfGaz0 = XLSX.readdata("/user/Gazprom/AkzGASP00.xlsx", "Gazp", "A1:C2442")

n_gaz = length(xfGaz0[:, 1])
println("Число точек ВР = $(n_gaz-1)")

x = Float32.(xfGaz0[2:n_gaz, 1]);
y = Float32.(xfGaz0[2:n_gaz, 3]);

Iter = Int32[]
Strseed = String[]
Ertest = Float64[]
Ertrain = Float64[]


plot(x, y, title="Цена акции Газпром", legend=:topleft, wsize=(800, 500), label="Исходные данные", linewidth=2)
xlabel!("Номер даты с 01-01-2017 г. по 08-09-2023 г.")
ylabel!("руб")

Число точек ВР = 2441

# НОРМИРОВАНИЕ ДАННЫХ
xx = reshape(x, length(x), 1)
yy = reshape(y, length(y), 1)
xy = hcat(xx, yy)

dt = fit(ZScoreTransform, xy[:, 1:2], dims=1)
XY = StatsBase.transform(dt, xy[:, 1:2])
XY
plot(XY[:, 1], XY[:, 2], title="Нормированные исходные данные", linewidth=2, legend=false)

#=Формирование обучющей выборки, посроение нейронной сети и её обучение=#
using Flux
using Flux: train!
using Statistics
using Random


Random.seed!(456)
strseed="456"
NIer=500000 # число итерций обучения NC
nxyo_a = 1740    # начальный индекс обучающей выборки
nxyo_b = 2421 # конечный индекс ообучающей выборки
nxyt_a = 2422 # начальный индекс теста
nxyt_b = 2441 # конечный  индекс теста

x1 = XY[nxyo_a:nxyo_b, 1];
x2 = XY[nxyt_a:nxyt_b, 1];
y1 = XY[nxyo_a:nxyo_b, 2];
y2 = XY[nxyt_a:nxyt_b, 2];

x_train, x_test = (hcat(permutedims(x1)), hcat(permutedims(x2)))
y_train, y_test = (hcat(permutedims(y1)), hcat(permutedims(y2)))
data = [(x_train, y_train)]


model = Chain(Dense(1 => 23, tanh), Dense(23 => 1, bias=false))
loss(model, x, y) = mean(abs2.(model(x) .- y))
optim = Flux.setup(Adam(), model)

for epoch in 1:NIer
   Flux.train!(loss, model, data, optim)
end

ertrain=loss(model,model(x_train), y_train)
push!(Ertrain,ertrain)
push!(Strseed,strseed)

Xtr = reshape(x_train, length(x_train), 1)
Ytr = reshape(model(x_train), length(model(x_train)), 1)

plot(x1, y1,label="Исходные данные",legend=:bottomleft, linewidth=3)
plot!(Xtr, Ytr, seriestype=:scatter, label="Модель",ms=2)
xlabel!("нормализованный номер даты")
ylabel!("нормализованный y")
title!("Результаты обучения модели")

# обратное преобразование обучающей выборки и результатов обученной NS

XYcop =deepcopy(XY[nxyo_a:nxyo_b,1:2])
nXY = (nxyo_b-nxyo_a)+1
for i in 1:nXY
XYcop[i,2]=Ytr[i]
end
XYmod = StatsBase.reconstruct(dt, XYcop)
XYmod
XvYv = StatsBase.reconstruct(dt, XY[nxyo_a:nxyo_b,1:2])
XvYv

# Построение графика
#theme(:juno)
theme(:mute)
plot(XvYv[1:nXY, 1], XvYv[1:nXY, 2], label="Обучающие данные", legend=:topright, linewidth=2, linecolor=:blue)
plot!(XYmod[1:nXY, 1], XYmod[1:nXY, 2], seriestype=:scatter, label="Модель", ms=2,mc=:red,   wsize=(850, 500))
xlabel!("Номер даты")
ylabel!("Цена акций Газпрома руб.")
title!("Результаты обучения модели")
#savefig("GazModel.png")

#=Формирование тестовой последовательности и проверка модели на ней=#
# Обратное преобразование и построение графика

Xtest = reshape(x_test, length(x_test), 1)
Ymodtest = reshape(model(x_test), length(model(x_test)), 1)

XYtest = deepcopy(XY[nxyt_a:nxyt_b,1:2])
XYtest = StatsBase.reconstruct(dt, XYtest)
XYmodtest = hcat(Xtest,Ymodtest)
XYmodtest = StatsBase.reconstruct(dt, XYmodtest)

theme(:wong)

plot(XYtest[:, 1], XYtest[:, 2], label="Тестовые линии", legend=:topleft,linecolor=:blue, linewidth=2)
scatter!(XYtest[:, 1], XYtest[:, 2],label="Тестовые точки", ms=5, mc=:green)
plot!(XYmodtest[:, 1], XYmodtest[:, 2], seriestype=:scatter, label="Модель на тесте", ms=5,
mc=:red,wsize=(850, 500))
xlabel!("Номер даты")
ylabel!("Цена акций Газпрома руб")
title!("Результаты работы модели на тесте")

#Оценка точности прогноза на тесте при Random.seed!(456) и NIer=500000
println("Общее число точек ВР = $(n_gaz-1)")
println("Число точек обучающей последовательности = $(nxyo_b - nxyo_a +1)")
println("Число точек тестовой последовательности = $(nxyt_b - nxyt_a +1)")
Error_abs = mean(abs2.(XYmodtest[:, 2] .- XYtest[:, 2]))
Error_sqrt = sqrt(sum((XYmodtest[:, 2] .- XYtest[:, 2]) .^ 2)/(nxyt_b - nxyt_a+1))
println("Средняя абсолютная ошибка на тесте = $Error_abs")
println("Средняя квадратичная ошибка на тесте = $Error_sqrt")
println("Средняя абсолютная ошибка обучения = $ertrain")
push!(Iter, NIer)
push!(Ertest, Error_abs);

Общее число точек ВР = 2441
Число точек обучающей последовательности = 682
Число точек тестовой последовательности = 20
Средняя абсолютная ошибка на тесте = 4.6664014
Средняя квадратичная ошибка на тесте = 2.1601856
Средняя абсолютная ошибка обучения = 10.322577

using DataFrames
#Журнал испытаний модели
Gurnal = hcat(Strseed, Iter, Ertrain, Ertest)
Gurnaldf=DataFrame(Gurnal, :auto)
Gurnaldf = select(Gurnaldf, "x1" => "Seed", "x2" => "Niter", "x3" => "Ertrain ",
 "x4" => "Ertest")

# Определение остатков после обучения модели и их анализ
using Statistics
using HypothesisTests

Delta = XvYv[1:nXY, 2] - XYmod[1:nXY, 2];
@show M_ost = round(mean(Delta),sigdigits=2);
@show Sigma= sqrt(varm(Delta, M_ost));

theme(:mute)
plot(XvYv[1:nXY, 1], Delta, label="Остатки", legend=:topright, linewidth=1, linecolor=:red, 
wsize=(850, 500))
plot!(hline!([M_ost], label="Среднее", lw=3, lc=:red, linestyle=:dash))
xlabel!("Номер даты")
ylabel!("Остатки руб.")
title!("Остатки обученной  модели")

M_ost = round(mean(Delta), sigdigits = 2) = 0.22f0
Sigma = sqrt(varm(Delta, M_ost)) = 13.413914f0

# Проверка статистических гипотез о статистических свойствах остатков

using HypothesisTests
# Одновыборочный t-тест
xbar::Real = M_ost
stddev::Real=Sigma
n::Int=682
μ0::Real = 0
OneSampleTTest(xbar,stddev, n, μ0)

#=Краткое изложение теста:
результат с 95%-ной уверенностью: не удалось отвергнуть h0
двустороннее p-значение: 0,9736=#

One sample t-test
-----------------
Population details:
    parameter of interest:   Mean
    value under h_0:         0
    point estimate:          0.22
    95% confidence interval: (-0.7885, 1.229)

Test summary:
    outcome with 95% confidence: fail to reject h_0
    two-sided p-value:           0.6686

Details:
    number of observations:   682
    t-statistic:              0.42831112701694357
    degrees of freedom:       681
    empirical standard error: 0.5136453034506482

#Статистика Дурбина-Уотсона

Xx = reshape(XvYv[1:nXY, 1], 682, 1)
X::AbstractArray = Xx
e::AbstractVector = Delta
p_compute::Symbol =:approx
DurbinWatsonTest(X, e; p_compute)

#=Краткое изложение теста:
результат с 95%-ной достоверностью: отклонить h0
двустороннее p-значение: <1e-99
Статистика DW=0.263255 < 1.0 т.е.наличие положительной серийной корреляции=#

Durbin-Watson autocorrelation test
----------------------------------
Population details:
    parameter of interest:   sample autocorrelation parameter
    value under h_0:         "0"
    point estimate:          0.868419

Test summary:
    outcome with 95% confidence: reject h_0
    two-sided p-value:           <1e-99

Details:
    number of observations:     682
    DW statistic:               0.263163

Некоторые замечания и выводы по результам испытаний нейроной модели.

Анализ и прогнозирование временных рядов (ВР) одна из практически важных и достаточно теоретически узученых проблем. Умеются десятки математических моделей реализованных на разных языках прогроммирования, но общего решения вопроса прогнозирования сложного стохастического ВР в сфере точного знания не существует. Сейчас, когда такие модели как нейронные сети (NS), позволяют получать впечатляющие результаты в разных областях, их широко применябт при анализе и прогнозе ВР.В данном небольшом проекте я обратился к давно мною анализируемому ВР стоимости акций компании Газпром. Мне приходилось применять для анализа данного ряда модели нейронных сетей, реализованных в экосистеме R(nnfor) и Python (tensorflow keras LSTM),но несмотря на изящество и сложность моделей получить стабильно точные прогнозы не удавалось. Сейчас я попытался с использованием пакета Flux Julia посмотреть как он может работать при решении этой задачи на основе простой двухслойной сети прямой передачи (FFNN).
Но прежде чем проанализировать полученые мною результаты, изложу моё понимание факторов влияющих на точность прогнозов ВР GazProm с помощью нейросетевых моделей:

1.Газ один из важнейших источников энергии от которого зависит геополитическое, экономическое военное,и социальное положение как его производитей так и потребителей. Он производится и потребляется в исключительно конфликтых и сложных природных и социально-экомических условиях. Количество факторов влияющих на формирование и динамику его цены огромно и главное многие из них латентные, не имеющих внешних измерителей. Поэтому, построение сколько нибудь точной модели принципиально невозможно.Taк как ВР не полностью скрыты механизмыего его поведения,следовательно, нужно стремиться побороть сложность процесса приемлемой простотой его описания.

Таким образом, ВР стоимости акций АО Газпром как объект моделирования представляет собой сложную многоаспектную систему, которая генерирут посредством стахастических во многом скрытых механизмов непосредственно измеряемый ВР, в котором в случайные моменты времени формируются тенденции падения, стабилизации и роста,имеющие непредсказуемую длительность и постоянно сменяюшие друг друга.

2.Рассмотрим субъект моделирования и структуру его деятельности. Здесь имеется ввиду совокупный субъeкт (заказчик + аналитик) с акцентом на аналитическую составлющую.

Основные этапы и определение набора праметров модели и их идентификация:

Формулирование цели анализа и прогноза ВР.

Здесь исходя из практического измерения цели, небходимо определить требуемуемую точность прогноза, упреждающий период и временное расстояние между смежными точками прогноза. Под эти параметры формируется информационная база.То есть, выбирается из соотвествующих источников собственно первичный ВР (бирживые цены закрытия торгов и.т д), который исходя из целей ВР может агрегироваться во времени (неделя, месяц, квартал,год).На данном этапе принципиально важно определить минимально необходимый объем ВР (число точек первичного ряда) и требования к его качеству (наличие пропусков и целесобразность их аналитической ликвидации)

Выбор и обоснование аналитического инструментария прогнозирования

Априорные до модельные процедуры

Прежде всего, выбирается и анализируется набор классов моделей, способных выступить в качестве аналитической основы решения задачи прогнозирования ВР. Классы моделей анализируюся, как с точки зрения принципиальной возможности решать подобные задачи, так и с точки зрения разработанных и реализованных в виде программ и пакетов соотвествующих алгоритмов. Условно можно говорить о принципиальном и придельно общем выборе аналитического ядра создаваемой системы прогнозирования.Этот выбор похож на выбор типа двигателя для автомобиля (бензиновый, электрический, гибридный и.т.д). В нашем случае мы остановились на выборе класса нейросетевых моделей (гиперпараметр NN).Число классов нейромоделей досточно велико, укрупненно это: MLP(FNN),CNN,RNN(LSTM),трансформеры. Для работы с ВР лучше всего подходят FNN и LSTM. В нашем небольшом проекте мы остановились на FNN, хотя они обучаются гораздо хуже и медленнее LSTM. Но мы считаем, что время решения некритично, а меньшая степень обученности по фактическому ряду это скорее преимущество, так как сеть "схватывает"тенденции и не переучивается.Таким образом, мы выбираем гиперпараметр второго уровня (FNN). Описанная процедура осуществляется априори на домодельном уровне и может не осозноваться субъетом моделирования. Первые два уровня гиперпараметров идентифицируют классы математических моделей. В этом смысле они похожи на абстрактные типы в Julia.В дальнейшем мы будем рассматривать экземпляры выделенных классов моделей и конкретные данные как экземпляр класса ВР.

Процесс получения,оценки и структурированния исходных данных

Сначало определимся с данными. Для опробации мы взяли ВР цен акций Газпрома с 0101.2017 по 08.09.2023 (2441 точка). Для обучения данные с номерами с Ntain1=1740 по Ntrain2=2421 всего 682 точки. Так как исходный ряд был подготовлен и не содержит пропусков, то для имитации прогнозного периода берем 20 последних точек с Ntest1 =2422 по Ntest2 =2441. Это в рабочих днях составляет месяц (вполне разумный период, но его можно увеличивать и уменьшать). Следовательно, на данных мы определили следующие гиперпараметры: Ntain1,Ntrain2,Ntest1,Ntest2.Для того чтобы FNN нормально работала с данными необходимо их нормировать, а после получения результатов совершить обратное преобразование.

Выбор гиперпараметров FNN.

В качестве гиперпараметров для FNN необходимо рассматривать:

Nlayer - число слоев сети;
Nneuron - число нейронов в каждом слое;
Factiv - вид функции активации;
bias - смещение;
Aopt - алгоритм оптимизации;
loss - критерий оптимизации.

Мы поставили себе задачу показать, что простая FNN может при определенных условиях обеспечить приемлемую точность описания ВР цен акций Газпрома. Нами были выбранны следующие значения гиперпараметров:Nlayer=2;Nneuron =(23,1);Factiv = {tanh};bias=false; Aopt={Adam};loss = {MAE}.При заданных значениях этих гиперпараметров результаты работы нейросети определяются еще двумя параметрами NIer - число итерций обучения NC и Random.seed!(i) - начальное значение гегератора случайных чисел.

3.Разработка скрипта, его реализация и анализ полученных результатов.

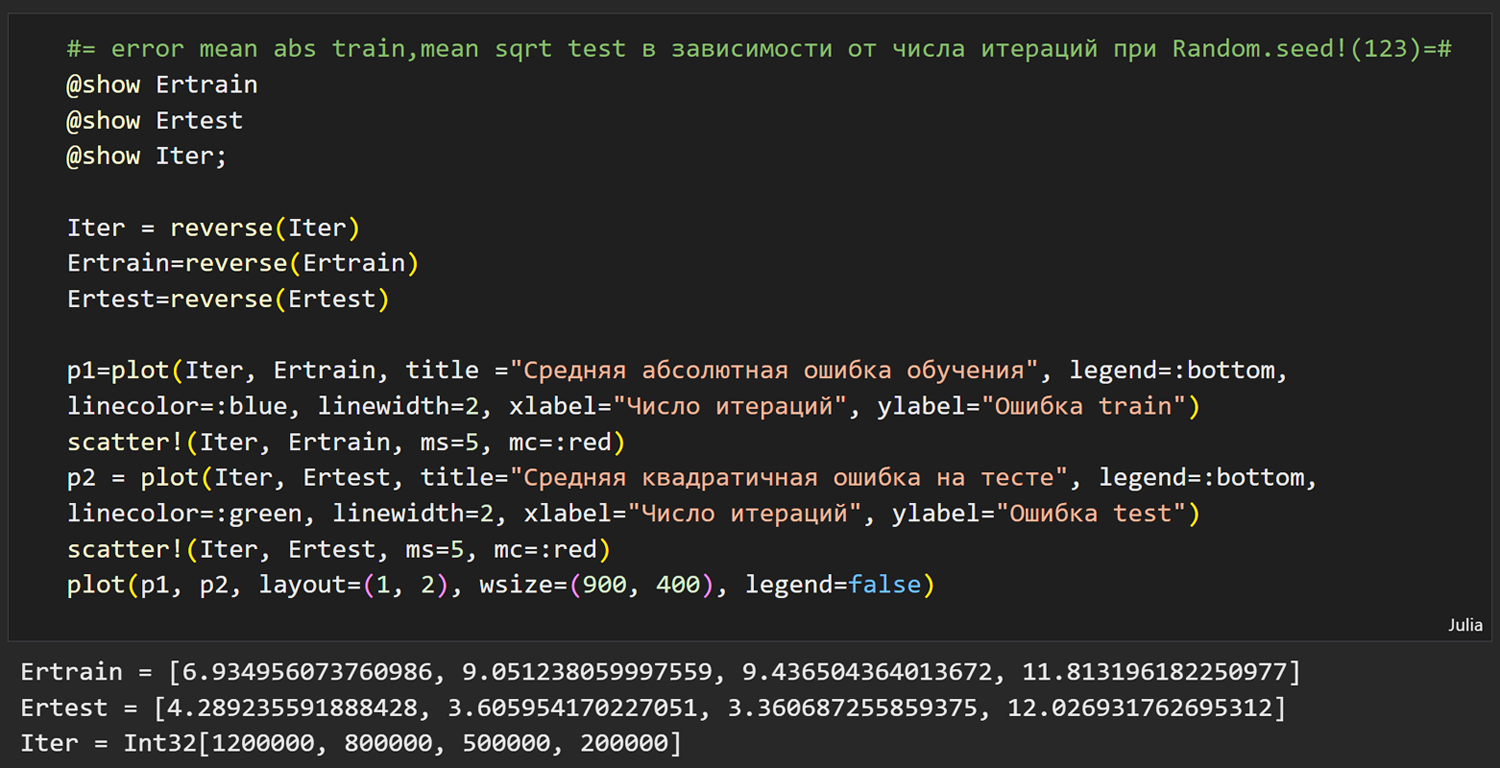
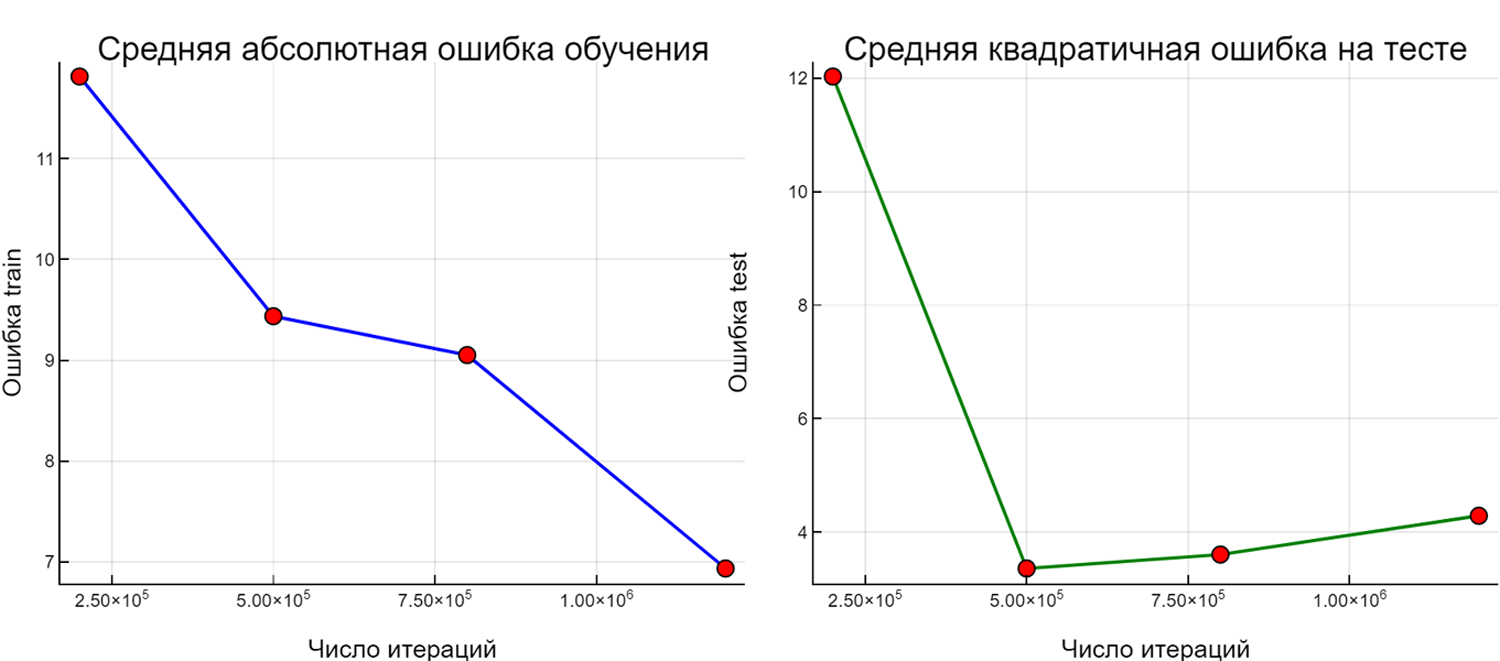
Мы разработали скрипт Julia c использованием пакета Flux (скрипт и результаты его работы приведены выше). В нем встроены простейшие инструменты фиксации результов моделирования и соотвествующих значений NIer и Random.seed!(i) (формируется журнал испытаний ).На первом этапе исследовалась зависимость точности обучения и точности на тесте от NIer при фиксированном и традиционном значениии Random.seed!(123). NIer варьировалось от 200000 до 1200000. Как видно на графике средняя абсолютная ошибка обучения падает от 11.81 (NIer=200000) до 6.93 (NIer=1200000).
Средне квадратичная ощибка на тесте имеет минимум 3.36 при NIer=500000. Начиная с этой величины NIer, повышение уровня обученности снижает точность на тесте. Затраты времени вполне приемлемые от 1мин.20с. до 4мин.30с. на Intel(R) Core(TM) i5-9400F CPU @ 2.90GHz 2.90 GHz и ОЗУ=16Гб.
Затем при NIer=500000 мы варьировали Random.seed, полученые результаты можно посмотреть в журнале испытаний.Ошибка на тесте изменяется очень сильно, в десятки раз.Наилучший результат получен при
Random.seed!(456): MAE = 4.45, MSE=2.11 . Это очень хорошие результаты.

4.Перспективы совершенствования системы.

Учитывая огромное влияния гиперпараметров на результаты моделирования необходимо включать в процесс моделирования существующие алгоритмы идентификации гиперпараметров, что потребует значительных вычислительных мощностей и, видимо, перехода на GPU.

Использование пакета Flux для анализа динамики цен акций Газпрома

Некоторые замечания и выводы по результам испытаний нейроной модели.

Тип

Краткое описание

Связанные материалы

Теги

Категории

Языки

Форматы

Уровень

Статус

Опубликовано

Обновлено

Источник

Row	Seed	Niter	Ertrain	Ertest
	Any	Any	Any	Any
1	123	500000	8.40837	10.9584
2	456	500000	10.3226	4.6664
3	456	500000	10.3226	4.6664
4	789	500000	4.02577	151.24
5	284	500000	69.4082	20.1988
6	456	500000	10.3226	4.6664