Исследование крутильных колебаний многомассовой системы
Исследование крутильных колебаний многомассовой системы
В данном примере будет показано моделирование и анализ крутильных колебаний многомассовой механической системы. Модель демонстрирует, как импульсное воздействие возбуждает собственные моды системы, и как резонансное воздействие приводит к значительному усилению колебаний.
Крутильные колебания возникают в системах с несколькими инерционными массами, соединенными упругими валами. Каждая такая система имеет набор собственных частот (мод), на которых происходит резонансное усиление колебаний.
Начальное возбуждение: импульсный момент 1000 Н⋅м длительностью 0.01 с.
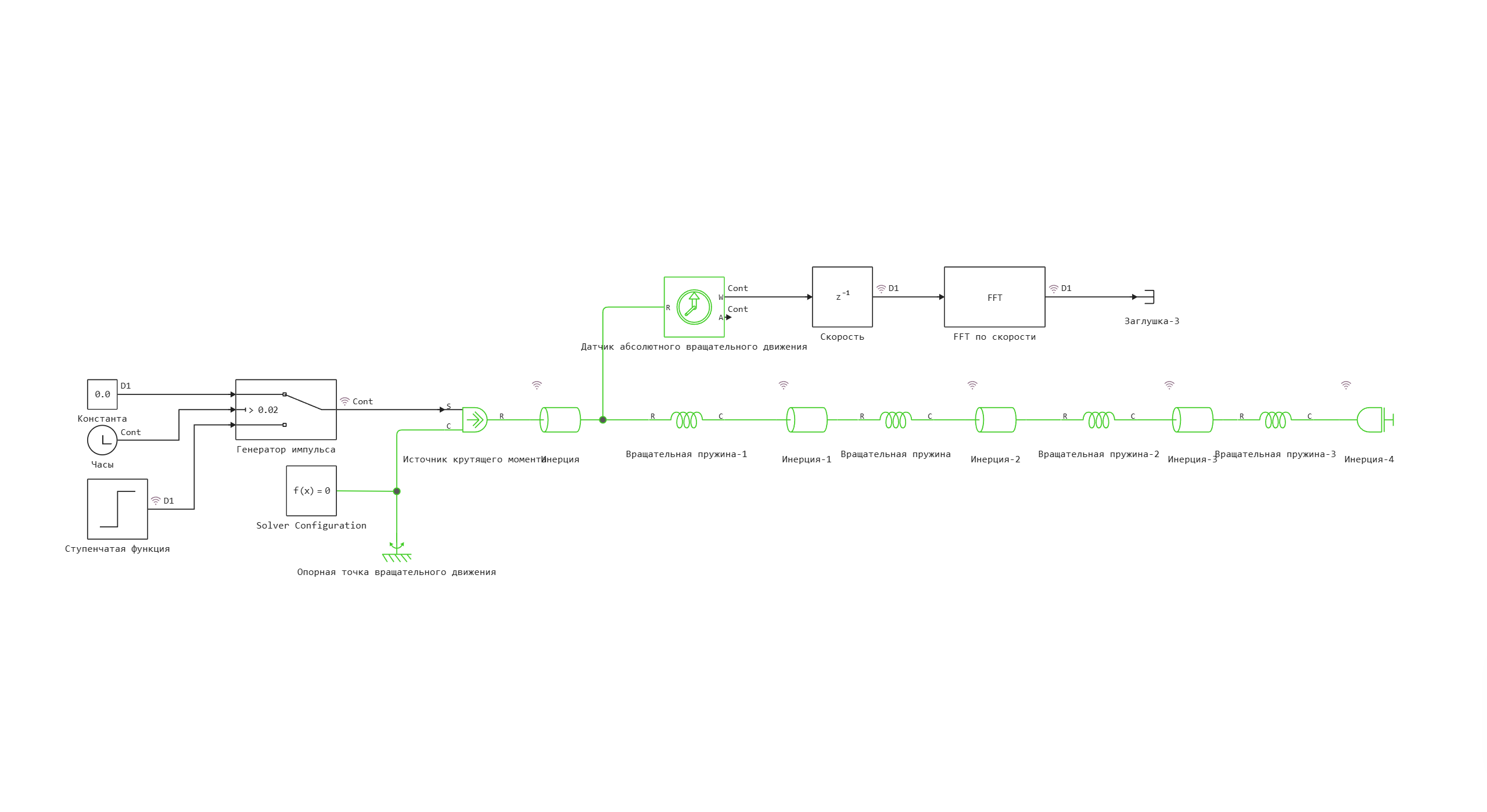
Схема модели:
Для реализации модели крутильных колебаний используется многомассовая система с упругими связями.
Определение функции для загрузки и запуска модели:
m = "torsional_oscillations"
function start_model_engee(m)
try
engee.close(m, force=true) # закрытие модели если открыта
catch err # в случае, если нет модели, которую нужно закрыть
# модель не была открыта
end
try
m = engee.load("$((@__DIR__))/$m.engee") # загрузка модели
engee.run(m) # запуск модели
catch err # в случае, если модель не загружена
m = engee.load("$((@__DIR__))/$m.engee") # загрузка модели
engee.run(m) # запуск модели
end
end
Определение функций для анализа:
Функция FFT анализа собственных частот:
using FFTW, DSP
function analyze_natural_frequencies(time_data, speed_data)
# Подготовка данных для FFT
dt = time_data[2] - time_data[1]
fs = 1/dt # Частота дискретизации
# Применение оконной функции для лучшего разрешения
windowed_data = speed_data .* hanning(length(speed_data))
# Вычисление FFT
fft_result = fft(windowed_data)
# Частотная ось
frequencies = fftfreq(length(fft_result), fs)
# Амплитудный спектр в dB
magnitude_db = 20 * log10.(abs.(fft_result) .+ 1e-10)
return frequencies, magnitude_db
end
Функция поиска пиков собственных частот:
using Peaks
function find_natural_frequencies(frequencies, magnitude_db, min_height=20)
# Поиск пиков в положительной части спектра
pos_freq_idx = frequencies .> 0
pos_freqs = frequencies[pos_freq_idx]
pos_magnitudes = magnitude_db[pos_freq_idx]
# Поиск локальных максимумов
peaks, _ = findmaxima(pos_magnitudes)
# Фильтрация по высоте
high_peaks = peaks[pos_magnitudes[peaks] .> min_height]
natural_freqs = pos_freqs[high_peaks]
amplitudes = pos_magnitudes[high_peaks]
return natural_freqs, amplitudes
end
Запуск симуляции с импульсным воздействием
start_model_engee(m);
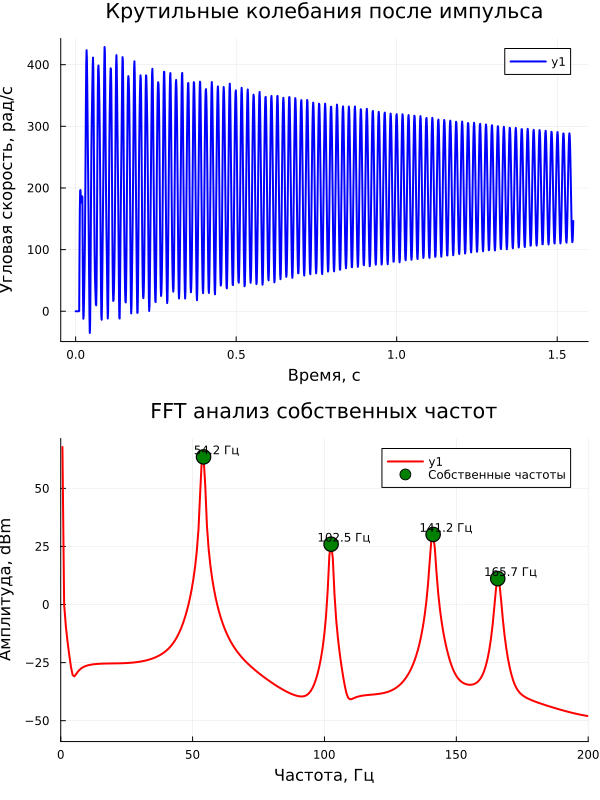
Запустив модель в среде моделирования, в окне "Визуализация сигналов" можно увидеть график сигнала скорости после БПФ (быстрого преобразования Фурье) в частотной области:
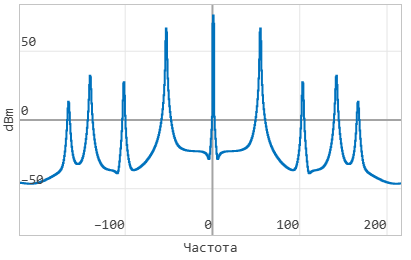
Проанализировав этот график можно обнаружить собственные частоты системы.
Построим аналогичный график в данном интерактивном скрипте, для этого необходимо вывести данные симуляции в переменные.
Вывод данных для анализа:
# Получение угловых скоростей всех инерций
omega1 = collect(simout["torsional_oscillations/FFT по скорости.1"]);
# Выделение времени и данных для анализа
time_data = omega1[:,1];
speed_data = omega1[:,2]; # Анализируем первую инерцию
Выполнение FFT анализа:
# FFT анализ для определения собственных частот
frequencies, magnitude_db = analyze_natural_frequencies(time_data, speed_data);
natural_freqs, amplitudes = find_natural_frequencies(frequencies, magnitude_db);
# Вывод найденных собственных частот
println("Обнаруженные собственные частоты:")
for (i, (freq, amp)) in enumerate(zip(natural_freqs, amplitudes))
println("$(i)-я мода: $(round(freq, digits=2)) Гц ($(round(amp .-30, digits=2)) dBm)")
end
Визуализация проведённого анализа:
using Plots
using Printf
function create_torsional_analysis_plots(time_data, speed_data, frequencies, magnitude_db)
gr()
# Преобразуем все данные в вещественные числа
real_frequencies = real.(frequencies)
real_magnitude_db = real.(magnitude_db)
real_time_data = real.(time_data)
real_speed_data = real.(speed_data)
# График временного отклика
p1 = plot(real_time_data, real_speed_data,
title="Крутильные колебания после импульса",
xlabel="Время, с",
ylabel="Угловая скорость, рад/с",
linewidth=2,
linecolor=:blue)
# График FFT спектра
pos_idx = (real_frequencies .> 0) .& (real_frequencies .< 300)
p2 = plot(real_frequencies[pos_idx], real_magnitude_db[pos_idx] .- 30,
title="FFT анализ собственных частот",
xlabel="Частота, Гц",
ylabel="Амплитуда, dBm",
xlim=(0, 200),
linewidth=2,
linecolor=:red)
# Выделение найденных собственных частот
experimental_freqs = natural_freqs
experimental_amps = amplitudes .- 30
scatter!(p2, experimental_freqs, experimental_amps,
markersize=8,
markercolor=:green,
markerstroke=:black,
label="Собственные частоты")
# Подписи частот
for (i, (freq, amp)) in enumerate(zip(experimental_freqs, experimental_amps))
annotate!(p2, freq+5, amp+3, text(@sprintf("%.1f Гц", freq), 8, :black))
end
# Объединение графиков
combined_plot = plot(p1, p2, layout=(2,1), size=(600,800))
return combined_plot
end
# Создание графиков
analysis_plots = create_torsional_analysis_plots(time_data, speed_data, frequencies, magnitude_db)
Явление резонанса на собственной частоте
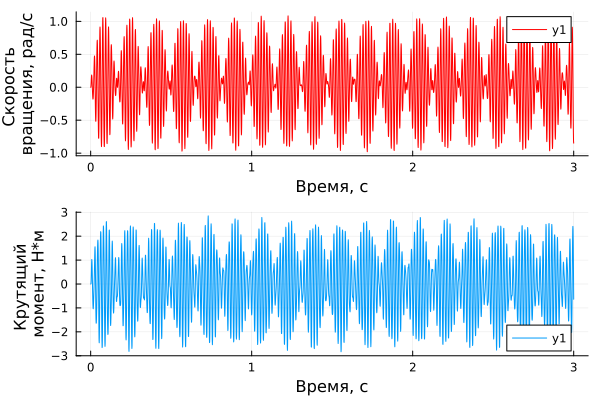
Теперь проверим, как разные частоты воздействующего источника крутящего момента влияют на угловую скорость первого блока инерции.
Амплитуда крутящего момента 1 Н*м.
Для этого запустим модель, где в качестве источника воздействия используется не генератор импульса, а синусоидальный сигнал.
Схема модели:
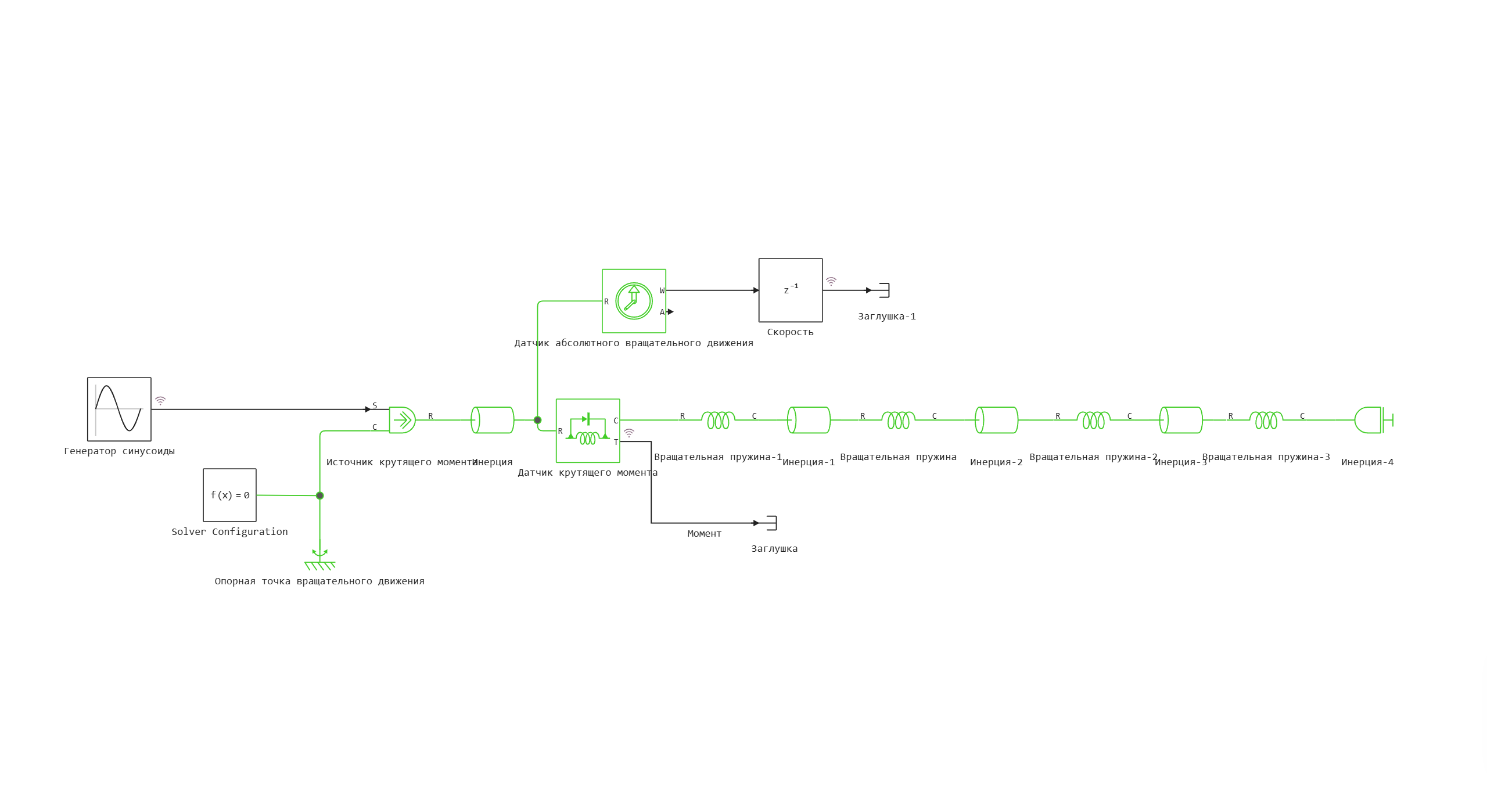
С помощью переменной omega определяем частоту синусоидального сигнала перед каждым запуском симуляции.
n = "torsional_oscillations_sin"
omega = 10
start_model_engee(n)
w = collect(simout["$n/Скорость.1"]);
torque = collect(simout["$n/Момент"]);
time_data1 = w[:,1];
speed_data1 = w[:,2];
time_torque = torque[:,1]
torque_data = torque[:,2]
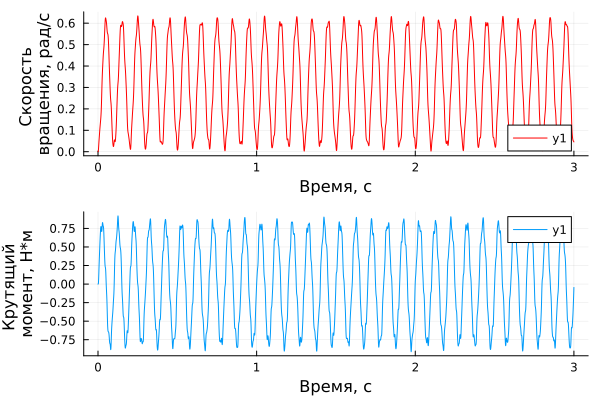
p1 = plot(time_data1, speed_data1, xlabel="Время, с", ylabel="Скорость \nвращения, рад/с", color="red")
p2 = plot(time_torque, torque_data, xlabel="Время, с", ylabel="Крутящий \nмомент, Н*м")
plot(p1,p2, layout=(2,1))
omega = 20
start_model_engee(n)
w = collect(simout["$n/Скорость.1"]);
torque = collect(simout["$n/Момент"]);
time_data1 = w[:,1];
speed_data1 = w[:,2];
time_torque = torque[:,1]
torque_data = torque[:,2]
p1 = plot(time_data1, speed_data1, xlabel="Время, с", ylabel="Скорость \nвращения, рад/с", color="red")
p2 = plot(time_torque, torque_data, xlabel="Время, с", ylabel="Крутящий \nмомент, Н*м")
plot(p1,p2, layout=(2,1))
omega = 30
start_model_engee(n)
w = collect(simout["$n/Скорость.1"]);
torque = collect(simout["$n/Момент"]);
time_data1 = w[:,1];
speed_data1 = w[:,2];
time_torque = torque[:,1]
torque_data = torque[:,2]
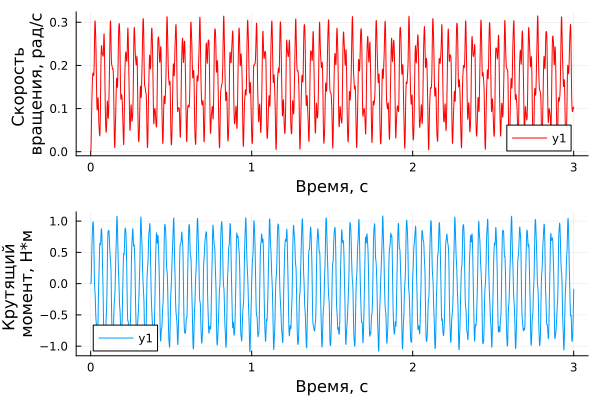
p1 = plot(time_data1, speed_data1, xlabel="Время, с", ylabel="Скорость \nвращения, рад/с", color="red")
p2 = plot(time_torque, torque_data, xlabel="Время, с", ylabel="Крутящий \nмомент, Н*м")
plot(p1,p2, layout=(2,1))
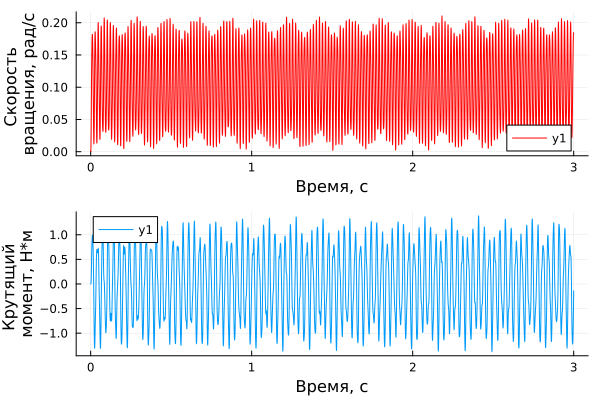
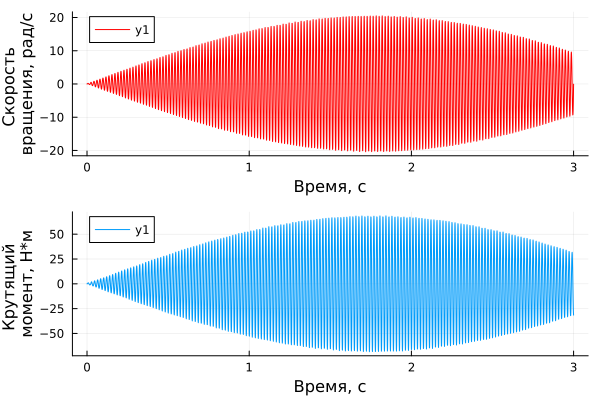
omega = natural_freqs[1] #Первая собственная частота
start_model_engee(n)
w = collect(simout["$n/Скорость.1"]);
torque = collect(simout["$n/Момент"]);
time_data1 = w[:,1];
speed_data1 = w[:,2];
time_torque = torque[:,1]
torque_data = torque[:,2]
p1 = plot(time_data1, speed_data1, xlabel="Время, с", ylabel="Скорость \nвращения, рад/с", color="red")
p2 = plot(time_torque, torque_data, xlabel="Время, с", ylabel="Крутящий \nмомент, Н*м")
plot(p1,p2, layout=(2,1))
omega = 60
start_model_engee(n)
w = collect(simout["$n/Скорость.1"]);
torque = collect(simout["$n/Момент"]);
time_data1 = w[:,1];
speed_data1 = w[:,2];
time_torque = torque[:,1]
torque_data = torque[:,2]
p1 = plot(time_data1, speed_data1, xlabel="Время, с", ylabel="Скорость \nвращения, рад/с", color="red")
p2 = plot(time_torque, torque_data, xlabel="Время, с", ylabel="Крутящий \nмомент, Н*м")
plot(p1,p2, layout=(2,1))
Видно, что в отличие от других частот, воздействие на собственной частоте вызывает многократное увеличение крутящего момента и частоты вращения инерции. Наблюдается явление "биения", которое, зачастую, сопровождается резонансом.
Выводы:
В данном примере была продемонстрирована комплексная модель анализа крутильных колебаний многомассовой системы.
Модель может быть адаптирована для различных крутильных систем: турбо-генераторных установок, приводов прокатных станов, судовых валопроводов и других промышленных механизмов.