Как посчитать знаменатель геометрической прогрессии?

Контекст

В этом примере я писал, что устройства релейной защиты часто определяют действующее значение тока и напряжения как результат фильтрации входного сигнала двумя ортогональными фильтрами (фильтр Фурье).

Также было показано, что свободные составляющие в сигналах энергосистемы (в первую очередь апериодические экспоненциальные составляющие) искажают результаты оценки действующего значения первой гармоники тока и напряжения.

Иными словами, если сигнал на входе устройства задан как:

то по дискретным отсчетам оценка происходит с методической погрешностью из-за наличия ненулевого и не равного бесконечности.

Для точных замеров (оценок), с которыми напрямую связано такое важное для релейной защиты понятие как селективность, необходимо это мешающее влияние убирать. В примере был показан один из вариантов, когда коэффициенты синусного и косинусного фильтров смещаются на определенную константу, что приводит к полной независимости оценок первой гармоники от апериодической составляющей в сигнале.

Начальная формулировка задачи

Для того, чтобы удалить из сигнала апериодическую составляющую необходимо знать параметр затухания . Здесь полная аналогия с удалением из сигнала мешающей частоты. Чтобы настроить подавляющий фильтр на какую-то конкретную частоту, желательно знать на какую именно. Так и для экспоненты, алгоритм подавления должен знать какой параметр затухания у подавляемой составляющей.

Итого мы приходим к задаче оценки параметра затухания экспоненты по ее дискретным отсчетам.

Еще точнее: если экспонента записана как

где - период дискретизации, с;
- номер отсчета, то достаточно оценить величину .

Конечная формулировка задачи

Даны отсчеты геометрической прогрессии

Каждый отсчет искажен шумом с нулевым средним и дисперсией . Найти (оценить) знаменатель наилучшим образом.
Под наилучшим образом будем понимать наименьшее смещение относительно верного знаменателя прогрессии и наименьшую дисперсию.

Для простоты будем работать с массивом (вектором) из 5 дискретных отсчетов:

Формулировка выглядит довольно простой, чтобы думать, что эта задача уже не решена 100 раз. Просто поисследуем разные варианты формул оценки, которые приходят в голову.

Что дано и что нужно найти еще раз показано на рисунке

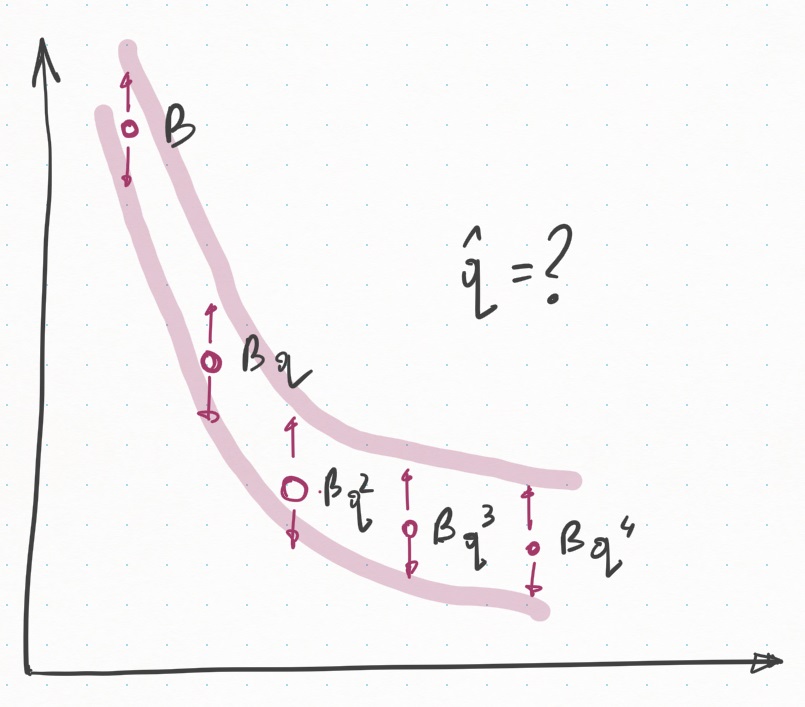
Варианты решения

"Нулевое" что приходит в голову

Простейшие оценки дают отношения соседних отсчетов:

Очевидно, что шум довольно сильно влияет на них, поэтому использовать в сравнении такие оценки не будем. Хочется усреднить.

Арифметическое усреднение:

Давайте, так как прогрессия геометрическая, попробуем найти среднее геометрическое (такая вот аргументация)

База - метод наименьших квадратов (LS)

Попробуем оценить с помощью МНК. Система уравнений будет иметь вид

Два комментария:

Свободная переменная (номер измеренной точки) не обязательно должна принимать значения: 0, 1, 2, 3, 4. Нам удобнее будет взять симметричный промежуток -2, -1, 0, 1, 2. При этом обозначения , , , , сохраним.
Написанная система уравнений является нелинейной, а для МНК нужна линейность по неизвестным параметрам, поэтому будем логарифмировать систему.

Распишем в векторном виде:

Представим в матричном виде:

Мы специально ранее выбрали симметричный диапазон для чтобы столбцы матрицы системы были ортогональны.

Решением будет:

Третья формула для оценки готова.

Еще одно решение на основе SVD (TLS)

Давайте запишем самые простые оценки по соседним отсчетам в единую систему:

Эти уравнения показывают что вектор пропорционален вектору . Точнее, пропорциональность бы была, если бы не было шума. А так, получается, что каждый вектор случайно смещен относительно своего истинного положения и равенство является приближенным.

Если составить матрицу из этих векторов, то получится матрица ранга 2. В тоже время, если бы шума не было, то ранг матрицы был бы равен 1, так как столбцы пропорциональны друг другу. Таким образом, нужно найти ближайшую матрицу ранга 1 к данной матрице ранга 2.

Два вектора задают плоскость. Нам нужно найти подпространство меньшей размерности (линию на этой плоскости) которая наиболее близка (в смысле перпендикуляра) к обоим векторам. Направление, которое задает эта линия и будем считать тем истинным направлением, которое было бы у этих векторов без шума.

На рисунке показана линия , которую нужно найти как линию, наиболее близкую к двум векторам и .

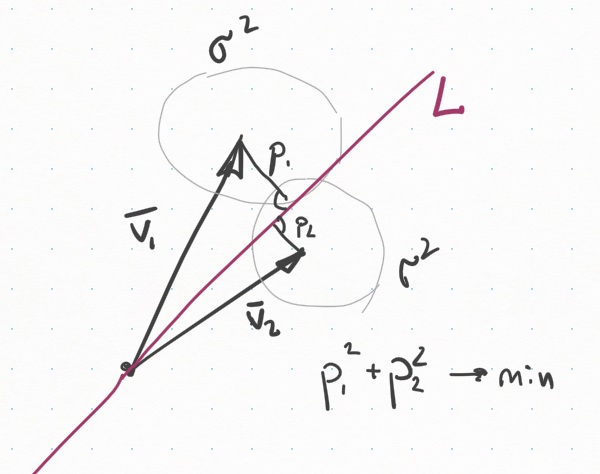
Нахождение ближайшей матрицы меньшего ранга можно сделать через сингулярное разложение (SVD).

К сожалению, даже в таком простом случае (5 дискретных отсчетов) мне не удалось выразить оценку через входные точки. Поэтому последнюю формулу запишем как

ИТОГО: наши претенденты

Напоминаю, у нас есть 5 зашумленных точек геометрической прогрессии. По ним мы пытаемся оценить знаменатель этой геометрической прогрессии. Делаем мы это для того, чтобы устойства, которые измеряют токи в энергосистеме, точнее определяли значение тока и реже ошибочно отключали наши дома.

Мы вывели 4 формулы. Предлагаю на них еще раз посмотреть и проверить интуицию, выбрав одну из них, до того как мы посмотрим результаты численного эксперимента.

Испытания

Проведем 30 000 опытов по генерации зашумленных данных. По мере набора статистики будем оценивать среднее значение знаменателя геометрической прогрессии.

Истинное значение оцениваемого знаменателя - 0.97, СКО шума - 0.01.

using LinearAlgebra

numberOfExp = 30000 #количество экспериментов
realCommonRatio = 0.97 #истинное значение знаменателя
sigma = 0.01
n = 0: 4
y = realCommonRatio.^n

# массивы для графиков
qEstAM = zeros(numberOfExp)
qEstGM = zeros(numberOfExp)
qEstLS = zeros(numberOfExp)
qEstTLS = zeros(numberOfExp)

qEstAMcurrent = zeros(numberOfExp)
qEstGMcurrent = zeros(numberOfExp)
qEstLScurrent = zeros(numberOfExp)
qEstTLScurrent = zeros(numberOfExp)

experiments = 1:numberOfExp

# функции, реализующую каждую из формул
function arithmeticMean(noisedGeomProgr)
    y0, y1, y2, y3, y4 = noisedGeomProgr

    (y1/y0 + y2/y1 + y3/y2 + y4/y3) / 4  
end

function geometricMean(noisedGeomProgr)
    y0, y1, y2, y3, y4 = noisedGeomProgr

    (y4/y0)^0.25    
end

function leastSquares(noisedGeomProgr)
    y0, y1, y2, y3, y4 = noisedGeomProgr

    (y4^2 * y3 / y1 / y0^2)^0.1    
end

function totalLeastSquares(noisedGeomProgr)
    v0 = noisedGeomProgr[1: end-1]
    v1 = noisedGeomProgr[2: end]

    svdResult = svd([v0 v1])
    S = svdResult.S

    #обнуление сингулярного числа, соответствующего шуму
    S[2] = 0
    
    M = svdResult.U * Diagonal(S) * svdResult.Vt
    v0cleared = M[:, 1]
    v1cleared = M[:, 2]

    sqrt((v1cleared'*v1cleared) / (v0cleared'*v0cleared))
end

# Начальные значения переменных, в которых будем копить рассчитанные значения
sAM = sGM = sLS = sTLS = 0

for k in experiments
    # Данные, искаженные шумом с равномерным распределением
    noised_y = y + sigma * ( rand(length(n))*2 .- 1 )
    
    am = arithmeticMean(noised_y)
    gm = geometricMean(noised_y)
    ls = leastSquares(noised_y)
    tls = totalLeastSquares(noised_y)

    qEstAMcurrent[k] = am
    qEstGMcurrent[k] = gm
    qEstLScurrent[k] = ls
    qEstTLScurrent[k] = tls

    sAM += am
    sGM += gm
    sLS += ls
    sTLS += tls

    qEstAM[k] = sAM / k
    qEstGM[k] = sGM / k
    qEstLS[k] = sLS / k
    qEstTLS[k] = sTLS / k
end

Результаты оценки знаменателя

plot(experiments, [qEstAM qEstGM qEstLS qEstTLS],
title="Оценка знаменателя геом. прогр. по мере набора статистики",
ylabel="Значение оценки",
yguidefontsize = 16,
xlabel="Номер эксперимента",
xguidefontsize = 16,
ylims=(0.9695, 0.9705),
label = ["Arithmetic Mean" "Geometric Mean" "Least squares" "TLS"],
legendfontsize=12,
ytickfontsize = 12,
legend=:bottomright,
linewidth = 3)

По графикам видно, что арифметическое усреднение дает худшие результаты. Значение завышено по сравнению с истинным значением и по отношению к другим формулам оценки. Само отклонение невелико, но нас интересует сам факт различия между формулами.

Результаты сравнения стандартного отклонения

Для сравнения стабильности результатов построим гистограммы.

using Statistics
# посчитаем СКО по всем оценкам
stdAM = std(qEstAMcurrent)
stdGM = std(qEstGMcurrent)
stdLS = std(qEstLScurrent)
stdTLS = std(qEstTLScurrent)

# Построим гистограммы
xmin = 0.95
xmax = 0.99
ymax = 6000
plot(
    histogram(qEstAMcurrent, bins=range(0.96, 0.98, length=25), xlims=(xmin, xmax), ylims=(0, ymax), color = :red, title="AM", alpha = 0.6, legend=false),
    histogram(qEstGMcurrent, bins=range(0.96, 0.98, length=25), xlims=(xmin, xmax), ylims=(0, ymax), color = :green, title="GM", alpha = 0.6, legend=false),
    histogram(qEstLScurrent, bins=range(0.96, 0.98, length=25), xlims=(xmin, xmax), ylims=(0, ymax), color = :yellow, title="LS", alpha = 0.6, legend=false),
    histogram(qEstTLScurrent, bins=range(0.96, 0.98, length=25), xlims=(xmin, xmax), ylims=(0, ymax), color = :blue, title="TLS", alpha = 0.6, legend=false),
    layout=(2, 2)
)
annotate!(0.975, 3000, text("std = $(round(stdAM , digits=5))", :left, 16), subplot = 1)
annotate!(0.975, 3000, text("std = $(round(stdGM , digits=5))", :left, 16), subplot = 2)
annotate!(0.975, 3000, text("std = $(round(stdLS , digits=5))", :red, :left, 16), subplot = 3)
annotate!(0.975, 3000, text("std = $(round(stdTLS , digits=5))", :left, 16), subplot = 4)

Результаты оценки стандартного отклонения

Стандартное отклонение характеризует разброс. По гистограммам и посчитанным значениям видно, что самые стабильные показания дает формула (3) - классический метод наименьших квадратов (снизу слева). Видно что и распределение поуже и повыше. Формула (3) - победитель!!

Послесловие

Я ставил на формулу (4) с использованием сингулярного разложения. Даже было обидно, что такая красивая теория не дала лучшего результата по дисперсии.

При реализации алгоритма оценки "в железе" я использовал формулу (2) - геометрическое усреднение, так как она требует меньше ресурсов для расчета и дает схожие оценки.

P.S.

Пара слов в защиту арифметического усреднения: среднее значение это тоже метод наименьших квадратов, когда под данные подстраивается константа. Для обычного МНК дисперсия ошибок должна быть постоянной (иначе нужен взвешенный МНК) и не должно быть корреляций в ошибках (иначе нужен обобщенный МНК). Для величин , , , второе условие не выполняется. При случайном смещении точки вверх, значение дроби сместится также вверх, а значение дроби сместится вниз. Корреляция между соседями точно есть. Если ее учесть, то можно получить результаты схожие с формулой (3) - LS.

Как посчитать знаменатель геометрической прогрессии?

Контекст

Начальная формулировка задачи

Конечная формулировка задачи

Варианты решения

"Нулевое" что приходит в голову

База - метод наименьших квадратов (LS)

Еще одно решение на основе SVD (TLS)

ИТОГО: наши претенденты

Испытания

Результаты оценки знаменателя

Результаты сравнения стандартного отклонения

Результаты оценки стандартного отклонения

Послесловие

P.S.

Тип

Краткое описание

Связанные материалы

Теги

Категории

Языки

Форматы

Уровень

Статус

Опубликовано

Обновлено

Источник