Логотип Engee в полярной системе координат
Вывод графиков в полярной системе координат
В этом примере мы покажем, как вывести график в полярной системе координат для динамической модели Engee.
Полярный график в интерактивном скрипте
Графики в полярной системе координат позволяют увидеть взаимосвязи, которые не видны на графиках в прямоугольной (декартовой) системе координат: получить представление о выраженности некоторого процесса в определенных направлениях в пространстве, или отследить повторяющуюся динамику в рамках какого-то циклического процесса...
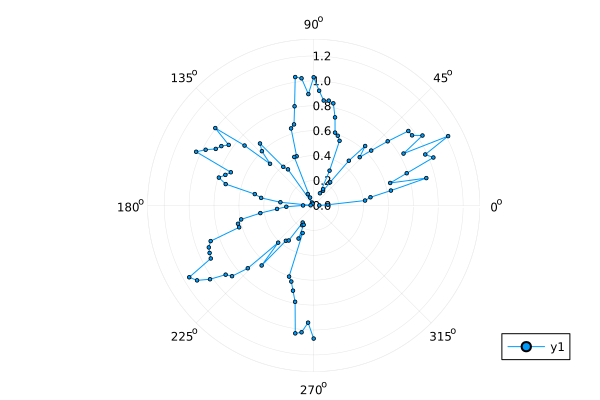
Если работа ведется в интерактивном скрипте Engee, то перевод графика в полярную систему координат осуществляется при помощи аргумента proj. Его значение :polar позволяет нам построить график в полярных координатах:
Θ = range( 0, stop = 1.5π, length = 100 )
r = abs.( 0.1 * randn(100) + sin.(3Θ) )
plot( Θ, r, proj = :polar, m = 2 )
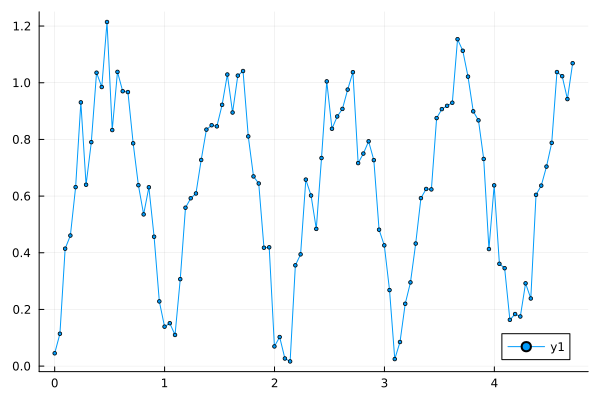
В то время как параметр ortho строит график в прямоугольной системе координат
plot( Θ, r, proj = :ortho, m = 2 )
Попробуем построить график в полярной системе координат, пользуясь только холстом и инструментом вывода графиков для динамических моделей ().
Полярный график для динамической модели
Чтобы построить полярный график для динамической модели, не прибегая к инструментам интерактивных скриптов, нам нужно будет преобразовать векторы из прямоугольной системы координат в полярную систему.
Рассмотрим следующую модель (draw_polar_engee_logo.engee):
Если запустить ее при помощи кнопки , она построит следующий график:
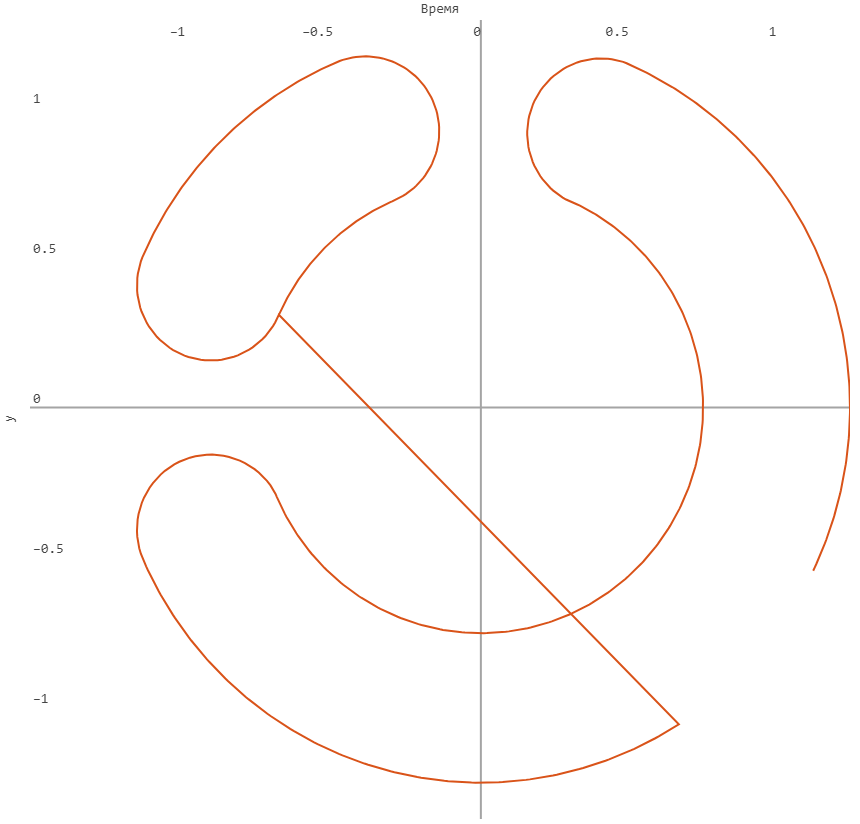
Проанализируем эту модель при помощи средств программного управления моделированием.
modelName = "draw_polar_engee_logo";
model = modelName in [m.name for m in engee.get_all_models()] ? engee.open( modelName ) : engee.load( "$(@__DIR__)/$(modelName).engee");
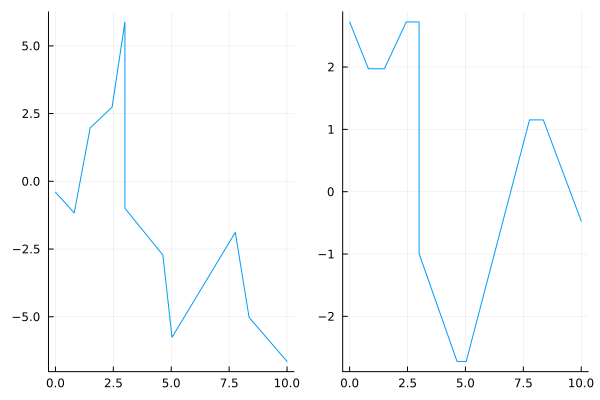
Мы можем изучить, какие кусочно-линейные зависимости заданы в каждом блоке LUT, не запуская симуляцию, а просто обратившись к свойствам каждого блока.
# Анализируем первую таблицу подстановок
x1 = eval(Meta.parse(engee.get_param( modelName*"/LUT1", "BreakpointsForDimension1" )));
y1 = eval(Meta.parse(engee.get_param( modelName*"/LUT1", "Table" )));
# Анализируем вторую таблицу подстановок
x2 = eval(Meta.parse(engee.get_param( modelName*"/LUT2", "BreakpointsForDimension1" )));
y2 = eval(Meta.parse(engee.get_param( modelName*"/LUT2", "Table" )));
# Построим график
plot(
plot( x1, y1, legend=false ),
plot( x2, y2, legend=false )
)
В результате работы, модель строит график в прямоугольной системе координат, но выводит их после преобразования, которое интерпретирует входные сигналы как данные в полярной системе координат.
Выводимый график является суммой двух графиков в полярной системе координат. Первый задает положение центральной линии каждой из двух кривых, составляющий логотип (кривая LUT2, его радиус 1.0). Второй компонент (кривая LUT1, выводимая с радиусом 0.25) моделирует отклонение от центральной линии.
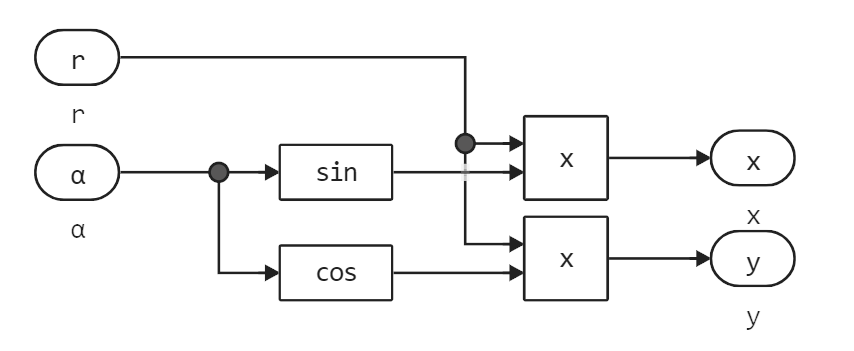
Преобразование координат сделано двумя разными способами. Оба варианта взаимозаменяемы. В первом случае мы преобразуем координаты при помощи простых блоков из базовой палитры:
.png)
Во втором случае мы используем блок Engee Function со следующим кодом, осуществляющим те же операции:
struct Block <: AbstractCausalComponent
# Нет параметров
end
function (c::Block)(t::Real, α, r)
x = r * sin( α )
y = r * cos( α )
return (x,y)
end
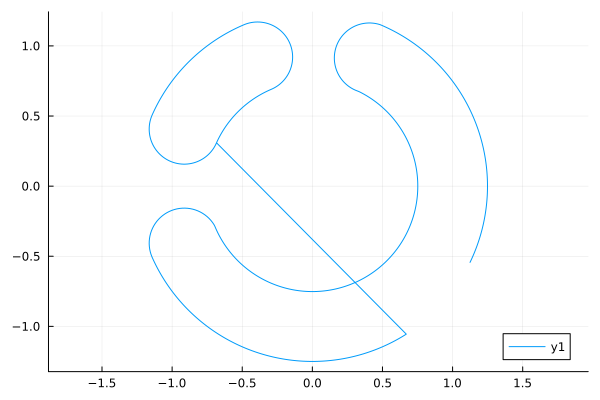
Выведем график, который строит наша модель:
gr()
s = engee.run( modelName, verbose=false );
plot( s["y"].value, s["x"].value, aspect_ratio=:equal )
Заключение
В Engee постепенно появляются всё более сложные инструменты построения графиков, с которыми можно работать не прибегая к программированию.
В этой демонстрации мы показали, как построить график в полярных координатах, не прибегая к программированию и как сделать это используя блок Engee Function.
В отличие от графиков в интерактивном скрипте, графики динамических моделей могут обновляться прямо по ходу симуляции, что создает интересные возможности для интерактивной симуляции моделей.