Малошумящий усилитель

В данном примере мы смоделируем малошумящий усилитель

Коэффициент усиления схемы определяется выражением (R1+R2)/R1 = 101. Моделирование показывает, что системе требуется несколько секунд, чтобы перейти в установившийся режим работы.

Входной сигнал представляет собой синусоиду с амплитудой 0.05 В и частотой 1000 Гц.

Общий вид модели

Рассмотрим модель в Engee (модель LNA.engee):

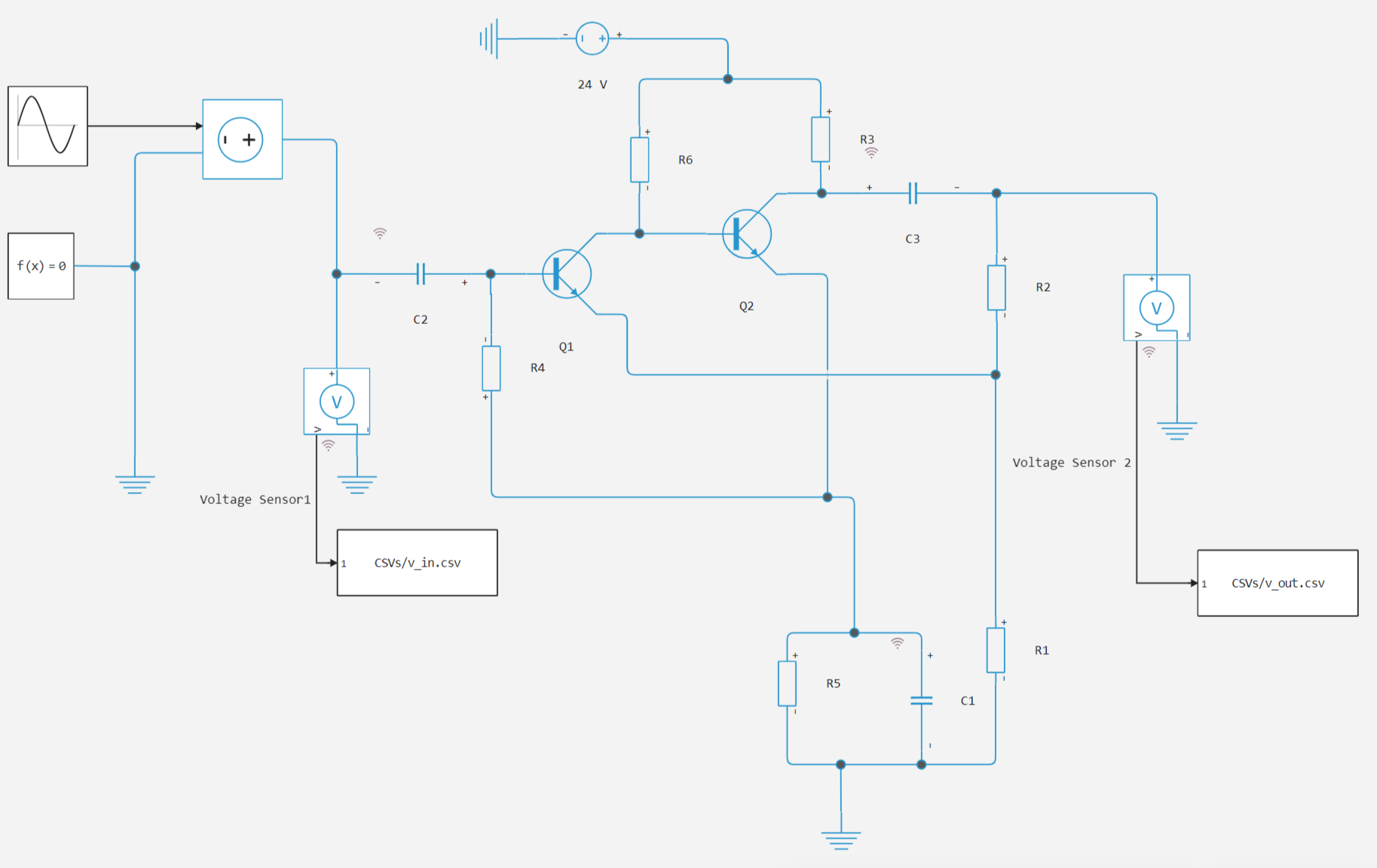
Малошумящий усилитель моделируется с использованием блоков библиотеки электрических компонентов.

Запуск модели с помощью программного управления

Запустить модель можно, открыв непосредственно файл модели LNA.engee и нажав кнопку запуска модели, или с помощью скрипта, как показано ниже.

Переходим в каталог с текущим скриптом:

cd( @__DIR__ ) # Переместимся в каталог, где лежит текущий скрипт
homePath = string(@__DIR__)

"/user/LNA"

Задаем функцию загрузки и запуска модели:

function start_model_engee()
    try
        engee.close("LNA", force=true) # закрытие модели 
        catch err # в случае, если нет модели, которую нужно закрыть и engee.close() не выполняется, то будет выполнена её загрузка после catch
            m = engee.load("$(@__DIR__)/LNA.engee") # загрузка модели
        end;
    try
        global  results = engee.run(m, verbose=true) # запуск модели
        catch err # в случае, если модель не загружена и engee.run() не выполняется, то будут выполнены две нижние строки после catch
            m = engee.load("$(@__DIR__)/LNA.engee") # загрузка модели
            global  results = engee.run(m, verbose=true) # запуск модели
        end
    end

start_model_engee (generic function with 1 method)

Запускаем модель:

    start_model_engee() # загрузка и запуск модели

Building...
Progress 0%
Progress 0%
Progress 0%
Progress 0%
Progress 2%
Progress 7%
Progress 12%
Progress 17%
Progress 22%
Progress 27%
Progress 32%
Progress 37%
Progress 42%
Progress 47%
Progress 52%
Progress 57%
Progress 62%
Progress 67%
Progress 72%
Progress 77%
Progress 82%
Progress 87%
Progress 92%
Progress 97%
Progress 100%
Progress 100%

SimulationResult(
    "C1.n.v" => WorkspaceArray("C1.n.v"),
    "C3.p.v" => WorkspaceArray("C3.p.v"),
    "C2.v_C" => WorkspaceArray("C2.v_C"),
    "C3.i" => WorkspaceArray("C3.i"),
    "C2.p.i" => WorkspaceArray("C2.p.i"),
    "Voltage Sensor 2" => WorkspaceArray("LNA/Voltage Sensor 2"),
    "C2.i" => WorkspaceArray("C2.i"),
    "C1.power_dissipated" => WorkspaceArray("C1.power_dissipated"),
    "C3.v" => WorkspaceArray("C3.v"),
    "C1.v_C" => WorkspaceArray("C1.v_C"),
    "C2.p.v" => WorkspaceArray("C2.p.v"),
    "C3.v_C" => WorkspaceArray("C3.v_C"),
    "C2.power_dissipated" => WorkspaceArray("C2.power_dissipated"),
    "C3.n.v" => WorkspaceArray("C3.n.v"),
    "C1.i" => WorkspaceArray("C1.i"),
    "C3.power_dissipated" => WorkspaceArray("C3.power_dissipated"),
    "C3.n.i" => WorkspaceArray("C3.n.i"),
    "C2.n.v" => WorkspaceArray("C2.n.v"),
    "C2.v" => WorkspaceArray("C2.v"),
    "C3.p.i" => WorkspaceArray("C3.p.i"),
    "C1.n.i" => WorkspaceArray("C1.n.i"),
    "C1.p.i" => WorkspaceArray("C1.p.i"),
    "Voltage Sensor1" => WorkspaceArray("LNA/Voltage Sensor1"),
    "C1.v" => WorkspaceArray("C1.v"),
    "C2.n.i" => WorkspaceArray("C2.n.i"),
    "C1.p.v" => WorkspaceArray("C1.p.v")
)

Перейдем в папку, в которую записались CSV файлы с данными:

cd("/user/CSVs")

Читаем csv-файлы с данными об изменении входного и выходного напряжения на усилителе:

using DataFrames, Plots, CSV # подключение библиотек
v_in = Matrix(CSV.read("v_in.csv", DataFrame)); #входной сигнал
v_out = Matrix(CSV.read("v_out.csv", DataFrame)); #выходной сигнал

Записываем данные о напряжении на конденсаторах:

C1_v = results["C1.v_C"];
C2_v = results["C2.v_C"];
C3_v = results["C3.v_C"];

Визуализация результатов

Выводим график зависимости напряжения от времени на входе и выходе усилителя:

plot(v_out[:,1], v_out[:,2], label="Выходное напряжение") 
plot!(title = "Малошумящий усилитель", ylabel = "Напряжение, В", xlabel="Время, c")
plot!(v_in[:,1], v_in[:,2], label="Входное напряжение")

Из графика видно, что для перехода работы усилителя в установившийся режим необходимо около 4.5 секунд

В установившемся режиме:

v_out_steady_state=v_out[end-200:end,:];#берем только последние 200 точек, для наблюдения работы усилителя в установившемся режиме
v_in_steady_state=v_in[end-200:end,:];
plot(v_out_steady_state[:,1], v_out_steady_state[:,2], label="Выходное напряжение") 
plot!(title = "Малошумящий усилитель", ylabel = "Напряжение, В", xlabel="Время, c")
plot!(v_in_steady_state[:,1], v_in_steady_state[:,2], label="Входное напряжение")

Выводим график зависимости напряжения от времени на конденсаторах:

plot(collect(C1_v)[:,1], collect(C1_v)[:,2], label="C1") 
plot!(title = "Малошумящий усилитель", ylabel = "Напряжение, В", xlabel="Время, c")
plot!(collect(C2_v)[:,1], collect(C2_v)[:,2], label="C2") 
plot!(collect(C3_v)[:,1], collect(C3_v)[:,2], label="C3")

Переход работы малошумящего усилителя в установившийся режим произойдет при окончании зарядки всех конденсаторов.

Заключение

В данном примере мы рассмотрели модель малошумящего усилителя, увеличивающего амплитуду входного сигнала приблизительно в 100 раз, а также построили графики зависимостей входного и выходного напряжения от времени и графики зависимости напряжения на конденсаторах. С помощью графиков мы определили сколько времени требуется для перехода усилителя в установившийся режим работы.

Малошумящий усилитель (LNA)