Метод конечных объемов для уравнения теплопроводности
Решение нестационарного уравнения теплопроводности методом конечных объемов на равномерной струсткуктурированой сетке
Если имеется конечный замкнутый объем V, ограниченый поверхностью S, через которую протекает поток \vec{j}, то, в соответствии с законом сохранения этой величины можно записать
где q - источники
В соответствии с теоремой Остоградского-Гаусса интеграл по контуру в левой части уравнения может быть преобразован в интеграл по объему
Так как это уравнение справедливо для любого объема, то должно выполняться и условие равенства подынтегральных выражений
Расмортим двумерный случай для прямоугольной области (x0, x)х(y0, y). Разобьем расчетную область на nx x ny равномерных, структурированных контрольных обьемов
Уравнение теплопроводности без источников
Проинтегрируем по обьему
Рассмотрим первое слагаемое. Заменим производную разностной схемой, объем - площадью прямоугольной ячейки для двумерного случая
Второе слагаемое. Применим теорему Остроградского и заменим поверхностный интеграл суммой по граням контрольного объема
Воспользуемся нотацией Патанкара и распишем для грани e. Нормаль перпендикулярна к грани и направлена от контрольного объема. Ттогда
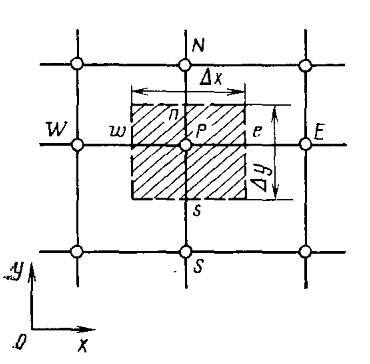
знак нормали в зависимости от грани
Введем обозначение
где F - рассматриваемый сосед с ребром f
Для остальных граней:
n
w
s
Тогда дискретный аналогом исходного уравнения будет
И новое значение температуры в момент времени t+1 в ячейке будет вычислятся по формуле
Из этой записи видно что уравнения для всех объемов можно записать в матричной форме
Где матрица A состоит их коээфициентов Flux_f при T_f и T_P,
\vec{T} вектор искомых значений, \vec{b} вектор коэффициентов не относящихся ни к T_f, ни T_P
Границы
Если на границе задана постоянная температура, тогда в расчетных формулах в дискретном аналоге производной растояние между узлами сократиться в двое и данное слагаемой пойдет в вектор свободных членов
Если на границе задан постоянный поток q, тогда в расчетных формулах подставляем это значение
using SparseArrays, IterativeSolvers
x0 = 0; y0 = 0; x = 1; y = 2; # границы области
nx = 20; ny = 40; # колличество разбиений по x, y
X = range(x0, x, nx);
Y = range(y0, y, ny);
T = zeros(Float32, nx, ny);
# spy(T.==0, markersize=3, markercolor=1)
q = -20;
T0 = 300;
T.=T0;
Tothrs = 300.;
TL = 300.;
T[1, :] .= q*(y - y0) / ny+T0;
T[:, ny] .= q*(x - x0) / nx+T0;
T[nx, :] .= q*(y - y0) / ny+T0;
T[:, 1] .= Tothrs;
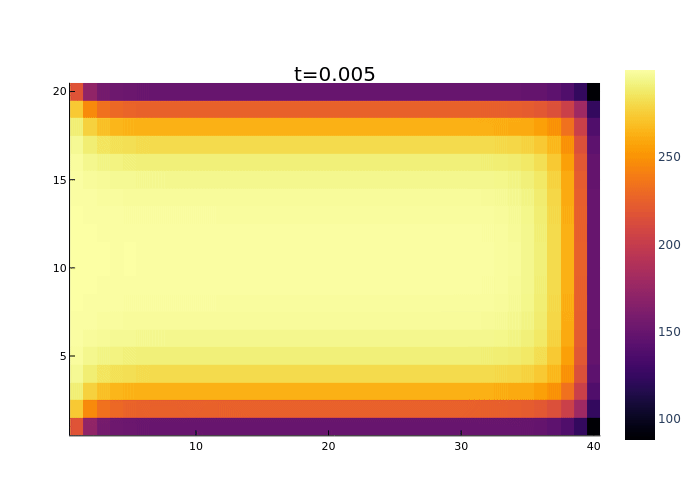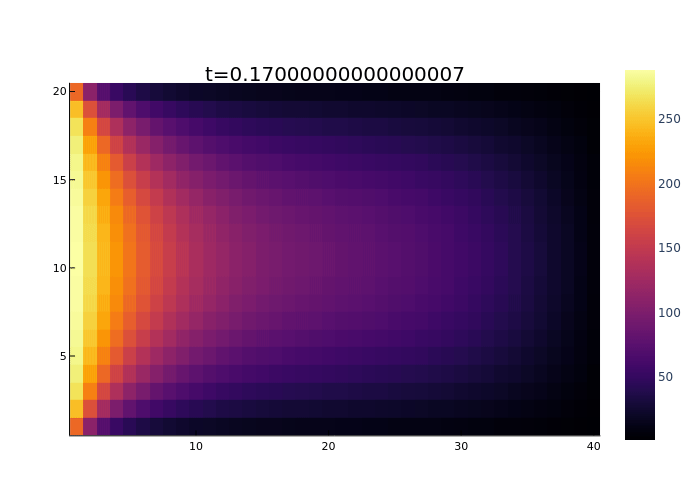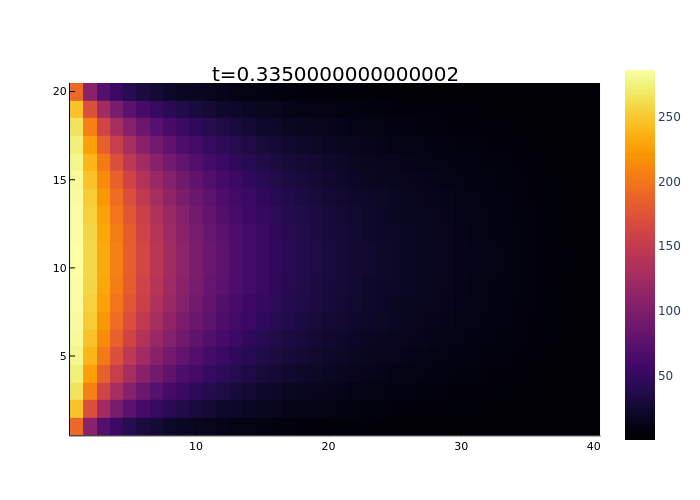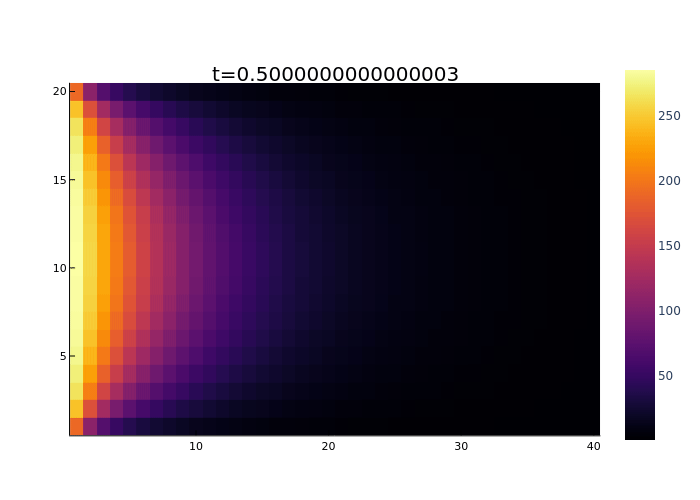
heatmap(T)
let
_dx = (x - x0) / nx; _dy = (y - y0) / ny
# arrays
global res = zeros(Float32,nx*ny)
k = 1.0;
t = 0; t_end = 0.5; dt = (t_end - t) / 100.0;
global anim = @animate while t < t_end
global Is = Array{Int32,1}();
global Js = Array{Int32,1}();
global Values = Array{Float32,1}()
global b = zeros(Float32,nx*ny);
# fill matrix
for j in 1:ny, i in 1:nx
FluxC = 0.0; FluxE = 0.0; FluxW = 0.0; FluxN = 0.0; FluxS = 0.0;
FaceArea = 0.0;
f = 0.0; dx = 0.0; dy = 0.0;
tc = i + (j-1) * nx;
te = 1; tn = 1; tw = 1; ts = 1;
te = tc + 1;
tn = tc - nx;
tw = tc - 1;
ts = tc + nx;
dx = _dx;
FaceArea = _dy; # W
if i == 1 #border
FluxW = q*FaceArea;
# (-k * FaceArea) / dx * 2.;
# f += (k * FaceArea) / dx * 2. * Tothrs;
else
FluxW = (-k * FaceArea) / dx;
end
FluxW *= dt / dx / FaceArea;
dx = _dx;
FaceArea = _dy; # E
if i == nx #border
FluxE = q * FaceArea;
# (-k * FaceArea) / dx * 2.;
# f += (k * FaceArea) / dx * 2. * Tothrs;
else
FluxE = (-k * FaceArea) / dx;
end
FluxE *= dt / dx / FaceArea;
dx = _dy;
FaceArea = _dx; # N
if j == 1 #border
FluxN = (-k * FaceArea) / dx * 2.;
f += (k * FaceArea) / dx * 2. * TL;
else
FluxN = (-k * FaceArea) / dx;
end
FluxN *= dt / dx / FaceArea;
dx = _dy;
FaceArea = _dx; # S
if j == ny #border
FluxS = q*FaceArea;
# FluxS = (-k * FaceArea) / dx * 2.;
# f += (k * FaceArea) / dx * 2. * Tothrs;
else
FluxS = (-k * FaceArea) / dx;
end
FluxS *= dt / dx / FaceArea;
f *= dt / dx / FaceArea;
f += T[i, j];
FluxC = -1 * (FluxE + FluxW + FluxN + FluxS);
FluxC += 1;
# tripletList.emplace_back(tc, tc, FluxC);
push!(Is, tc);
push!(Js, tc);
push!(Values, FluxC);
if te >= 1 && i != nx
# tripletList.emplace_back(tc, te, FluxE);
push!(Is, tc);
push!(Js, te);
push!(Values, FluxE);
end
if tn >= 1 && j != 1
# tripletList.emplace_back(tc, tn, FluxN);
push!(Is, tc);
push!(Js, tn);
push!(Values, FluxN);
end
if tw >= 1 && i != 1
# tripletList.emplace_back(tc, tw, FluxW);
push!(Is, tc);
push!(Js, tw);
push!(Values, FluxW);
end
if ts >= 1 && j != ny
# tripletList.emplace_back(tc, ts, FluxS);
push!(Is, tc);
push!(Js, ts);
push!(Values, FluxS);
end
b[tc] += f;
end
t += dt;
# solve system
global Aw = sparse(Is, Js, Values)
res = IterativeSolvers.cg(Aw,b)
global T = reshape(res,nx,ny)
# animation
heatmap(
# (X),
# (Y),
(T),
# clims=(0,300),
title="t=$(t)"#,
)
end
gif(anim, "heat_t_l_b_anim_TL_$(TL)_Tothrs_$(Tothrs).gif", fps = 10, loop=1)
end