Сообщество Engee
Engee Community
/
Примеры и проекты
/
Многоскоростная обработка с EngeeDSP

Многоскоростная обработка с EngeeDSP

Автор
avatar-ussmoussmo
Notebook

Многоскоростная обработка с EngeeDSP

Многоскоростная обработка сигналов (Multirate Signal Processing) — это область цифровой обработки сигналов (ЦОС), которая занимается системами, где различные части процесса обработки работают на разных частотах дискретизации (ЧД).

Проще говоря, это изменение частоты дискретизации сигнала (количества отсчетов в секунду) внутри цифровой системы. Чаще всего, изменение производится для экономии вычислительных ресурсов (при избыточно высокой частоте дискретизации сигнала), совместимости стандартов (например, аудио 44.1 кГц и 48 кГц), реализации полифазных фильтров и проч.

Основные операции - повышение и понижение частоты дискретизации в целое число раз. Их комбинация позволяет также изменять ЧД в дробное число раз (, где и - целые).

В данном примере мы рассмотрим функции из состава библиотеки EngeeDSP, используемые для задачи повышения ЧД сигнала в 2.5 раза (интерполяции), а также отметим важность применения фильтров нижних частот (ФНЧ) при практической реализации подобных систем.

In [ ]: 
include("helper.jl")                # подключение набора доп. функций

Тестовый сигнал для обработки

В качестве тестового сигнала сгенерируем одну синусоиду основной частоты 100 Гц с частотой дискретизации в 2 кГц. Задача - увеличить частоту дискретизации синусоиды в 2.5 раза, то есть поднять её в 5 раз и затем уменьшить вдвое.

In [ ]: 
fs = 2000;                  # частота дискретизации сигнала
f0 = 100;                   # основная частота повторений синусоиды
dt = 1/fs;                  # шаг временной сетки
t = 0:dt:0.1-dt;            # вектор отсчётов времени
sig = sin.(2*pi*t*f0);      # тестовый сигнал дискретной синусоиды
plot(t, sig, l=:steppost, m=:dot, ms=2, xlim=(0,0.01), legend=false)
Out[0]:

Убедимся, что на спектре есть только одна значимая компонента на частоте 100 Гц:

In [ ]: 
S, fvec = fftspectrum(sig, fs; onesided=true);
plot(fvec, S, legend=false)
Out[0]:

Также обратим внимание на пределы отображения спектра по оси частот - первую зону Найквиста. Она ограничена 1000 Гц.

Повышение частоты дискретизации в 5 раз, понижение в 2 раза

В реальных системах ЦОС нецелесообразно, а зачастую невозможно, применять классические алгоритмы интерполяции. Но для дискретных сигналов можно осуществлять базовые операции над отсчётами, такие как прореживание в целое число раз, или внесение целого числа нулей между отсчётами исходного сигнала. Важно заметить, что при изменении частоты дискретизации в дробное число раз, операция внесения нулей (повышение ЧД) всегда предшествует операции прореживания (понижение ЧД), чтобы не произошла потеря информации. Посмотрим, что произойдёт с формой сигнала и его спектром после описанных базовых операций.

Коэффициент интерполяции

В первую очередь, мы выполняем операцию повышения частоты дискретизации за счёт внесения нулей между отсчётами сигнала. В этом нам поможет функция upsample из библиотеки EngeeDSP. Создадим новый вектор временной сетки с меньшим шагом dtL и отобразим форму сигнала up на временной оси:

In [ ]: 
L = 5;
up = EngeeDSP.Functions.upsample(sig, L);
dtL = 1/(fs*L);
tL = 0:dtL:0.1-dtL;
plot(t, sig, l=:steppost)
plot!(tL, up, l=:steppost, m=:dot, ms=2, xlim=(0,0.01), legend=false)
Out[0]:

Форма исходной синусоиды сильно искажена, и также мы можем наблюдать спектральные копии на расширенной первой зоне Найквиста - от 0 до 5000 Гц:

In [ ]: 
Sup, fvec_up = fftspectrum(up, fs*L; onesided=true);
plot(fvec_up, Sup, legend=false)
Out[0]:

При повышении частоты дискретизации подобным способом, мы расширяем первую зону Найквиста и наблюдаем периодическую структуру спектра дискретных сигналов.

Если мы попробуем проредить подобный сигнал функцией downsample, выкинув каждый второй элемент (коэффициент децимации ), мы получим требуемую частоту дискретизации 2500 Гц, но форма и спектр по-прежнему будут искажены:

In [ ]: 
M = 2;
down = EngeeDSP.Functions.downsample(up, M);
dtM = 1/(fs*L/M);
tM = 0:dtM:0.1-dtM;
plot(tM, down, l=:steppost, m=:dot, ms=2, xlim=(0,0.01), legend=false)
Out[0]:

Из-за алиасинга, мы видим спектральные копии, "завернувшиеся" в результирующую первую зону Найквиста:

In [ ]: 
Sdown, fvec_down = fftspectrum(down, fs*L/M; onesided=true);
plot(fvec_down, Sdown, legend=false)
Out[0]:

Для того, чтобы сохранить форму синусоиды, важно, чтобы в результирующем спектре оставалась только одна составляющая - пик на частоте 100 Гц. Подавить спектральные копии нам поможет цифровой фильтр нижних частот (ФНЧ).

Разработка ФНЧ в интерактивном приложении

Фильтр нижних частот исполняет функцию анти-имаджингового (подавление спектральных копий) при операции повышения частоты дискретизации, а также анти-алиасингового (ограничение верхней границы спектра полезного сигнала) при операции понижения частоты дискретизации.

Спецификация фильтра

Мы знаем, что спектр исходного действительного сигнала ограничен 1000 Гц. Также мы знаем, что ФНЧ применяется после операции внесения нулей, а значит работает на повышенной частоте дискретизации - в нашем случае на 10 кГц. Стоит выбрать форму его АЧХ такой, чтобы полоса пропускания была примерно ограничена 1000 Гц, и в то же время чтобы вне полосы обеспечивалось приличное подавление.

Также стоит учесть и порядок фильтра. Чем он выше, тем ближе форма АЧХ к идеальной (прямоугольной), но большой порядок фильтра вносит большую задержку, а также сложнее реализуем в "железе". Установим следующие требования к нашему ФНЧ:

  • частота дискретизации - 10 000 Гц

  • граница полосы пропускания - 800 Гц

  • начало полосы заграждения - 1500 Гц

  • тип фильтра - КИХ равнопульсирующий

  • пульсации в полосе пропускания - не более 0.1 дБ

  • аттенюация в полосе заграждения - не менее 60 дБ

  • порядок фильтра - минимально возможный для данной спецификации

Приложение "Редактор цифровых фильтров"

Откроем интерактивное приложение "Редактор цифровых фильтров", установим спецификацию фильтра и нажмём кнопку "Синтез фильтра". Мы наблюдаем форму АЧХ, а также порядок синтезированного ФНЧ - 68:

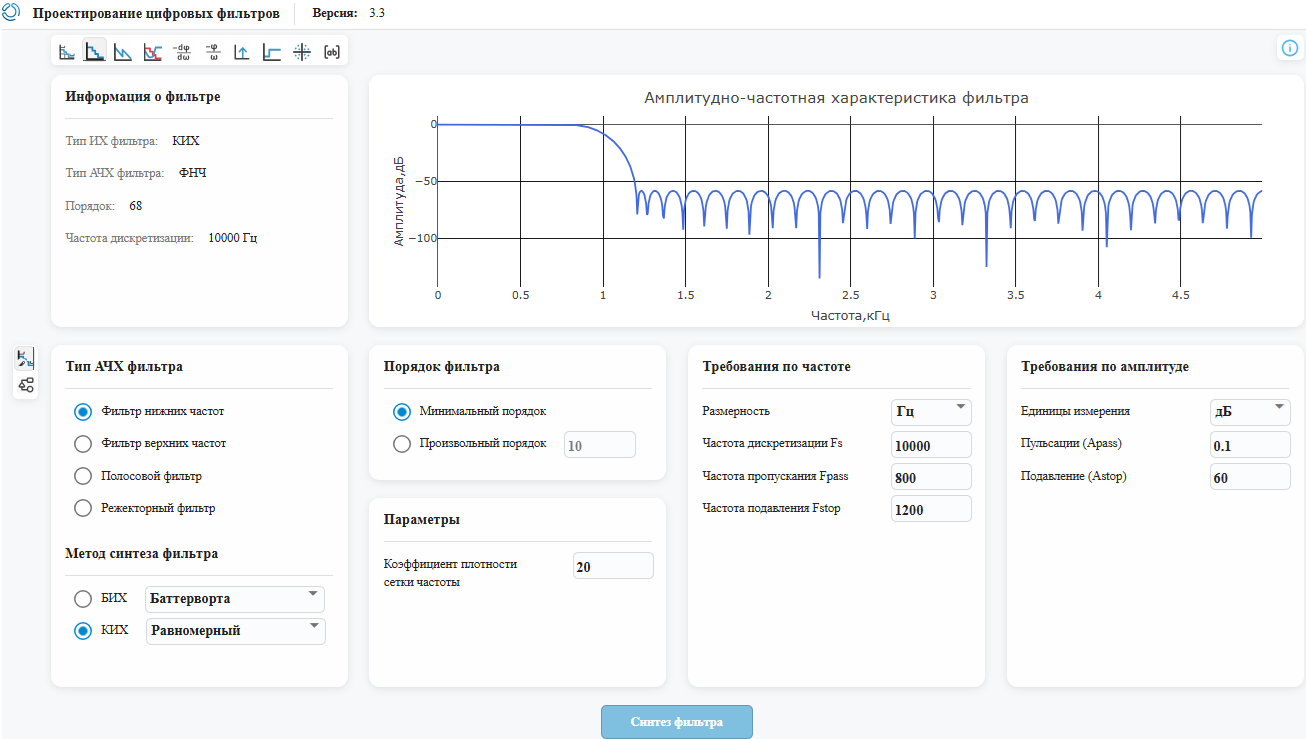
fda.png

Мы можем выгрузить коэффициенты фильтра. Так как мы синтезировали КИХ-фильтр, нас интересуют только коэффициенты числителя его передаточной функции. Мы сохраним их в файл num.txt.

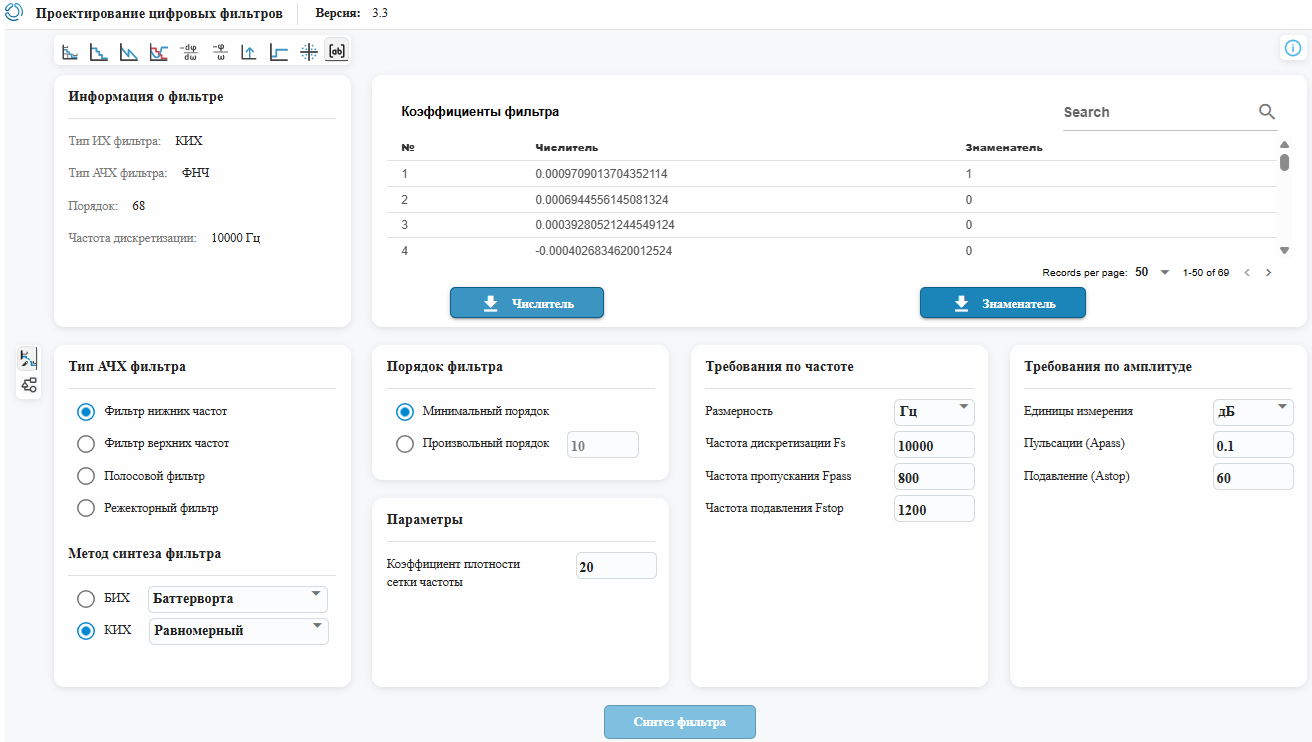
fda2.png

Применим фильтр к сигналу up. Для этого передадим коэффициенты числителя и сигнал на вход функции filter из состава EngeeDSP. Результат фильтрации запишем в переменную up_filtered. Затем проредим этот сигнал функцией downsample, и сохраним результат в переменную decimated.

In [ ]: 
using DelimitedFiles
b = vec(readdlm("num.txt"));
up_filtered = EngeeDSP.Functions.filter(b,1,up) * L;
decimated = EngeeDSP.Functions.downsample(up_filtered,M);
plot(t, sig, l=:steppost, m=:dot, ms=2, xlim=(0,0.02))
plot!(tM, decimated, l=:steppost, m=:dot, ms=2, legend=false)
Out[0]:

Мы видим, что форму синусоидального сигнала удалось восстановить. Во временной области заметна задержка, связанная с применением КИХ-фильтра. Также можно заметить, что результат фильтрации мы умножили на коэффициент интерполяции . Это было необходимо, чтобы не потерять энергетику сигнала, которая уменьшилась после внесения дополнительных нулей.

Убедимся, что спектральные копии в выходном сигнале были успешно подавлены фильтром нижних частот:

In [ ]: 
Sdecim, fvec_decim = fftspectrum(decimated, fs*L/M; onesided=true);
plot(fvec_down, Sdown, legend=false)
plot!(fvec_down, Sdecim, lw=3, ylim=(-80,0))
Out[0]:

Применение специализированных функций интерполяции и децимации

В составе EngeeDSP присутствуют функции interp и decimate, которые выполняют операции повышения и понижения частоты дискретизации вместе с фильтрацией автоматически синтезируемым ФНЧ. Они не вносят задержки, так как применяют фильтрацию с нулевой фазой. Эти функции удобны для анализа и прототипирования, но не отражают поведение реальных последовательных систем ЦОС. Впрочем, из этих функицй в качестве дополнительного выходного аргумента можно извлечь коэффициенты синтезированного КИХ-фильтра нижних частот.

Оценим результат применения функции interp:

In [ ]: 
isig, bb = EngeeDSP.Functions.interp(sig,L);
plot(tL, isig, l=:steppost, m=:dot, ms=2, xlim=(0,0.02), legend=false)
Out[0]:
In [ ]: 
dsig = EngeeDSP.Functions.decimate(isig,M);
plot(t, sig, l=:steppost, xlim=(0,0.02), legend=false)
plot!(tM, dsig, l=:steppost, m=:dot, ms=2)
Out[0]:

Ну и, наконец, отобразим импульсную характеристику рассчитанного автоматически ФНЧ:

In [ ]: 
plot(bb, l=:stem, m=:c, c=6, mc=14, legend=false, title = "ИХ ФНЧ функции interp")
Out[0]:

Эффект алиасинга при понижении частоты дискретизации:

В завершении рассмотрим влияние алиасинга, то есть "заворачивания" спектральных компонент сигнала в первую зону Найквиста при понижении частоты дискретизации до таких значений, когда основное условние теоремы Котельникова уже не выполняется, т.е. когда самая большая частота в спектре сигнала выходит за пределы .

Оценим эффект визуально и на слух на примере синусоидального тона с основной частотой в 2.4 кГц. Меняя значение частоты дискретизации при помощи слайдера, можно наблюдать изменение основной частоты тона при несоблюдении условия теоремы Котельникова. Начиная со значения Гц, тон начнёт понижаться:

In [ ]: 
fs = 6000 # @param {type:"slider",min:3000,max:6000,step:500}
dt = 1/fs;
t = 0:dt:1;
f0 = 2400;
x = sin.(2*pi*f0*t);
S_1, fv_1 = fftspectrum(x, fs; onesided=true);
audioplayer(x,fs)
plot(fv_1, S_1, legend=false, size=(800,200), ylim=(-80,0))
Out[0]:

Заключение

Многоскоростная обработка — это фундаментальный инструмент в ЦОС, который позволяет эффективно управлять частотой дискретизации сигнала для экономии вычислительной мощности, согласования разных цифровых систем, анализа сигналов в разных частотных полосах и повышения качества преобразования. Без неё были бы невозможны современные стандарты связи, аудио- и видеокодеки, а многие вычислительные задачи были бы неоправданно дорогими.

Мы посмотрели, как можно разрабатывать прототипы систем многоскоростной обработки при помощи функций из состава библиотеки EngeeDSP.

Группа видимости
ПубличноПросматривать контент могут все пользователи сообщества

Тип

Интерактивные скрипты

Краткое описание

Изменяем частоту дискретизации сигнала в дробное число раз при помощи функций библиотеки EngeeDSP.

Связанные материалы

Пусто

Теги

Категории

Отраслевые примененияОбработка сигналов

Языки

    Julia

Форматы

    ngscript

Уровень

    Средний

Статус

Опубликовано

Обновлено

Источник

Engee