Julia как инструмент эмпирического анализа моделей Гудвина и Самуэльсона

Вводные соображения

Предворяя свой эмпирический анализ классических моделей эномических циклов, приведу дословно соображения авторов из статьи "Simulation of business and financial cycles: self-oscillation and synchronization"[1].

"Основной интерес при изучении большинства процессов и явлений, рассматриваемых современной наукой, связан с динамическими закономерностями. Динамика современных технических, биологических, социо-экономических систем и процессов обладает исключительной сложностью.Однако, несмотря на сложность, поведение этих систем на достаточно больших отрезках времени определяют сравнительно простые динамические модели и закономерности, такие, в частности, как предельные циклы, торы, странные хаотические аттракторы, метастабильные со-
стояния.
.......
Изучению колебательных экономических и социальных явлений посвящено огромное число публикаций, однако, надо признать, что среди них сравнительно мало публикаций, связанных с разработкой и анализом адекватных математических моделей нелинейной динамики социо-экономических систем. Это можно объяснить рядом причин, в частности, сложностью формального описания социально-экономических явлений, трудностью, а, иногда, невозможностью измерения параметров моделей, трудностями экспериментальной проверки моделей, обуслов-
ленными экстремально большими периодами колебаний и др."

Если с первым тезисом авторов я могу полностью согласится, то второй требует привести собственные соображения, которые и вызвали к жизни эту работу. Моделей, связанных с математическим описанием экономических циклов, известно достаточно много и многие из них появились довольно давно. При этом теоретический анализ для получения практически значимых выводов часто затруднен по целому ряду причин. Появление в последнее время мощного программно-технического инструментария открывает большие возможности для эмпирического исследования и модификации классических динамических моделей экономических циклов.Большая наглядность, возможность варьирования значительного числа параметров, стохастическая иммитация позволяют эмпирически получать важные теоретические и практические результаты.

В данный небольшой работе я хотел показать на известных моделех Гудвина и Самуэльсона, как в принципе можно осуществлять их модификацию и эмпирический анализ, получая при этом очень наглядные результаты.

Модель Гудвина.

Экономические основания модели и ее базовое математическое представление [2]

В основе модели лежат переменные, описывающие производство — Y и потребление — C, связанные между собой соотношением:

                 C=αY +β                     (1)

Константа α характеризует пропорциональность между производством и потреблением
(α < 1), а константа β — потребление в отсутствие производства (охота, собирательство
и т. д.). Еще одна переменная K описывает основной капитал, который включает заводы,
оборудование и т. д. Капитал пополняется в процессе производства, что может быть описано уравнением:

                      Y = C + I             (2)

Здесь переменная I, называемая инвестициями, является производной по времени от величины K (далее мы используем стандартное обозначение для производной по времени) :

                  dK/dt = I.                (3)

Исключая переменную C из уравнений (1) и (2), приходим к уравнению:

                  Y =I +β/1−α               (4)

Два уравнения (3) и (4) связывают три переменные: K,Y и I. Третье уравнение может
быть получено тем или иным способом из основной идеи модели Гудвина о том, что владельцы капитала через посредство изменения инвестиций стремятся управлять капиталом так, чтобы капитал был адекватен производству. Эта адекватность на математическом языке описывается уравнением:

                  K = γY ,                  (5)

где γ — некоторая константа. В общем случае это означает, что инвестиции следует уменьшать при K > Y и увеличивать в случае противоположного неравенства. Кроме того, следует учитывать определенную ограниченность в стремлении управлять капиталом. Даже если ничего не вкладывать в добавление капитала, он уменьшается вследствие амортизации оборудования. Это означает, что величина I ограничена снизу некоторым отрицательным значением Imin. Из общих соображений можно понять, что эта величина также ограничена сверху некоторым значением Imax. Всё это можно написать в виде математического соотношения:

                   I = f (K −γY ),            (6)

где f — некоторая функция, которая удовлетворяет вышеописанным свойствам, то есть уменьшается с увеличением аргумента и ограничена снизу и сверху. Разные виды моделей, возникающие при том или ином способе моделирования функции f , описаны в книге [7]. Для аналитического исследования уравнений, например, удобно моделировать эту функцию в виде скачкообразного изменения в диапазоне от Imin до Imax, так чтобы между скачками значение I было постоянным. Для численных расчетов, когда решается система дифференциальных уравнений, удобны модели с гладкими функциями, конкретный вид которых будет приведен далее.
Из уравнений (3), (4) и (6) следует, что существуют некоторые стационарные значения K0 и Y0, при которых с течением времени все переменные остаются постоянными, причем I0 = 0. Несложные вычисления дают значения:

            Y0 =β/1−α , K0 =γβ/1−α             (7)

Однако, как показывает анализ модели, стационарное состояние является неустойчивым. Если начальное состояние системы характеризуется некоторой точкой вблизи точки стационарного состояния, то с течением времени система отдаляется от стационарного состояния, и начинаются колебания.

Разные виды моделей, возникающие при том или ином способе моделирования функции f , описаны в книге [ ] . Для аналитического исследования уравнений, например, удобно моделировать эту функцию в виде скачкообразного изменения в диапазоне от Imin до Imax так, чтобы между скачками значение I было постоянным. То есть функция f (K −γY ) выбирается в виде:

Для численных расчетов, когда решается система дифференциальных уравнений удобны модели с гладкими функциями f (K − γY ), конкретный вид которых будет приведен далее. Перед проведением численных расчетов следует еще несколько усложнить модель. Из уравнения (4) следует, что изменения инвестиций мгновенно приводят к изменению производства. В реальности изменения производства несколько запаздывают по сравнению с изменениями инвестиций (см. [7]), так что, вместо соотношения (4),
получим:

             Y (t +∆t) = I(t)+β/1−α ,

где ∆t — некоторый малый параметр. Предполагая, что ∆t — малая величина, можно разложить левую часть равенства по степеням ∆t и ограничиться первым членом разложения. В результате получаем уравнение:

        dY(t)/dt ∆t +Y (t) = I(t)+β/1−α     (8)

Аналогично из формулы (6) следует, что изменения величин K и Y мгновенно сказываются на изменении величины I. Однако владельцу капитала необходимо некоторое время ∆t1 для принятия решения об изменении инвестиций. Повторяя аналогичные действия, переходим от уравнения (6) к уравнению:

     dI(t)/dt ∆t1 + I(t) = f(K(t)−γY (t))  , (9)

где ∆t1 — малый параметр. Уравнения (3), (8) и (9) при заданной каким-либо соотношением функции f образуют систему дифференциальных уравнений 1-го порядка, которую можно записать в традиционном виде:

Численное исследование этой системы уравнений затруднено слишком большим числом параметров, которые так или иначе нужно задавать при численном моделировании. Уменьшение числа параметров достигается сдвигом и масштабированием переменных.

После целого ряда преобразований можно получить модель Гудвина в виде следующей системы ОДУ:

Здесь и параметры запаздывания влияния I и K. Для дальнейших расчетов нужно выбрать модель для функции f (K −Y ). Она должна убывать с ростом (K − Y) и обращаться в ноль при нулевом значении этой величины. Кроме того, эта функция должна быть ограничена снизу отрицательным значением −µ/(1+µ) и сверху положительным значением 1/(1 + µ). В качестве f можно использовать функция, за основу которой взята функция arctg(x). Подобная функция содержит два параметра, в качестве которых можно выбрать вышеопределенный параметр µ и параметр λ — модуль тангенса наклона кривой в начале координат. При такой параметризации функция f (K −Y ) принимает вид:

где .

Численное исследование модели (11)

Четыре параметра модели τ,θ,λ и µ имеет довольно ясный смысл. Параметр τ определяет сдвиг по времени между изменением инвестиций и изменением производства.Параметр θ — сдвиг по времени перед принятием решения об изменении инвестиций после анализа состояния системы. Параметр λ — стремление управлять капиталом. Параметр µ — отношение возможной убыли капитала вследствие амортизации оборудования к восстановлению капитала вследствие максимально возможных инвестиций. В соответствии с идеей модели Гудвина, это отношение меньше единицы [7]. Небольшое число параметров позволяет провести некоторое исследование модели на основе численного эксперимента.

В подобных моделях, когда отсутствуют какие-либо соображения по приблизительным величинам параметров и переменных, целесообразно выделить малые параметры, которые положить принимающими значения от 0.1 до 0.9, а остальные параметры положить равными нескольким единицам, или, если параметр по смыслу меньше единицы, — нескольким десятым. Примем простейший набор параметров
τ = θ = 0.7, λ = 3.0, µ = 0.35 и при значениях начальных условий в близи нулевой стационарной точки: K0=Y0=I0=0.01. Разработанный Julia скрипт показал, что, в соотвествии с теорией,исследуемые переменные быстро ререходят в колебательнай режим и их атрактор переходит из начальной точки замкнутый ценр.

Углубленный анализ модели Гудвина.

Рассмотрим модель экономической динамики Гудвина как модель нелинейного акселератора-мультипликатора, которая может быть записана в виде [3]:

где означает доход, предельный уровень потребления, константа представляющая
запаздывание в динамике коэффициента развития, запаздывание между решением об
инвестировании и соответствующими расходами, инвестиции индуцированные
изменениями дохода и Q(t) размер независимых издержек по времени. Обобщенная форма этого уравнения была дана Лоренцем:

здесь – отклонение дохода от равновесия, – четная функция с условиями ;
– нечетная функция с условием , – функция издержек.
В своих исследованиях Лоренца и Нуссэ [4] предложили конкретный вид функций и :

Функцию можно трактовать как некоторое внешнее воздействие. Рассмотрим три случая:
; -некоторая детерминированная переодическая функция; - некоторая стохастическая переодическая функция.

1. Случай

В этом случае модель Гудвина (дифференциальное уравнение второго порядка) можно привести к системе дифуров 1-го порядка:

В этой системе существуют три равновесия , , .

Равновесие зависит от всех трех параметров. Исследуем эту зависимость. Исходя из экономического смысла параметров: определяет предельный уровень потребления при соотвествующих значениях и ; - норма потребления; -коэффициент снижения дохода, чем он меньше тем больше доход. Зададим следующие значения: ; ; .
Проведем соответствующие расчеты с помощью разработанного нами скрипта Julia (см. ниже).

Как видно из графиков, в восьми исследованных точках пространства параметров a,b,c мы нашли две точки (2.0,0.25,0.2) и (2.8,0.25,0.20), в которых система из переходит в колебательный режим (аттрактор седло). В остальных исследуемых точках система переходит в устойчивое состояние (аттрактор устойчивый фокус).Если детально исследовать пространство параметров (задать небольшой шаг по каждому параметру,то можно найти точки биффуркации,где система переходит из одного состояния в другое). Например, если в найденных точках параметров, где система находится в колебательном режиме, мы начнем увеличивать значение параметра ,то система перейдет в устойчивое состояние (точка биффуркации)

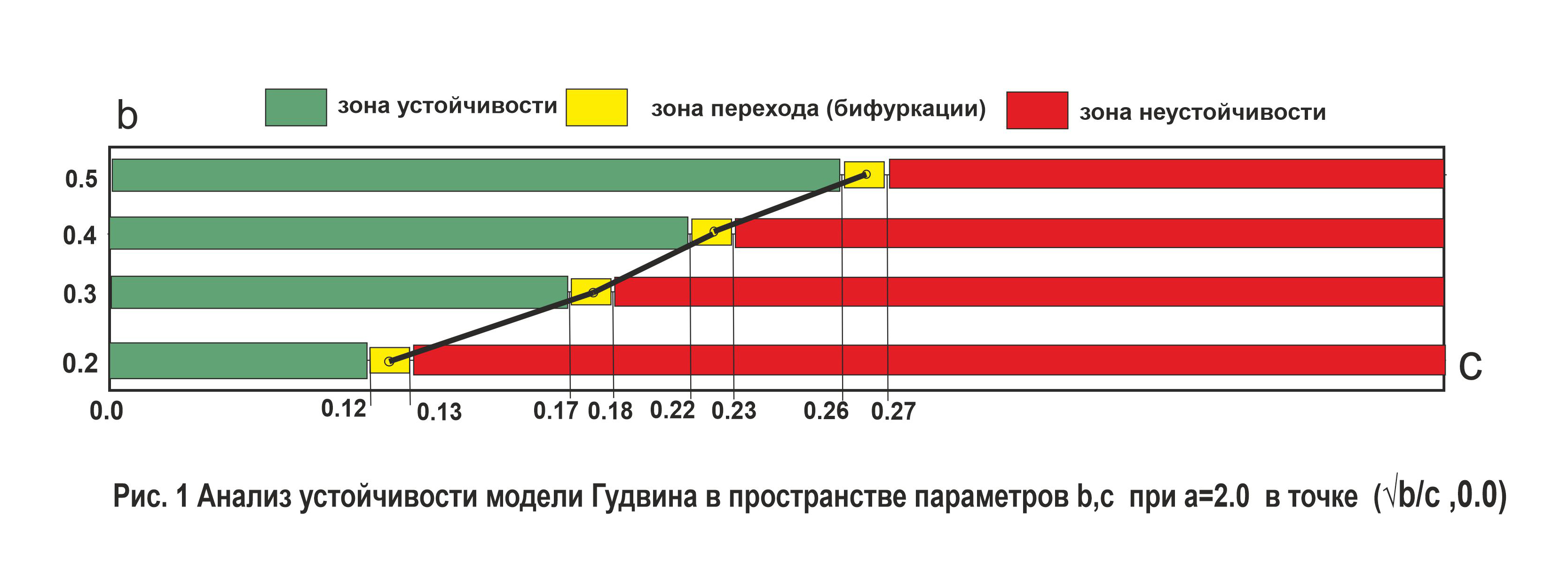
Перейдем к анализу устойчивости модели Гудвина в точке . Зададим и посмотрим как изменяется поведение системы в пространстве параметров . При этом, из экономических сображений набор значений параметра представим как вектор ,а значения параметра будем определять эксперементально двигаясь от значения параметра вниз с шагом 0.01 с тем, чтобы обнаружить точку бифуркации, где система переходит из одного состояния в другое. Ниже с помощью разработанных нами скриптов, мы получили для каждого значения параметра серии из 4-х графиков, демонстриющих переход системы из устойчивого состояния в колебательный режим.Полученные результаты можно представить в виде графика(рис. 1). На графике видны точки бифуркации (желтые квадраты),соединяя которые можно получить линию бифуркации.Она делит пространство значений параметров на области устойчивых и неустойчевых состояний.

2. Случай детерминированная переодическая функция

Пусть внешнее воздействие Q(t) это переодическая функция вида:

где -частота; -фаза; - амплитуда;
- уровень относительно которого происходят колебания.

1. Зададим такие параметры Q(t),при которых она на соотвествующем диапозоне t будет возрастающей функцией. Обеспечить (возрастание функции) можно задав fr=0.02 и faz=10.0. Обеспечить условие Q(t)>0 (экономически это означает наличие внешнего притока средств в экономику) можно выбрав определенное значения и и соотношение между ними.

Пусть множество значений параметра A1 представляет собой вектор [5.0,10.0,20.0,30.0,40.0,50.0,60.0,70.0] (отношение изменяется от 0.1 до 1.4). Ниже представлен скрипт, который строит серию графиков для каждого значения

Из графиков видно, что угол наклона Q(t) увеличивается от arctg(2/30)=3.81 град. до arctg(25/30)=39.81 град. То есть, скорость роста Q(t) увеличивается на интервале исследования более чем в 10 раз. Функция сначала стабилизируется на определенном уровне, а затем переходит в режим практически линейного устойчивого роста, при этом переходная фаза к усточивому состоянию становиться все менее выраженной (уменьшается число колебаний и их амплитуда). Грубо по графикам оценим скрость роста . При ; ; ; ;
; ; . В точке, где кривая роста стновитья явно выпуклой и это последняя точка, где на всем диапозоне исследования (). В точке и уходят в отрицательную зону и движение становиться хаотичным. Точкой бифуркации является точка расположенная между и . Это хорошо видно по фазовым портретам последних двух точек исследования.

2. Зададим такие параметры Q(t),при которых она на соотвествующем диапозоне t [0,100] будет убывающей функцией. Обеспечить (убывание функции) можно задав fr=0.02 и faz=0.0. При этом на исследуемом инттервале времени функция может и (экономически это означает наличие убывающего притока средств в экономику, переходящего в отток ресурсов из экономики ).Данное поведение можно обеспечить, выбрав определенное значения и и соотношение между ними.

Пусть множество значений параметра A0 представляет собой вектор [100.0, 50.0, 40.0,35.0] (отношение изменяется от 1.0 до 0.35). Ниже представлен скрипт, который строит серию графиков для каждого значения

Из графиков видно, что по мере движения от значения отношения до система деградирует (x(t) падает) со все увеличивающейся скоростью, а между точками 0.4 и 0.35 она коллапсирует и разрушается

3. Зададим такие параметры ,при которых она на соотвествующем диапозоне t [0,100] будет переодической функцией (). При этом на исследуемом инттервале времени функция может и (экономически это означает наличие переодически увеливающегося и убывающего притока средств в экономику, переходящего в определенные моменты t в отток ресурсов из экономики).Данное поведение можно обеспечить, выбрав определенное значения и и соотношение между ними.

Пусть множество значений параметра A0 представляет собой вектор [200.0, 10.0, 2.0] (отношение изменяется от 0.025 до 2.5). Ниже представлен скрипт, который строит серию графиков для каждого значения

Из графиков видно, что при значении отношения система сохраняет устойчивое состояние(x(t)≈ 9.2 ).При находится в колебательном режиме с частотой близкой к частоте $Q(t).\text{При} система переходит в сложное состояние с переодической составляющей с постоянным переходом в отрицательную зону,с экономической точки зрения это соотвествует коллапсу и разрушению системы (фазовый портрет седло с петлями).

Q(t) стохастическая функция

Используем в качестве Q(t) переодическую функцию, в которой вносятся случайеые положительные возмущения в частоту и aмплитуду. Ниже представлен скрипт, который генерирует реализаций подобной функции

Статистический анализ Q(t)

На множестве,состоящем из реализаций , в каждом временном сечении сформирована случайная величина, то есть имеется система из T случайных велечин (в нашем случае T=20). В скрипте определяются среднее (mean),среднеквадратичное отклонение (std) и коэффициет вариации (Cv) для каждой случайной величины q(t),t=1:20. На этой основе строятся графики:mean(t),mean(t)+3std(t),mean(t)-3std(t) и Cv(t). Из графиков видно, что в 99% реализаций Q(t) находятся в интервале [0.0,105.0]. Минимум коэффициета вариации min Cv = 18.32 %, а максимум max Cv=32.55. Посмотрем как Q(t) c такими статистическими характеристиеами влияет на x(t) и каков при этом фазовый портрет, порождаемый моделью Гудвина