Модель передискретизированного сигнала OFDM

В данном примере мы рассмотрим модель передискретизированного сигнала OFDM (Orthogonal frequency-division multiplexing, технология цифровой модуляции с использованием большого количества близко расположенных ортогональных поднесущих, или мультиплексирование). Модель позволяет увидеть связку нескольких модуляций. Еще в данном примере используется блок RMS, измеряющий сигнал с модуляцией OFDM и с наложенным на него шумом, масштабированным по значению, пропорциональному числу активных поднесущих относительно размера FFT (Fast Fourier transform, Быстрое преобразование Фурье), чтобы подтвердить, что мощность сигнала приблизительно равна единице.

Модель строится по следующему принципу.

1. Генерируются случайный целочисленный набор данных и пилотные входные символы.
2. 16-QAM модулирует данные и пилотные символы.
3. OFDM модулирует QAM-модулированный сигнал. Пара модуляторов и демодуляторов OFDM обрабатывает три символа с разными индексами поднесущих пилот-сигнала и длинами циклического префикса для каждого символа. Сигнал OFDM содержит данные и пилоты, которые модель генерирует с частотой, в четыре раза превышающей частоту дискретизации.
4. Далее накладываем аплитудное искажение на каждый кадр, что значительно меняет мощность сигнала.
5. После чего OFDM демодулирует и раздельно выводит данные и пилоты.
6. 16-QAM демодулирует данные и пилотные символы.
7. После этого находим разницу между входом и выходом.

На рисунке ниже показана реализованная модель.

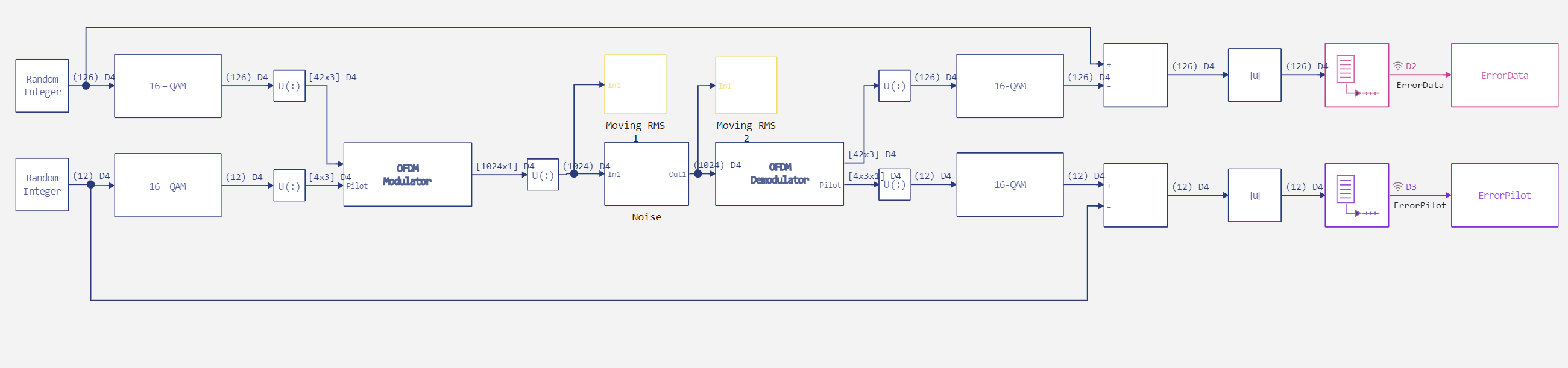
Далие выполним инициализацию параметров модели.

M = 16;              # Порядок модуляции
nfft = 64;           # Длина FFT
NumSymbols=3;        # Количество символов OFDM
osf=4;               # Фактор передискретизации
ngbc = [9;8];        # Число носителей защитного диапазона
insertdcnull = true;  # Наличие DC-нулевой поднесущей
addpilotport = true;  # Присутствие пилота
Noise_power = 10; # Мощность шума

# Индексы пилотных поднесущих
pscindx = [[12;26;40;54] [14;28;38;52] [12;26;40;54]]; 
cplen = [16; 32; 16];  # CyclicPrefixLength
# Выборки на кадр для данных
spf_data = NumSymbols * (nfft-sum(ngbc)-size(pscindx,1)-insertdcnull)
# Выборки на кадр для пилота    
spf_pilot = NumSymbols * size(pscindx,1)
# Число активных поднесущих
nasc = nfft-sum(ngbc)+insertdcnull;

После объявления параметров модели выполним инициализацию функции запуска модели и запустим саму модель.

# Подключение вспомогательной функции запуска модели.
function run_model( name_model)
    
    Path = (@__DIR__) * "/" * name_model * ".engee"
    
    if name_model in [m.name for m in engee.get_all_models()] # Проверка условия загрузки модели в ядро
        model = engee.open( name_model ) # Открыть модель
        model_output = engee.run( model, verbose=true ); # Запустить модель
    else
        model = engee.load( Path, force=true ) # Загрузить модель
        model_output = engee.run( model, verbose=true ); # Запустить модель
        engee.close( name_model, force=true ); # Закрыть модель
    end
    sleep(5)
    return model_output
end

run_model("OFDM_Signal_and_QAM") # Запуск модели.

Building...
Progress 0%
Progress 0%
Progress 0%
Progress 3%
Progress 8%
Progress 13%
Progress 18%
Progress 23%
Progress 28%
Progress 33%
Progress 38%
Progress 43%
Progress 48%
Progress 54%
Progress 59%
Progress 64%
Progress 69%
Progress 74%
Progress 79%
Progress 84%
Progress 89%
Progress 94%
Progress 99%
Progress 100%
Progress 100%

Dict{String, DataFrame} with 4 entries:
  "ErrorPilot" => 121×2 DataFrame…
  "RMSout"     => 10241×2 DataFrame…
  "ErrorData"  => 1261×2 DataFrame…
  "RMSinp"     => 10241×2 DataFrame…

Теперь проведём анализ записанных даднных.

ErrorData = collect(ErrorData);
ErrorPilot = collect(ErrorPilot);
RMSinp = collect(RMSinp);
RMSout = collect(RMSout);

ErrorData = ErrorData.value;
ErrorPilot = ErrorPilot.value;
RMSinp = RMSinp.value;
RMSout = RMSout.value;

plot([real(RMSinp),real(RMSout)], title="RMS", label=["До наложения шума" "После наложения шума"])

Как мы видим, мощность сигнала варьируется от кадра к кадру. Теперь посмотрим на разницу между входным и выходными данными.

plot([ErrorData,ErrorPilot], title="Разница между входами и выходами", label=["Данные" "Пилоты"])

Судя по графику, ошибка нулевая, но чтобы убедиться в этом, найдём суммарную ошибку.

println("Суммарная разница между входными и выходными данными: " * string(sum(ErrorData)))
println("Суммарная разница между входными и выходными пилотами: " * string(sum(ErrorPilot)))

Суммарная разница между входными и выходными данными: 0.0
Суммарная разница между входными и выходными пилотами: 0.0

Вывод

В данном примере мы разобрали и продемонстрировали возможности применения нескольких типов модуляций в системах связи. Этот подход очень востребован в данной сфере деятельности.