Модель ракеты с системой самонаведения
nkapyrin
azasentaМодель ракеты с системой самонаведения¶
Покажем, как добавить в модель ракеты модель системы самонаведения, которая будет срабатывать при детектировании цели и приводить объект управления в нужную точку в пространстве.
Модель динамики объекта¶
Объект управления представляет собой ракету нормальной аэродинамической схемы с крыльями в середине и рулями в хвостовой части.
Основная часть модели объекта - нелинейное представление динамики жесткого тела (блок 3DOF (Body Axes)). Аэродинамические силы и моменты, действующие на корпус ракеты, рассчитываются на основе коэффициентов, которые представлены нелинейной зависимостью как от скорости Маха, так и от угла атаки. Эти функции хранятся в модели в табличном виде, в блоках 2-D Lookup Table.
В модели также используются такие блоки из палитры "Аэрокосмические системы" как, например, модель стандартной атмосферы, которые являются общими для всех аэрокосмических систем.
Описание модели планера¶
Динамическая модель планера состоит из четырех основных подсистем и автопилота, который управляет нормальным ускорением ракеты через перемещение руля. Подсистема Атмосфера, Угол атаки и Воздушная скорость рассчитывает влияние атмосферных условий в зависимости от высоты полета. Подсистемы Привод руля и Датчики связывают модель автопилота с моделью планера. Блок Аэродинамические силы и Модель движения рассчитывает силы и моменты, действующие на корпус ракеты, а затем рассчитывает модель движения.
Атмосфера и воздушная скорость¶
В этой модели используется стандартный блок ISA Atmosphere Model - модель стандартной атмосферы по ISA (МСА). В дополнительных блоках рассчитывается скорость (в Мах) с использованием текущей скорости звука, а также скоростной напор Q.
Аэродинамические силы и коэффициенты¶
В подсистеме Аэродинамические силы происходит расчет сил и моментов, приложенных к ракете, в осях корпуса. Затем происходит интегрирование уравнений движения, определяющих линейное и угловое движение объекта управления.
Аэродинамические коэффициенты хранятся в табличной форме, а мгновенные значения во время моделирования определяются при помощи интерполяции.
Модель автопилота¶
Автопилот ракеты управляет рулем высоты исходя из заданного нормального ускорения. Акселерометр размещен ближе к носу ракеты, впереди от центра тяжести. Его сигнал, с дополнительным демпфированием, используется для формирования сигнала управления.
Коэффициенты автопилота были подобраны на основе нескольких линеаризованных моделей планера, полученных для разных условий полета в ожидаемом диапазоне. В модель также входит и канал для управления по сигналу насыщения (anti-windup), чтобы предотвратить насыщение регулятора при выходе сигнала автопилота за пределы допустимых значений.
Созданный таким образом автопилот мы тестируем в представленной в этом проекте нелинейной модели.
Контур наведения¶
За нахождение и ведение цели отвечают две подсистемы:
- Поиск/Слежение - возвращает оценку текущих параметров относительного движения между ракетой и целью
- Наведение - рассчитывает желаемое нормальное ускорение в режиме преследования и желаемый угол визирования в режиме поиска
Вычислитель системы наведения¶
Эта подсистема выдает сигналы управления для разных систем:
- сигнал самоликвидации, когда с момента захвата цели прошло больше обозначенного времени,
- заданный угол визирования в режиме поиска цели,
- фиксированную команду на нормальное ускорение в режиме "слепого полета" (финальный режим),
- собственно, режим работы системы,
- сигнал снятия системы с предохранителя.
Латинские названия, как правило, нужны как компромисс для корректной работы генератора кода.
Вычислитель управляет работой всех бортовых систем через переменную Mode (внешняя переменная Режим). Эта переменная отвечает за переключение режимов управления. Во время поиска цели вычислитель напрямую управляет углом линии визирования, отправляя сигнал Sigma_d на подвес антенны. Когда цель находится в радиусе захвата луча искателя (сигнал Acquire или Захват), система отрабатывает заданную паузу, а затем переходит в режим слежения в замкнутом контуре. При возможной потере захвата система сперва переходит в режим поиска, а спустя обозначенное время происходит самоликвидация.
Первый конечный автомат выдает команды управления для перемещения и слежения, а также передает второму автомату сигнал id_timeout при превышении допустимого времени преследования после потери цели:
Второй автомат выдает сигнал снятия с предохранителя при приближении цели (если система находится в режиме RadarGuided или при превышении времени ожидания.
Пропорциональное управление в режиме слежения¶
После того как искатель захватит цель и вплоть до столкновения (или самоликцидации) для управления ракетой используется пропорциональный закон управления. Такой закон управления вычисляет желаемое нормальное ускорение на основе следующих данных:
- измерение скорости сближения ракеты и цели, которые можно получить с помощью допплеровского устройства слежения, если головка самонаведения оснащена радиолокационным оборудованием,
- оценка скорости изменения угла линии визирования (скорость сканирования).
Подсистема слежения¶
Эта подсистема осуществляет обнаружение и слежение за целью, управляет ориентацией антенны и удержанием ее на цели согласно закону управления. Постоянная времени контура слежения tors равна 0.05 секунд, его настройка позволяет выставить баланс между желаемой скоростью реакции и устойчивости к шумам. Контур стабилизации отвечает за поправку скорости смещения луча антенны для учета угловой скорости корпуса. Его коэффициент выбран исходя из полосы пропускания гироскопа.
На выходе система кроме переменных состояния выдает оценку угловой скорости цели - сглаженную сумму скорости перемещения луча антенны и скорости изменения угла антенна-цель, полученной от радара. Полоса пропускания фильтра равна половине полосы пропускания автопилота.
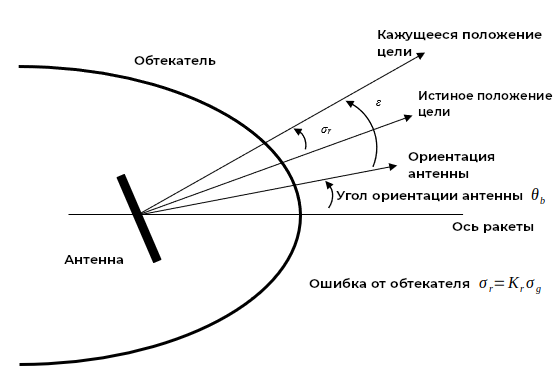
Погрешность обтекателя¶
Для ракет с радиолокационным наведением обычным источником погрешностей является обтекатель, влияющий на задержку приема и диаграмму направленности. Как правило, величина этой погрешности вычисляется по нелинейной функции, принимающей на вход угол ориентации антенны. Наша модель аппроксимирует это влияние линейной зависимостью между углом ориентации антенны (Gimbal) и величиной искажения при помощи коэффициента "Погрешность от обтекателя".
В этой подсистеме можно реализовать модели других важных погрешностей, например влияние перегрузок на работу гироскопов. Эти модели позволят проверить надежность регуляторов контура слежения и стабилизации.
Запуск и демонстрация работы системы¶
Теперь запустим модель на исполнение. В ее Обратных вызовах заданы такие исходные параметры:
- цель движется с постоянной скоростью 328 м/с по встречному курсу
- цель находится на 500 м ниже точки пуска антенны
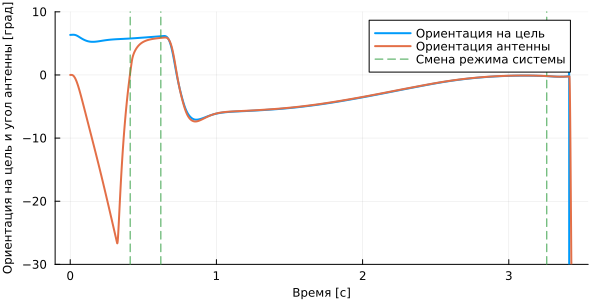
Результат показывает, что захват происходит спустя 0.42 с после пуска, затем на отметке 0.63 система переходит в режим слежения, а столкновение произошло на отметке 3.27 с.
model_name = "aero_guidance";
model_name in [m.name for m in engee.get_all_models()] ? engee.open(model_name) : engee.load( "$(@__DIR__)/$(model_name).engee");
res = engee.run( model_name );
Отделим нужные сигналы:
Mach_speed = collect(res["Атмосфера, Угол атаки и Воздушная скорость.Скорость (Мах)"]);
sigma_antenna = collect(res["Слежение и оценка скорости сканирования.Ориентация антенны"]);
sigma_target = collect(res["Ориентация на цель.1"]);
sigma_rad = collect(res["Sigma_rad"]);
alpha = collect(res["Incidence & Airspeed.α"]);
mode = collect(res["Вычислитель системы наведения (100 Hz).Режим"]);
misile_traj = collect(res["Планер и Автопилот.Xe,Ze"]);
target_traj = collect(res["Положение цели.Цель"]);
Az = collect(res["Аэродинамические силы и Модель движения.Ax,Az"]);
Az_d = collect(res["Az_d.1"]);
fin_demand = collect(res["Автопилот.Заданное положение руля"]);
fin_position = collect(res["Привод руля.B"]);
model_stop = collect(res["Подрыв.Остановка"]);
Построим графики переменных состояния и визуализируем траектории:
gr()
plot(
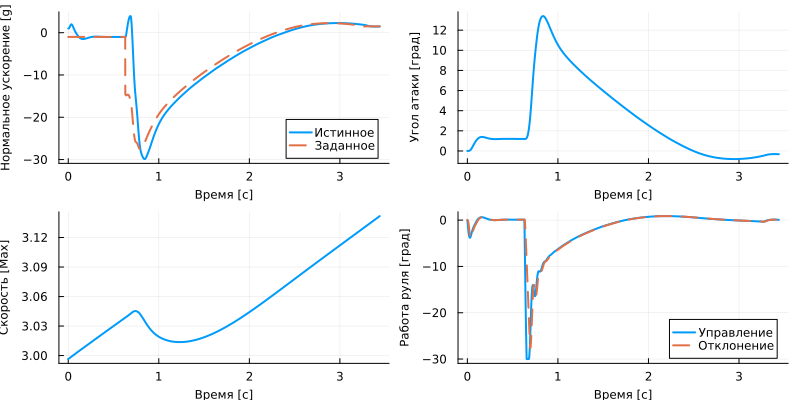
plot( Az.time, [last.(Az.value) Az_d.value]./9.81, ls=[:solid :dash], ylabel="Нормальное ускорение [g]", label=["Истинное" "Заданное"], xlabel="Время [c]" ),
plot( alpha.time, rad2deg.(alpha.value), ylabel="Угол атаки [град]", xlabel="Время [c]", leg=false ),
plot( Mach_speed.time, Mach_speed.value, ylabel="Скорость [Мах]", xlabel="Время [c]", leg=false ),
plot( fin_demand.time, rad2deg.([fin_demand.value fin_position.value]), ls=[:solid :dash], ylabel="Работа руля [град]", label=["Управление" "Отклонение"], xlabel="Время [c]" ),
guidefont=font(8), lw=2, size=(800,400)
)
mode_change_idx = findall( diff(mode.value).>0 )
plot( sigma_target.time, rad2deg.(sigma_target.value), label="Ориентация на цель", ylimits=(-30,10), lw=2 )
plot!( sigma_antenna.time, rad2deg.(sigma_antenna.value), label="Ориентация антенны", ls=[:solid :dash], lw=2 )
vline!( [mode.time[mode_change_idx]], ls=:dash, label="Смена режима системы" )
plot!( guidefont=font(8), lw=2, size=(600,300), xlabel="Время [с]", ylabel="Ориентация на цель и угол антенны [град]" )
# Приведение разных сигналов к одному времени интегрирования
sample_time_factor = length(first.(target_traj.value)) / length(model_stop.value)
f_idx = 1:round(Int, findfirst(model_stop.value .> 0)*sample_time_factor)
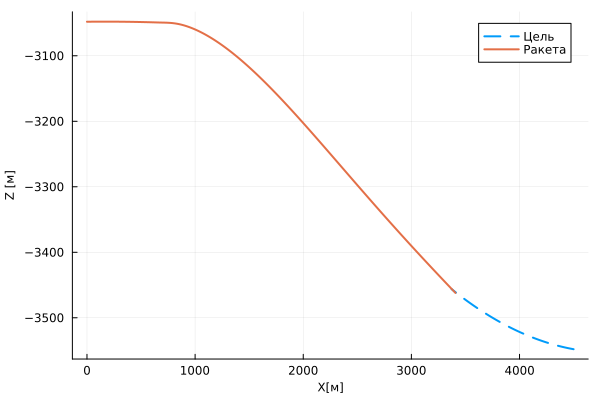
plot( first.(target_traj.value)[f_idx], last.(target_traj.value)[f_idx], label="Цель", lw=2, ls=:dash )
plot!( first.(misile_traj.value)[f_idx], last.(misile_traj.value)[f_idx], label="Ракета", lw=2 )
plot!( guidefont=font(8), size=(600,400), xlabel="X[м]", ylabel="Z [м]" )
Теперь модель легко запустить для любого набора входных условий и изучить ее работу.
Заключение¶
Мы реализовали сравнительно сложную модель системы наведения ракеты на цель и проследили ее траекторию.
[2] Лебедев А.А., Чернобровин Л. С. Динамика полета беспилотных летательных аппаратов. М. – 1973.