Модель скорости ветра для анализа работы ветроустановок

Существует проблема, связанная с корректным компьютерным и физическим моделированием работы ветроустановок на реальных ветрах. Это особенно важно для ветроустановок малой и средней мощности, которые работают с ветрами невысокой среднегодовой скорости и значительной турбулентности.

Скорость ветра может быть смоделирована как нестационарный случайный процесс, созданный наложением двух компонент, низкочастотной компоненты - v_s(t) и турбулентной компоненты - v_t(t):

Поведение этих компонент может быть продемонстрировано спектральной моделью Ван Дер Ховена [1], работа которой представлена на рисунке 1:

Рисунок 1 - Спектральная модель Ван Дер Ховена

Согласно рисунку 1 наименьшая спектральная плотность мощности для низкочастотной компоненты приходится на диапазон от 2-ух часов до 10-и минут. Это означает, что интервал времени в течении которого низкочастотная компонента может оставаться неизменной на уровне среднего равен 10 минутам.

Математическое описание динамических особенностей турбулентной компоненты v_t(t) может быть осуществлено с помощью спектра Каймала [2]. Этот спектр дает математическое описание зависимости спектральной плотности колебаний от их частоты:

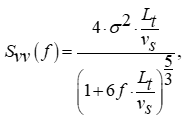
где S_vv - спектральная плотность мощности колебаний,  σ - среднеквадратичное отклонение скорости ветра, L_t - длина турбулентности,
v_s - среднее значение низкочастотной компоненты, которое сохраняется в течении 10 минут, f - частота колебаний.

Среднеквадратичное отклонение скорости ветра σ может быть рассчитано через параметр интенсивности турбулентности I_t по формуле:

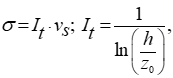
где h - высота над землей, z₀ - коэффициент шероховатости земной поверхности (z₀ = 0.01 - ровная поверхность, 0.1 - небольшие препятствия, 1 - городская местность).

Длина турбулентности рассчитывается согласно формуле:

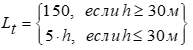
На рисунке 2 представлена спектральная функция по вышеописанным формулам:

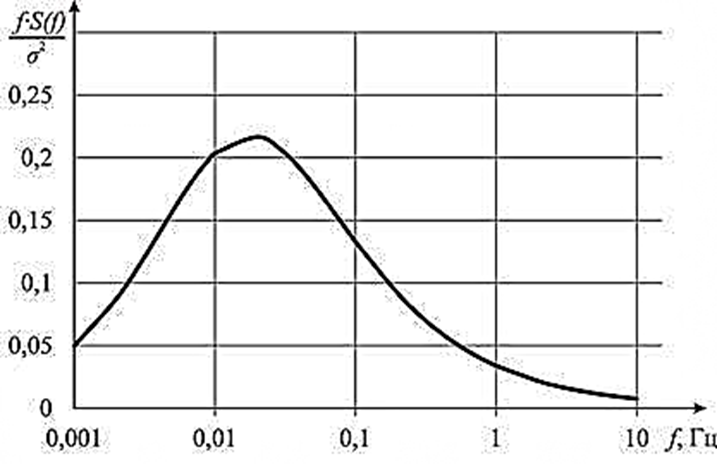
Рисунок 2 - Спектральная функция Каймала при h = 30 м, z₀=0.01, v_s=10м/с

Опираясь на спектральную функцию возможно создать модель, которая будет отображать поведение турбулентной составляющей скорости ветра на протяжении 10 минутного интервала времени, пока низкочастотная компонента скорости ветра будет оставаться постоянной величиной. Данная модель показана ниже:

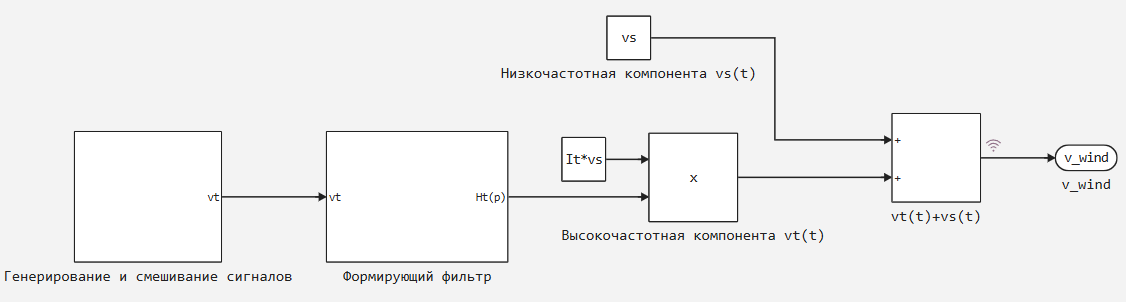
Модель основана на смешивании косинусоид с разными значениями амплитуды, частоты и фазы. Смешанный сигнал проходит через формирующий фильтр и корректируется согласно с величиной среднеквадратичного отклонения преобразуясь таким способом в значение турбулентной компоненты. Турбулентная компонента в свою очередь добавляется к постоянному значению низкочастотной компоненты v_s. Таким образом на выходе модели получаем величину скорости ветра на протяжении 10-ти минутного интервала времени.

Смешивание косинусоид осуществляется согласно формуле:

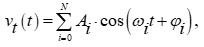
где A_i - значение амплитуды, которое рассчитывается согласно формуле

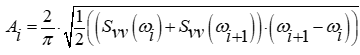
w_i - значение частоты, которое отвечает диапазону Гц, φ_i - значение фазы которое находится в диапазоне [-π;π] и генерируется случайным образом.

Постоянная времени T_f и коэффициент усиления K_f формирующего фильтра:

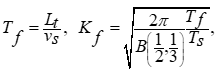
где B - бета-функция, T_s - период дискретности для турбулентной функции (принимается равным приблизительно 10-ти минутам).

Передаточная функция формирующего фильтра:

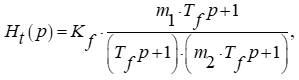
где m₁ = 0.4; m₂ = 0.25.

Поведение скорости ветра согласно приведенным выше принципам было смоделировано в среде Engee :

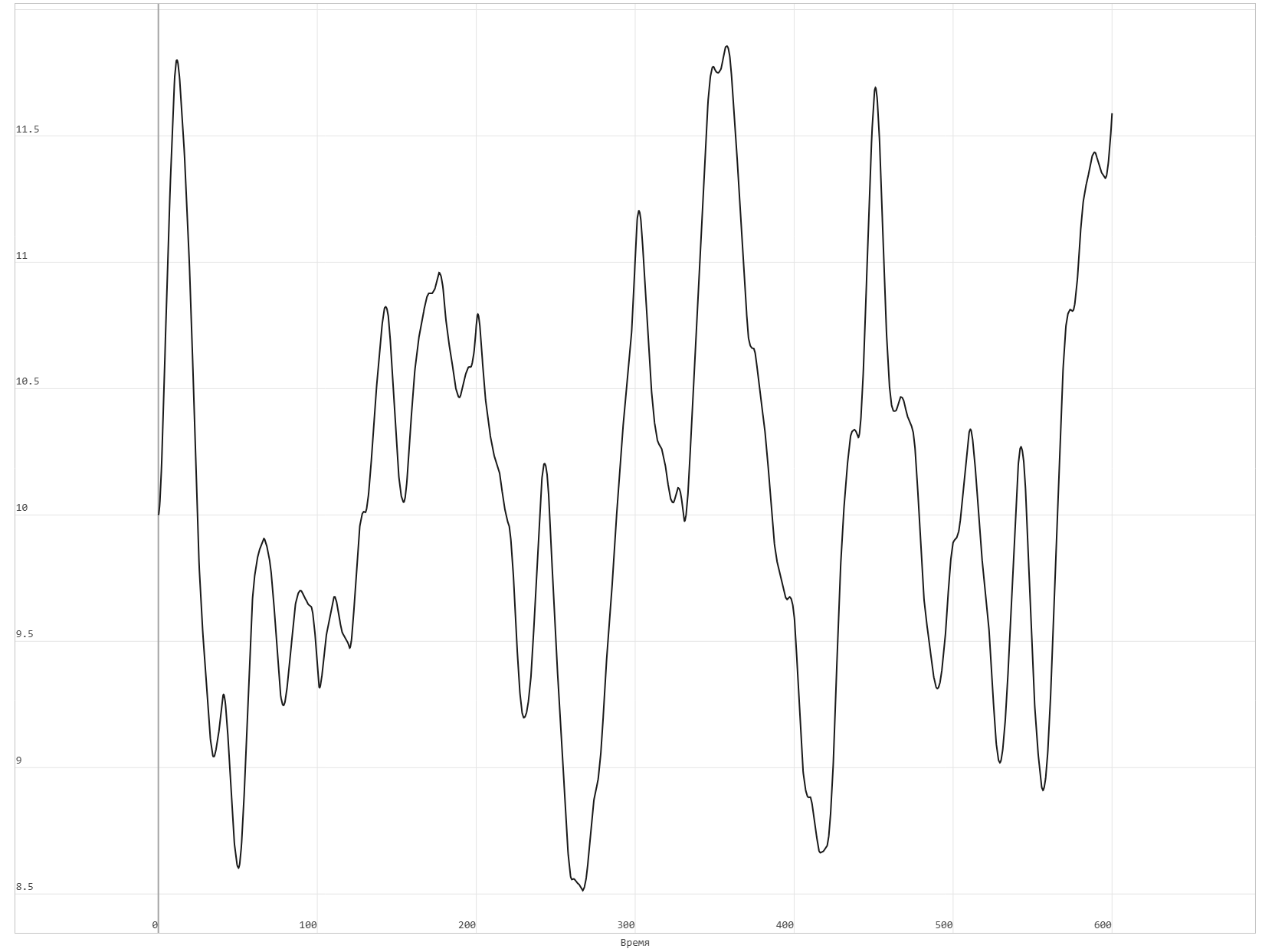
Репозиторий состоит из двух основных компонентов:

1. Инициализационный скрипт с настройками и исходными данными

2. Модель Engee для симуляции поведения ветра

Важно: Перед запуском модели необходимо выполнить инициализационный скрипт для корректной установки всех параметров.

Список литературы:

1. Van der Hoven, I. (1957). "Power Spectrum of Horizontal Wind Speed in the Frequency Range from 0.0007 to 900 Cycles Per Hour." Journal of Meteorology, Vol. 14, No. 2, pp. 160-164.

2. Kaimal, J.C., Wyngaard, J.C., Izumi, Y., and Coté, O.R. (1972). "Spectral characteristics of surface-layer turbulence." Quarterly Journal of the Royal Meteorological Society, Vol. 98, No. 417, pp. 563-589.