Модели экономического роста на Julia и Engee
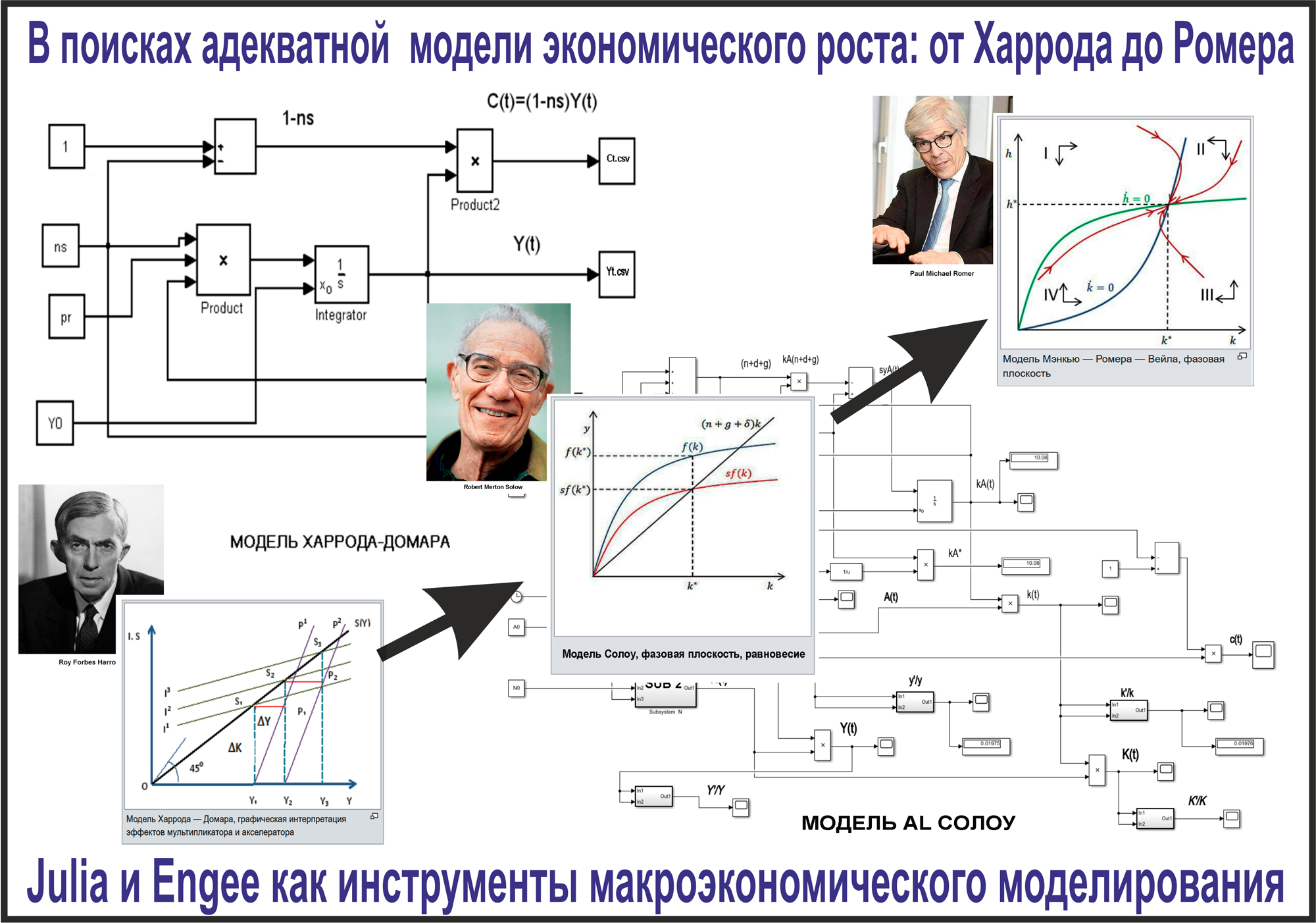
Математические модели экономического роста.
ИССЛЕДОВАНИЕ МОДЕЛИ Р. ХАРРОДА - Е. ДОМАРА.
1.1 Дискретная модель Р.Харрода-Е.Домара.
Исходные постулаты
Модель построена на следующих постулатах:
- Рассматривается односекторная закрытая экономика без государства;
- Эндогенные факторы инвестиции I и прирост капитала ΔK;
- Экзогенные факторы s =const –норма сбережения и σ=const средняя про-
изводительность капитала (НТП отсутствует); - Сбережения считаются равными инвестициям, а инвестиции равны при-
росту капитала в следующий период времени (I=ΔK); - Модель функционирует в соответствии со следующей экономической
логикой:
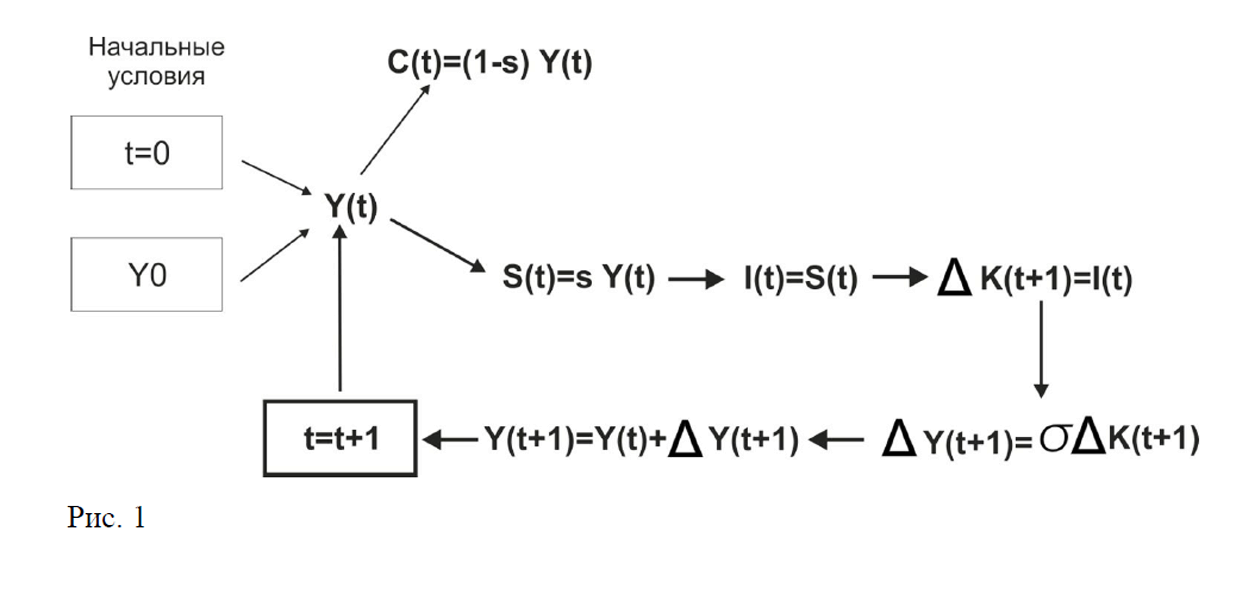
Здесь Y(t) –объем выпуска в год t; S(t) – сбережения в год t; I(t) – инвестиции в год t; ΔK(t+1) прирост капитала в год t+1; ΔY(t+1)- прирост выпуска в год t+1; Y(t+1)- объем выпуска в год t+1, С(t)- потребление в год t.
Базовые соотношения и свойства
-
S(t)=sY(t)
-
I(t)=S(t)
-
ΔK(t+1)=I(t)
-
ΔY(t+1)= σΔK(t+1)
Из (1-4) имеем :
Здесь - мультипликатор,
- акселератор.Таким образом, темп прироста объема предложения в модели Харрода постоянен и равен произведению нормы сбережения на среднюю производительность капитала (мультипликатор) или частному нормы сбережения и акселератора.
Оценим, каким должны быть темпы прироста потребления и инвестиций в модели, чтобы рост предложения был равновесным и устойчивым.
Модель дополняется соотношением Кейнса:
Y(t) = S(t)+C(t), где C(t)- (потребление) (6)
Покажем, чему должен быть равен темп прироста спроса при выполнении условий 1-4,6.
Из уравнения 6 получаем:
S(t) = Y(t) − C(t) (7)
Используя уравнения 1-4 и 7, получаем:
ΔY(t+1)= σ(Y(t) − C(t) )=σsY(t) (8)
Из 8 получаем:
C(t) = Y(t)(1 − s) (9)
Аналогично получаем:
C(t+1) = Y(t+1)(1 − s) (10)
Вычитаем из (10) ( 9) получаем:
ΔC(t+1) = ΔY(t+1)(1 − s) (11)
Поделим обе части уравнения (11) наC(t) получим:
Из (12) и (9) имеем:
После преобразований получаем:
Следовательно :
Таким образом, устойчивый равновесный рост экономики при полном использовании капитала в модели Харрода обеспечивается тогда, когда темпы прироста предложения, потребления и инвестиций совпадают и равны .
При этом экономика растет по экспоненте с показателем степени . Роль государства состоит в создании условий для обеспечения равновесия между спросом и предложением, равенства инвестиций и сбережений и обеспечения полного использования инвестиций для наращивания капитала.
using Plots, PlotThemes
using StatsBase
#ДИСКРЕТНАЯ МОДЕЛЬ ХАРРОДА-ДОМАРА
#ЗАДАНИЕ ИСХОДНЫХ ДАННЫХ
#горизонт прогноза
T=10
#норма сбережения
s=0.6;
#производительность капитала
a=0.8;
σ=1/a
#начальное значение
b1=zeros(T+1)
b2=zeros(T + 1)
b3=zeros(T + 1)
Y = zeros(T+1)
C = zeros(T+1)
Inv = zeros(T+1)
ΔK = zeros(T+1)
t = 1;
#Расчет эндогенных переменных модели для t=1
#выпуск
Y[t] = 20.0
#потребление
C[t] = (1.0-s)*Y[t];
#инвестиции
Inv[t] = s*Y[t];
#прирост капитала
ΔK[t+1] = Inv[t];
Y[t+1] = Y[t] + σ*ΔK[t+1];
b1[t] = σ * ΔK[t+1] / Y[t];
b2[t]=((1.0-s)* Y[t+1]-C[t])/C[t];
b3[t]=(s*Y[t+1]-s*Y[t])/Inv[t];
for t in (1:T)
C[t] = (1 - s) * Y[t]
Inv[t] = s*Y[t]
ΔK[t+1] = Inv[t]
Y[t+1] = Y[t] + σ * ΔK[t+1]
b1[t] = σ * ΔK[t+1] / Y[t]
b2[t] = ((1.0 - s)*Y[t+1]-C[t]) / C[t]
b3[t] = (s*Y[t+1] - s*Y[t]) / Inv[t]
end
println("Темпы прироста предложения, потребления и инвестиций совпадают и равны σ*s")
println(b1[1:T])
println(b2[1:T])
println(b3[1:T])
t =1:T
theme(:dao)
plot(t, Y[1:T], title="Y , C , I ", ylabel="Y,C,I", xlabel="t", label="Объем производства", lw=2)
plot!(t, C[1:T], label="Спрос", lw=3)
plot!(t, Inv[1:T], label="Инвестиции", lw=2, wsize=(700, 400))
1.2 Непрерывная модель «Р.Харрода-Е.Домара»
Рассмотрим, как выглядит модель в непрерывном времени. Из уравнения (5) имеем:
Переходя к бесконечно малым приращениям, получаем основное дифференциальное уравнение модели Харрода-Домара в непрерывном времени:
Решение этого уравнения имеет следующий вид:
Ниже представлен скрипт численного решения дифференциального уравнения (17) в точках пространства mσ X ms, где
mσ ={1.2,1.4,1.6}; ms ={0.4 ,0.6,0.8} множество значений соотвественно параметров σ и s.
using DifferentialEquations, Plots, PlotThemes
using StatsBase
function harrod!(du, u, p, t)
σ,s = p
du[1]= σ*s*u[1]
end
u0 = [20.0]
tspan = (0.0,3.0)
theme(:dao)
plot(wsize=(800, 500))
#План 'эксперимента по σ
mσ = (1.2:0.2:1.6)
#План эксперимента по s
ms = (0.4:0.2:0.8)
n=length(mσ) * length(ms)
Ymean =zeros(n,3)
k=0
#План 'эксперимента по σ
for i in (1:3)
σ = mσ[i]
#План эксперимента по s
for j in (1:3)
s = ms[j]
p = (σ, s)
prob = ODEProblem(harrod!,u0,tspan, p)
sol = solve(prob,reltol=1e-8, abstol=1e-8)
plot!(sol, linewidth=3, label="σ= $σ s= $s")
k=k+1
Ymean[k, 1] = σ
Ymean[k, 2] = s
Ymean[k, 3] =mean(sol[:, :])
end
end
xlabel!("Time (t)")
ylabel!("Y(t)")
title!("Семейство графиков по модели Харрода Y(0)= $u0")
Эта же задача решена средствами визуального моделирования на платформе Engee
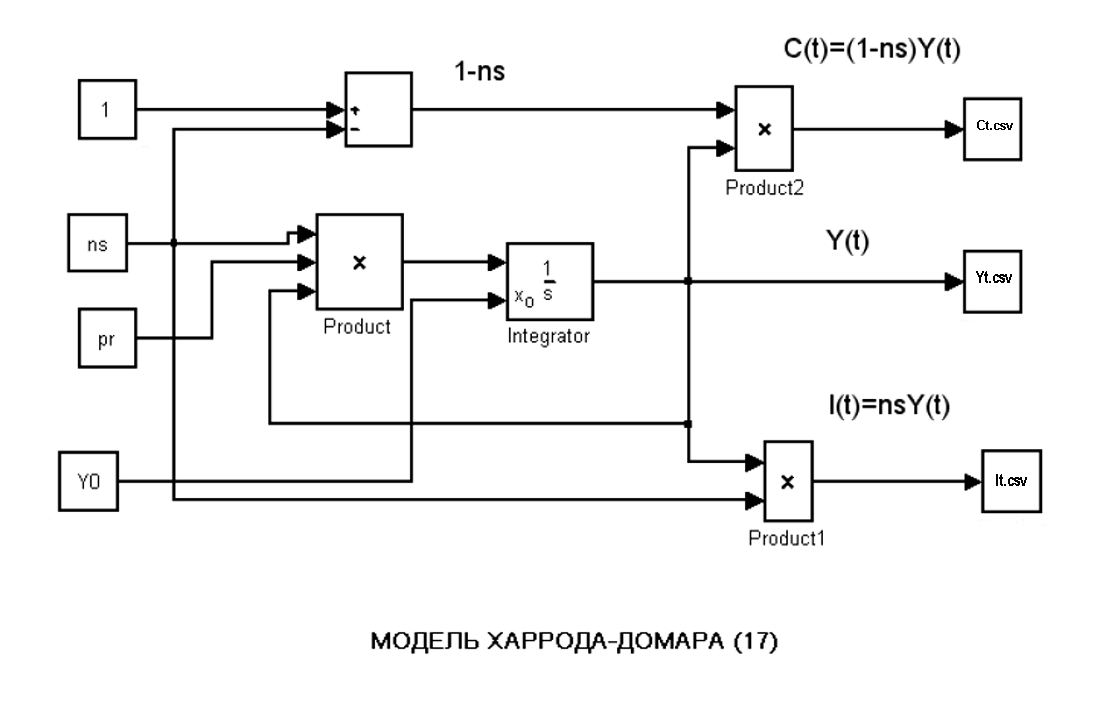
using RDatasets, Plots, PlotThemes
using CSV, DataFrames
#открытие модели
modelName = "Harrod01";
PID_model = modelName in [m.name for m in engee.get_all_models()] ? engee.open(modelName) : engee.load("/user/ModRost/$(modelName).engee");
engee.set_param!(modelName, "StopTime" => 10.0) # интервал моделирования
#Программа исследования непрерывной модели ХАРРОДА
#НОРМА СБЕРЕЖЕНИЯ-nc И МУЛЬТИПЛИКАТОР-pr
nc = 0.55
pr = 1.2
#Начальная ЗНАЧЕНИЕ ДОХОДА - Y0
Y0 = 20.0
#Выполнение модели
engee.run(modelName)
# ВЫДЫЧА РЕЗУЛЬТАТОВ МОДЕЛИРОВАНИЯ
#engee.get_results("Harrod01")
#modeling_variable = engee.get_results("Harrod01")
df_out1 = CSV.read("out1.csv", DataFrame)
df_out2 = CSV.read("out2.csv", DataFrame)
df_out3 = CSV.read("out3.csv", DataFrame)
#ГРАФИКИ
plotly()
theme(:ggplot2)
plot(df_out1[!, "time"], df_out1[!, "1"], label="Ct", legend=:outerbottomright, wsize=(800, 500), linewidth=3)
plot!(df_out2[!, "time"], df_out2[!, "1"], label="Yt", linewidth=3)
plot!(df_out3[!, "time"], df_out3[!, "1"], label="It", linewidth=3)
xlabel!("t")
ylabel!("Объем - доход Yt, инвестиции It, потребление Ct")
title!("Модель Харрода-Домара")
Ниже представлен скрипт, который строит график зависимости среднего объёма производства от значений нормы сбережения и производительности капитала.
using DifferentialEquations, Plots, PlotThemes
using StatsBase
function harrod!(du, u, p, t)
σ, s = p
du[1] = σ * s * u[1]
end
u0 = [20.0]
tspan = (0.0, 3.0)
#План 'эксперимента по σ
mσ = (1.0:0.02:2.0)
#План эксперимента по s
ms = (0.0:0.02:1.0)
n = length(mσ) * length(ms)
Ymean = zeros(n, 3)
k = 0
#План 'эксперимента по σ
for i in (1:length(mσ))
σ = mσ[i]
#План эксперимента по s
for j in (1:length(ms))
s = ms[j]
p = (σ, s)
prob = ODEProblem(harrod!, u0, tspan, p)
sol = solve(prob, reltol=1e-8, abstol=1e-8)
k = k + 1
Ymean[k, 1] = σ
Ymean[k, 2] = s
Ymean[k, 3] = mean(sol[:, :])
end
end
plotly()
theme(:dao)
scatter(Ymean[:, 1], Ymean[:, 2], Ymean[:, 3], legend=false, wsize=(1000, 650), ms=1, ma=0.8, mc=:green)
xlabel!("σ -производительность К")
ylabel!("s-норма сбережения")
zlabel!("Ymean")
title!("Средний объем производства в зависимости от σ и s")
Исследуем непрерывную модель с точки зрения влияния характера изменения потребления на экономический рост.
а. Потребление отсутствует, весь доход тратиться на накопление
Эта гипотеза нереалистична, но позволяет дать оценку максимально возможного для данной экономики темпа роста доходов. Здесь имеем s=1, тогда из (18) получаем:
Из (19) вытекает, что максимально возможный темп прироста дохода равен мультипликатору.
б.Уровень потребления постоянен во времени
Тогда имеем следующее дифференциальное уравнение:
Из решения уравнения (21) следует, что:
Уравнение (22) описывает траекторию роста дохода при условии, что уровень потребления не изменяется во ремени. Тогда норма сбережения равна:
При
Темп прироста дохода , в этом случае равен:
Из (25) следует, что при То есть в предельном случае доля потребления стремиться к нулю и темп прироста дохода стремиться к значению мультипликатора.
Ниже представлен скприпт, который на основе численного решения уравнения (21), графически демонстрирует справедливость всех выше приведенных теоретических выводов.
using DifferentialEquations, Plots, PlotThemes
using StatsBase
#численное исследование модели (21)
function harrod2!(du, u, p, t)
σ, C0 = p
du[1] = σ * u[1] - σ*C0
end
u0 = [40.0]
tspan = (0.0, 4.5)
σ=1.25
C0=35.0
p = (σ,C0)
prob2 = ODEProblem(harrod2!, u0, tspan, p)
sol2 = solve(prob2, reltol=1e-8, abstol=1e-8)
# расчет I
I = zeros(length(sol2[:, :]))
for i in (1:length(sol2[:, :]))
I[i] = sol2[1, i] - C0
end
# расчет s
s = zeros(length(sol2[:, :]))
for i in (1:length(sol2[:, :]))
s[i] = I[i] / sol2[1, i]
end
#расчет dY/dt
dY = zeros(length(sol2[:, :]))
for i in (1:length(sol2[:, :]))
dY[i] = σ * sol2[1, i] - σ * C0
end
#РАСЧЕТ ro
ro = zeros(length(sol2[:, :]))
for i in (1:length(sol2[:, :]))
ro[i] = dY[i] / sol2[1, i]
end
plotly()
theme(:dao)
p1 = plot(sol2, linewidth=3, title="Модель Харрода (21) σ= $σ C0= $C0", label="Y(t)", lc=:red)
plot!(sol2.t, I, linewidth=3, label="I(t)", xlabel="Time (t)", ylabel="Y(t),I(t)", lc=:black)
p2 = plot(sol2.t, s, linewidth=3, title="Модель Харрода (21) σ= $σ C0= $C0", label="s(t)", ylabel="s(t),ro(t)",lc=:green)
plot!(sol2.t, ro, linewidth=3,label="ro(t)", xlabel="Time (t)")
plot(p1, p2, layout=(1, 2), wsize=(900, 350), legend=:outertopright)
Эта же задача решена на платформе Engee с помощью следующей динамической модели:
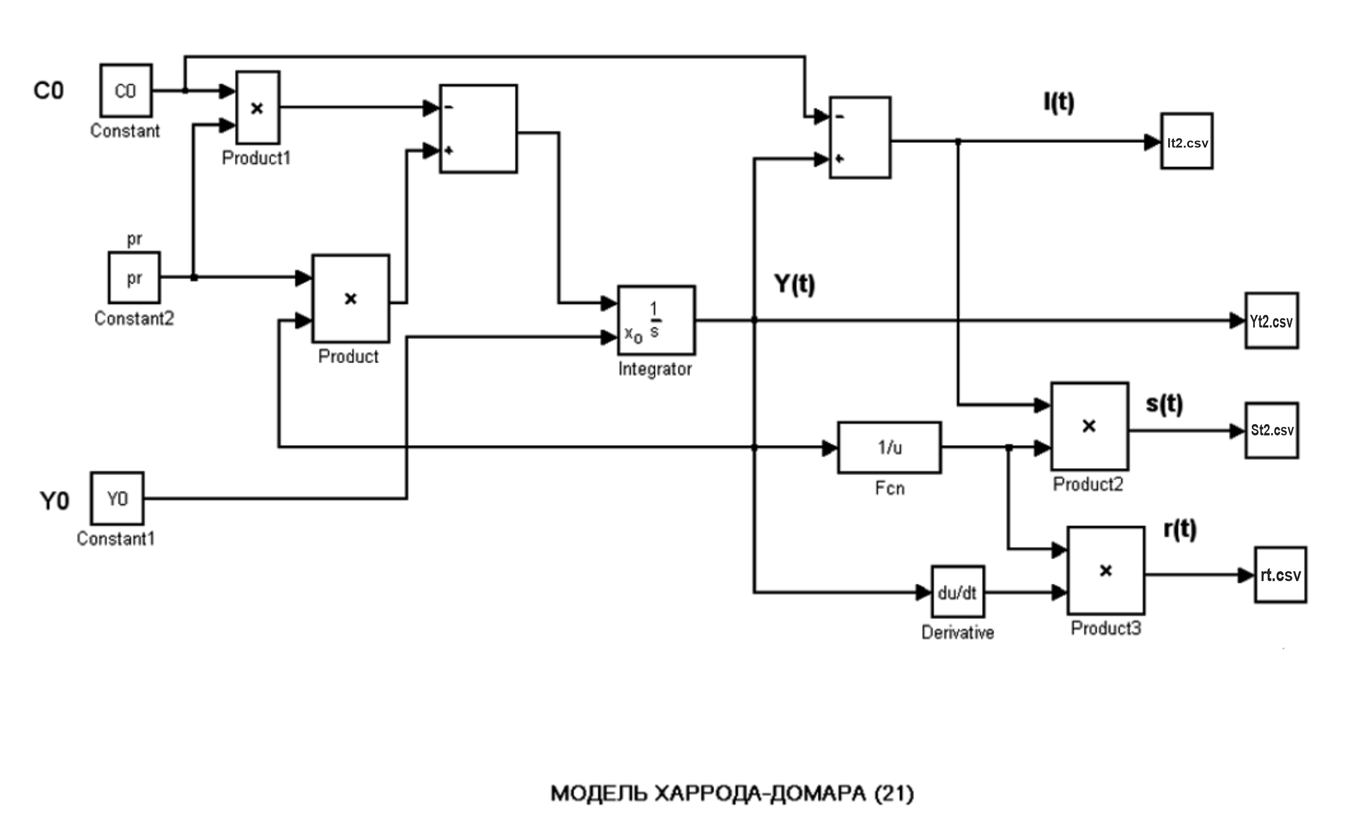
using RDatasets, Plots, PlotThemes
using CSV, DataFrames
#открытие модели
modelName = "Harrod21";
PID_model = modelName in [m.name for m in engee.get_all_models()] ? engee.open(modelName) : engee.load("/user/ModRost/$(modelName).engee");
engee.set_param!(modelName, "StopTime" => 4.5) # интервал моделирования
#Программа исследования непрерывной модели ХАРРОДА 21
# МУЛЬТИПЛИКАТОР-pr
pr = 1.25
#Начальная ЗНАЧЕНИЕ ДОХОДА - Y0
Y0 = 40.0
#постоянный уровень потребления
C0 = 35.0
#Выполнение модели
engee.run(modelName)
# ВЫДЫЧА РЕЗУЛЬТАТОВ МОДЕЛИРОВАНИЯ
#engee.get_results("Harrod01")
#modeling_variable = engee.get_results("Harrod01")
df_out1 = CSV.read("It2.csv", DataFrame)
df_out2 = CSV.read("Yt2.csv", DataFrame)
df_out3 = CSV.read("st2.csv", DataFrame)
df_out4 = CSV.read("rt2.csv", DataFrame)
#ГРАФИКИ
plotly()
theme(:ggplot2)
p1=plot(df_out1[!, "time"], df_out1[!, "1"],title="Модель Харрода (21) σ= $pr C0= $C0",label="It", lw=3)
plot!(df_out2[!, "time"], df_out2[!, "1"], label="Yt",xlabel="Time (t)",ylabel="Y(t),I(t)",lw=3)
p2=plot(df_out3[!,"time"],df_out3[!, "1"], label="st",lc=:green, lw=3,title="Модель Харрода (21) σ= $pr C0= $C0")
plot!(df_out4[2:end, "time"],df_out4[2:end, "1"], label="rot",xlabel="Time (t)",ylabel="s(t),ro(t)", lw=3,lc=:blue)
plot(p1, p2, layout=(1, 2), wsize=(900, 350),legend=:outertopright)
в. Потребление растет с постоянным темпом γ
То есть, имеем и тогда возможны следующие случаи
Случай 1 - потребление растет с темпом равным значению мультипликатора.
Тогда имеем следующее дифференциальное уравнение:
Решение этого уравнения имеет следующий вид:
Доход растет до тех пор, пока уровень инвестиций остается положительной величиной. То есть , чтобы определить интервал времени, в течении которого доход растет, необходимо решить уравнение:
Подставляя в левую часть (29) (27) и используя (28), получаем, что
при
Из (28) получаем при
Таким образом, при росте потребления с темпом равным значению мультипликатора доход растет в интервале времени от 0 до , достигая максимального значения ,а затем начинает падать и становиться равным 0 при .
using DifferentialEquations, Plots, PlotThemes
using StatsBase
#*Случай 1* γ = σ - потребление растет с темпом равным значению мультипликатора
#численное исследование модели (27)
function harrod3!(du, u, p, t)
σ, C0 = p
du[1] = σ * u[1] - σ * C0 * exp(σ*t)
end
u0 = [20.0]
tspan = (0.0, 2.3)
σ = 1.5
C0 = 6.0
p = (σ, C0)
Y0 = 20.0
@show t1 = (1.0 / σ) * (Y0 / C0 - 1)
@show t2 = (1.0 / σ) * (Y0 / C0);
prob3 = ODEProblem(harrod3!, u0, tspan, p)
sol3 = solve(prob3, reltol=1e-8, abstol=1e-8)
# расчет I
I = zeros(length(sol3[:, :]))
for i in (1:length(sol3[:, :]))
I[i] = sol3[1, i] - C0 * exp(σ * sol3.t[i])
end
plotly()
theme(:dao)
plot(sol3, linewidth=2, title="Случай 1 σ=γ= $σ C0= $C0 Y0= $Y0", label="Y(t)", lc=:green)
plot!(sol3.t, I, linewidth=2, label="I(t)", lc=:black)
plot!(vline!([1.556], lw=1, lc=:red,linestyle=:dash,label="t1=1.556"))
plot!(vline!([2.222], lw=1, lc=:red, linestyle=:dash, label="t2=2.222"))
plot!([1.556 2.222],[61.87 0.0], label=["Ymax=61.87" "Y=0.0"],
seriescolor=:red,
marker=:circle,
markersize=4,
markercolor=:red,
markerstrokecolor=:red,
wsize=(700, 450))
ylabel!("Y,I")
xlabel!("t")
Случай 2 -потребление растет с постоянным темпом, превышающим значение мультипликатора.
Тогда имеем следующее дифференциальное уравнение:
Решение этого уравнения имеет вид:
Из (32) и (33) вытекает, что темп прироста дохода в первоначальный момент времени равен:
где - норма сбережения в начальный момент времени. Таким образом, исходный темп прироста дохода положителен, но в (33) второе слагаемое отрицательно и поэтому с определенного момента времени доход начнет падать аналогично случаю 1.При этом точки и за счет
где - норма сбережения в начальный момент времени. Таким образом, исходный темп прироста дохода положителен, но в (33) второе слагаемое отрицательно и поэтому с определенного момента времени доход начнет падать аналогично случаю 1.При этом точки и за счет немного смещяются влево.
using DifferentialEquations, Plots, PlotThemes
using StatsBase
#*Случай 2* γ > σ - потребление растет с темпом равным значению мультипликатора
#численное исследование модели (32)
function harrod4!(du, u, p, t)
σ, γ, C0 = p
du[1] = σ * u[1] - σ * C0 * exp(γ*t)
end
u0 = [20.0]
tspan = (0.0, 2.3)
σ = 1.5
γ =1.6
C0 = 6.0
p = (σ, γ, C0)
Y0 = 20.0
prob4 = ODEProblem(harrod4!, u0, tspan, p)
sol4 = solve(prob4, reltol=1e-8, abstol=1e-8)
# расчет I
I = zeros(length(sol4[:, :]))
for i in (1:length(sol4[:, :]))
I[i] = sol4[1, i] - C0 * exp(γ*sol4.t[i])
end
plotly()
theme(:dao)
plot(sol4, linewidth=2, title="Случай 2 σ= $σ γ=$γ C0= $C0 Y0= $Y0", label="Y(t)", lc=:green)
plot!(sol4.t, I, linewidth=2, label="I(t)", lc=:black )
plot!(vline!([1.36], lw=1, lc=:red, linestyle=:dash, label="t1=1.36"))
plot!(vline!([2.0], lw=1, lc=:red, linestyle=:dash, label="t2=2.0"))
plot!([1.36 2.0], [52.98 0.0], label=["Ymax=52.98" "Y=0.0"],
seriescolor=:red,
marker=:circle,
markersize=4,
markercolor=:red,
markerstrokecolor=:red,
wsize=(700, 450))
ylabel!("Y,I")
xlabel!("t")
Случай 3 и - темп прироста потребления меньше значения мультипликатора и меньше первоначального темпа прироста дохода
Рассмотрим (33) второе слагаемое в силу условия положительно, потребуем чтобы и первое слагаемое тоже было положительно, То есть имеем:
Следовательно, в этом случае доход постоянно растет во времени. При величина , 1, то есть в пределе потребление стремиться к нулю.
using DifferentialEquations, Plots, PlotThemes
using StatsBase
#=*Случай 3* γ < σ и γ<s0 - темп прироста потребления меньше значения мультипликатора
и меньше первоначального темпа прироста дохода
численное исследование модели (32)=#
function harrod5!(du, u, p, t)
σ, γ, C0 = p
du[1] = σ * u[1] - σ * C0 * exp(γ * t)
end
u0 = [20.0]
tspan = (0.0, 8.0)
σ = 1.5
γ = 0.6
C0 = 10.0
p = (σ, γ, C0)
Y0 = 20.0
s0 =10.0/20
b = σ * s0
prob5 = ODEProblem(harrod5!, u0, tspan, p)
sol5 = solve(prob5, reltol=1e-8, abstol=1e-8)
# расчет I
I = zeros(length(sol5[:, :]))
for i in (1:length(sol5[:, :]))
I[i] = sol5[1, i] - C0 * exp(γ * sol5.t[i])
end
# расчет s
s = zeros(length(sol5[:, :]))
for i in (1:length(sol5[:, :]))
s[i] = I[i] / sol5[1, i]
end
#расчет dY/dt
dY = zeros(length(sol5[:, :]))
for i in (1:length(sol5[:, :]))
dY[i] = σ * sol5[1, i] - σ * C0 * exp(γ * sol5.t[i])
end
#РАСЧЕТ ro
ro = zeros(length(sol5[:, :]))
for i in (1:length(sol5[:, :]))
ro[i] = dY[i] / sol5[1, i]
end
plotly()
theme(:dao)
p1 = plot(sol5, linewidth=3, label="Y(t)",ylabel="Y(t)", lc=:black)
p2 = plot(sol5.t, s, linewidth=3, ylabel="s(t),ro(t)",label="s(t)", lc=:green)
plot!(sol5.t, ro, linewidth=3, label="ro(t)", xlabel="Time (t)", lc=:blue)
plot(p1, p2, layout=(1, 2), wsize=(1000, 350), legend=:outertopright)
title!("Случай 3 σ= $σ γ=$γ C0= $C0 Y0= $Y0 σ*s0 =$b")
Случай 4 и - темп прироста потребления меньше значения мультипликатора и равен первоначальному темпу прироста дохода. Имеем дифференциальное уравнение:
Решение этого уравнения имеет следующий вид:
тогда имеем:
Таким образом, норма сбережения в этом случае будет постоянной, темп прироста дохода будет равен произведению этой нормы на технологический мультипликатор.
using DifferentialEquations, Plots, PlotThemes
using StatsBase
#=Случай 4 γ < σ и γ=s0*σ -темп прироста потребления меньше значения мультипликатора
и равен первоначальному темпу прироста дохода.
численное исследование модели (35)=#
function harrod6!(du, u, p, t)
σ, s0, C0 = p
du[1] = σ * u[1] - σ * C0 * exp(σ*s0*t)
end
u0 = [20.0]
tspan = (0.0, 8.0)
σ = 1.5
C0 = 10.0
Y0 = 20.0
s0 = (Y0-C0)/Y0
γ =σ * s0
p = (σ, s0, C0)
prob6 = ODEProblem(harrod6!, u0, tspan, p)
sol6 = solve(prob6, reltol=1e-8, abstol=1e-8)
# расчет I
I = zeros(length(sol6[:, :]))
for i in (1:length(sol6[:, :]))
I[i] = sol6[1, i] - C0 * exp(σ*s0*sol6.t[i])
end
# расчет s
s = zeros(length(sol6[:, :]))
for i in (1:length(sol6[:, :]))
s[i] = I[i] / sol6[1, i]
end
#расчет dY/dt
dY = zeros(length(sol6[:, :]))
for i in (1:length(sol6[:, :]))
dY[i] = σ * sol6[1, i] - σ * C0 * exp(σ*s0*sol6.t[i])
end
#РАСЧЕТ ro
ro = zeros(length(sol6[:, :]))
for i in (1:length(sol6[:, :]))
ro[i] = dY[i] / sol6[1, i]
end
plotly()
theme(:dao)
p1 = plot(sol6, linewidth=3, label="Y(t)", ylabel="Y(t)", lc=:black)
p2 = plot(sol6.t, s, linewidth=3, ylabel="s(t),ro(t)", label="s(t)", lc=:green)
plot!(sol6.t, ro, linewidth=3, label="ro(t)", xlabel="t", lc=:blue)
plot(p1, p2, layout=(1, 2), wsize=(1000, 350), legend=:outertopright)
title!("Случай4 σ= $σ γ=$γ C0= $C0 Y0= $Y0 σ*s0 =$γ")
Случай 5 s0σ < γ < σ - темп прироста потребления меньше значения мультипликатора,но больше первоначального темпа прироста дохода.В этом случае доход сначало растет на интервале времени, величина которого определяется значением γ (этот интервал тем меньше, чем больше γ превосходит s0σ),а затем резко падает вниз. При этом s и ro к концу этого интервала времени обращаются в ноль, то есть система разрушается.
using DifferentialEquations, Plots, PlotThemes
using StatsBase
#=Случай 5 s0*σ < γ < σ -темп прироста потребления меньше значения мультипликатора,но больше первоначального темпа прироста дохода
численное исследование модели (32)=#
function harrod7!(du, u, p, t)
σ, γ, C0 = p
du[1] = σ * u[1] - σ * C0 * exp(γ*t)
end
u0 = [20.0]
tspan = (0.0, 3.15)
σ = 1.5
C0 = 10.0
Y0 = 20.0
s0 = (Y0 - C0)/Y0
γ = 0.8
b = σ*s0
p = (σ, γ, C0)
prob7 = ODEProblem(harrod7!, u0, tspan, p)
sol7 = solve(prob7, reltol=1e-8, abstol=1e-8)
# расчет I
I = zeros(length(sol7[:, :]))
for i in (1:length(sol7[:, :]))
I[i] = sol7[1, i] - C0 * exp(γ*sol7.t[i])
end
# расчет s
s = zeros(length(sol7[:, :]))
for i in (1:length(sol7[:, :]))
s[i] = I[i] / sol7[1, i]
end
#расчет dY/dt
dY = zeros(length(sol7[:, :]))
for i in (1:length(sol7[:, :]))
dY[i] = σ * sol7[1, i] - σ * C0 * exp(γ*sol7.t[i])
end
#РАСЧЕТ ro
ro = zeros(length(sol7[:, :]))
for i in (1:length(sol7[:, :]))
ro[i] = dY[i] / sol7[1, i]
end
plotly()
theme(:dao)
p1 = plot(sol7,linewidth=3, label="Y(t)", ylabel="Y(t)", lc=:black)
plot!(sol7.t, I,linewidth=3, label="Y(t)", ylabel="Y(t)", lc=:black)
p2 = plot(sol7.t, s, linewidth=3, ylabel="s(t),ro(t)", label="s(t)", lc=:green)
plot!(sol7.t, ro, linewidth=3, label="ro(t)", xlabel="t", lc=:blue)
plot(p1, p2, layout=(1, 2), wsize=(1000, 350), legend=:outertopright)
title!("Cлучай 5 σ= $σ γ=$γ C0= $C0 Y0= $Y0 σ*s0 =$b")
Проанализируем модель Харрода (27) с помощью динамической модели Engee:
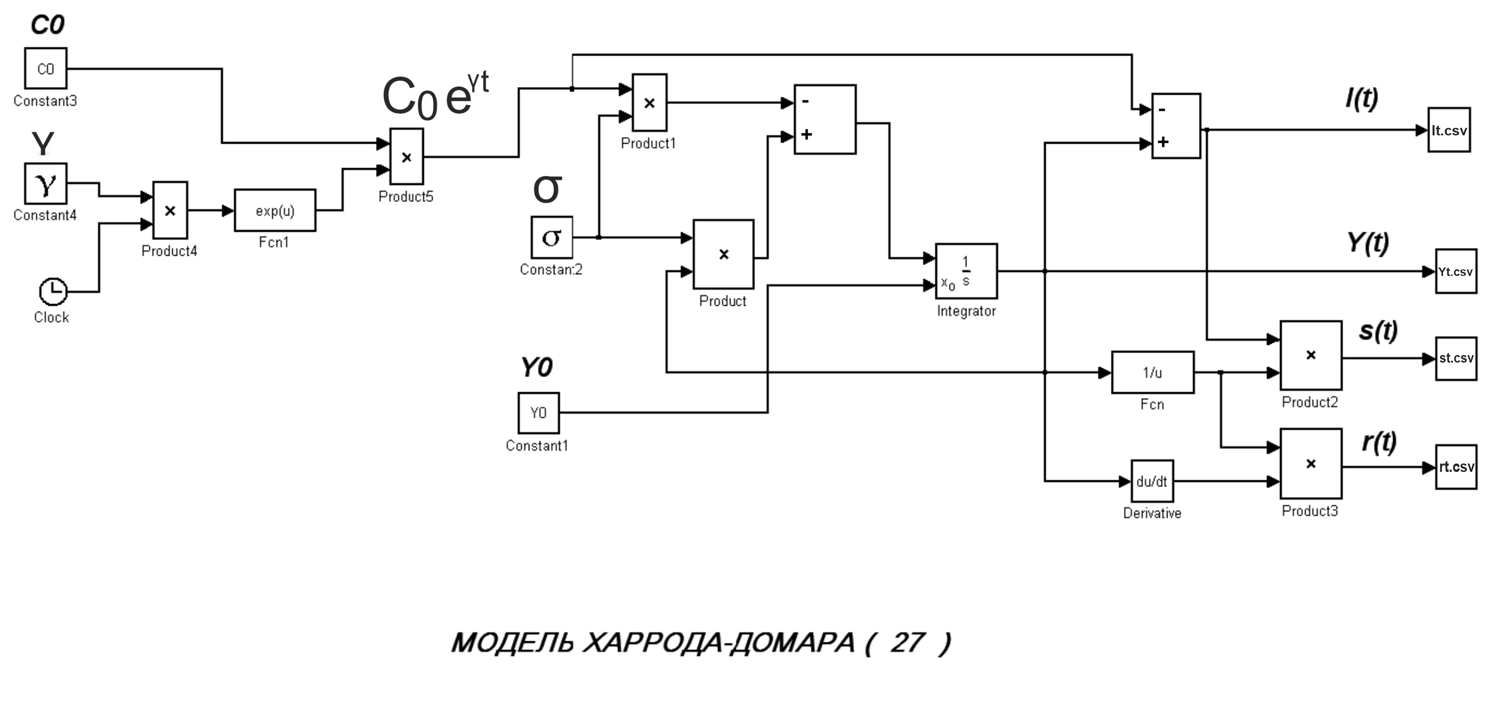
using RDatasets, Plots, PlotThemes
using CSV, DataFrames
#Харрод модель (27)
#открытие модели
modelName = "Harrod27";
PID_model = modelName in [m.name for m in engee.get_all_models()] ? engee.open(modelName) :
engee.load("/user/ModRost/$(modelName).engee");
global σ = 1.5
global Y0 = 20.0
global γ1 = σ #Случай 1* γ = σ
global γ2 = 1.6 #Случай 2 γ > σ
global γ3 = 0.6 #Случай 3* γ < σ и γ<s0
global γ4=0.0 # Случай 4 γ < σ и γ=s0*σ
global γ5 = 0.8 #Случай 5 s0*σ < γ < σ
global γm = [γ1, γ2, γ3,γ4,γ5]
for i in (1:5)
global γ=γm[i]
if (γ == γ1)
global C0=6.0
engee.set_param!(modelName, "StopTime" => 2.3)
engee.run(modelName)
df_It = CSV.read("It.csv", DataFrame)
df_Yt = CSV.read("Yt.csv", DataFrame)
global p1=plot(df_It[!, "time"], df_It[!, "1"], label="I(t)", lw=3)
plot!(df_Yt[!, "time"], df_Yt[!,"1"], label="Y(t)", lw=3,title="Случай1 σ=γ1= $σ C0 = $C0 Y0= $Y0")
elseif (γ == γ2)
global C0=6.0
engee.set_param!(modelName, "StopTime" => 2.3)
engee.run(modelName)
df_It = CSV.read("It.csv", DataFrame)
df_Yt = CSV.read("Yt.csv", DataFrame)
global p2 = plot(df_It[!, "time"], df_It[!, "1"], label="I(t)", lw=3)
plot!(df_Yt[!, "time"], df_Yt[!, "1"], label="Y(t)", lw=3,title="Случай2 γ2= $γ2 C0 = $C0 Y0= $Y0")
elseif (γ == γ3)
global CO=10.0
engee.set_param!(modelName, "StopTime" => 8.0)
engee.run(modelName)
df_st = CSV.read("st.csv", DataFrame)
df_rt = CSV.read("rt.csv", DataFrame)
global p3 = plot(df_st[!, "time"], df_st[!, "1"], label="s(t)", lw=3)
plot!(df_rt[2:end,"time"],df_rt[2:end,"1"], label="ro(t)",lw=3,title="Случай3 γ3= $γ3 C0=$C0 Y0=$Y0")
elseif (γ == γ4)
global C0 =10.0
s0 = (Y0 - C0)/Y0
global γ = σ * s0
engee.set_param!(modelName, "StopTime" => 6.0)
engee.run(modelName)
df_st = CSV.read("st.csv", DataFrame)
df_rt = CSV.read("rt.csv", DataFrame)
global p4 = plot(df_st[!, "time"], df_st[!, "1"], label="s(t)", lw=3)
plot!(df_rt[2:end,"time"],df_rt[2:end,"1"], label="ro(t)",lw=3,title="Случай2 γ4= $γ C0=$C0 Y0=$Y0")
else
engee.set_param!(modelName, "StopTime" => 3.5)
engee.run(modelName)
df_It = CSV.read("It.csv", DataFrame)
df_Yt = CSV.read("Yt.csv", DataFrame)
global p5 = plot(df_It[!, "time"], df_It[!, "1"], label="I(t)", lw=3)
plot!(df_Yt[!, "time"],df_Yt[!, "1"], label="Y(t)", lw=3,title="Случай5 γ5= $γ5 C0 = $C0 Y0= $Y0")
end
end
plot(p1)
plot(p2)
plot(p3)
plot(p4)
plot(p5)
Решим для примера две задачи, используя модель Харрода-Домара:
-
Найти максимально возможный темп прироста дохода для экономики, в которой σ =0.25 и определить,через, сколько времени в этой экономике доход увеличиться вдвое.
-
Имеем экономику, в которой отсутствует потребление, и акселератор a зависит от времени следующим образом: , где − значение акселератора в начальный момент времени,. Определить предел роста дохода и построить его траекторию во времени.
Задача 1
Максммальный темп прироста дохода,согласно модели,будет в экономике, где s=1.0 , следовательно, потребление тоже равно нулю, а темп прироста дохода будет максимальным и равным мультипликатору σ =0.25. Ниже приведен скрипт,который на основе использования модели с максимальным темпом прироста дохода определяет диапозон времени [0.0,2.775], за который доход увелечится вдвое.
using DifferentialEquations, Plots, PlotThemes
using StatsBase
function harrod!(du, u, p, t)
σ, s = p
du[1] = σ * s * u[1]
end
u0 = [20.0]
Y0=20.0
σ=0.25
s = 1.0
p = (σ, s)
Tk = 0.005:0.005:10.0
#tk = Tk[6]
for i in (1:length(Tk))
global tk = Tk[i]
tspan = (0.0, tk)
prob = ODEProblem(harrod!, u0, tspan, p)
global sol = solve(prob, reltol=1e-8, abstol=1e-8)
a = sol.u[end] / 20.0
if (a >= [2.0])
break
end
end
@show tspan = (0.0, tk);
@show sol.u[end];
plot(sol, linewidth=3,label="Y(t)",lc=:blue)
title!("σ=ro=$σ s=$s Y0= $Y0 tk=$tk")
ylabel!("Y")
xlabel!("t")
Задача 2
Акселератор . Используем модель без потребления с переменным мультипликатором σ(t),s=1.0 , a(0) = 0.4 и k=2.5. Ниже представлен скрипт, позволяющий определять предел роста дохода в такой экономике.
using DifferentialEquations, Plots, PlotThemes
using StatsBase
function harrod22!(du, u, p, t)
σ0, s, k = p
du[1] = σ0 *exp(-k*t)*s* u[1]
end
u0 = [20.0]
Y0 = 20.0
a0 =0.4
σ0 = 1/a0
s = 1.0
k=2.5
p = (σ0,s,k)
tspan = (0.0, 4.0)
prob = ODEProblem(harrod22!, u0, tspan, p)
sol = solve(prob, reltol=1e-8, abstol=1e-8)
@show round.(sol.u[end], sigdigits=4);
#Yinf = round(sol.u[end],sigdigits=2)
Yinf = sol[:, end]
Yinf = round.(Yinf, sigdigits=4)
plotly()
theme(:dao)
plot(sol, linewidth=2, label="Y(t)", lc=:blue)
plot!(hline!([Yinf], lw=4, lc=:red, linestyle=:dash, label="Yinf= $Yinf"))
title!("σ0=$σ0 a0=$a0 s=$s Y0= $Y0 k=$k")
ylabel!("Y")
xlabel!("t")
Выводы
Таким образом, согласно модели Харрода-Домара наиболее разумным вариантом экономического развития является такое развитие, при котором потребление и накопление растут с постоянным темпом, причем темп прироста дохода
также постоянен и равен σ*s0 (случай 4).
Из модели Харрода следует, что постоянного сбалансированного роста можно достичь двумя путями.
-
В начальный момент выбирается норма сбережения s0 и тогда ищется оптимальный темп роста
потребления γ=σ*s0. -
Выбирается желаемый темп роста потребления γ и тогда ищется норма накопления s0 = γ/σ, обеспечивающая этот темп.
При сбалансированном равновесном росте темпы прироста предложения (дохода), потребления и инвестиций совпадают и равны σ*s.
Попытки прогнозировать экономический рост на основе модели Харрода-Домара оказались неудачными. Исследователи пришли к выводу, что модель не объясняет основных детерминант роста.
ИССЛЕДОВАНИЕ МОДЕЛИ Р.СОЛОУ- Т.СВАНА
1. Краткие теоретические сведения
Модель построена на следующих постулатах :
-
Рассматривается однопродуктовая закрытая экономика без государства;
-
Абстрагируются:
-
от индивидуальных предпочтений домашних хозяйств;
-
от наличия разных производящих секторов в экономике;
-
от существования в экономике взаимозависимостей.
-
В экономике имеется большое число одинаковых репрезентативных домохозяйств, т.е. спрос и предложение труда могут быть представлены на примере единственного домохозяйства. Домохозяйства владеют всем наличным трудом и капиталом и полностью их поставляют на рынок. При этом имеет место полная занятость.
-
В экономике имеется очень большое число одинаковых репрезентативных фирм, т.е. все фирмы характеризуются одной и той же неоклассической ПФ:
Где
– доход (конечный произведенный продукт) в период
- капитал в экономике в период
-труд в экономике в период
– технология в экономике впериод (она находится в свободном доступе, т.е является неконкурентным и не исключаемым благом)
- Свойства неоклассической ПФ
ПФ является дважды дифференцируемой по K и L и удовлетворяет неравенствам:
ПФ обладает постоянной отдачей от масштаба, т.е. является линейно однородной:
- Эндогенные факторы:
-
– доход (конечный продукт) в период ;
-
- потребление в период ;
-
- сбережение в период ;
-
- инвестиции в период ;
-
- капитал в период ;
-
- прирост капитала в период ;
-
- капитал в период ;
-
- население в период ;
-
- население в период .
- Экзогенные факторы:
-
s =const -норма сбережения;
-
норма выбытия капитала;
-
темп роста населения;
-
-капитал в период ;
-
– население в период ;
-
- неоклассическая ПФ.
1.1 Базовый объемный вариант модели Солоу-Свана в дискретном времени (основные уравнения и логика движения экономики).
- Объем выпуска (национального дохода) в любой период дискретного времени t определяется уравнением:
- Доход должен быть равен сумме сбережений и потребления (уравнение Кейнса):
– потребление в период ; - сбережения в период
Сбережения формируются домашними хозяйствами в экономике как некоторая постоянная доля дохода (норма сбережения ), тогда имеем:
Потребление из (2) и (3) будет тогда равно:
- Считается, что все сбережения идут на инвестиции в капитал:
- Инвестиции в период тратятся на восстановление капитала, который износился за этот период (капитал теряет свою стоимость с темпом , т. е. за период t будет потеряно капитала) и на приобретение нового капитала на период .
Следовательно, имеем:
Из (6) и (5) получаем:
Подставляя (8) в (7), получаем основное уравнение движения капитала в модели Солоу-Свана:
- Труд (население) в модели считается растущим cпостоянным темпом :
- Логика движения экономики по Солоу в дискретном времени представлена на рис.1
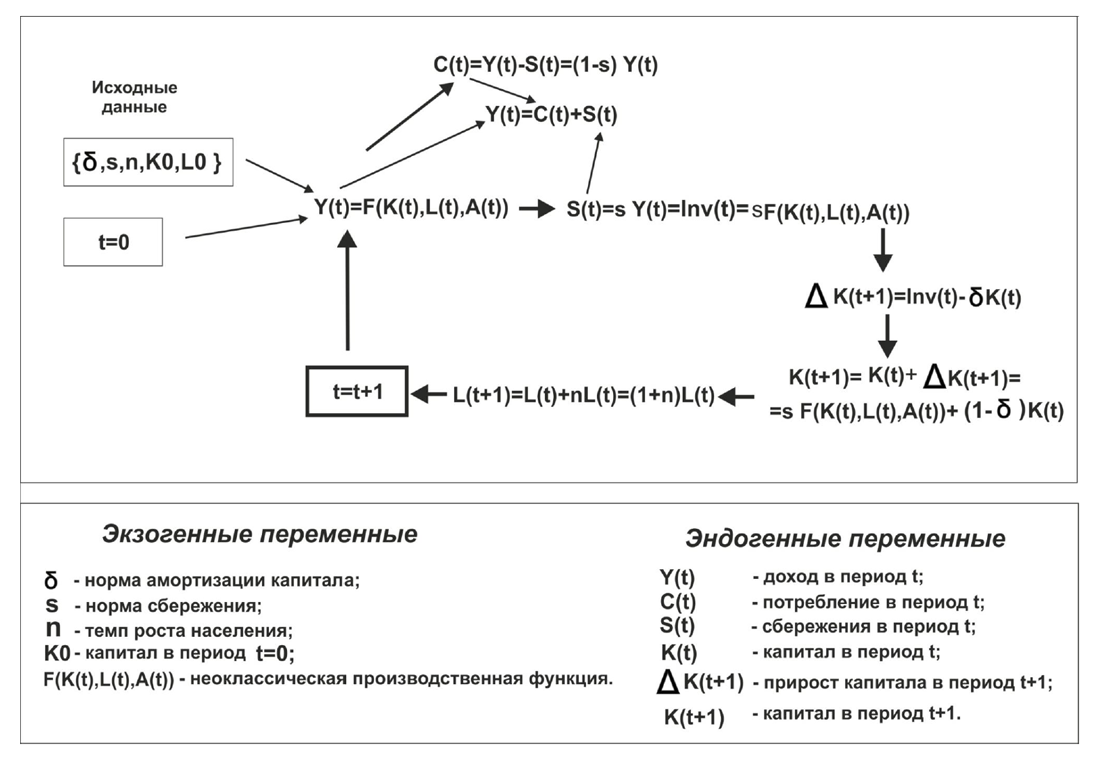
using Plots, PlotThemes
using StatsBase
#МОДЕЛИВАНИЕ ДИНАМИКИ ЭКОНОМИКИ ПО ОБЪЕМНОЙ ДИСКРЕТНОЙ МОДЕЛИ СОЛОУ
#ЗАДАНИЕ ИСХОДНЫХ ДАННЫХ
#горизонт прогноза
T=100;
#норма амортизации капитала
δ = 0.25;
#норма сбережения
s=0.6;
#темп роста труда
n=0.02;
#эластичность выпуска по капиталу
α = 0.5;
# производственная функция F= K(t)^α *L(t)^(1-α)
#начальное значение
Y = zeros(T + 1)
C = zeros(T + 1)
Inv = zeros(T + 1)
K = zeros(T + 1)
L = zeros(T + 1)
t=1;
K[t]=50.0;
L[t]=100.0
#Расчет эндогенных переменных модели для t
#выпуск
Y[t]=K[t]^α*L[t]^(1-α);
#потребление
C[t]=(1-s)*Y[t];
#инвестиции
Inv[t]=s*Y[t];
#рост капитала
K[t+1]=s*Y[t]+(1-δ)*K[t]
#рост населения
L[t+1]=(1+n)*L[t]
for t in (2:T)
Y[t]=K[t]^α*L[t]^(1-α);
C[t]=(1-s)*Y[t];
Inv[t]=s*Y[t];
K[t+1]=s*Y[t]+(1-δ)*K[t]
L[t+1]=(1+n)*L[t]
end
t = 1:T
plotly()
theme(:dao)
plot(t, Y[1:T], title="Y , C , Inv ", ylabel="Y,C,Inv", xlabel="t", label="Объем производства", lw=2)
plot!(t, C[1:T], label="Потребление", lw=3)
plot!(t, Inv[1:T], label="Инвестиции", lw=2, wsize=(700, 400))
1.2 Базовый удельный вариант модели Солоу-Свана в дискретном времени (основные уравнения и логика движения экономики).
Рассмотрим удельный вариант модели, в котором рассматриваются соответствующие экономические величины приведенные к одному работнику.
- Разделим обе части уравнения (1) на получим:
где
-доход на душу населения т.е. производительность труда;
- капиталовооруженность ;
-технологический прогресс отсутствует.
- Аналогично из (3) (4) и (5) имеем:
где
-сбережение на душу населения;
-потребление на душу населения
-инвестиции на душу населения
- Из уравнений (5) (6) имеем:
Так как получаем:
Найдем ,следовательно:
Из (16)и (17) имеем :
Разностный аналог уравнения (18) имеет вид:
Тогда имеем:
- Логика движения экономики по Солоу в удельном варианте и дискретном времени представлена на рис.2
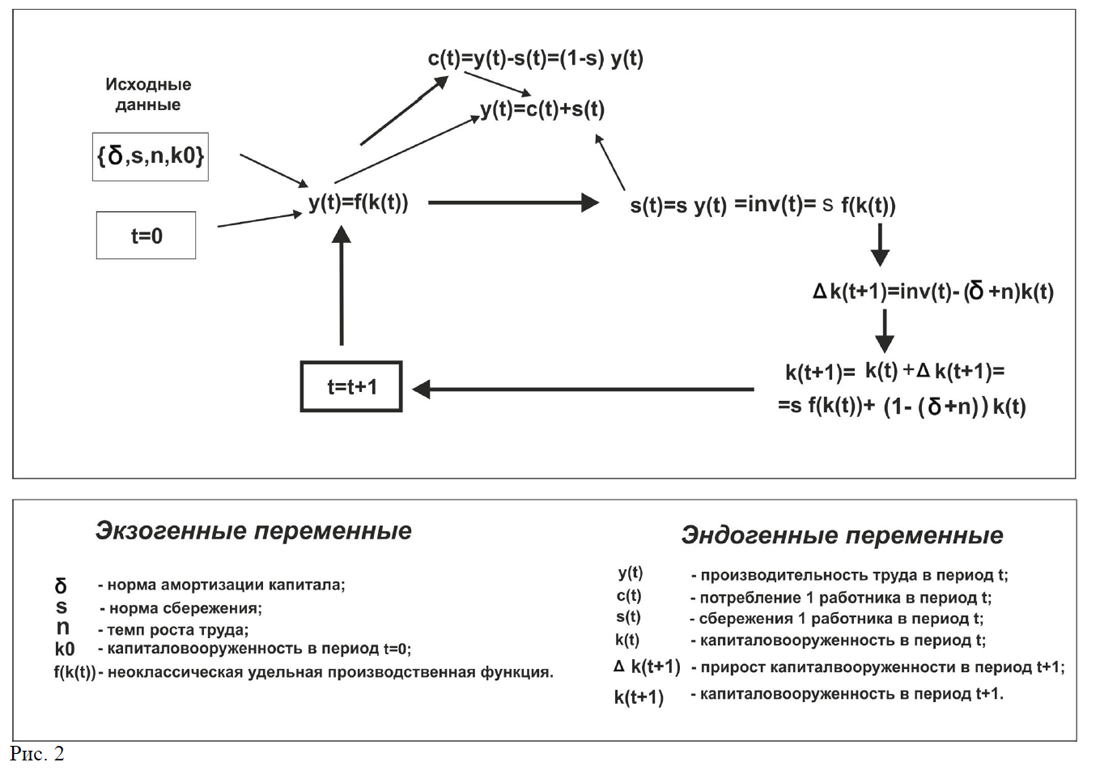
1.3 Анализ модели Солоу-Свана
1. Стационарное состояние экономики.
ПФ , определяющая объем выпуска на душу населения в любой момент времени , является монотонно возрастающей функцией от капиталовооруженности , т. е имеем:
Следовательно, при . То есть
Динамика функции зависит от соотношения динамик капитала и населения, если капитал растет быстрее населения, то возрастает при обратном соотношении падает. Можно показать, что существует такое состояние, к которому стремится экономика, где ,то есть . В этом состоянии темп роста выпуска, потребления и капитала равны темпу роста населения. Такое состояние экономики называется стационарным, точка стационарной. Найдем стационарную точку из условия:
Стационарную точку можно найти и графически рис 3
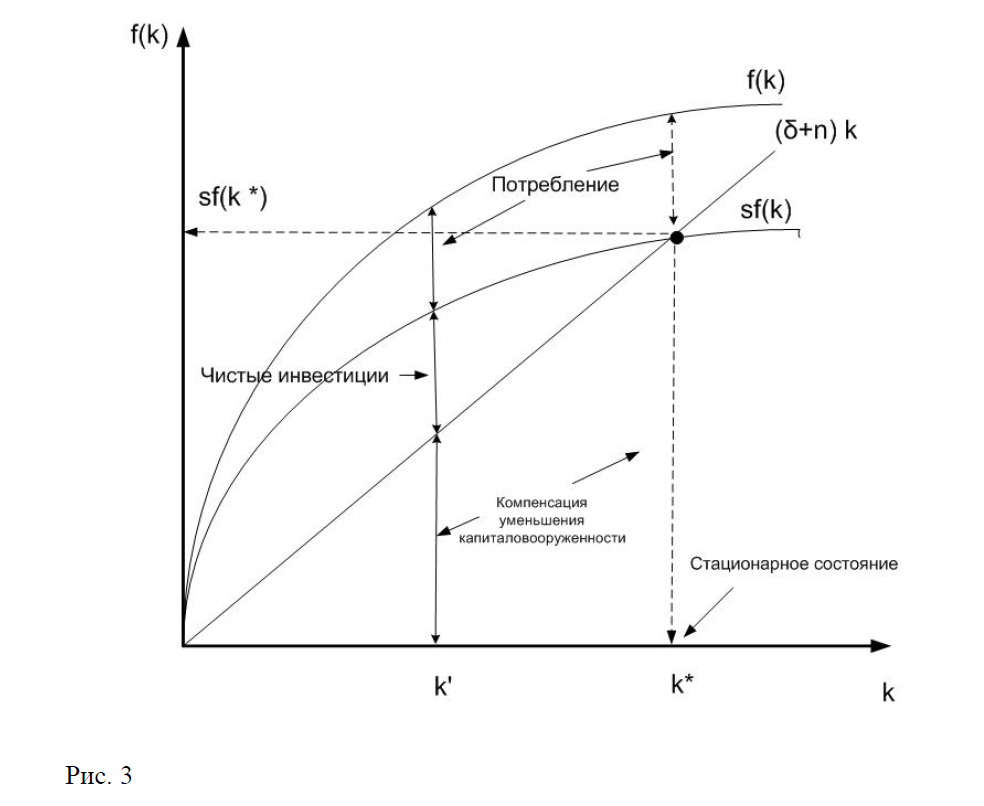
На рис. 3 представлены: функция - объем выпуска на душу населения, функция - объем сбережений на душу населения и функция , характеризующая объем инвестиций на душу населения необходимых для обеспечения постоянства капиталовооруженности.Точка пересечения и представляет собой стационарную точку .В интервале
имеем .т.е.инвестиций в экономике больше, чем это необходимо для обеспечения постоянства капиталовооруженности. Рассмотрим экономику в точке
в этой точке величина представляет собой чистые инвестиции на душу населения, которые увеличивают капиталовооруженность, а величина характеризует объем потребления на душу населения. В стационарной точке , т.е чистые инвестиции равны нулю, а объем потребления равен
Докажем существование стационарной точки. Рассмотрим точку в окрестности начала координат где положительная бесконечно малая величина, тогда и из (23) имеем , следовательно:
Рассмотрим точку в окрестности конца координат тогда из (22) и из (23) имеем и ,следовательно:
Таким образом, так как функция (k(t))$ \text{в} \text{интервале} \text{монотонно} \text{возрастающая}, \text{гладкая}, \text{непрерывная} \text{и} \text{удовлетворяющая} \text{условиям} (21, 22) \text{и} линейно растущая функция, то в этом интервале обязательно выполняется условие:
Это эквивалентно существованию стационарной точки.
2. Золотое правило накопления капитала
Из (24) видно, что стационарное состояние экономики зависит от нормы сбережения , а следовательно, от нормы сбережения зависит и потребление на душу населения в стационарной точке. Как изменяется стационарное потребление на душу населения при изменении нормы сбережения и какова норма сбережения, которая максимизирует стационарное потребление. Из (14) имеем:
Из (25) имеем:
Тогда условие максимума потребления имеет вид:
Стационарная капиталовооруженность получаемая из уравнения (28) называется капиталовооруженностью, соответствующей золотому правилу и обозначается - :
Уравнение (29) определяющее стационарную капиталовооруженность максимизирующую стационарное потребление называется золотым правилом накопления капитала. Из (25) и (29) имеем норму сбережения, обеспечивающую макси-
мальное потребление на душу население :
Величина максимального стационарного потребления определяетсяиз уравнения:
Проиллюстрируем золотое правило накопления капитала графически (рис.4).Капиталовооруженность в стационарном состоянии экономики соответствует золотому правилу, так как определяется нормой сбережения , которая задает максимальное стационарное потребление на душу населения . Уменьшение нормы сбережения и ее увеличение уменьшают стационарное потребление на душу населения, т.е. и . При этом угол наклона касательной к функции выпуска в точке равен ,что эквивалентно условию (29).
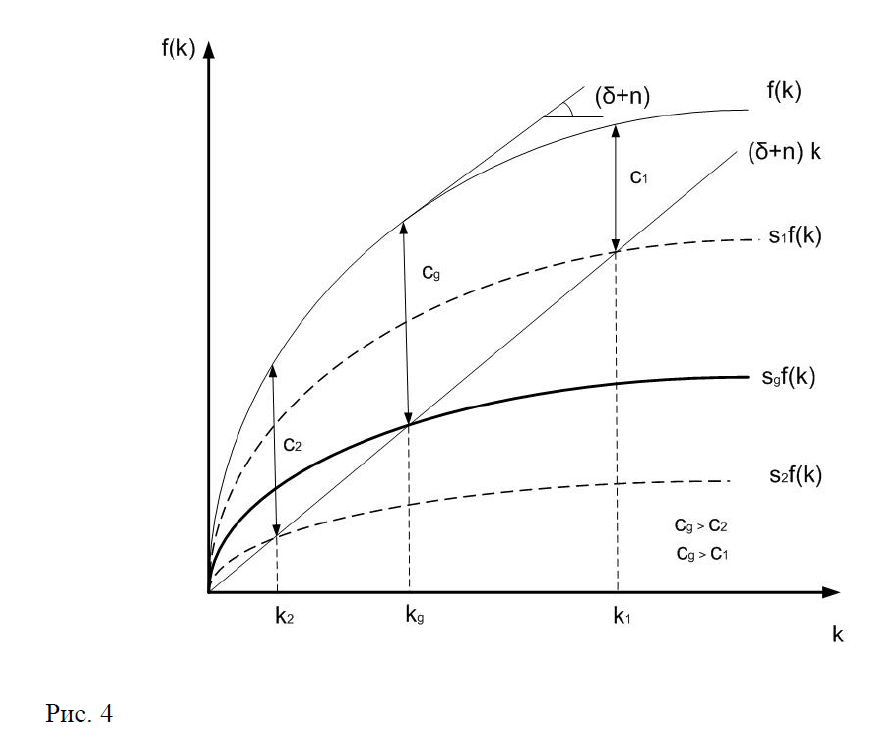
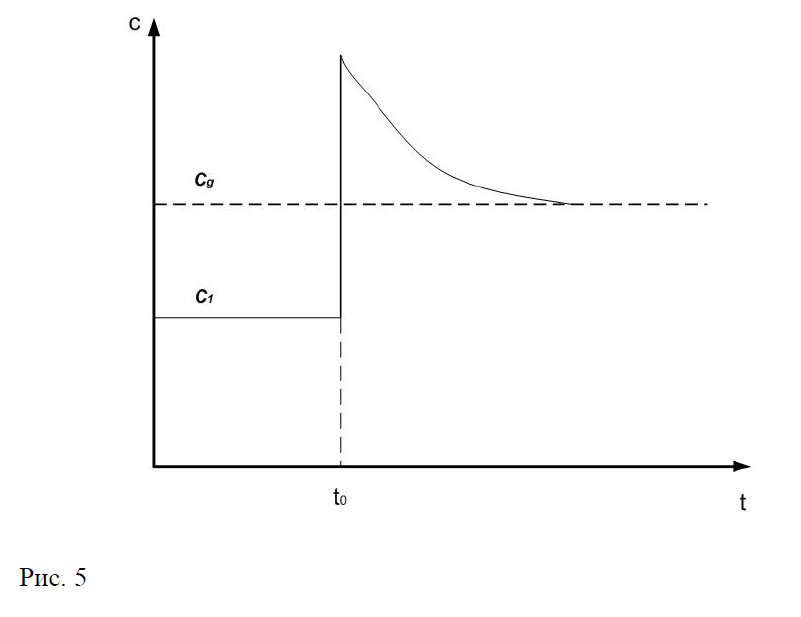
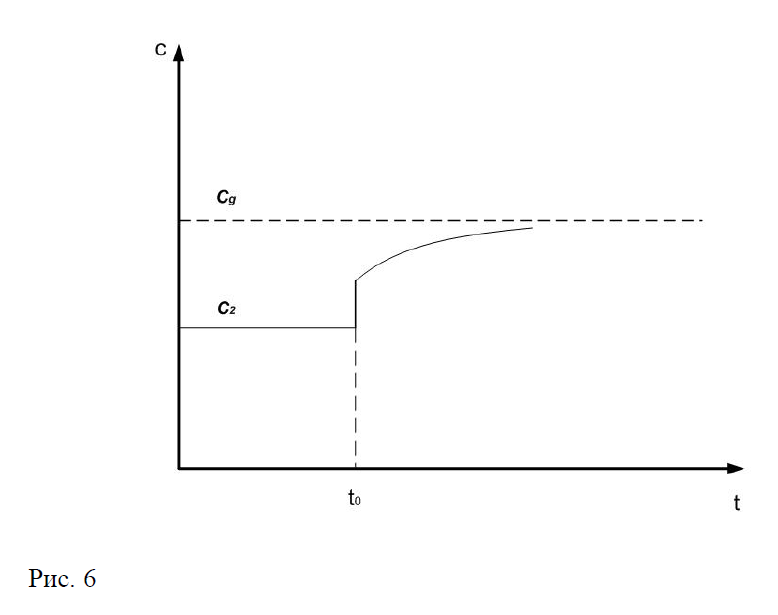
При переходе экономики из стационарного состояния с нормой сбережения с к стационарному состоянию с нормой () увеличивается соответственно стационарное потребление на душу населения с уровня до уровня . Но процесс этот не одномоментный, а имеет следующий вид (рис. 5). То есть экономика имеющая ному сбережения больше чем сберегает слишком много и распределение ресурсов в этом случае является динамически неэффективным.Если норма сбережения в экономике и меньше чем , то увеличив ее до уровня мы увеличиваем стационарную капиталовооруженность с уровня до уровня , но в переходный период потребление на душу населения остается ниже (рис.6). Однозначно определить эффективно распределяются ресурсы или нет нельзя, потому что нельзя оценить, что важнее текущее состояние или будущее.
3. Экономический рост: долгосрочная динамика и переходный период.
В стационарном состоянии капиталовооруженность постоянна, следовательно, постоянна и производительность труда. Таким образом, долгосрочный рост выпуска не зависит от экзогенных параметров нормы сбережения и нормы
амортизации, а зависит только от темпов роста населения. Однако эти экзогенные параметры влияют на производительность труда в переходный период при движении экономики к стационарному состоянию.
Рассмотрим, чем определяется темп роста капиталовооруженности на равновесной траектории. Поделим обе части уравнения (18) на kполучим уравнение динамики темпа роста капиталовооруженности:
Изобразим динамику экономики в модели Солоу, описываемую уравнением (32) графически (рис. 7).
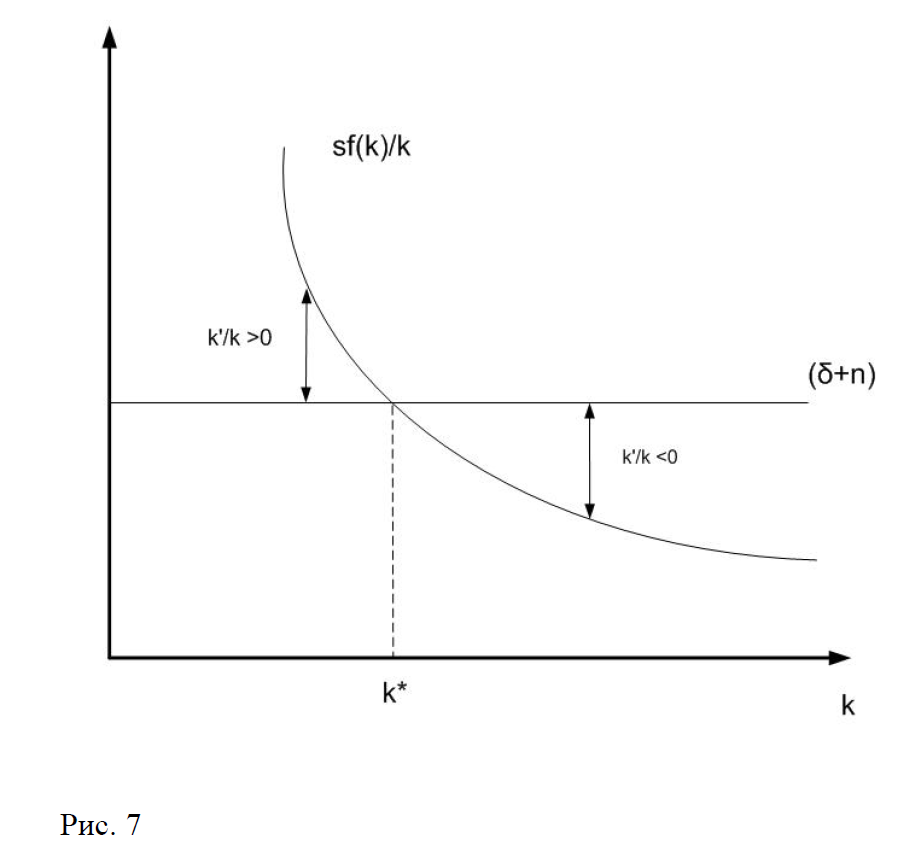
Как видно является убывающей функцией . Расстояние по вертикали между и является темпом роста капиталовооруженности в точке пересечения (в стационарной точке ) . Слева от стационарной точки , а справа . Динамика темпа роста роизводительности труда аналогична динамике темпа роста капиталовооруженности. Продифференцируем уравнение (12) имеем:
Разделим обе части уравнения (33) на получаем:
Анализируя стационарное состояние можно сделать следующее заключение, что стационарное состояние зависит от нормы сбережения, нормы амортизации и темпа роста населения.
а. Изменение нормы сбережения.
При повышении нормы сбережения с до кривая смещается вверх и стационарная точка перемещается из в т.е. стационарная капиталовооруженность возрастает (рис.8). Как видно из рис.8 при росте нормы сбережения темп роста капиталовооруженности скачком возрастает и становится выше темпа роста населения, но по мере роста капиталовооруженности темп ее роста постепенно снижается и точке пересечения и становиться равной нулю. Таким образом, в долгосрочной перспективе повышение нормы сбережения не влияет на темпы роста капиталовооруженности и выпуска, но влияет на темпы роста в процессе движения к новому стационарному состоянию.
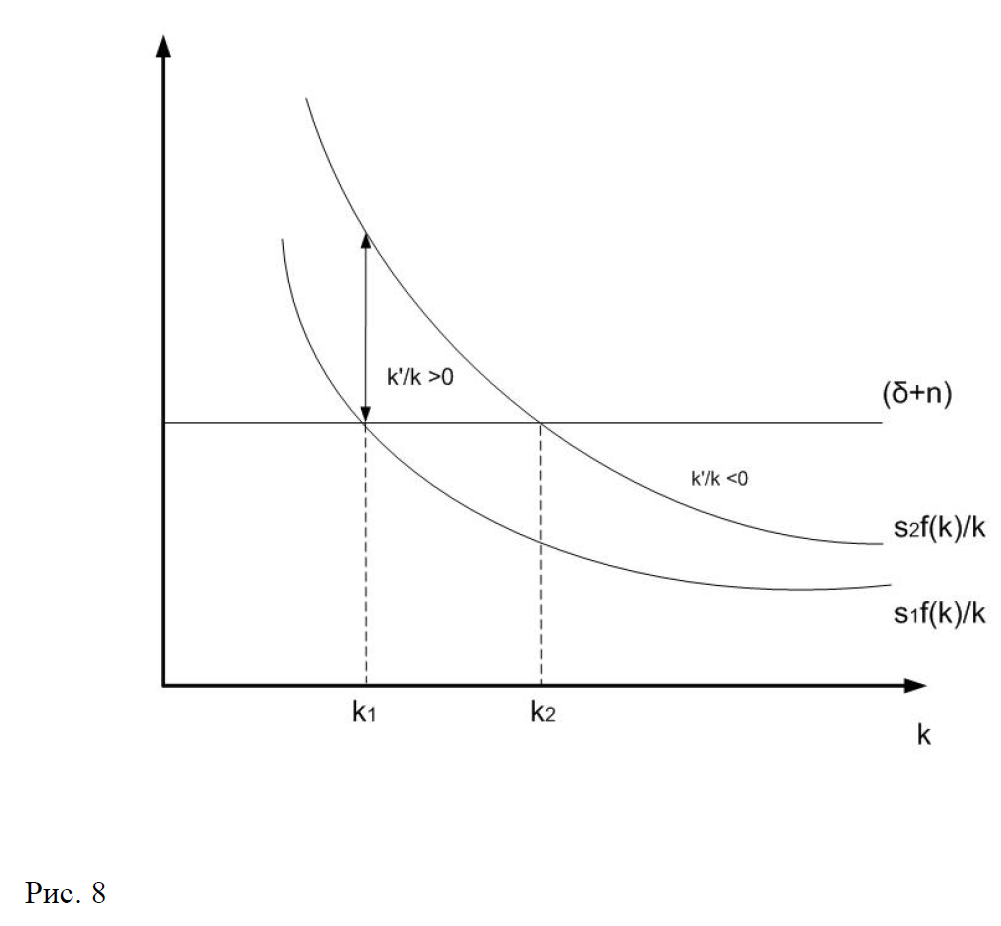
б. Изменение темпов роста населения
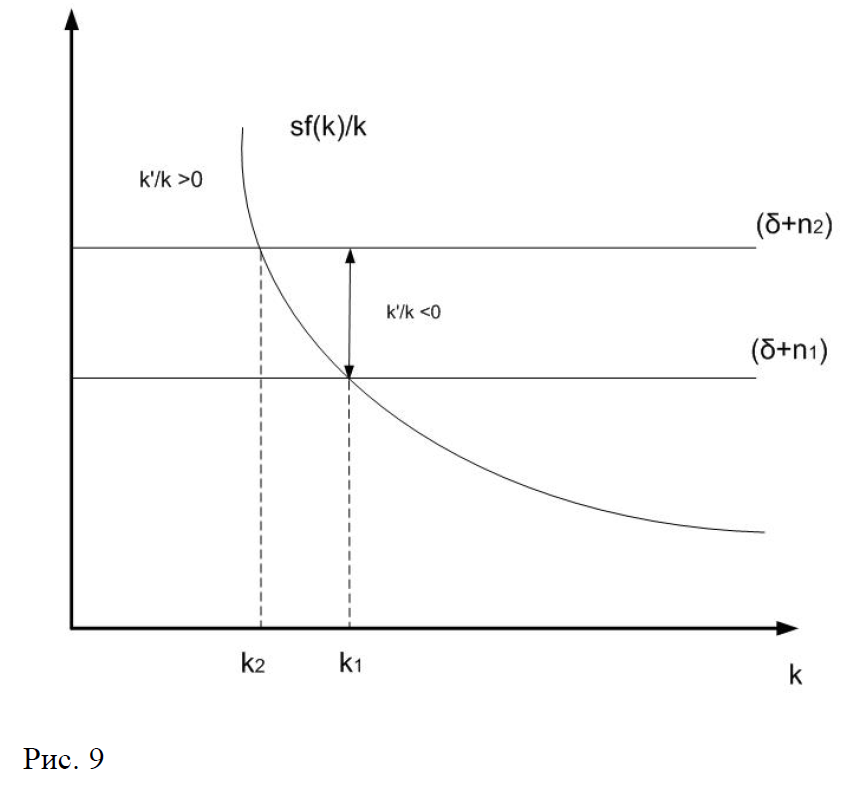
При повышении темпов роста населения с до nP_2 стационарная капиталовооруженность уменьшается с до , а темпы ее роста скачком уменьшаются до некоторого отрицательного значения. Экономика начинает двигаться так, что капиталовооруженность начинает падать, а темп ее роста увеличиваться. Это происходит до тех пор пока не будет достигнута новая стационарная точка , здесь темп рост капиталовооруженности становится равным нулю. (рис.9). Аналогичную динамику демонстрирует и производительность труда.
Если имеется группа стран с одинаковыми нормами сбережения и амортизации капитала, темпом роста населения и одинаковыми технологиями, то они имеют одну и ту же стационарную капиталовооруженность. При этом каждая из
стран может иметь различные текущие значения капиталовооруженности. Согласно модели Солоу, чем дальше отстоит текущие значение капиталовооруженности от стационарного, тем более высокие темпы ее роста будут наблюдаться.
Следовательно, отстающие страны будут догонять передовые, т.е должна иметь место абсолютная конвергенция.
Но на практике этого не наблюдается, так как разные страны имеют разные нормы сбережения и амортизации, темпы роста населения и технологии, а значит и разные стационарные точки. При этом, те страны текущие значение капиталовооруженности которых дальше отстает от их стационарных значений, должны развиваться быстрее, т.е. имеет место относительная конвергенция.
Ниже представлен скрипт исследования удельной дискретной модели Солоу без НТП, который позволяет:
-
Рассчитать значение капиталовооруженности в стационарной точке и точке, соответствующей золотому правилу накопления капитала (для этого используются соотношения 25 и 29).
-
Строить графики y(t), k(t), inv(t), c(t).
-
Строить график движения экономики к стационарной точке и графически определяет ее (рис. 3).
-
Строить графики, позволяющие графически определить точку ,соответствующую золотому правилу накопления капитала (рис. 4)
-
Строить графики, описывающие темпы прироста капиталовооруженности при разных нормах сбережения (рис. 8).
-
Строить графики, описывающие темпы прироста производительности труда при разных нормах сбережения.
using Plots, PlotThemes
using StatsBase
#УДЕЛЬНАЯ МОДЕЛЬ СОЛОУ БЕЗ НТП ДИСКРЕТНЫЙ ВАРИАНТ
#ЗАДАНИЕ ИСХОДНЫХ ДАННЫХ
#горизонт прогноза
T = 100;
#норма амортизации капитала
δ = 0.3;
#норма сбережения
s = 0.8;
#темп роста труда
n = 0.01;
#эластичность выпуска по капиталу
α = 0.7;
# производственная функция f= k(t)^α
#РАСЧЕТ СТАЦИОНАРНОЙ ТОЧКИ
b=α-1;
h=(n+δ)/s;
ks=h^(1/b);
ks=round.(ks, sigdigits=4);
#РАСЧЕТ НОРМЫ СБЕРЕРЕЖЕНИЯ ДЛЯ ЗОЛОТОГО ПРАВИЛА
h1 =(n + δ)/α;
kg=h1^(1/b);
sg = (kg * (n + δ)) / kg^α;
kg = round.(kg, sigdigits=4);
#МОДЕЛИВАНИЕ ДИНАМИКИ ЭКОНОМИКИ ПО ДИСКРЕТНОЙ МОДЕЛИ СОЛОУ И ЕЕ ГРАФИЧЕСКИЙ АНАЛИЗ
#начальное значение
y = zeros(T + 1)
c = zeros(T + 1)
iv = zeros(T + 1)
k = zeros(T + 1)
t = 1;
k[t] = 0.1;
#Расчет эндогенных переменных модели для t
#выпуск
y[t] = k[t]^α
#потребление
c[t] = (1 - s) * y[t];
#инвестиции
iv[t] = s * y[t];
#рост капиталовооруженности
k[t+1] = s * y[t] + (1 - δ)*k[t]
for t in (2:T)
y[t] = k[t]^α
c[t] = (1 - s) * y[t]
iv[t] = s * y[t]
k[t+1] = s * y[t] + (1 - δ) * k[t]
end
t = 1:T
#ГРАФИКИ ДВИЖЕНИЯ ВО ВРЕМЕНИ ПАРАМЕТРОВ ЭКОНОМИКИ СОЛЛОУ
plotly()
theme(:dao)
p1=plot(t, y[1:T], title="y , c , inv ", ylabel="y,c,inv", xlabel="t", label="Производство на душу", lw=2)
plot!(t, c[1:T], label="Потребление на душу", lw=3)
plot!(t, iv[1:T], label="Инвестиции на душу", lw=3, wsize=(800, 500))
plot!(t, k[1:T], label="Капиталовооруженность", lw=3)
#ГРАФИЧЕСКОЕ ОПРЕДЕЛЕНИЕ СТАЦИОНАРНОЙ ТОЧКИ ЭКОНОМИКИ СОЛОУ
y1 = s * y;
y2 = (n + δ) * k;
p2 = plot(k[1:T], y[1:T], title="Стационарное состояние экономики k*= $ks", label="y", xlabel="k", lw=3)
plot!(k[1:T], y1[1:T], label="sy", lw=3, ylabel="y, sy, (n + δ)k")
plot!(k[1:T], y2[1:T], label="(n+δ)", lw=3)
plot!([ks], [s * ks^α], label="k*",
seriescolor=:red,
marker=:circle,
markersize=6,
markercolor=:red,
markerstrokecolor=:red
)
#ГРАФИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ЗОЛОТОГО ПРАВИЛА ЭКОНОМИКИ СОЛОУ
s0 = sg - 0.1;
s1 = sg;
s2 = sg + 0.1;
y11 = s0 * y;
y12 = s1 * y;
y13 = s2 * y;
p3 = plot(k[1:T], y[1:T], title="Золотое правило экономики kg= $kg", label="y", lw=3,lc=:blue1,xlabel="k")
plot!(k[1:T], y2[1:T], label="s0y", lc=:coral, lw=3)
plot!(k[1:T], y11[1:T], label="s1y", lc=:cyan, lw=3)
plot!(k[1:T], y12[1:T], label="s2y", lc=:firebrick, lw=3)
plot!(k[1:T], y13[1:T], label="(n + δ)k", lc=:khaki, lw=3)
plot!([kg], [sg * kg^α], label="kg",
seriescolor=:green,
marker=:circle,
markersize=6,
markercolor=:green,
markerstrokecolor=:green
)
plot(p2, p3, layout=(1, 2), wsize=(1000, 400), legend=:outertopright)
#ДОЛГОСРОЧНАЯ ДИНАМИКА КАПИТАЛОВООРУЖЕННОСТИ И ПРОИЗВОДИТЕЛЬНОСТИ ТРУДА
nd = zeros(T + 1)
t = 1;
nd[t] = (n + δ);
for t in 2:1:T
nd[t] = (n + δ)
end
kk0 = s0 * y ./ k;
kk1 = s1 * y ./ k;
kk2 = s2 * y ./ k;
yy0 = α * (kk0 - nd);
yy1 = α * (kk1 - nd);
yy2 = α * (kk2 - nd);
s2=round.(s2, sigdigits=3)
p4=plot(k[1:T], kk0[1:T], title="Темп роста капиталовооруженности",label="s0= $s0", lw=3,lc=:blue1,xlabel="k")
plot!(k[1:T], kk1[1:T], label="s1= $s1", ylabel="dk/dt/k)", lw=3, lc=:coral)
plot!(k[1:T], kk2[1:T], label="s2= $s2", lw=3, lc=:cyan)
plot!(k[1:T], nd[1:T], label="(n + δ)=$(n + δ)", lw=4, lc=:red)
p5=plot(k[1:T], yy0[1:T], title="Темп роста производительности труда",label="s0= $s0", lw=3,xlabel="k")
plot!(k[1:T], yy1[1:T], label="s1= $s1", ylabel="dy/dt/y", lw=3, xlabel="k")
plot!(k[1:T], yy2[1:T], label="s2= $s2", lw=3 )
plot(p4, p5, layout=(1, 2), wsize=(1000, 400), legend=:outertopright)
4. Модель Солоу с трудосберегающим техническим прогрессом (AL-модель).
До сих пор в модели технология считалась неизменной, следовательно, капиталовооруженность и производительность трудав долгосрочной перспективе также являются неизменными, что противоречит экономическим реалиям. Для того,
чтобы учесть тот факт, что технологии под влиянием НТП постоянно меняются, необходимо учитывать влияние НТП в модели. Учесть это влияние можно разными способами, что приводит к разным типам НТП: нейтральный, капиталосбере
гающий и трудосберегающий. Нейтральный НТП позволяет произвести продукцию при меньших затратах капитала и труда:
Капиталосберегающий НТП увеличивает выпуск за счет повышения эффективности использования капитала:
Трудосберегающий НТП увеличивает выпуск за счет повышения эффективности использования труда:
Если считать НТП имеет постоянный темп роста:
То только трудосберегающий НТП обеспечивает существование стационарного состояния экономики.
Запишем условие равновесия с учетом трудосберегающего НТП:
Перепишем условие (39) для одного эффективного работника:
Введем обозначения , и после целого ряда приобразований (они нами здесь опущены) получим основное уравнение удельной AL модели Солоу:
Уравнение (41) описывает накопление капитала при наличии трудосберегающего НТП. Стационарное состояние при котором определяется из условия:
В стационарном состоянии капитал на одного эффективного работника постоянен, следовательно, и тоже постоянны. А так как , то капиталовооруженность, производительность труда и потребление в стационарном состоянии должны расти с темпом НТП. При этом
запас капитала и уровень выпуска в стационарном состоянии растут с темпом . Норма сбережения, норма амортизации и производственная функция влияют только на траекторию перехода к стационарному состоянию, но не влияют на темпы роста в стационарном состоянии.
Таким образом, темп роста экономики выпуск на душу населения при полной занятости в модели Солоу полностью определяется темпом роста НТП. Но из этой модели остается полностью непонятным, чем определяется темп самого
НТП.
Ниже представлены реализации удельной AL модели Солоу в дискретном и непрерывном вариантах в виде скриптов Julia и динамических моделей Engee.
using Plots, PlotThemes
using StatsBase
#УДЕЛЬНАЯ МОДЕЛЬ СОЛОУ С ТРУДОСБЕРЕГАЮЩИМ НТП ДИСКРЕТНЫЙ ВАРИАНТ
#ЗАДАНИЕ ИСХОДНЫХ ДАННЫХ
#горизонт прогноза
T=100;
#норма амортизации капитала
δ=0.25;
#норма сбережения
s=0.55;
# темп роста труда
n=0.02;
#темп роста прогресса
g=0.005;
#коэффициент эластичности капитала
α=0.7;
y = zeros(T + 1)
c = zeros(T + 1)
iv = zeros(T + 1)
k = zeros(T + 1)
t=1;
k[t]=0.1;
#Расчет эндогенных переменных модели для t
#выпуск
y[t]=k[t]^α;
#потребление
c[t]=(1-s)*y[t];
#инвестиции
iv[t]=s*y[t];
#прирост капиталовооруженности
k[t+1]=s*y[t]+(1-(δ+n+g))*k[t];
for t in 2:1:T
t;
y[t]=k[t]^α;
c[t]=(1-s)*y[t];
iv[t]=s*y[t];
k[t+1]=s*y[t]+(1-(δ+n+g))*k[t];
end
t = 1:T
plotly()
theme(:dao)
plot(t, y[1:T], title="y , c , inv ", ylabel="y, c, inv, k", xlabel="t", label="Объем производства на душу", lw=2)
plot!(t, c[1:T], label="Потребление на душу", lw=3)
plot!(t, iv[1:T], label="Инвестиции на душу", lw=2, wsize=(700, 400))
plot!(t, k[1:T], label="Капиталовооруженность", lw=3)
using DifferentialEquations, Plots, PlotThemes
using StatsBase
#УДЕЛЬНАЯ МОДЕЛЬ СОЛОУ С ТРУДОСБЕРЕГАЮЩИМ НТП НЕПРЕРЫВНЫЙ ВАРИАНТ
#ЗАДАНИЕ ИСХОДНЫХ ДАННЫХ
#начальная численность населения
@show N0=50;
#норма амортизации капитала
@show δ=0.25;
#норма сбережения
@show s=0.6;
# темп роста труда
@show n=0.03;
#темп роста прогресса
@show g=0.02;
#коэффициент эластичности капитала
@show α=0.7;
#начальная капиталовооруженность
@show k0=1.0;
#начальное значение А
@show A0=1.0;
#РАСЧЕТ СТАЦИОНАРНОЙ ТОЧКИ
b=α-1;
h=(n+δ+g)/s;
@show ks=h^(1/b);
#РАСЧЕТ НОРМЫ СБЕРЕРЕЖЕНИЯ ДЛЯ ЗОЛОТОГО ПРАВИЛА
α=0.7;
h1 = (n + δ + g)/α;
@show kg=h1^(1/b);
sg = (kg*(n + δ + g))/kg^α
function solou1!(du, u, p, t)
α , s, n, δ, g = p
du[1] = s * u[1]^α - u[1]*(n+δ+g)
end
u0 = [k0]
p = (α, s, n, δ, g)
tspan = (0.0, 100.0)
prob = ODEProblem(solou1!, u0, tspan, p)
sol = solve(prob, reltol=1e-8, abstol=1e-8)
# расчет y(t)
yA = zeros(length(sol[:, :]))
y = zeros(length(sol[:, :]))
yA = sol[1, :] .^ α
At = @.exp(g * sol.t) * A0
y = yA .* At
#расчет k(t)
k = zeros(length(sol[:, :]))
k= sol[1, :].*At
#расчет c(t)
c = zeros(length(sol[:, :]))
c =(1-s).*y
#расчет N(t)
N =zeros(length(sol[:, :]))
N = @.N0*exp(sol.t[:, 1]*n)
#расчет Y(t)
Y = zeros(length(sol[:, :]))
Y=@.yA*At*N
#расчет K(t)
K = zeros(length(sol[:, :]))
K = @.sol[1, :] * At * N
plotly()
theme(:dao)
p1=plot(sol, linewidth=2, title="Кап.вооруженность эфф.работника",label="kA(t)", lc=:blue)
p2 = plot(sol.t[:, 1], y, linewidth=2, title="Производительность труда", label="y(t)", lc=:brown)
p3 = plot(sol.t[:, 1], k, linewidth=2, title="Капиталовооруженность", label="k(t)", lc=:coral)
p4 = plot(sol.t[:, 1], c, linewidth=2, title="Потребление на душу", label="c(t)", lc=:crimson)
p5 = plot(sol.t[:, 1], Y, linewidth=2, title="Валовой доход", label="Y(t)", lc=:fuchsia, xlabel="t")
p6 = plot(sol.t[:, 1], K, linewidth=2, title="Масса капитала", label="K(t)", lc=:lawngreen, xlabel="t")
plot(p1, p2,p3,p4, p5, p6, layout=(3, 2), wsize=(900, 600), legend=:outertopright)
# расчет dy(t)/y
yy = zeros(length(sol[:, :]))
YY = zeros(length(sol[:, :]))
kk = zeros(length(sol[:, :]))
KK = zeros(length(sol[:, :]))
for i in 2:length(sol[:, :])
global Δt = sol.t[i, 1] - sol.t[(i-1), 1]
global Δy =y[i]-y[i-1]
global dy = Δy / Δt
yy[i]=dy/y[i]
global ΔY = Y[i] - Y[i-1]
global dY = ΔY/ Δt
YY[i] = dY /Y[i]
global Δk = k[i] - k[i-1]
global dk = Δk/ Δt
kk[i] = dk / k[i]
global ΔK = K[i] - K[i-1]
global dK = ΔK / Δt
KK[i] = dK / K[i]
end
yy
p7=plot(sol.t[2:end, 1], yy[2:end], linewidth=2, title="Темп прироста производительности труда",
label="dy(t)/y(t)", lc=:lawngreen)
p8=plot(sol.t[2:end-1, 1], YY[2:end-1], linewidth=2, title="Темп прироста дохода",
label="dY(t)/Y(t)", lc=:red)
p9 = plot(sol.t[2:end, 1], kk[2:end], linewidth=2, title="Темп прироста капиталовооруженности",
label="dk(t)/k(t)", lc=:black, xlabel="t")
p10 = plot(sol.t[2:end-1, 1], KK[2:end-1], linewidth=2, title="Темп прироста капитала",
label="dK(t)/K(t)", lc=:brown, xlabel="t")
plot(p7, p8, p9, p10,layout=(2, 2), wsize=(900, 550), legend=:outertopright)
Переходные процессы в AL модели Солоу
Модифицируем AL-модель, полученную выше, таким образом, чтобы она позволяла моделировать переходные процессы в экономике Солоу, возникающие при скачкообразном изменении нормы сбережения в некоторый момент t.
using DifferentialEquations, Plots, PlotThemes
using StatsBase
#УДЕЛЬНАЯ МОДЕЛЬ СОЛОУ С ТРУДОСБЕРЕГАЮЩИМ НТП НЕПРЕРЫВНЫЙ ВАРИАНТ
#ПЕРЕХОДНЫЕ ПРОЦЕССЫ ПРИ ИЗМЕНЕНИИ s
#ЗАДАНИЕ ИСХОДНЫХ ДАННЫХ
#начальная численность населения
@show N0 = 50;
#норма амортизации капитала
@show δ = 0.25;
# темп роста труда
@show n = 0.03;
#темп роста прогресса
@show g = 0.02;
#коэффициент эластичности капитала
@show α = 0.7;
#начальная капиталовооруженность
k0 = 1.0;
#начальное значение А
@show A0 = 1.0;
#норма сбережения
@show s = 0.6;
s1=s
function solou50!(du, u, p, t)
α,s, n, δ, g = p
du[1] = s * u[1]^α - u[1] * (n + δ + g)
end
u0 = [k0]
p = (α,s, n, δ, g)
tspan50 = (0.0, 50.0)
prob50 = ODEProblem(solou50!, u0, tspan50, p)
sol50 = solve(prob50, reltol=1e-8, abstol=1e-8)
t1 = sol50.t[:, 1]
kA1 = sol50[1, :]
# расчет y1(t)
yA1 = zeros(length(sol50[:, :]))
y1 = zeros(length(sol50[:, :]))
yA1 = kA1.^ α
At1 = @.exp(g * sol50.t) * A0
y1 = yA1 .* At1
#расчет k1(t)
k1 = zeros(length(sol50[:, :]))
k1 = kA1 .* At1
#расчет c1(t)
c1 = zeros(length(sol50[:, :]))
c1 = (1 - s) .* y1
#расчет N1(t)
N1 = zeros(length(sol50[:, :]))
N1 = @.N0 * exp(sol50.t[:, 1] * n)
#расчет Y(t)
Y1 = zeros(length(sol50[:, :]))
Y1 = @.yA1 * At1 * N1
#расчет K1(t)
K1 = zeros(length(sol50[:, :]))
K1 = @.sol50[1, :] * At1 * N1
#изменение в точке t=50.0 s=s-0.3
function solou100!(du, u, p, t)
α, s, n, δ, g = p
du[1] = s * u[1]^α - u[1] * (n + δ + g)
end
u0 = [kA1[end]]
@show s=s-0.3; #изменение нормы сбережения s
s2 =s
p = (α, s, n, δ, g)
tspan100 = (50.0, 100.0)
prob100 = ODEProblem(solou100!, u0, tspan100, p)
sol100 = solve(prob100, reltol=1e-8, abstol=1e-8)
t2 = sol100.t[:, 1]
kA2 = sol100[1, :]
# расчет y2(t)
yA2 = zeros(length(sol100[:, :]))
y2 = zeros(length(sol100[:, :]))
yA2 = kA2 .^ α
At2 = @.exp(g * sol100.t) * A0
y2 = yA2 .* At2
#расчет k2(t)
k2 = zeros(length(sol100[:, :]))
k2 = kA2 .* At2
#расчет c2(t)
c2 = zeros(length(sol100[:, :]))
c2 = (1 - s) .* y2
#расчет N2(t)
N2 = zeros(length(sol100[:, :]))
N2 = @.N0 * exp(sol100.t[:, 1] * n)
#расчет Y2(t)
Y2 = zeros(length(sol100[:, :]))
Y2 = @.yA2 * At2 * N2
#расчет K2(t)
K2 = zeros(length(sol100[:, :]))
K2 = @.sol100[1, :] * At2 * N2
p1=plot(t1,kA1,linewidth=2, title="kA ", label="s= $s1", lc=:blue)
plot!(t2,kA2,linewidth=2, label="s= $s2", lc=:red)
p2 = plot(t1, y1, linewidth=2, title="y",label="s= $s1", lc=:blue)
plot!(t2, y2, linewidth=2,label="s= $s2",lc=:red)
p3 = plot(t1, k1, linewidth=2, title="k", label="s= $s1",legend=false, lc=:blue)
plot!(t2, k2, linewidth=2, label="s= $s2", lc=:red)
p4 = plot(t1, c1, linewidth=2, title="c", label="s= $s1", lc=:blue)
plot!(t2, c2, linewidth=2, label="s= $s2", lc=:red)
p5 = plot(t1, Y1, linewidth=2, title="Y", label="s= $s1", lc=:blue)
plot!(t2, Y2, linewidth=2, label="s= $s2", lc=:red)
p6 = plot(t1, K1, linewidth=2, title="K", label="s= $s1", lc=:blue)
plot!(t2, K2, linewidth=2, label="s= $s2", lc=:red)
plot(p1, p2, p3, p4, p5, p6, layout=(3, 2), wsize=(900, 750), legend=false)
Реализация AL-модели Солоу на Engee
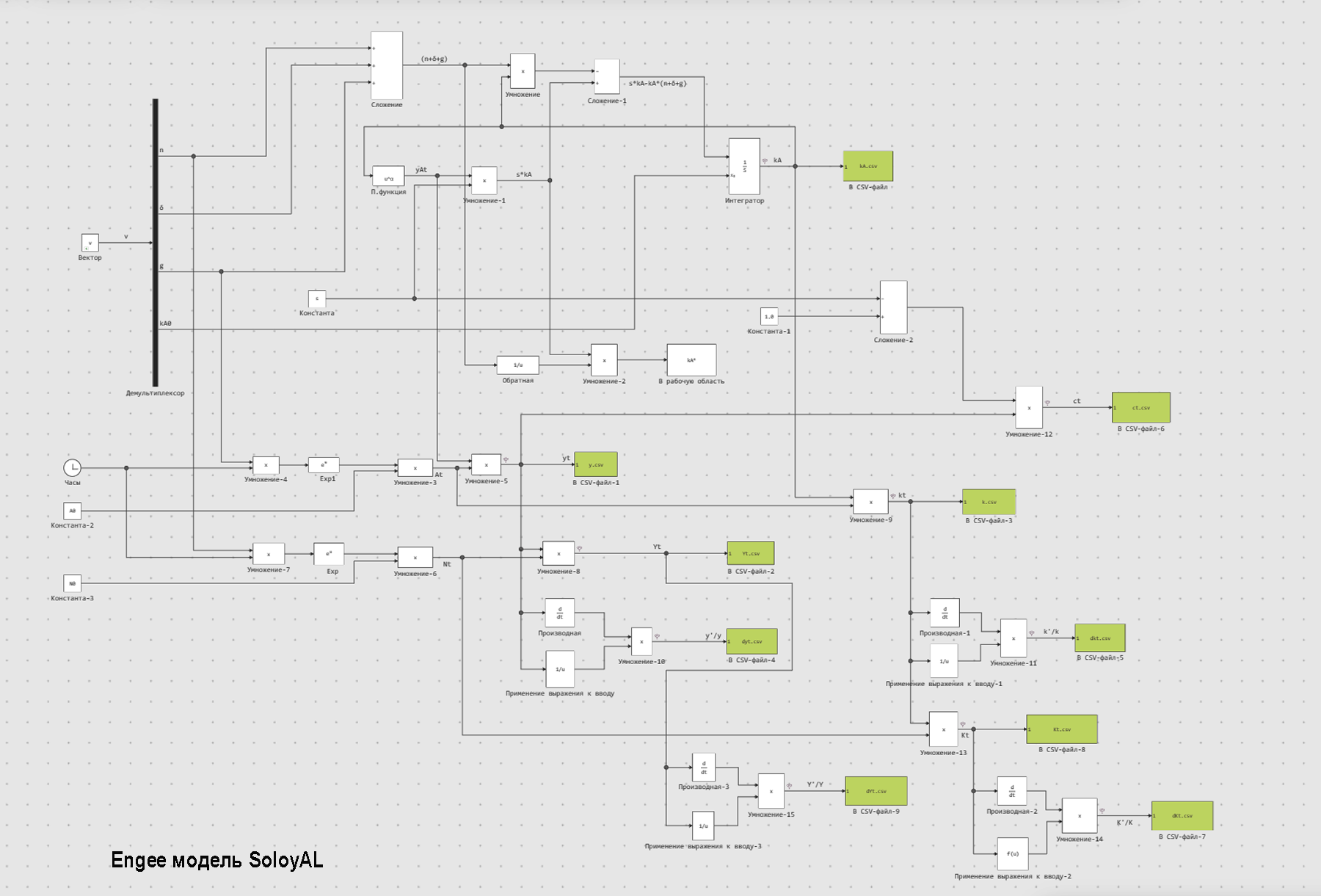
#УДЕЛЬНАЯ МОДЕЛЬ СОЛОУ С ТРУДОСБЕРЕГАЮЩИМ НТП НЕПРЕРЫВНЫЙ ВАРИАНТ
using RDatasets, Plots, PlotThemes
using CSV, DataFrames
#Солоу AL- модель
#открытие модели
modelName = "SoloyAL";
PID_model = modelName in [m.name for m in engee.get_all_models()] ? engee.open(modelName) :
engee.load("/user/ModRost/$(modelName).engee");
engee.set_param!(modelName, "StopTime" => 100.0) # задание интервала моделирования
#ЗАДАНИЕ ИСХОДНЫХ ДАННЫХ
#начальная численность населения
@show N0 = 50;
#норма амортизации капитала
@show δ = 0.25;
# темп роста труда
@show n = 0.03;
#темп роста прогресса
@show g = 0.02;
#коэффициент эластичности капитала
@show α = 0.7;
#начальная капиталовооруженность
kA0 = 1.0;
#начальное значение А
@show A0 = 1.0;
#норма сбережения
@show s = 0.6;
@show v=[n, δ, g, kA0];
engee.run(modelName) #запуск модели
df_kAt = CSV.read("kA.csv", DataFrame)
df_kt = CSV.read("k.csv", DataFrame)
df_yt = CSV.read("y.csv", DataFrame)
df_dkt = CSV.read("dkt.csv", DataFrame)
df_dyt = CSV.read("dyt.csv", DataFrame)
df_ct = CSV.read("ct.csv", DataFrame)
df_Kt = CSV.read("Kt.csv", DataFrame)
df_Yt = CSV.read("Yt.csv", DataFrame)
df_dKt = CSV.read("dKt.csv", DataFrame)
df_dYt = CSV.read("dYt.csv", DataFrame);
plotly()
theme(:dao)
p1 = plot(df_kAt[!,"time"], df_kAt[!,"1"],lw=2, title="Кап.вооруженность эфф.работника",label="kA(t)", lc=:blue)
p2 = plot(df_yt[!, "time"], df_yt[!, "1"], lw=2, title="Производительность труда", label="y(t)", lc=:brown)
p3 = plot(df_kt[!, "time"], df_kt[!, "1"],lw=2, title="Капиталовооруженность", label="k(t)", lc=:coral)
p4 = plot(df_ct[!, "time"], df_ct[!, "1"],lw=2, title="Потребление на душу", label="c(t)", lc=:crimson)
p5 = plot(df_Yt[!, "time"], df_Yt[!, "1"],lw=2, title="Валовой доход", label="Y(t)", lc=:fuchsia, xlabel="t")
p6 = plot(df_Kt[!, "time"], df_Kt[!, "1"],lw=2, title="Масса капитала", label="K(t)",lc=:lawngreen, xlabel="t")
plot(p1, p2, p3, p4, p5, p6, layout=(3, 2), wsize=(900, 600), legend=:outertopright)
p7=plot(df_dyt[!, "time"], df_dyt[!, "1"], lw=2,title="Темп прироста производительности труда",
label="dy(t)/y(t)", lc=:lawngreen)
p8=plot(df_dYt[!, "time"], df_dYt[!, "1"], lw=2, title="Темп прироста дохода",
label="dY(t)/Y(t)", lc=:red)
p9 = plot(df_dkt[!, "time"], df_dkt[!, "1"], lw=2, title="Темп прироста капиталовооруженности",
label="dk(t)/k(t)", lc=:black, xlabel="t")
p10 = plot(df_dKt[!, "time"], df_dKt[!, "1"], lw=2, title="Темп прироста капитала",
label="dK(t)/K(t)", lc=:brown, xlabel="t")
plot(p7, p8, p9, p10, layout=(2, 2), wsize=(900, 550), legend=:outertopright)
Выводы
Модель Солоу дала необходимую математическую базу для анализа темпов изменения капитала и экономического эффекта экономического прогресса, на которой в дальнейшем исследователи создали множество более сложных моделей, потому её считают отправной точкой для всех современных исследований экономического роста. Модель оказала влияние на всю макроэкономическую теорию
Но вместе с тем модель не могла дать объяснение многим проблемам, связанным с экономическим ростом. С теоретической точки зрения, модель не показывает, каким образом решения домохозяйств влияют на норму сбережения и, вместе с решениями фирм, на темпы экономического роста. Параметры нормы сбережений и темпов научно-технического прогресса в модели просто задаются экзогенно, решения экономических агентов на них никак не влияют, что не устраивало исследователей. Более того, даже сильная сторона модели — процесс накопления капитала — по сути представляет собой «чёрный ящик», механизм влияния на который экономических агентов в модели не раскрыт.Эмпирическая проверка ряда положений модели показала, что они не находят подтверждения на практике.Она не объясняет, почему бедные страны в большинстве случаев остаются бедными и не могут догнать богатые.
Модель Мэнкью – Ромера – Вейла экономического роста с человеческим капиталом
Краткие теоретические основания модели
Понятие «человеческий капитал» впервые было введено в экономическую науку и его теоретические основы были разработаны лауреатами Нобелевской премии Гэри Беккером и Теодором Шульцем [Becker, 1964; Schulz, 1963].
Человеческий капитал — это оценка воплощенной в индивидууме способности приносить доход, сумму способностей, знаний, квалификации и навыков отдельного работника. Человеческий капитал зависит как от врожденных способностей и талантов, так и от полученного образования и тренинга. Как и физический, человеческий капитал способен накапливаться и амортизироваться (вследствие смертности, дисквалификации и т.д.).
Под инвестициями в человеческий капитал понимается «деятельность,которая влияет на будущий денежный и психический доход посредством увеличения ресурсов человека» [Becker, 1964]. Наиболее простым способом определения роли человеческого капитала как фактора производства и значения процесса его накопления является
введение человеческого капитала в базовую модель экзогенного роста Солоу, как особого фактора, наряду с физическим капиталом и трудом, определяющим объем выпуска в производственной функции.
Базовые предпосылки модели
В модели Мэнкью — Ромера—Вейла человеческий капитал выступает как производственный фактор и процесс его накопления полностью аналогичен физическому капиталу. При этом рассматривается закрытая экономика. Фирмы максимизируют свою прибыль. Фирмы функционируют в условиях совершенной конкуренции. Производится только один продукт , используемый, как для потребления , так и для инвестиций . Темпы технологического прогресса , роста населения и норма выбытия капитала (как человеческого, так и физического)
— постоянны и задаются экзогенно. В модели присутствуют две нормы сбережений для физического ()
и человеческого капитала () обе они задаются экзогенно, фискальная политика (государственные расходы и налоги) в модели отсутствует. Время изменяется непрерывно.
Предпосылка о закрытой экономике означает, что произведённый продукт тратится на инвестиции в физический и человеческий капитал, и потребление, экспорт/импорт отсутствуют, сбережения равны инвестициям:
Производственная функция удовлетворяет неоклассическим предпосылкам:
- технологический прогресс увеличивает производительность труда (нейтрален по Харроду)
где -физический капитал, -человеческий капитал, -труд, -параметр технологического прогресса в момент времени .
- производственная функция обеспечивает постоянную отдачу от масштаба:
- предельная производительность факторов положительная и убывающая:
- производственная функция удовлетворяет условиям Инады, а именно, если количество одного из факторов бесконечно мало, то его предельная производительность бесконечно велика, если же количество одного из факторов бесконечно велико, то его предельная производительность бесконечно мала:
- производству необходим каждый фактор:
Население , равное в модели совокупным трудовым ресурсам, растёт с постоянным темпом
:
Для поиска решения модели и его анализа используются удельные показатели: выпуск на единицу эффективного труда
, объем физического капитала на единицу эффективного труда , объем человеческого капитала на единицу эффективного труда ,потребление на единицу эффективного труда , инвестиции на единицу эффективного труда .
Тогда производственную функцию можно записать в следующем виде:
Наиболее часто в качестве конкретного примера производственной функции, удовлетворяющей предпосылкам модели, используется производственная функция Кобба — Дугласа:
где -эластичность выпуска по физическому капиталу, -эластичность выпуска по человеческому капиталу, - эластичность выпуска по труду.
Как и в модели Солоу, поведение потребителей в явном виде в модели не рассматривается. Функция полезности отсутствует. Вместо этого имеется две экзогенно задаваемые нормы сбережений физического и человеческого капитала и , , , ,означающие, что домохозяйства сберегают долю своего дохода ,а оставшуюся долю тратят на потребление, и это соотношение не зависит от происходящих в экономике событий
Основные уравнения модели и их анализ
Стационарное состояние в модели
Исходя из принципов построения модели, в каждый момент времени физический и человеческий капитал увеличиваются на величину инвестиций, то есть на и соответственно, и уменьшаются на и , таким образом, мы можем записать производные по времени физического капитала и человеческого капитала в следующем виде:
Учитывая, что и , производные по времени капиталовооружённости труда единицы эффективного труда и объема человеческого капитала на единицу эффективного труда , а также что
и получаем следующую основную систему дифференциальных уравнений модели:
Если инвестиции на единицу эффективного труда в физический и человеческий капитал превышают выбытие капитала на единицу эффективного труда и соответственно, то и растут, в противном случае — снижаются.
В стационарном состоянии, в котором уровень физического и человеческого капитала на единицу эффективного труда постоянны, и, соответственно, и , устойчивые уровни капиталовооружённости труда на единицу эффективного труда и запаса человеческого капитала на единицу эффективного труда определяются системой уравнений(12):
Если в модели в качестве производственной функции используется функция Кобба — Дугласа
, то и будут равны:
Графически достижение стационарного состояния в модели Мэнкью — Ромера — Вейла можно проиллюстрировать на графиках и , которые пересекают ось абсцисс в точках и соотвественно.
В итоге, в модели из любой начальной точки при система приходит к равновесию.
В стационарном состоянии темп прироста показателей на единицу эффективного труда равен нулю:
Показатели на единицу труда растут с темпом технологического прогресса :
Валовые показатели растут с темпом равным сумме темпов прироста технологического прогресса
и населения :
Оптимальный уровень нормы сбережений (Золотое правило)
Как и в модели Солоу, после нахождения устойчивых уровней и можно найти такие значения норм сбережений и , при котором в устойчивом состояние потребление на единицу эффективного труда максимально. То есть, необходимо решить задачу:
при условиях:
Выразив через и получим:
Тогда имеем:
В точке максимума и . С ростом нормы сбережений капиталовооружённость на единицу эффективного труда и запас человеческого капитала на единицу эффективного труда растут, потому и . Значит, в точке максимума должны выполняться равенства:
где — устойчивый уровень капиталовооружённости на единицу эффективного труда, — устойчивый уровень запаса человеческого капитала на единицу эффективного труда, соответствующие максимальному потреблению.
Таким образом, нормы сбережений и , максимизирующие потребление , находятся из решения системы уравнений:
В результате решения этой системы оптимальные нормы сбережения, соответствующие Золотому правилу, равны эластичностям выпуска по соответствующему вида капитала:
Если в качестве производственной функции в модели используется используется функция Кобба — Дугласа , у которой эластичности выпуска по физическому и человеческому капиталу постоянны, то и .
Практическая реализация модели Мэнкью – Ромера – Вейла на Julia.
Ниже представлен скрипт, позволяющий построить и исследовать модель для некоторого набора исходных экзогенных данных. Полученные графические результаты моделирования наглядно демонстрируют все теоретические возможности данной модели,рассмотренные выше, для оценки прогноза макроэкономического роста.
using DifferentialEquations, Plots, PlotThemes
using StatsBase
# Модель Мэнкью – Ромера – Вейла экономического роста с человеческим капиталом
#ЗАДАНИЕ ИСХОДНЫХ ДАННЫХ
#начальная численность населения
@show N0 = 50;
#норма амортизации капитала
@show δ = 0.25;
#норма сбережения физического капитала
@show sk = 0.4;
#норма сбережения человеческого капитала
@show sh = 0.5;
# темп роста труда
@show n = 0.01;
#темп роста прогресса
@show γ = 0.02;
#эластичность выпуска по физическому капиталу
@show α = 0.4;
#эластичность выпуска по человеческому капиталу
@show β = 0.5;
#начальная капиталовооруженность по физическому капиталу
@show kA0 = 0.1;
#начальная капиталовооруженность по человеческому капиталу
@show hA0 = 0.1;
#начальное значение А
@show A0 = 1.0;
#РАСЧЕТ СТАЦИОНАРНОЙ ТОЧКИ
kst= ((sk^(1 - β) * sh^β) / (n + δ + γ))^(1/(1 - α - β))
hst = ((sk^α * sh^(1-α)) / (n + δ + γ))^(1 / (1 - α - β))
@show kst=round.(kst, sigdigits=4);
@show hst = round.(hst, sigdigits=4);
#РАСЧЕТ НОРМЫ СБЕРЕРЕЖЕНИЯ ДЛЯ ЗОЛОТОГО ПРАВИЛА
skg = α
shg = β
sk = skg
sh = shg
function solou1!(du, u, p, t)
α, β, sk, sh, n, δ, γ = p
du[1] = sk * u[1]^α * u[2]^β - (n + δ + γ)*u[1]
du[2] = sh * u[1]^α * u[2]^β - (n + δ + γ) * u[2]
end
u0 = [kA0,hA0]
p = (α, β, sk, sh, n, δ, γ)
tspan = (0.0, 300.0)
prob = ODEProblem(solou1!, u0, tspan, p)
sol = solve(prob, reltol=1e-8, abstol=1e-8)
# расчет y(t)
yA = zeros(length(sol[1, :]))
y = zeros(length(sol[1, :]))
yA = @.(sol[1, :] ^ α * sol[2, :] ^ β)
At = @.exp(γ * sol.t) * A0
y = yA .* At
#расчет k(t)
k = zeros(length(sol[1, :]))
k = sol[1, :] .* At
#расчет h(t)
h = zeros(length(sol[2, :]))
h = sol[2, :] .* At
#расчет c(t)
c = zeros(length(sol[1, :]))
cA = (1 - (sk + sh)) .* yA
dkA = @.(sk * sol[1, :]^α * sol[2, :]^β - (n + δ + γ) * sol[1, :])
dhA = @.(sh * sol[1, :]^α * sol[2, :]^β - (n + δ + γ) * sol[2, :])
plotly()
theme(:dao)
#theme(:ggplot2)
kA = [sol[1, :], sol[2, :]]
K = [k,h]
p1 = plot(sol.t, kA, title="капиталовооруженность kA,hA", label=["kA(t)" "hA(t)"],lw=3,
lc=["bisque4" "darkcyan"])
p2 = plot(sol.t, K, title="капиталовооруженность k,h", label=["k(t)" "h(t)"], lw=3, lc=["green" "red"])
p3 = plot(sol.t, y, title="производительность труда - y", label=("y(t)"), lw=3, lc=:aqua)
p4 = plot(sol.t, cA, title="потребление сA", label=("cA(t)"), lw=3, lc=:blueviolet)
p5 = plot(sol.t, dkA, title="dkA/dt, dhA/dt", label="dkA/dt", lw=3, lc=:brown)
plot!(sol.t, dhA, xlabel="t", label="dhA/dt", lw=3, lc=:burlywood4)
p6 = plot(sol[2, :], dhA, title="dhA/dt, dkA/dt", label="dhA/dt", lw=3, lc=:cadetblue4)
plot!(sol[1, :], dkA, xlabel="k,h", label="dkA/dt", lw=3, lc=:coral4)
plot!([kst], [0.0], label="kst= $kst",
seriescolor=:green,
marker=:circle,
markersize=4,
markercolor=:green,
markerstrokecolor=:green)
plot!([hst], [0.0], label="hst= $hst",
seriescolor=:green,
marker=:circle,
markersize=4,
markercolor=:red,
markerstrokecolor=:green)
plot(p1, p2, p3, p4, p5, p6, layout=(3, 2), wsize=(950, 850), legend=:outertopright)
#расчет N(t)
N = zeros(length(sol[1, :]))
N = @.N0 * exp(sol.t[:, 1] * n)
#расчет Y(t)
Y = zeros(length(sol[1, :]))
Y = @.yA * At * N
#расчет K(t)
K = zeros(length(sol[1, :]))
K = @.sol[1, :] * At * N
#расчет H(t)
H = zeros(length(sol[2, :]))
H = @.sol[2, :] * At * N;
theme(:dao)
p7 = plot(sol.t, Y, title="Доход Y", label="Y(t)", lw=3, lc=:blue)
p8 = plot(sol.t, K, title="Масса физ. капитала K", label="K(t)", lw=3, lc=:bisque4)
p9 = plot(sol.t, H, title="Масса чел. капитала H", label=("H(t)"), lw=3, lc=:aqua)
plot(p7, p8, p9, layout=(1, 3), wsize=(1000, 280),xlabel="t", legend=:outertopright)
#расчет темпов
yy = zeros(length(sol[1, :]))
YY = zeros(length(sol[1, :]))
kk = zeros(length(sol[1, :]))
KK = zeros(length(sol[1, :]))
hh = zeros(length(sol[1, :]))
HH = zeros(length(sol[1, :]))
for i in 2:length(sol[1, :])
global Δt = sol.t[i, 1] - sol.t[(i-1), 1]
global Δy = y[i] - y[i-1]
global dy = Δy / Δt
yy[i] = dy / y[i]
global ΔY = Y[i] - Y[i-1]
global dY = ΔY / Δt
YY[i] = dY / Y[i]
global Δk = k[i] - k[i-1]
global dk = Δk / Δt
kk[i] = dk / k[i]
global ΔK = K[i] - K[i-1]
global dK = ΔK / Δt
KK[i] = dK / K[i]
global Δh = h[i] - h[i-1]
global dh = Δh / Δt
hh[i] = dh / h[i]
global ΔH = H[i] - H[i-1]
global dH = ΔH / Δt
HH[i] = dH / H[i]
end
theme(:ggplot2)
p10 = plot(sol.t[2:end, 1], yy[2:end], linewidth=2, title="Темп прироста y",
label="dy(t)/y(t)", lc=:lawngreen)
p11 = plot(sol.t[2:end-1, 1], YY[2:end-1], linewidth=2, title="Темп прироста дохода Y",
label="dY(t)/Y(t)", lc=:red)
p12 = plot(sol.t[2:end, 1], kk[2:end], linewidth=2, title="Темп прироста k",
label="dk(t)/k(t)", lc=:black)
p13 = plot(sol.t[2:end-1, 1], KK[2:end-1], linewidth=2, title="Темп прироста капитала K",
label="dK(t)/K(t)", lc=:brown)
p14 = plot(sol.t[2:end-1, 1], hh[2:end-1], linewidth=2, title="Темп прироста h",
label="dh(t)/H(t)", lc=:green)
p15 = plot(sol.t[2:end-1, 1], HH[2:end-1], linewidth=2, title="Темп прироста капитала H",
label="dH(t)/H(t)", lc=:brown )
plot(p10, p11, p12, p13,p14, p15, layout=(2, 3), wsize=(1000, 500),xlabel="t", legend=:outertopright)
Использование модели Мэнкью – Ромера – Вейла для сравнения возможного роста экономик США и России (игрушечный пример)
Исходные экзогенные параметры, задающие начальные условия: начальная капиталовооруженность по физическому капиталу, начальная капиталовооруженность по человеческому капиталу, начальное значение А НТП.
Задаются следующим образом kA-США/kA-РФ = 0.8/0.2= 4, hA-США/hA-РФ = 0.7/0.25= 2.8, A-США/A-РФ= 10.0/2.0= 5.0. Демографические показатели: население N0-США/N0-РФ=346/150 =2.31 , темп роста нселения
n-США/n-РФ=0.025/0.002=12.5. Сруктура и параметры производственной функции (Кобба-Дугласа) считаются идентичными.Параметры сбережения капитала для США принимаются sk = 0.3,sh = 0.4. Это обеспечивает использование 30 % для потребления. Норма амортизации капитала в США 0.25 и темп роста прогресса 0.02
В качестве выходных параметров модели будем рассматривать доход на душу населения и валовой доход. Задача найти для России такие значения sk,sh,δ и γ, которые позволят России обойти США по доходу на душу населения за разумный срок 35-40 лет. Согласно модели это позволят сделать следующие показатели для России δ = 0.245,
sk = 0.44,sh2 = 0.41 (на потребление можно использовать только 15 % валового дохода) и γ = 0.030 (на 50% выше чем в США).В рамках существующей рыночной капиталистической экономики это обеспечить невозможно. К такой экономической и социальной политике можно приблизиться только при переходе к гибкой плановой экономике (новая индустрилизация со среднегодовым темпом роста 5-8 процентов с ограничением спекулитивного финансового капитала и избыточного потребления). Сейчас такой подход частично реализуется в сфере ВПК.
using DifferentialEquations, Plots, PlotThemes
using StatsBase
# Модель Мэнкью – Ромера – Вейла : страна лидер
#ЗАДАНИЕ ИСХОДНЫХ ДАННЫХ
#начальная численность населения
@show N10 = 346;
#норма амортизации капитала
@show δ1 = 0.25;
#норма сбережения физического капитала
@show sk1 = 0.3;
#норма сбережения человеческого капитала
@show sh1 = 0.4;
# темп роста труда
@show n1 = 0.025;
#темп роста прогресса
@show γ1 = 0.020;
#эластичность выпуска по физическому капиталу
@show α1 = 0.40;
#эластичность выпуска по человеческому капиталу
@show β1 = 0.48;
#начальная капиталовооруженность по физическому капиталу
@show kA10 = 0.8;
#начальная капиталовооруженность по человеческому капиталу
@show hA10 = 0.7;
#начальное значение А
@show A10 = 10.0;
#РАСЧЕТ СТАЦИОНАРНОЙ ТОЧКИ
kst1 = ((sk1^(1 - β1) * sh1^β1) / (n1 + δ1 + γ1))^(1 / (1 - α1 - β1))
hst1 = ((sk1^α1 * sh1^(1 - α1)) / (n1 + δ1 + γ1))^(1 / (1 - α1 - β1))
@show kst1 = round.(kst1, sigdigits=4);
@show hst1 = round.(hst1, sigdigits=4);
#решение системы дифференциальных уравнений (11)
function solouLid!(du, u, p, t)
α, β, sk, sh, n, δ, γ = p
du[1] = sk * u[1]^α * u[2]^β - (n + δ + γ) * u[1]
du[2] = sh * u[1]^α * u[2]^β - (n + δ + γ) * u[2]
end
u0 = [kA10, hA10]
p = (α1, β1, sk1, sh1, n1, δ1, γ1)
tspan = (0.0, 40.0)
probL = ODEProblem(solouLid!, u0, tspan, p)
solL = solve(probL, reltol=1e-8, abstol=1e-8)
# расчет y(t)
yA1 = zeros(length(solL[1, :]))
y1 = zeros(length(solL[1, :]))
yA1 = @.(solL[1, :]^α1 * solL[2, :]^β1)
At1 = @.exp(γ1 * solL.t) * A10
y1 = yA1 .* At1
#расчет N1(t)
N1 = zeros(length(solL[1, :]))
N1 = @.N10 * exp(solL.t[:, 1] * n1)
#расчет Y1(t)
Y1 = zeros(length(solL[1, :]))
Y1 = @.yA1 * At1 * N1;
# Модель Мэнкью – Ромера – Вейла : догоняющая страна
#ЗАДАНИЕ ИСХОДНЫХ ДАННЫХ
#начальная численность населения
@show N20 = 150;
#норма амортизации капитала
@show δ2 = 0.245;
#норма сбережения физического капитала
@show sk2 = 0.44;
#норма сбережения человеческого капитала
@show sh2 = 0.41;
# темп роста труда
@show n2 = 0.002;
#темп роста прогресса
@show γ2 = 0.030;
#эластичность выпуска по физическому капиталу
@show α2 = 0.40;
#эластичность выпуска по человеческому капиталу
@show β2 = 0.48;
#начальная капиталовооруженность по физическому капиталу
@show kA20 = 0.2;
#начальная капиталовооруженность по человеческому капиталу
@show hA20 = 0.25;
#начальное значение А
@show A20 = 2.0;
#РАСЧЕТ СТАЦИОНАРНОЙ ТОЧКИ
kst2 = ((sk2^(1 - β2) * sh2^β2) / (n2 + δ2 + γ2))^(1 / (1 - α2 - β2))
hst2 = ((sk2^α1 * sh2^(1 - α2)) / (n2 + δ2 + γ2))^(1 / (1 - α2 - β2))
@show kst2 = round.(kst2, sigdigits=4);
@show hst2 = round.(hst2, sigdigits=4);
#решение системы дифференциальных уравнений (11)
function solouDog!(du, u, p, t)
α, β, sk, sh, n, δ, γ = p
du[1] = sk * u[1]^α * u[2]^β - (n + δ + γ) * u[1]
du[2] = sh * u[1]^α * u[2]^β - (n + δ + γ) * u[2]
end
u0 = [kA20, hA20]
p = (α2, β2, sk2, sh2, n2, δ2, γ2)
tspan = (0.0, 40.0)
probD = ODEProblem(solouDog!, u0, tspan, p)
solD = solve(probD, reltol=1e-8, abstol=1e-8)
# расчет y2(t)
yA2 = zeros(length(solD[1, :]))
y2 = zeros(length(solD[1, :]))
yA2 = @.(solD[1, :]^α2 * solD[2, :]^β2)
At2 = @.exp(γ2 * solD.t) * A20
y2 = yA2 .* At2
#расчет N2(t)
N2 = zeros(length(solD[1, :]))
N2 = @.N20 * exp(solD.t[:, 1] * n2)
#расчет Y2(t)
Y2 = zeros(length(solD[1, :]))
Y2 = @.yA2 * At2 * N2
plotly()
theme(:dao)
p01 = plot(solL.t, y1, title="Доход на душу - США,Россия", label=("США"), lw=3, lc=:aqua)
plot!(solD.t, y2, label=("Россия"), lw=3, lc=:red)
p02 = plot(solL.t, Y1, title="Доход США,Россия", label="США", lw=3, lc=:blue)
plot!(solD.t, Y2, label="Россия", lw=3, lc=:red)
plot(p01, p02, layout=(1, 2), wsize=(1000, 250), xlabel="t", legend=:outertopright)
Выводы
В модели Мэнкью-Ромера-Вейла в базовую неоклассическую модель экономического роста Солоу вводится человеческий капитал, что улучшает теоретические положения модели. Эластичность выпуска по норме сбережений физического капитала равна единице при реалистических параметрах α = 1/3 (доля физического капитала в национальном продукте), и β = 1/3 (доля человеческого капитала), что больше соответствует эмпирическим данным, чем аналогичный результат модели Солоу без учета человеческого капитала. Темп прироста населения в данной модели также имеет большее значение и большее влияние на уровень дохода, чем в модели Солоу, что подтверждается эмпирическими оценками.
Однако основные результаты базовой неоклассической модели остаются без изменений, устойчивый экономический рост зависит от внешнего технического прогресса, в то же время норма сбережений, институциональные и поведенческие параметры на него не влияют. Следовательно, устойчивый экономический рост остается экзогенным по своему характеру.
Таким образом, хотя модель и является определённым шагом вперёд по сравнению с моделью Солоу, поскольку лучше описывает межстрановые различия, но при этом она не даёт объяснений причинам этих различий: по модели получается, что бедные страны бедны потому что им недостаёт физического или человеческого капитала, или потому что в них используются неэффективные технологии. Однако почему так происходит — модель не даёт ответа.