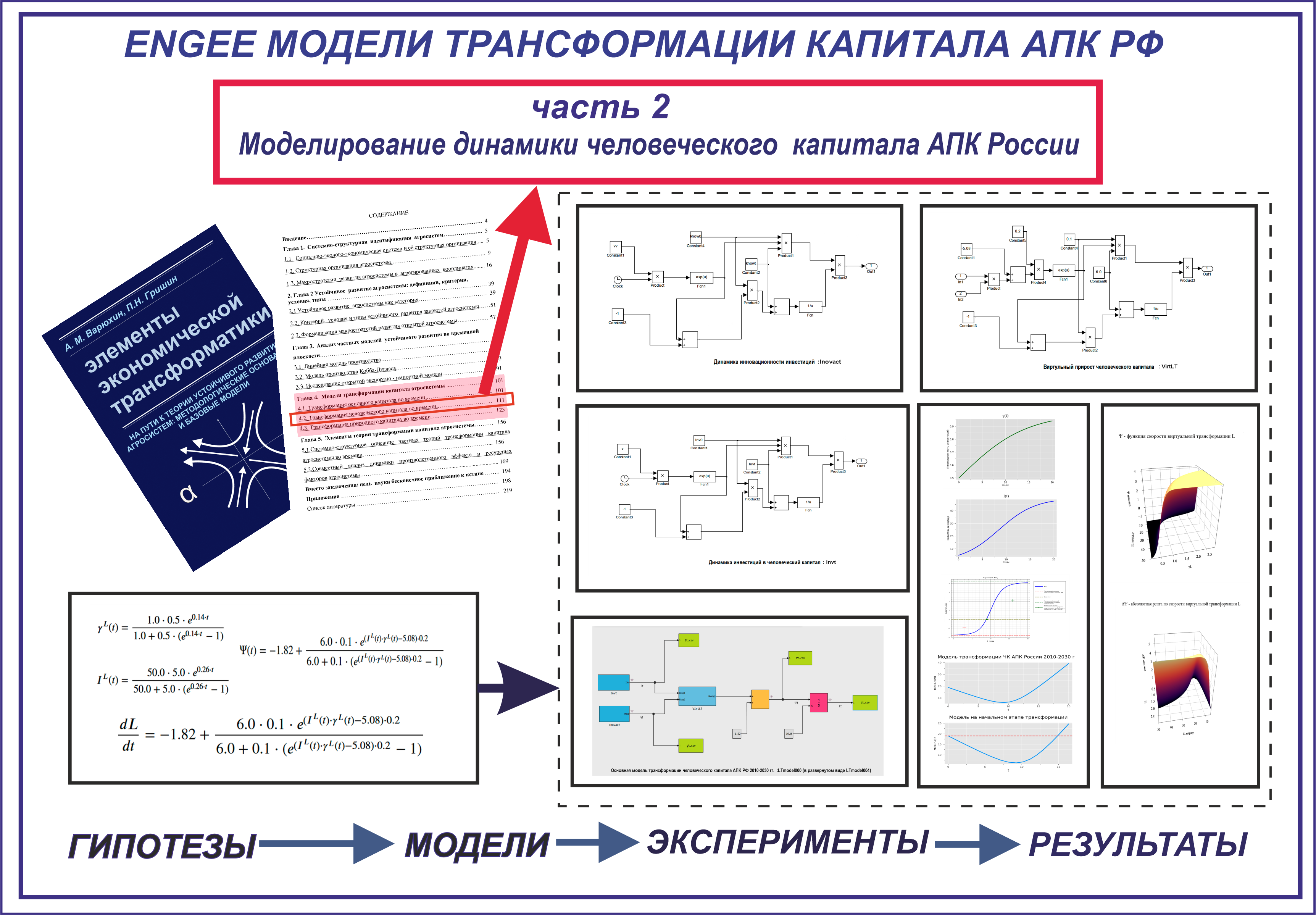
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДИНАМИКИ ЧЕЛОВЕЧЕСКОГО КАПИТАЛА АГРОСИСТЕМЫ РОССИИ И ЕЕ РЕАЛИЗАЦИЯ СРЕДСТВАМИ ENGEE.

Все теоретические результаты, используемые в этом проекте, взяты из монографии автора [1,глава 4, параграф 4.2]

Одной из важных компонент общего капитала аграрной социально-эколого-экономической системы (далее агросистема) является человеческий капитал, развитие которого в долговременной перспективе во многом определяет производственный потенциал аграрной сферы в целом. Это обуславливает большое практическое и теоретическое значение проблемы анализа динамики человеческого капитала на больших временных горизонтах в условиях необходимости перехода к новому технологическому укладу.

При анализе человеческого капитала агросистемы России необходимо рассматривать: численность сельского населения, его половозрастную структуру, уровень здоровья и образования, вовлеченность в аграрные процессы. Учитывая основные тенденции развития человеческого капитала агросистемы России, и формулируя определенные гипотезы относительно его долговременной динамики, попытаемся построить соответствующую динамическую математическую модель.

Представим процесс движения человеческого капитала в дискретном времени следующим уравнением:

где
-человеческий капитал соответственно в моменты ;

;

-численность населения в момент ;

;

-прирост (убыль) численности населения;

- коэффициент трансформации населения в человеческий капитал;

- виртуальный прирост (убыль) человеческого капитала за счет совершенствования (ухудшения) его структуры и качества ;

$\Delta \mathop L\nolimits_t^C = \mathop \chi \nolimits_t^{CL} \mathop L\nolimits_t $ -- катастрофическое уменьшение человеческого потенциала

( коэффициент катастрофических потерь человеческого капитала).
Тогда имеем коэффициент трансформации человеческого капитала во времени:

или

где

- индекс, характеризующий естественный рост (убыль) населения;

-индекс, характеризующий динамику коэффициента трансформации численности населения в человеческий капитал;

-инвестиции в развитие структуры и качества человеческого капитала;

- функция трансформации инвестиций, с учетом их инновационности, в виртуальный прирост (снижение) человеческого капитала;

- коэффициент, характеризующий уровень инновационности использования инвестиций в развитие человеческого капитала.
Коэффициент интегрально характеризует структурное и качественное развитие человеческого потенциала агросистемы.Именно через коэффициент находят свое количественное выражение уровень цивилизованности человеческих ресурсов, определяющий магистральное направление в их развитии (виртуализацию ресурсов). Временные траектории движения данного коэффициента, во многом, определяют типологию развития человеческого потенциала

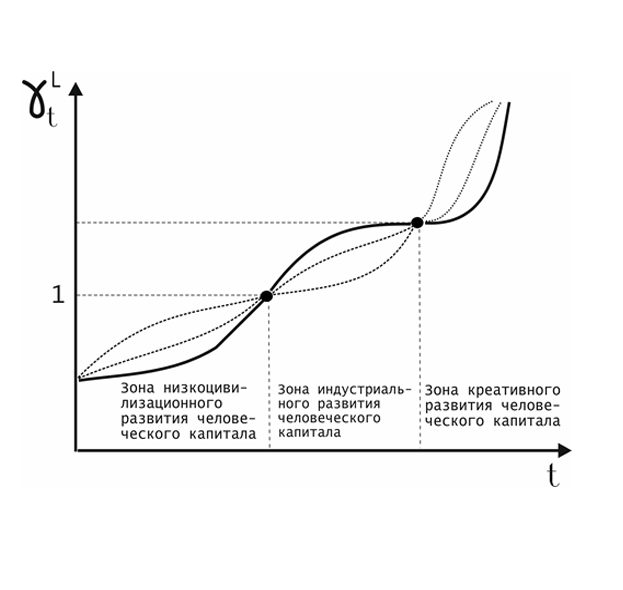
Из выражения ( 3 ) видно, что развитие человеческого капитала определяется демографическими процессами, формирующими естественный прирост населения (), социально политическими и экономическими процессами, детерминирующими уровень вовлеченности населения в производительную деятельность (), достигнутым уровнем развития человеческого потенциала (), уровнем инвестиций в человеческий потенциал () и уровнем инновационности использования инвестиций в развитие человеческого капитала () и возникновением катастрофических событий ().

Основное дискретное динамическое соотношение:

Перейдем от дискретного к не прерывному времени. Вычитая из обеих частей уравнения (4) получим следующее уравнение:

Переходя к бесконечно малым приращениям, получаем следующее дифференциальное уравнение:

Получим удельное динамическое уравнение для человеческого капитала в дискретном времени:

где и человеческий капитал на душу населения соответственно в и периоды времени.

Тогда

и переходя к малым приращениям, получаем удельное дифференциальное уравнение:

Где -инвестиции в человеческий капитал АСЭЭС на душу населения в период , а

Введем функцию, описывающую зависимость виртуального приращения человеческого капитала на душу населения, от инвестиций на душу населения и их инновационности .

Тогда имеем следующее дифференциальное уравнение:

Исследуем правую часть уравнения (7). Имеем функцию:

Она описывает естественную динамику человеческого капитала аграрной сферы, которая определяется следующими процессами: демографической динамикой населения , динамикой вовлечения населения в профессиональную деятельность в аграрном секторе экономики и возможностью возникновения с определенной вероятностью крупных природных или социальных катаклизмов, приводящих к физической убыли значительной части населения .
Для России можно достаточно уверенно прогнозировать на 20 лет (принимаем и ). Кроме того, будем считать, что значительных катаклизмов не произойдет , следовательно, . То есть, в уравнении (7) ей можно пренебречь. Таким образом, естественных условий для роста человеческого капитала в аграрной сфере России на ближайшие 20 лет нет.

Рассмотрим функцию , которая описывает скорость трансформации инвестиций в развитие человеческого капитала агросферы в его виртуальный прирост (падение) за счет повышения (понижения) качества и совершенствования (ухудшения) структуры. Конструирование подобной функции это один из возможных способов количественно измерить качество и структуру человеческого капитала.

Данная функция конструируется из следующих экономических соображений:

существует диапазон инвестиций где при ,что экономически означает быстрое разрушение человеческого потенциа-ла, когда инвестиции в его развитие ниже некоторого предельного уровня ( - предельно допустимое падение человеческого капитала на уровне инновационности инвестиций );
в диапазоне при , где - предельный верхний уровень виртуального роста человеческого капитал при господствующем типе его воспроизводства и уровне его инновационности , при приближении к которому скорость виртуального прироста человеческого капитала стремиться к нулю (закон уменьшающейся отдачи от вложений);
в диапазоне существует точка , где функция трансформации ,то есть при заданном уровне инновационности инвестиций существует общественно необходимый их уровень, при котором обеспечивается режим сохранения естественного воспроизводства человеческого капитала и экономика работает без дополнительных потерь и приобретений. При - аграрная сфера экономики несет потери, а при приобретает дополнительный человеческий капитал;
при и разность значений функций задает абсолютную инновационную латентную ренту по скорости виртуальной трансформации человеческого капитала , если ввести величину ,то имеем относительную латентную ренту:

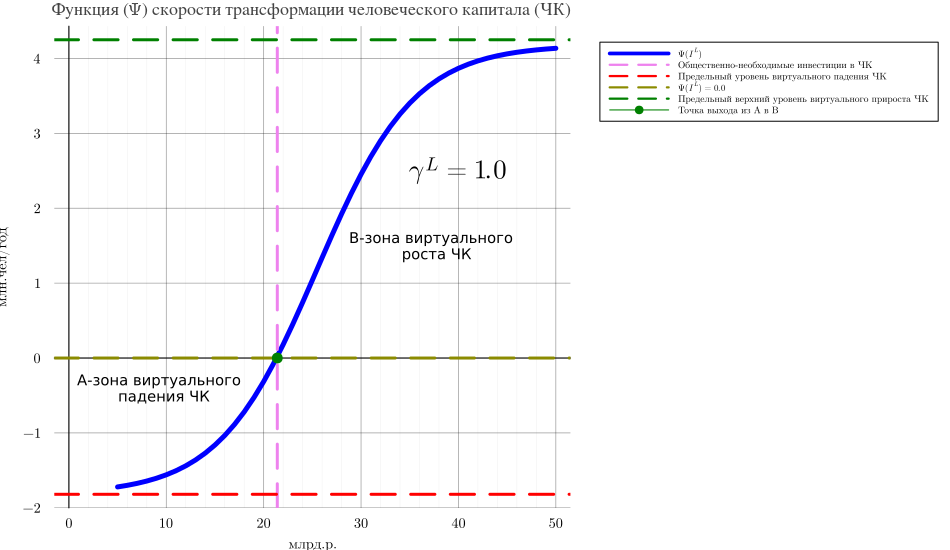
Ренты мы назвали латентными, так как они открыто проявляются лишь через дополнительный продукт аграрного производства, полученный благодаря более высокому качеству человеческого капитала.Для иллюстрации представим функцию скорости трансформации человеческого капитала, удовлетворяющую сформулированным выше требованиям при .

using RDatasets, Plots, PlotThemes
using DataFrames
using LaTeXStrings

# γ^L=1.0 инновационность инвестиций на среднем уровне передовых стран   
IL = 5:50 #прямые инвестиции в человеческий капитал 5-50 млрд. р 

Psi = @.( (6.0 * 0.1 * exp(0.2 * (IL - 5.08))) / (6.0 + 0.1 * (exp(0.2 * (IL - 5.08)) - 1)) - 1.82)
gr()
#plotly()
theme(:dao)

default(titlefont=(11, "times"),legendfontsize=6, guidefont=(9, :black), tickfont=(9, :black), guide="x", framestyle=:zerolines, yminorgrid=false)
plot(IL, Psi, lw=5, title="Функция (Ψ) скорости трансформации человеческого капитала (ЧК)", xlabel="млрд.р.", 
ylabel="млн.чел/год", lc=:blue, wsize=(950, 550), label=L"Ψ(I^L)")
vline!([21.4], lw=3, lc=:violet, linestyle=:dash, label="Общественно-необходимые инвестиции в ЧК")
hline!([-1.82], lw=3, lc=:red, linestyle=:dash, label="Предельный уровень виртуального падения ЧК")
hline!([0.0], lw=3, lc=:yellow4, linestyle=:dash, label=L"Ψ(I^L)=0.0")
hline!([4.25], lw=3, lc=:green, linestyle=:dash, label="Предельный верхний уровень виртуального прироста ЧК")
annotate!([9.5], [-0.4], [text("А-зона виртуального \n падения ЧК", 10)])
annotate!([37.5], [1.5], [text("B-зона виртуального \n роста ЧК", 10)])
annotate!([40.0], [2.5], [text(L"γ^L=1.0", 18)])
plot!([21.4], [0.0], label="Точка выхода из А в В",
    seriescolor=:green,
    marker=:circle,
    markersize=6,
    markercolor=:green,
    markerstrokecolor=:green
)

Здесь прямые инвестиции в повышение качества человеческого капитала АСЭЭС находятся в интервале от 5 млрд. рублей (предельно-допустимый нижний уровень инвестиций) до 50 млрд. рублей. Предельная скорость виртуального падения человеческого капитала составляет 1,82 млн. чел (около 1 процента экономически активного сельского населения России). Общественно-необходимые инвестиции определены на уровне 22 млрд. рублей, предельный верхний уровень скорости виртуального прироста человеческого капитала порядка 4,1 млн.чел (2,1 процент экономически активного сельского населения России). Уровень инновационности использования инвестиций принят равным единице. Параметры функции могут быть определены из анализа развития человеческого капитала агросферы экономически передовых стран.
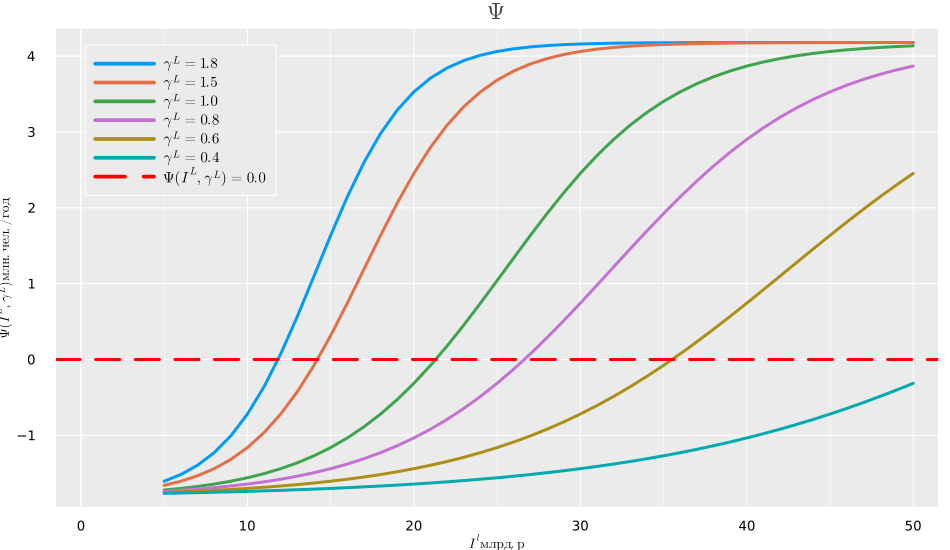
Функция скорости трансформации при различных уровнях инновационности использования инвестиций в человеческий потенциал АСЭЭС может быть представлена следующим образом (см.ниже)

using Plots, PlotThemes
using LaTeXStrings

INV = 5.0:50.0
GammaL = [1.8, 1.5, 1.0, 0.8, 0.6, 0.4]
Met=[L"γ^L=1.8",L"γ^L=1.5",L"γ^L=1.0",L"γ^L=0.8",L"γ^L=0.6",L"γ^L=0.4"]

gr()
#plotly()
theme(:ggplot2)

default(titlefont=(14, "times"), legendfontsize=10, guidefont=(9, :black), tickfont=(9, :black), guide="x", framestyle=:zerolines, yminorgrid=false)

plot(wsize=(950, 550))
for i in 1:6
    Ψi = @.((6.0*0.1*exp(0.2*(GammaL[i]*INV-5.08)))/(6.0+0.1*(exp(0.2*(GammaL[i]*INV-5.08))-1))-1.82)
    plot!(INV, Ψi, label=Met[i], lw=3)
end
plot!(title="Ψ", xlabel=L"I^l млрд.р", ylabel=L"Ψ(I^L,γ^L) млн.чел./год")
hline!([0.0], lw=3, lc=:red, linestyle=:dash, label=L"Ψ(I^L,γ^L)=0.0")

Из графика видно, что, чем ниже уровень инновационности и эффективности использования инвестиций в человеческий капитал, тем больше требуется средств для обеспечения необходимого режима его воспроизводства.
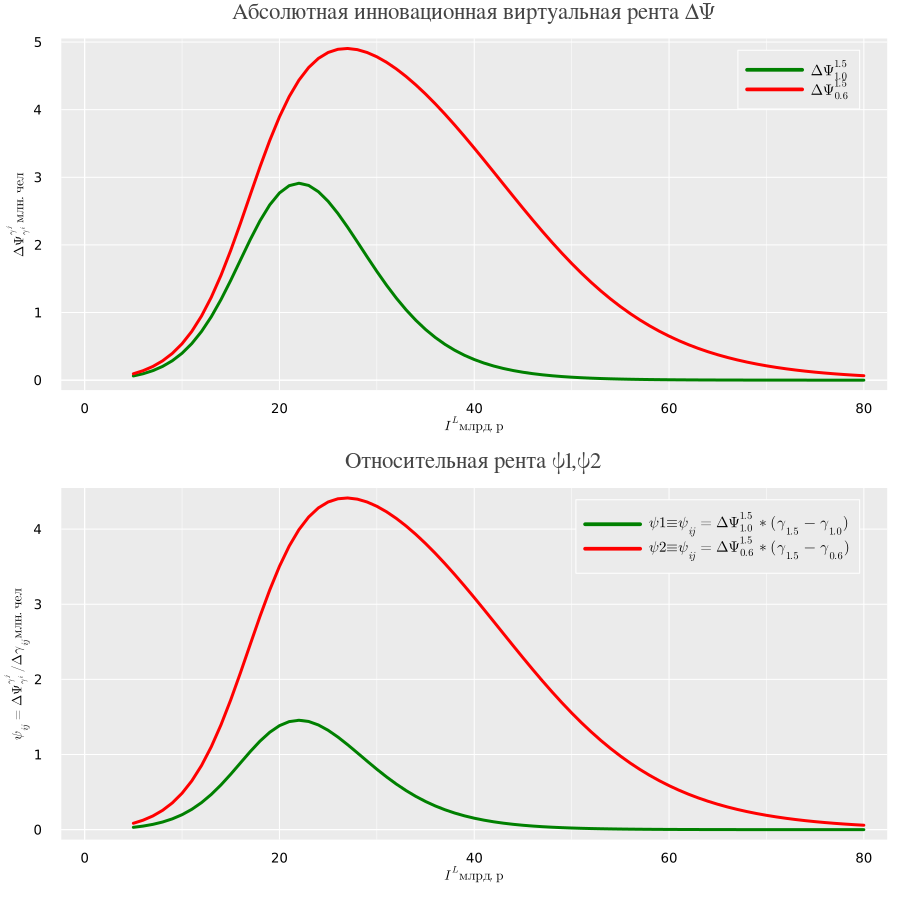
Рассмотрим, как изменяется введенная выше латентная абсолютная и относительная рента по скорости виртуальной трансформации человеческого капитала АСЭЭС в пространстве инвестиций (см.ниже)

using Plots, PlotThemes
using LaTeXStrings

INV = 5.0:80.0
GammaL = [1.5, 1.0, 1.5, 0.6]


Ψ0 =@.((6.0*0.1*exp(0.2*(GammaL[1]*INV-5.08)))/(6.0+0.1*(exp(0.2*(GammaL[1]*INV-5.08))-1))-1.82)
Ψ1 =@.((6.0*0.1*exp(0.2*(GammaL[2]*INV-5.08)))/(6.0+0.1*(exp(0.2*(GammaL[2]*INV-5.08))-1))-1.82)
Ψ2 =@.((6.0*0.1*exp(0.2*(GammaL[3]*INV-5.08)))/(6.0+0.1*(exp(0.2*(GammaL[3]*INV-5.08))-1))-1.82)
Ψ3 =@.((6.0*0.1*exp(0.2*(GammaL[4]*INV-5.08)))/(6.0+0.1*(exp(0.2*(GammaL[4]*INV-5.08))-1))-1.82)
ΔΨ1 = @.(Ψ0 - Ψ1)
ΔΨ2 = @.(Ψ2 - Ψ3)

gr()
#plotly()
theme(:ggplot2)

default(titlefont=(14, "times"), legendfontsize=10, guidefont=(9, :black), tickfont=(9, :black), guide="x", framestyle=:zerolines, yminorgrid=false)

p1=plot(INV, ΔΨ1, title="Абсолютная инновационная виртуальная рента ΔΨ", xlabel=L"I^L млрд.р", ylabel=L"ΔΨ^{γ^j}_{γ^i} млн.чел",
   label=L"ΔΨ^{1.5}_{1.0}", lw=3, lc=:green)
plot!(INV, ΔΨ2, label=L"ΔΨ^{1.5}_{0.6}", lw=3, lc=:red)

Δγ1 = 1/(GammaL[1]-GammaL[2])
Δγ2 = 1/(GammaL[3]-GammaL[4])
ψ1 = @.(ΔΨ1/Δγ1)
ψ2 = @.(ΔΨ2/Δγ2)
Δγ1 = 1 / (GammaL[1] - GammaL[2])
Δγ1 = 1 / (GammaL[1] - GammaL[2])

p2 = plot(INV, ψ1, title="Относительная рента ψ1,ψ2", xlabel=L"I^L млрд.р", ylabel=L"ψ_{ij}=ΔΨ^{γ^j}_{γ^i}/Δγ_{ij} млн.чел", 
   label=L"ψ1≡ψ_{ij}=ΔΨ^{1.5}_{1.0}*(γ_{1.5}-γ_{1.0})", lw=3, lc=:green)
plot!(INV, ψ2, label=L"ψ2≡ψ_{ij}=ΔΨ^{1.5}_{0.6}*(γ_{1.5}-γ_{0.6})", lw=3, lc=:red)

plot(p1, p2 , layout=(2, 1), wsize=(900, 900))

Из графиков отчетливо видно, что в пространстве инвестиций латентная рента по скорости виртуальной трансформации человеческого капитала представляет собой дифференцируемую, непрерывную функцию определенную на интервале от пяти до плюс бесконечности,которая имеет максимум и асимптоту равную нулю,то есть можно определить величину инвестиций, превышение которых приводит к снижению латентной абсолютной и относительной ренты по скорости виртуальной трансформации L.
Трехмерный график функции трансформации пространстве инноваций и инвестиций имеет следующий вид (см. ниже)

#ГРАФИК ФУКЦИИ СКОРОСТИ ТРАНСФОРМАЦИИ ЧЕЛОВЕЧЕСКОГО КАПИТАЛА В ПРОСТРАНСТВЕ ИНВЕСТИЦИЙ И ИННОВАЦИЙ
using Plots, PlotThemes
using LaTeXStrings

INV = (5.0:0.5:50.0)
γ = (0.1:0.1:2.9)

Ψ(INV,γ) = -1.82 + 6 * 0.1 * exp((γ * INV - 5.08) * 0.2) / (6 + 0.1 * (exp((γ * INV - 5.08) * 0.2) - 1))

#gr()
plotly()
theme(:dao)
default(titlefont=(14, "times"), legendfontsize=10, guidefont=(9, :black), tickfont=(9, :black))
surface(INV, γ, Ψ, linewidth=3, xlabel="IL млрд.р",ylabel="γL",zlabel="Ψ млн.чел", wsize=(900, 600),legend=false)
title!("Ψ - функция скорости виртуальной трансформации L")

#График абсолютной ренты по скорости виртуальной трансформации L в пространстве инвестиций и инноваций.
#значение показателя инновационномти берется как разность предельного(принимается =3) и текущего значения из (0.0,3.0)  
using Plots, PlotThemes
using LaTeXStrings

INV = (5.0:0.5:50.0)
Y = (0.1:0.1:2.9)

R11(INV) = -1.82 + 6 * 0.1 * exp((3.0 * INV - 5.08) * 0.2) / (6 + 0.1 * (exp((3.0 * INV - 5.08) * 0.2) - 1))
R33(INV,Y) = -1.82 + 6 * 0.1 * exp(((3.0 - Y) * INV - 5.08) * 0.2) / (6 + 0.1 * (exp(((3.0 - Y) * INV - 5.08) * 0.2) - 1))
ΔΨ(INV, Y) = R11(INV) - R33(INV, Y)

plotly()
theme(:dao)
default(titlefont=(14, "times"), legendfontsize=10, guidefont=(9, :black), tickfont=(9, :black))
surface(INV, Y, ΔΨ, linewidth=3, xlabel="IL млрд.р",ylabel="γL",zlabel="ΔΨ млн.чел", wsize=(900, 600),legend=false)
title!("ΔΨ - абсолютная рента по скорости виртуальной трансформации L")

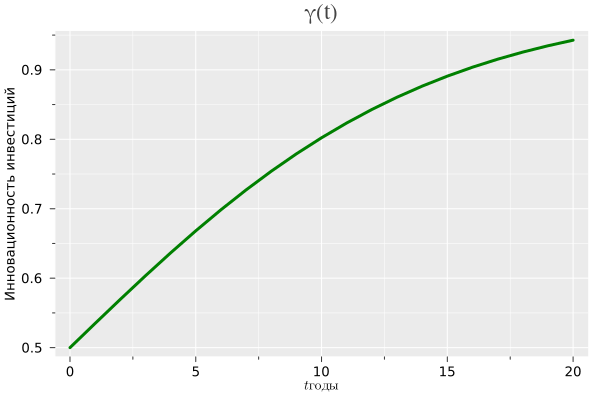
Исследуем функцию во временной плоскости. Зададим динамику инновационности инвестиций в человеческий капитал в виде следующей логистической функции:

Графически она имеет следующий вид (смотри ниже)

using Plots, PlotThemes
using LaTeXStrings

t = 0:20 #временной интервал исследования
γt =@.((1.0 * 0.5 * exp(0.14 * t)) / (1.0 + 0.5 * (exp(0.14 * t) - 1)))

gr()
#plotly()
theme(:ggplot2)

default(titlefont=(14, "times"), legendfontsize=10, guidefont=(9, :black), tickfont=(9, :black))

plot(t, γt, title="γ(t)", xlabel=L"t годы", ylabel="Инновационность инвестиций",  label=false, lw=3, lc=:green)

Экономический смысл этой функции следующий. В момент уровень инновационности и эффективности инвестиций в человеческий капитал АСЭЭС России ,то есть, составляет 40-50 процентов от общественно-необходимого уровня, за который принимается средний уровень наиболее развитых в аграрном отношении стран. К 2030-2031 году предполагается достигнуть общественно необходимого уровня инновационности.
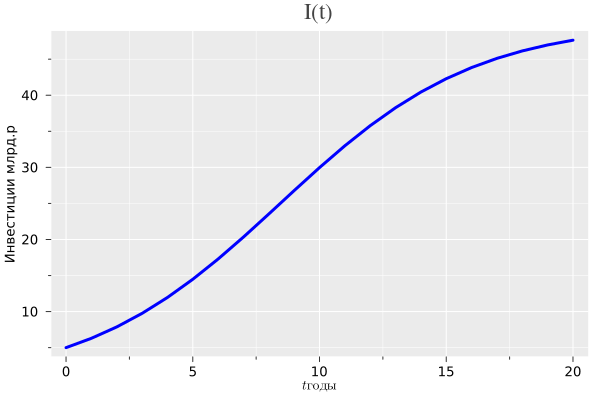
Динамику инвестиций зададим следующей функцией:

using Plots, PlotThemes
using LaTeXStrings

t = 0:20 #временной интервал исследования
It =@.((50.0 * 5.0 * exp(0.26 * t)) / (50.0 + 5.0 * (exp(0.26 * t) - 1)))

gr()
#plotly()
theme(:ggplot2)

default(titlefont=(14, "times"), legendfontsize=10, guidefont=(9, :black), tickfont=(9, :black))
plot(t, It, title="I(t)", xlabel=L"t годы", ylabel="Инвестиции млрд.р", label=false, lw=3, lc=:blue)

Эта функция задает на 20 лет простой инвестиционный сценарий в области развития человеческого капитала АСЭЭС России, предполагающий рост прямых инвестиций в этой сфере с 5 млрд. рублей до 45-50 млрд. рублей (естественно, что инвестиции приведены к начальному периоду).
Тогда функция скорости виртуального прироста человеческого капитала в агросфере России будет иметь вид:

Графически эта функция будет иметь следующий вид (смотри ниже)

using Plots, PlotThemes
using LaTeXStrings

t = (0.0:0.5:20.0) #временной интервал исследования

γt = @.((1.0 * 0.5 * exp(0.14 * t)) / (1.0 + 0.5 * (exp(0.14 * t) - 1)))
It = @.((50.0 * 5.0 * exp(0.26 * t)) / (50.0 + 5.0 * (exp(0.26 * t) - 1)))
Ψt = @.(-1.82 + ((6.0 * 0.1 * exp((It * γt - 5.08) * 0.2)) / (6.0 + 0.1 * (exp((It * γt - 5.08) * 0.2)) - 1)))

gr()
#plotly()
theme(:dao)


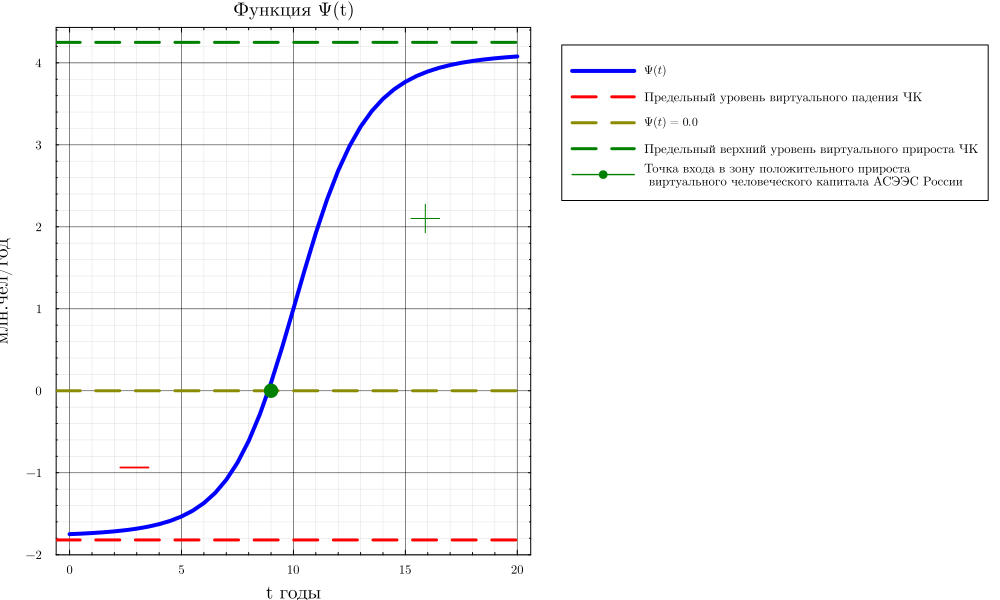
plot(t, Ψt, lw=4, title="Функция Ψ(t)", xlabel="t годы",ylabel="млн.чел/год", lc=:blue, wsize=(1000, 600), label=L"Ψ(t)")
hline!([-1.82], lw=3, lc=:red, linestyle=:dash, label="Предельный уровень виртуального падения ЧК")
hline!([0.0], lw=3, lc=:yellow4, linestyle=:dash, label=L"Ψ(t)=0.0")
hline!([4.25], lw=3, lc=:green, linestyle=:dash, label="Предельный верхний уровень виртуального прироста ЧК")
annotate!([16.0], [2.1], [text(L"+",:green, 30)])
annotate!([3.0], [-1.0], [text(L"-",:red,30)])
plot!([9.0], [0.0], label="Точка входа в зону положительного прироста\n виртуального человеческого капитала АСЭЭС России",
    seriescolor=:green,
    marker=:circle,
    markersize=8,
    markercolor=:green,
    markerstrokecolor=:green
)

Из графика видно, что при предлагаемых выше сценарных условиях виртуальный прирост человеческого капитала АСЭЭС России первые 9 лет будет находиться в отрицательной зоне. То есть, это означает, что в связи с низким качеством человеческого капитала и недостаточными инвестициями в его развитие, низким уровнем их инновационности первые 9 лет из эффективного аграрного производства будет выпадать в среднем ежегодно до 194 тыс. чел. В дальнейшем с ростом инвестиций и их инновационности можно ожидать рост скорости виртуального прироста человеческого капитала в конце сценарного срока на уровне 4 млн.человек в год.

Учитывая выше введенные соотношения, имеем следующее дифференциальное уравнение, описывающее динамику человеческого капитала АСЭЭС:

Численное решение этого уравнения при (численность экономически активного сельского населения России в 2010 году) имеет следующий вид (смотри ниже):

#=Модель трансформации человеческого капитала АПК=#
using DifferentialEquations, Plots, PlotThemes
#a = 50.0
#b = 5.0
#c= 1.0
#d = 0.5
#p = (50.0, 5.0,1.0, 0.5)

function fL(u, p, t)
    n11 = (50.0 * 5.0 * exp(0.26 * t)) / (50.0 + 5.0 * (exp(0.26 * t) - 1.0))
    n12 = (1.0 * 0.5 * exp(0.14 * t)) / (1.0 + 0.5 * (exp(0.14 * t) - 1.0))
    n1 = exp((n11 * n12 - 5.08) * 0.2)
    du = -1.82 + ((6.0 * 0.1 * n1) / (6.0 + 0.1 * (n1 - 1.0)))
    [du]
end

tspan = (0.0, 20.0)
u0 = [19.0]

prob = ODEProblem(fL, u0, tspan)
sol = solve(prob, abstol=1e-8, reltol=1e-8)

T1 = deepcopy(sol.t)
F1 = deepcopy(sol.u)
F1 = reduce(vcat, F1);

theme(:ggplot2)

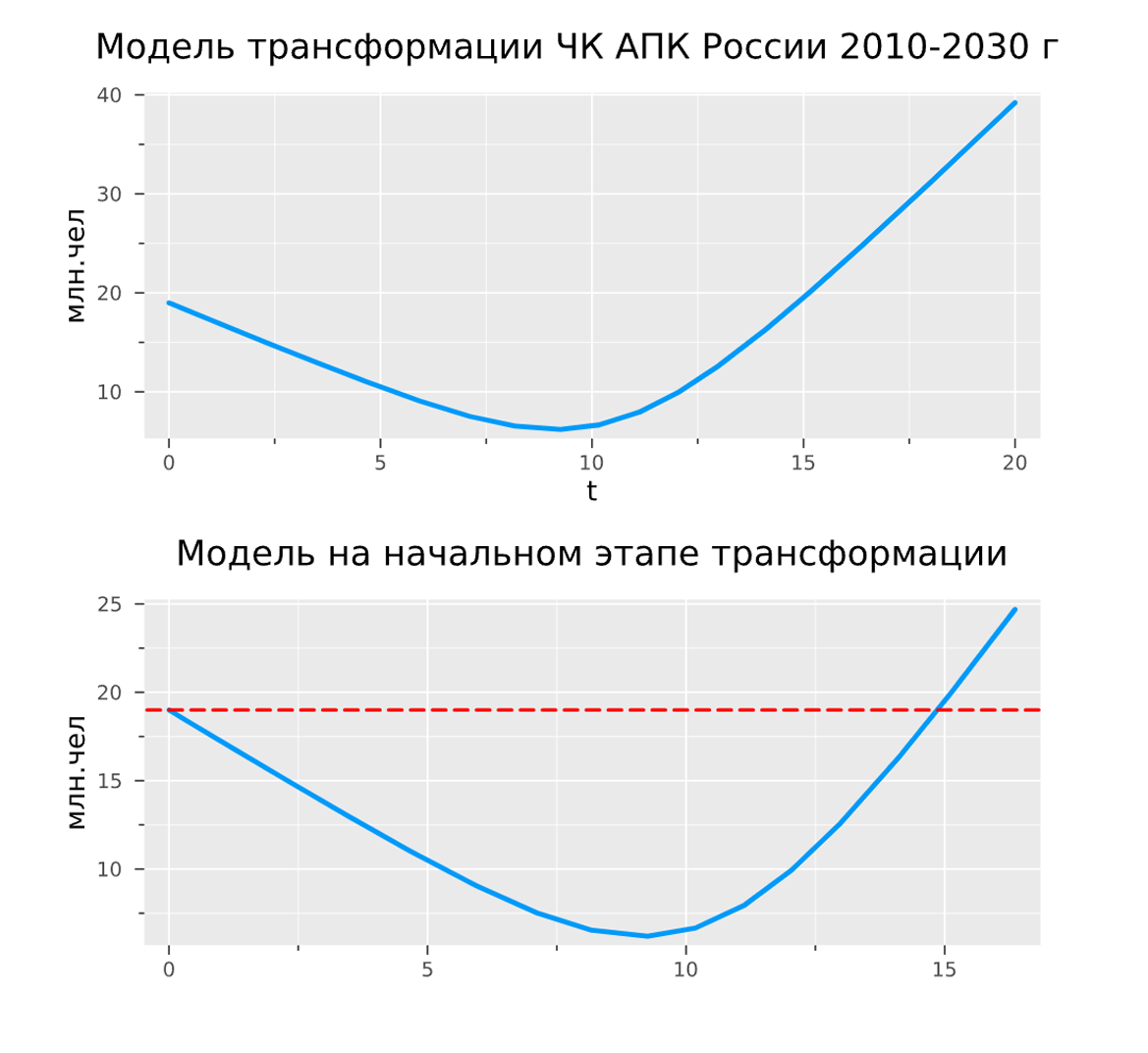
p5 = plot(T1, F1, title="Модель трансформации ЧК АПК России 2010-2030 гг.", ylabel="млн.чел", xlabel="t", lw=3)
p6 = plot(T1[1:18], F1[1:18], title="Модель на начальном этапе трансформации", ylabel="млн.чел", xlabel="t", lw=3)
hline!([19.0], lw=2, lc=:red, linestyle=:dash)
plot(p5, p6, layout=(2, 1), wsize=(800, 900), legend=false)

Решим уравнение (16) средствами визуального моделирования Engee при начальных условиях L(0) = 19.0 на интервале t=[0.0,20.0]. Engee-модель «LTmodel000», решающая данное уравнение имеет следующий вид :

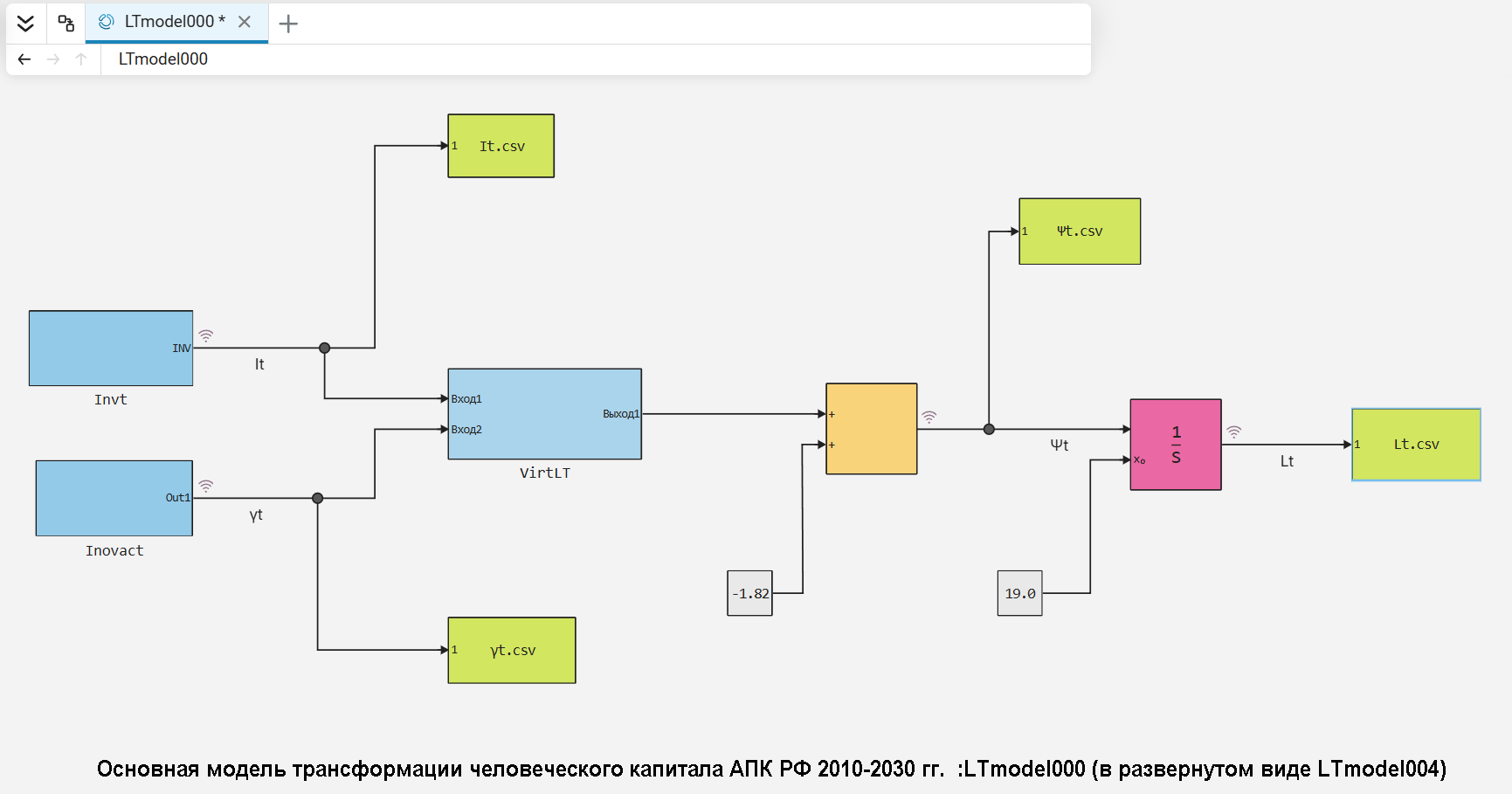
В этой Engee-модели используются три подмодели «invt», «inovact» и «VirtLT». Подмодель «invt» описывает динамику инвестиций в человеческий капитал. Она имеет следующий вид :

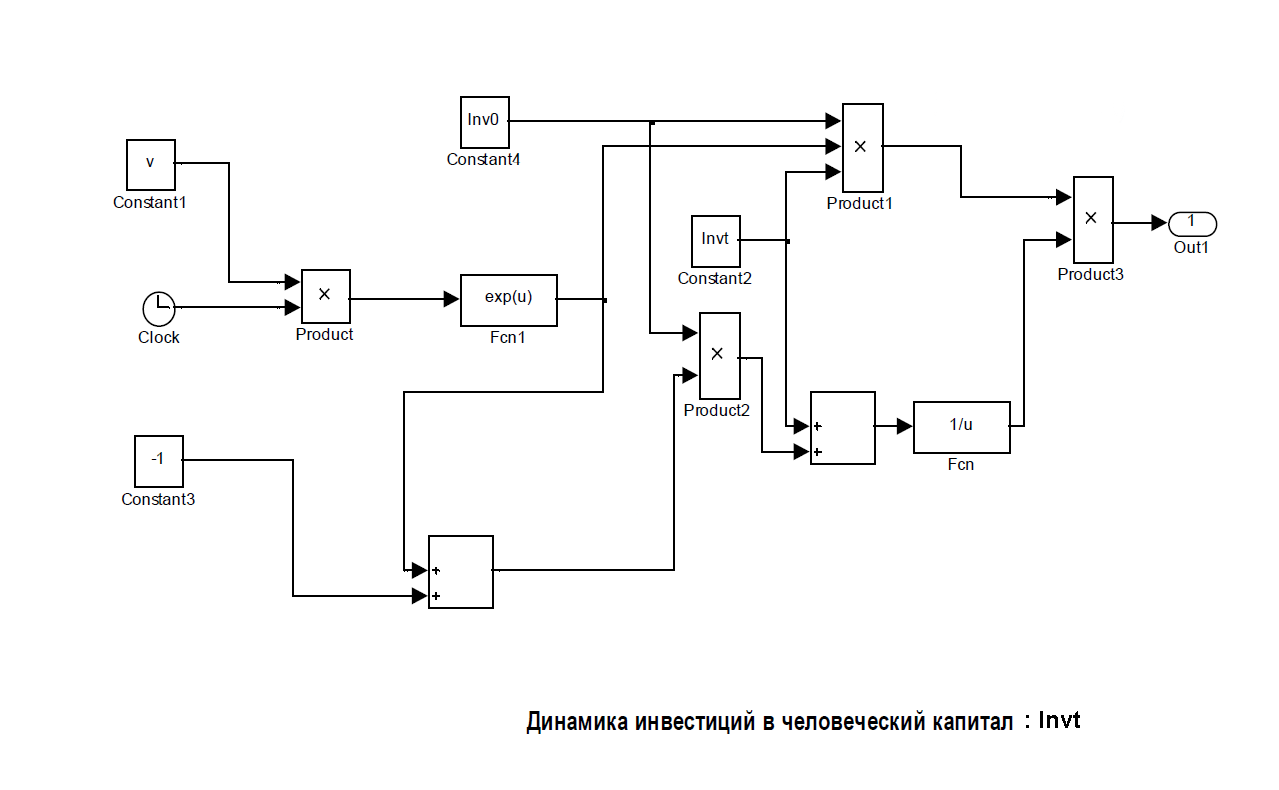
Подмодель «inovact» описывает динамику инновационности инвестиций в человеческий капитал. Она имеет следующий вид :

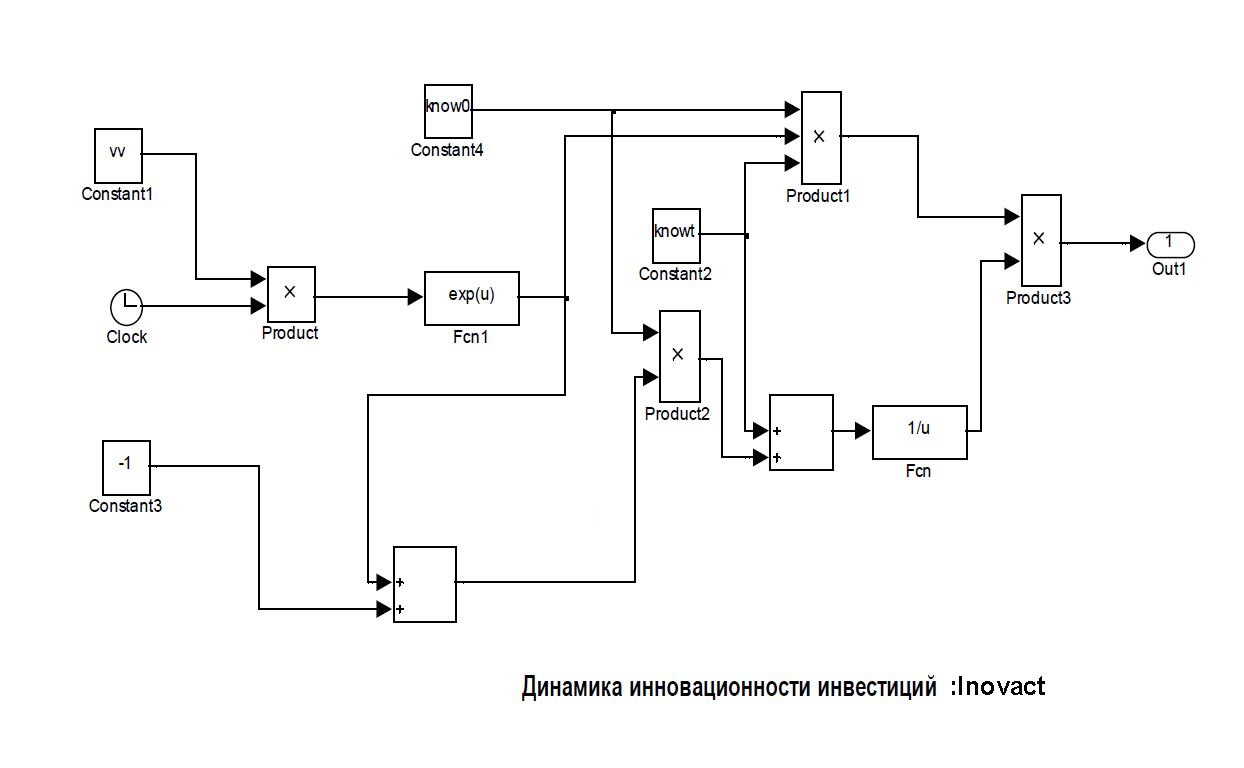
Подмодель «VirtLT» описывает функцию Ψ(t) + 1.82 виртуального прироста человеческого капитала в агросфере. Она имеет следующий вид :

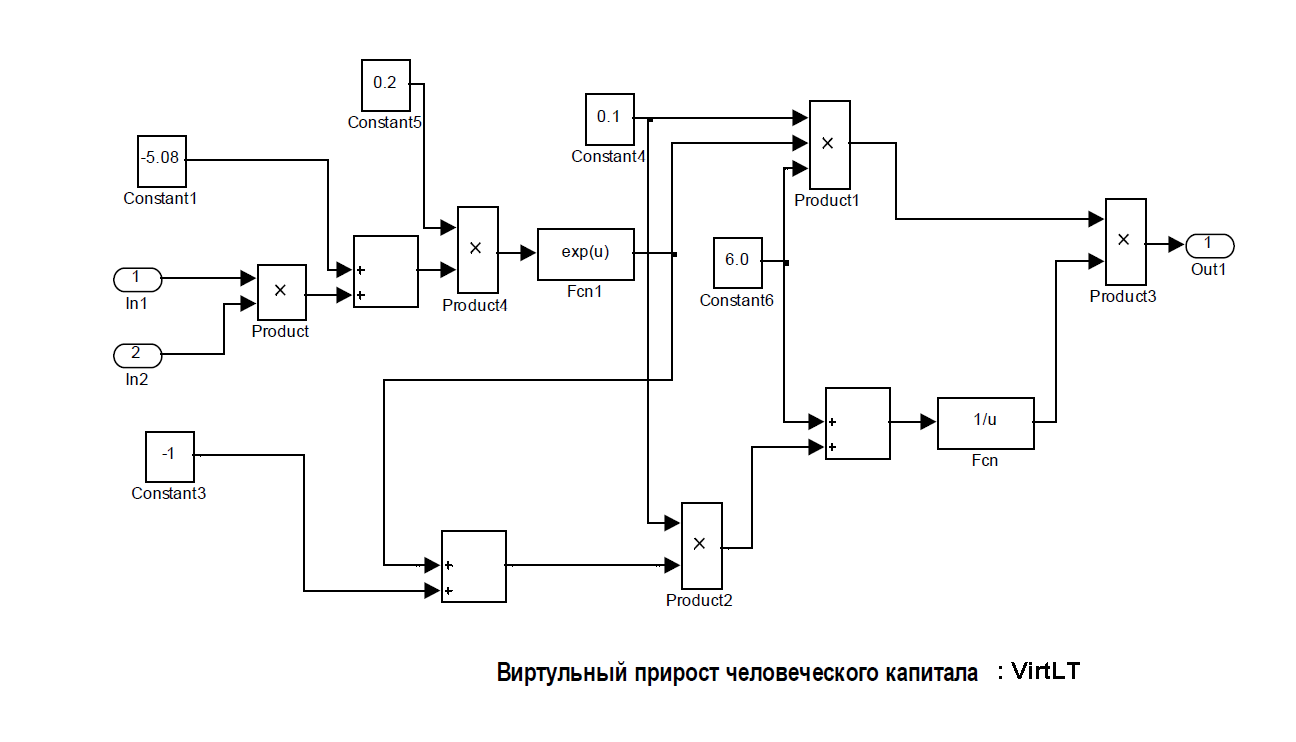
Для исследования с помощью этих моделей динамики человеческого капитала агросистемы России мы разработали соответствующий julia скрипт, в результате его работы мы получили графические результаты, которые представлены ниже.

#ИССЛЕДОВАНИЕ ДИНАМИКИ ЧЕЛОВЕЧЕСКОГО КАПИТАЛА В ENGEE
using RDatasets, Plots, PlotThemes
using CSV, DataFrames, LaTeXStrings


#открытие модели
modelName = "LTmodel004";
PID_model = modelName in [m.name for m in engee.get_all_models()] ? engee.open(modelName) :
            engee.load("/user/ModTL/$(modelName).engee");
engee.set_param!(modelName, "StopTime" => 20.0) # задание интервала моделирования

#параметры модели
#Начальный уровень инвестиций
global rub0=5.0;
#Целевой уровень инвестиций
global rubt = 50.0;
#Параметр регулирующий скорость роста инвестиций
global v = 0.26;
#Начальный уровень инновационности инвестиций
global know0 = 0.5;
#Целевой уровень инновационности инвестиций
global knowt = 1.0;
#Параметр регулирующий скорость роста инновационности инвестиций
global vv = 0.14;

engee.run(modelName) #запуск модели

It = CSV.read("/user/It.csv", DataFrame)
γt = CSV.read("/user/γt.csv", DataFrame)
Ψt = CSV.read("/user/Ψt.csv", DataFrame)
Lt = CSV.read("/user/Lt.csv", DataFrame)

gr()
#plotly()
theme(:dao)

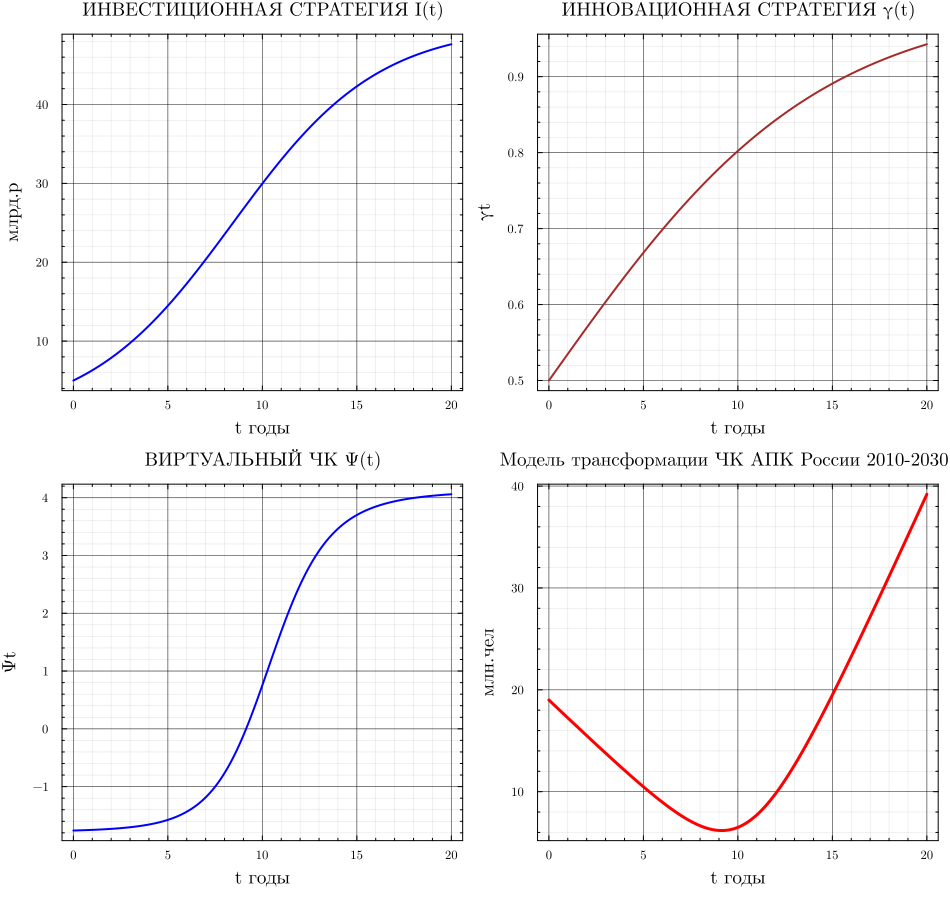
p1= plot(It[!, "time"], It[!, "It"], lw=2, title="ИНВЕСТИЦИОННАЯ СТРАТЕГИЯ I(t)", xlabel="t годы", ylabel="млрд.р", lc=:blue)
p2= plot(γt[!, "time"], γt[!, "γt"], lw=2, title="ИННОВАЦИОННАЯ СТРАТЕГИЯ γ(t)", xlabel="t годы", ylabel="γt", lc=:brown)
p3= plot(Ψt[!, "time"], Ψt[!, "Ψt"], lw=2, title="ВИРТУАЛЬНЫЙ ЧК Ψ(t)", xlabel="t годы", ylabel="Ψt", lc=:blue)
p4= plot(Lt[!, "time"], Lt[!, "Lt"], title="Модель трансформации ЧК АПК России 2010-2030 гг.",ylabel="млн.чел", xlabel="t годы",lc=:red, lw=3)
plot(p1, p2,p3,p4, layout=(2, 2), wsize=(950, 900), legend=false)

Если проанализировать полученное решение, то можно сделать следующие выводы. Согласно сформулированным выше предположениям, фактическая численность работающих в аграрном секторе России есть величина практически неизменная и равная приблизительно 19 млн. человек. Поэтому динамика полностью определяется виртуальной составляющей человеческого капитала.
В сценарном периоде выделяется три различных подпериода. Первый длится 9 лет. Здесь, в связи с низким качеством человеческого капитала и недостаточными инвестициями в его развитие, низким уровнем их инновационности происходит падение совокупного человеческого капитала с 19 млн. человек до 6.2 млн. человек. Это означает, что фактически работающие в аграрной сфере России 19 млн. человек дают такие же результаты, как в среднем 6.3 млн. человек в аграрно-развитых странах мира.
Второй подпериод, с 9 по 15 годы, характеризуется началом роста совокупного человеческого капитала за счет виртуальной составляющей. К 15 году достигается равенство совокупного и фактического человеческого потенциала, что означает, что весь фактический человеческий потенциал достиг общественно-необходимого уровня. На третьем этапе, с 15 по 20 год, идет быстрый рост совокупного человеческого потенциала за счет более высокого, чем в среднем по развитым странам, качества человеческого капитала. К 20 году совокупный человеческий капитал АСЭЭС России достигнет 39 млн. человек.
Качество человеческого капитала можно оценить уровнем его виртуальности :

Аналогичный подход можно реализовать и для удельного дифференциального уравнения, результаты будут определяться законом (функцией трансформации инвестиций на развитие человеческого капитала на душу населения в виртуальный прирост человеческого капитала на душу населения.

Список используемых источников

Варюхин А. М., Гришин П.Н. Элементы экономической трансформатики.
На пути к теории устойчивого развития агросистем: методологические осно-
вания и базовые модели.– Саратов : Изд-во Сарат. ун-та, 2012.
Варюхин А.М., Швейкин В.А. Аграрный ресурсно-производственный по-
тенциал как экономическая категория (сущность, содержание, диалектика
движения) // Материалы научных чтений, посвященных В.Б. Островскому).
"Островские чтения 2005" 23 ноября 2005 г. / РАН. Институт аграрных про-
блем. - Саратов, 2005.
Варюхин А.М., Кравченко В.В., Наташкин В.В. Системный анализ ресурс-
ного потенциала региональной агросистемы и методические подходы к его
комплексной оценке.- Саратов: Изд-во Сарат. гос. социально-эконом. уни-
верситета, 2000.
Варюхин А.М., Гришин П.Н. Использование эконометрических моделей
для оценки совокупного ресурсного потенциала сельскохозяйственного про-
изводства. Сб. научных работ специалистов и экономистов “Экономические
проблемы региона ’’ № 3-№4., Министерство экономики и инвестиционной
политики Саратовской области., 1997.
Данилов Н.Н. Курс математической экономики.- М.: Высш. шк., 2006.
6 .Клочков В. В. Человеческий капитал и его развитие. В книге: Экономиче-
ская теория. Трансформирующая экономика. / Под ред. Николаевой И. П. -
М.: Юнити, 2004
Колесов Ю.Б., Сениченков Ю.Б. Моделирование систем. Динамические и
гибридные системы. -Санкт Петербург: БХВ- Петербург 2006
Просолов А.В. Математические методы экономической динамики. – СПб.:
Издательство «Лань», 2008.
Урманцев Ю.А. Эволюционика или общая теория развития систем природы, общества и мышления. - М., 2009.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДИНАМИКИ ЧЕЛОВЕЧЕСКОГО КАПИТАЛА АГРОСИСТЕМЫ РОССИИ И ЕЕ РЕАЛИЗАЦИЯ СРЕДСТВАМИ ENGEE.

Тип

Краткое описание

Связанные материалы

Теги

Категории

Языки

Форматы

Уровень

Статус

Опубликовано

Обновлено

Источник