Многоаспектный анализ стратегий развития АПК России на больших временных горизонтах на основе использования моделей теории устойчивого развития агросистемы

Модели трансформации капитала агросистемы

Изложим подходы к построению динамических моделей, позволяющих включать в в анализ наиболее важные социально экономические и экологические параметры, детерминирующие процесс трансформации факторов развития агросистем. Рассмотрим основные соотношения и зависимости, лежащие в основе подобных моделей

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДИНАМИКИ ОСНОВНОГО КАПИТАЛА АГРОСИСТЕМЫ РОССИИ И ЕЕ РЕАЛИЗАЦИЯ СРЕДСТВАМИ ENGEE.

Все теоретические результаты, используемые в этом проекте, взяты из монографии автора [1,глава 4, параграф 4.1]

Материально-техническая база сельскохозяйственного производства является одной из важнейших составляющих капитала агросистемы. От уровня
ее развития, во многом, зависят её конечные результаты. В России до недавнего времени складывалась крайне неблагоприятная ситуация в сфере материально-технического обеспечения сельского хозяйства. Начиная, со второй половины 80-х годов постоянно снижался материально- технический потенциал аграрного производства. Наиболее интенсивно происходило сокращение активной части основных производственных фондов. Сокращалось применение минеральных и органических удобрений и средств химической защиты растений, снижалось потребление электроэнергии в производственных целях, электровооруженность труда и электрообеспеченность сельскохозяйственных угодий. Снижение объемных натурально-вещественных и стоимостных показателей основных производственных фондов сопровождалось ухудшением их структуры и качества (понизилась доля активной части, увеличился коэффициент износа). При этом ухудшалось соотношение между основными и оборотными фондами. Недостаточные инвестиции на расширенное воспроизводство основных фондов приводят к их физическому и моральному старению.
В структуре материальных затрат происходит перераспределение затрат с обеспечения биологических условий сельскохозяйственного производства
на обеспечение функционирования механических средств труда. Отмеченные отрицательные тенденции в развитии основного капитала
агросистемы России наиболее рельефно проявлялись в 90-е годы, но сейчас многие из этих негативных явлений устраняются,что начинает определять позитивный тренд его динамики. Учитывая основные тенденции развития основного капитала агросистемы России, и формулируя определенные гипотезы относительно его долговременной динамики, попытаемся построить соответствующую динамическую математическую

Движение основного капитала в дискретном времени может быть представлено уравнением:

где
- коэффициент выбытия фондов;
- прирост фондов за счет инвестиций;
- катастрофические потери фондов.

Тогда коэффициент трансформации (индекс развития основного капитала) может быть представлен следующим образом:

где
; - \text{инвестиции} \text{в} \text{основной} \text{капитал}; -
инвестиции в основной капитал за счет собственной прибыли; -- инвестиции в основной капитал за счет дополнительных источников (заем-ные средства);
, коэффициент катастрофических потерь фондов.
Или имеем:

где - коэффициент (индекс), характеризующий остаточный уровень развития фондов; коэффициент трансформации инвестиций в основной капитал. Здесь -коэффициент, характеризующий качество и структуру остаточных фондов. Если этот коэффициент меньше единицы, то фонды не соответствуют на данный момент времени общественно необходимому уровню по качеству и структуре (средний уровень по группе экономически развитых стран). При значении этого коэффициента больше единицы они превосходят по структу-ре и качеству общественно необходимый уровень развития фондов.
Коэффициент характеризует уровень инновационности использования инвестиций для формирования основного капитала. При инвестиции используются ниже общественно необходимого уровня (средний уровень по группе экономически развитых стран), а при выше. Данный коэффициент в концентрированном виде выражает качество развития основного капитала агросистемы.
Типы развития основного капитала можно проиллюстрировать следу-ющим образом (рис. 1):

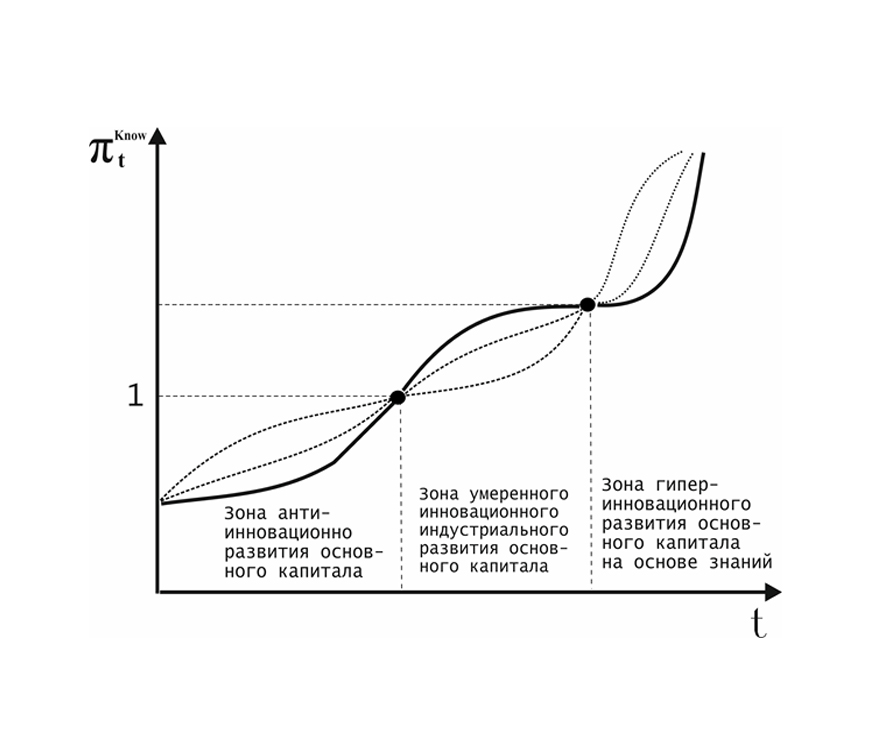
Таким образом, возможность развития основного капитала (производственных фондов) агросистемы определяется рядом факторов: возрастом и изношенностью фондов (коэффициент ),качеством и структурой ( коэффициент ),общей массой фондов (),объёмом инвестиций в основной капитал () и уровнем инновационности использования инвестиций ( коэффициент ) и возникновением катастрофических событий ().Основное дискретное динамическое соотношение:

Перейдем от дискретного к не прерывному времени. Вычитая из обеих частей уравнения (4) получим следующее уравнение:

Переходя к бесконечно малым приращениям, получаем следующее дифференциальное уравнение:

Если в уравнении (4) обе части разделить на и учитывая, что , где - естественный прирост населения, то получим удельное уравнение на душу населения:

где и основной капитал на душу населения соответственно в t+1 и t периоды времени. Тогда и переходя к малым приращениям, получаем удельное дифференциальное уравнение:

Где -инвестиции в основной капитал на душу населения в период t.
Найдем экономически целесообразные временные законы изменения па-раметров, входящих в правую часть дифференциального уравнения (7) при которых решение этого уравнения представляет положительную возрастающую функцию времени. Предположим, что изменение основных параметров в правой части описывается S-образными функциями времени на интервале [0,20], а . Пусть имеем:

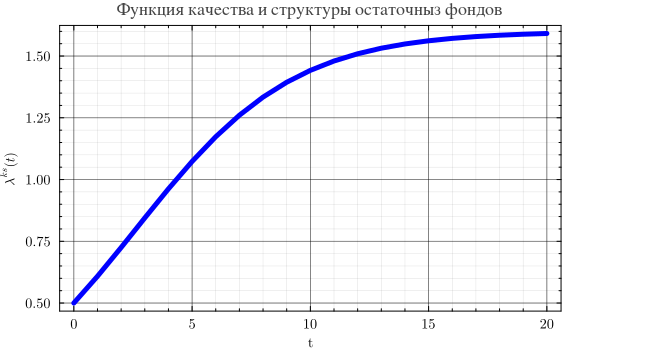
Изменение качества и структуры остаточных фондов аграрного производства описывается логистической функцией (см. ниже). В момент времени t=0 . то есть их уровень составляет 50 процентов от общественно необходимого уровня. При , то есть на 60 процентов выше общественно необходимого уровня.

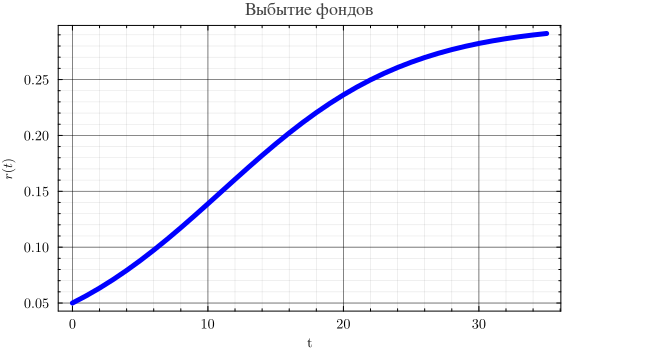
Выбытие фондов описывается логистической функцией:

В момент времени изношены и их выводится из оборота 5 процентов в год (цикл обновления 20 лет), они заменяются морально устаревшими фондами. При в приделе предполагается ежегодная замена 30 процентов фондов (цикл обновления 3-4 года) современным оборудованием.

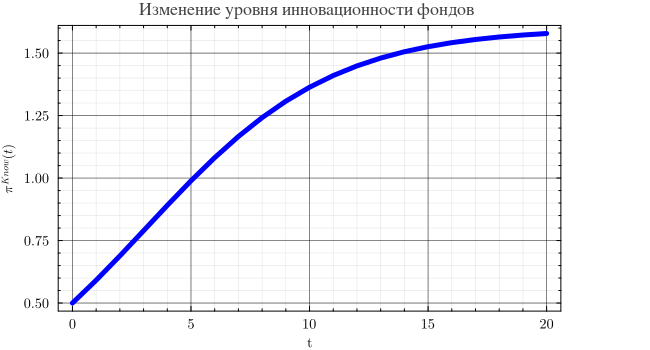
Изменение уровня инновационности фондов в аграрной сфере опишем следующей логистической функцией:

В момент времени в начальный момент имеем 50 процентный от общественно необходимого уровня инновационности развития фондов аграрного производства. При в приделе предполагается достигнуть 60 процентного превышения общественного необходимого уровня инновационности в развитии фондов.

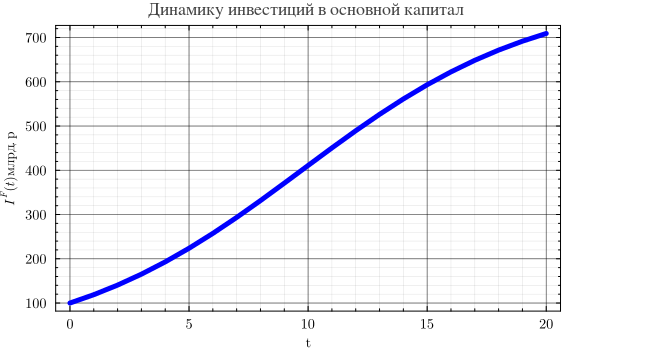
Динамику инвестиций в основной капитал аграрного производства опишем следующей функцией:

В момент времени годовые инвестиции в основной капитал аграрной сферы принимаем
млрд. рублей. При млрд.рублей.

Тогда имеем следующее дифференциальное уравнение:

Где

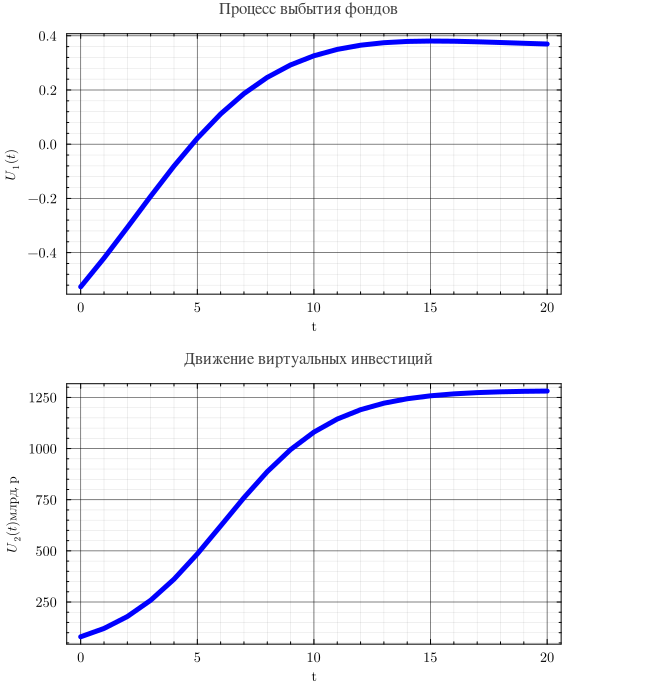
Функция описывает процесс выбытия фондов с учетом качества и структуры остающихся фондов, а функция наращивания и обновления фондов за счет инвестиций с учетом инновационности вложений в основной капитал аграрного производства.
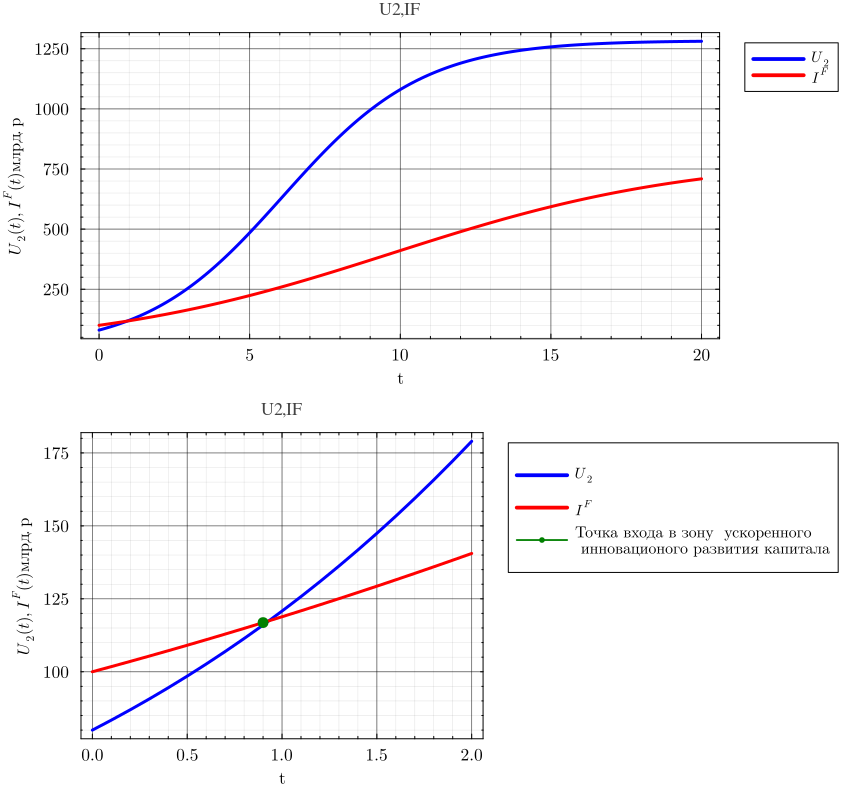
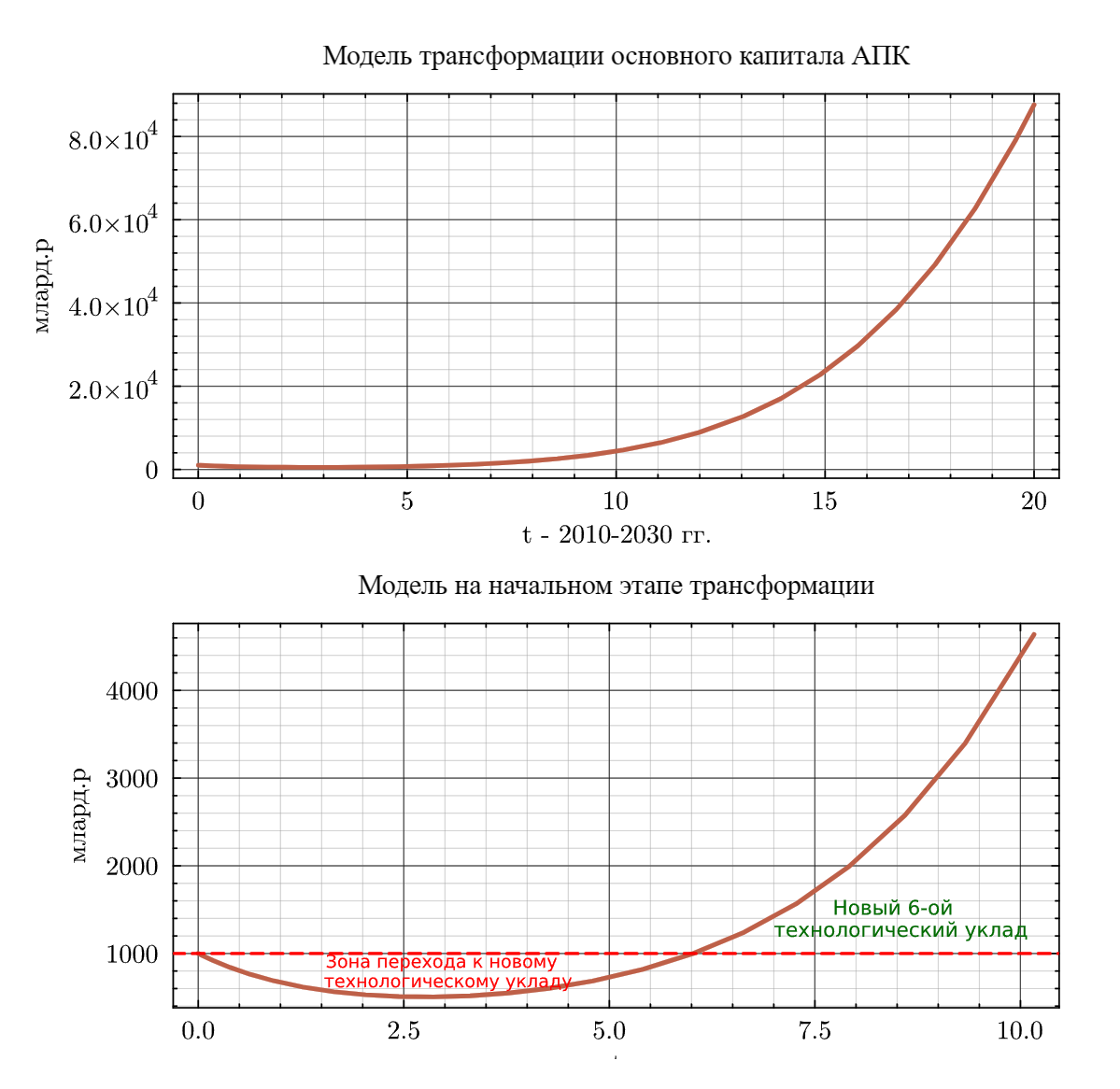
При этом функция описывает движение «виртуальных» инвестиций, которых меньше чем реальных, если уровень инновационности их использования, ниже среднего по развитым странам и больше реальных, если уровень инновационности их использования выше среднего по развитым странам.Сравнение движения реальных и «виртуальных» инвестиций представлено на графике (см. ниже). Численное решение дифференциального уравнения (14) при млрд.рублей представлено на графике (см. ниже)
Как видно из графика первые 3 года основной капитал падает вдвое, так как предельно устаревшие фонды не успевают заменятся новыми,а затем за счет роста инновационных инвестиций начинается накопление современного основного капитала и к 6 году достигается его начальный уровень, а затем начинается его быстрое инновационное лавинное нарастание,характеризующее переход АПК России к новому 6-му технологическому укладу

Рассмотрим уравнение (9) в условиях России можно считать, что и тогда:

Или ГДЕ численность населения
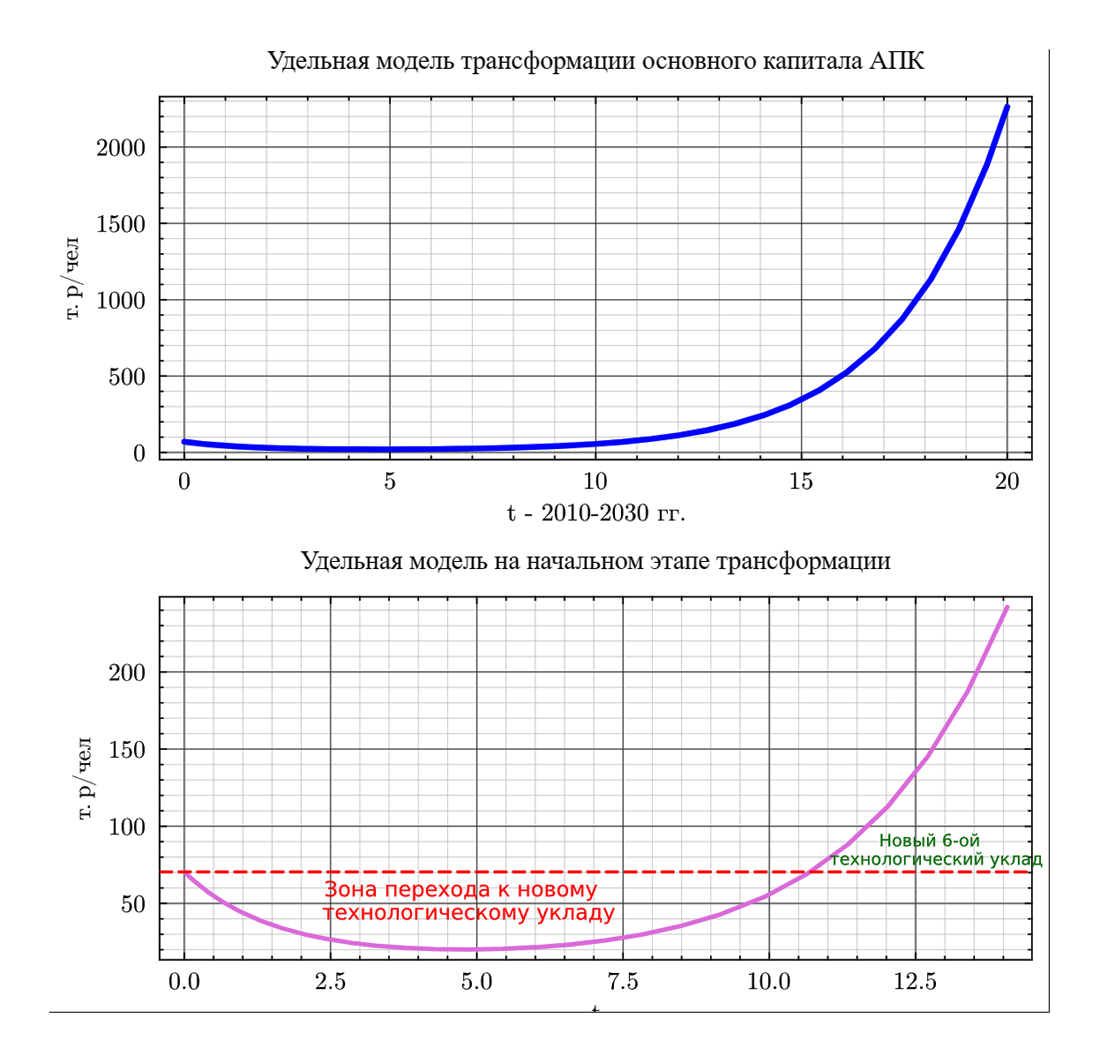
(млн. чел.) Численно решая это уравнение, при (руб.чел) получаем следующее решение для основного капитала на душу населения (см ниже). Естественно, что при неизменном населении (а для России это достаточно реальный вариант демографического развития) основной капитал на душу населения имеет тот же закон, что и .

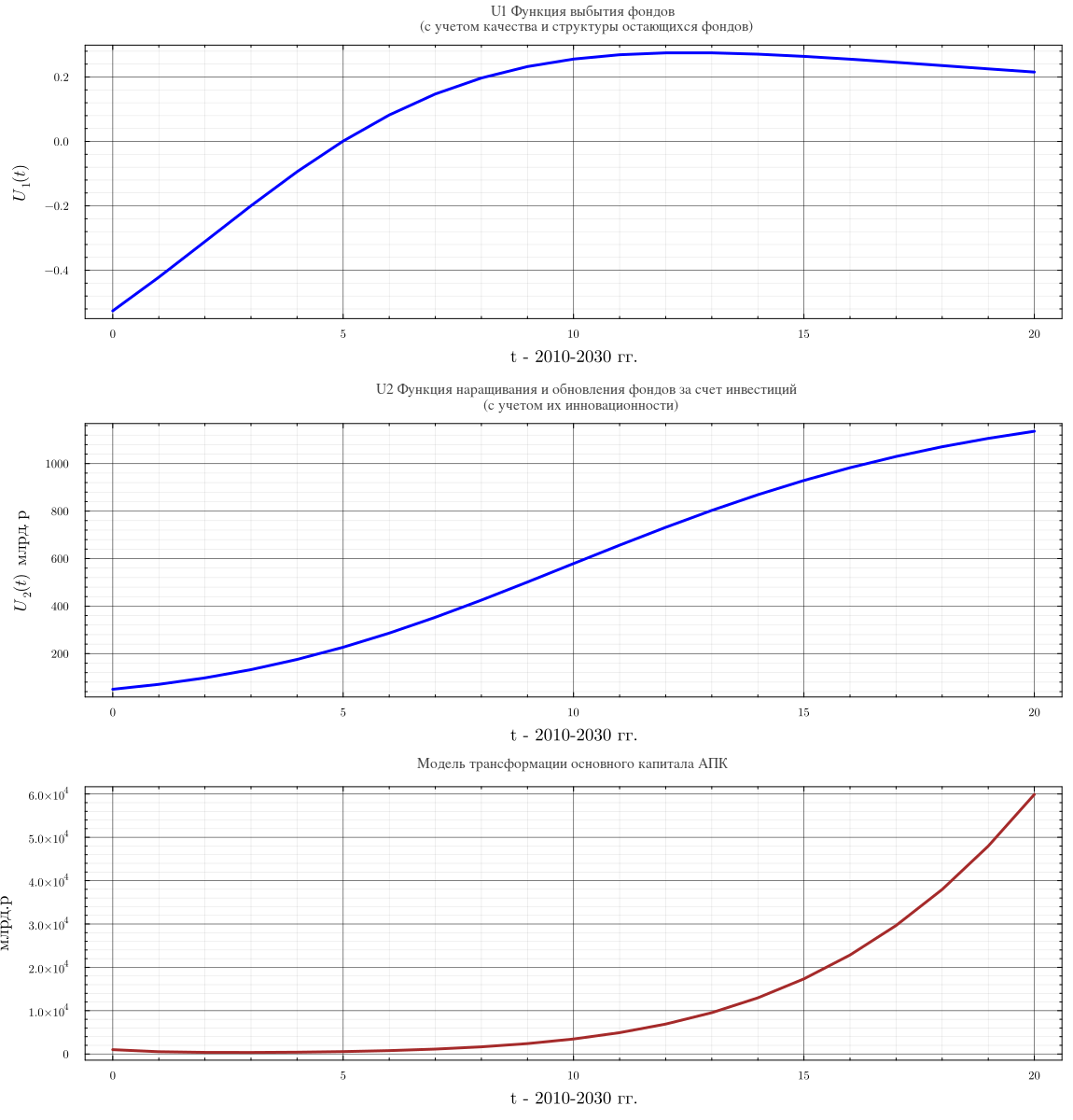
Реализующая решение уравнения (14) при начальных условиях F(0) = 1000 млрд.рублей на интервале t=[0.0,20.0] Engee-модель «F0.mdl» имеет
следующий вид :

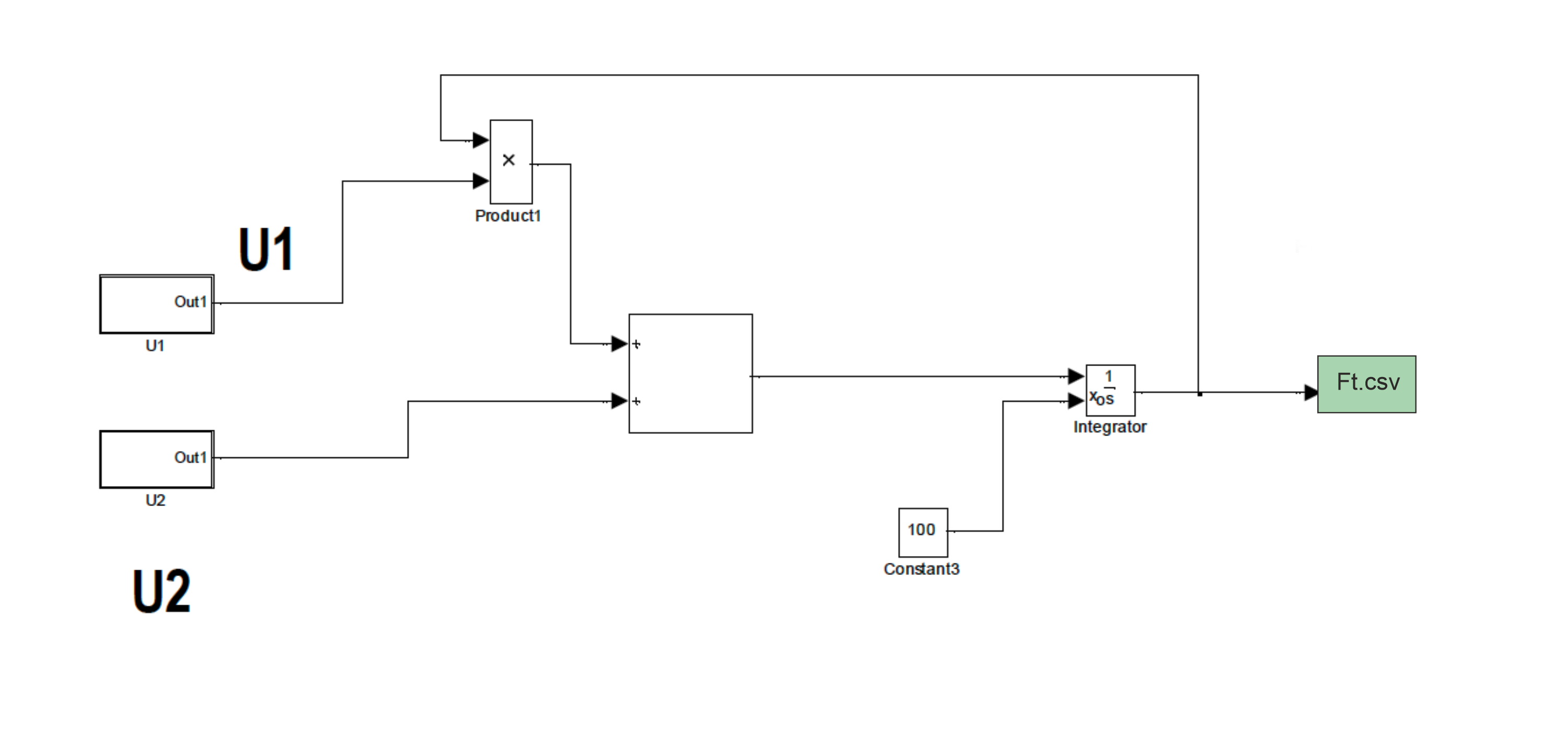
В этой Engee-модели используются две подмодели «U1», «U2». Подмодели реализуют функции U1(t) и U2(t) соответственно и имеют следующий вид ( c =0.015496):

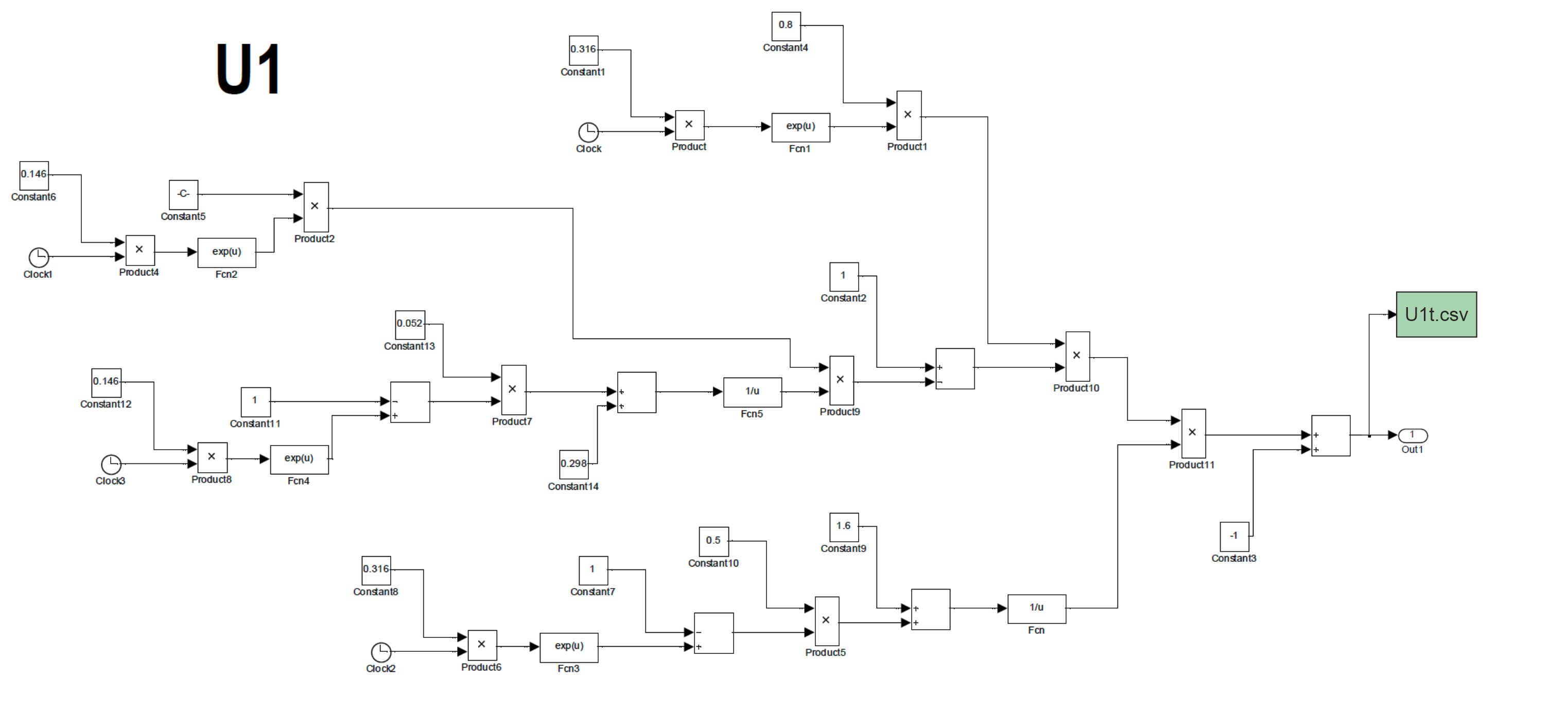
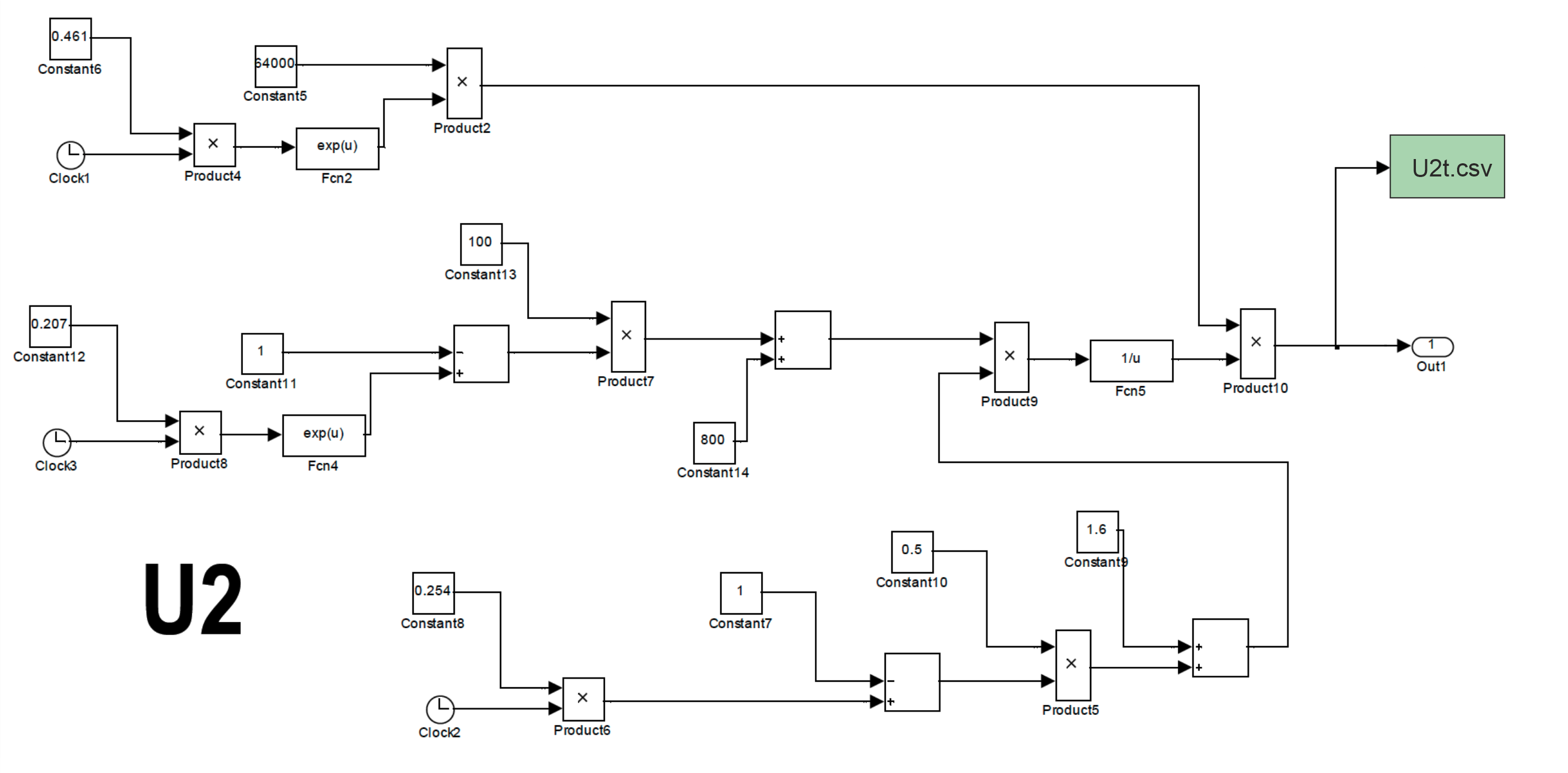
Для исследования с помощью этой модели динамики основного капитала агросистемы России был разработан соответствующий скрипт julia. Ре-
зультаты решения представлены ниже.

Как видно из графика динамики (рис 9) при предложенной иновационно-инвестиционной стратегии первые 5 лет основной капитал не растет, идет замена предельно устаревших фондов, затем следующие пять лет идет постепенное накопление современного основного капитала, а затем его быстрое инновационное нарастание. Разработанные математическая модель и программный инструментарий позволяют исследовать динамику основного капитала агросистемы России при самых различных инновационных и инвестиционных стратегиях.

Список используемых источников

1. Варюхин А. М., Гришин П.Н. Элементы экономической трансформатики.
   На пути к теории устойчивого развития агросистем: методологические осно-
   вания и базовые модели.– Саратов : Изд-во Сарат. ун-та, 2012.

2. Варюхин А.М., Швейкин В.А. Аграрный ресурсно-производственный по-
   тенциал как экономическая категория (сущность, содержание, диалектика
   движения) // Материалы научных чтений, посвященных В.Б. Островскому).
   "Островские чтения 2005" 23 ноября 2005 г. / РАН. Институт аграрных про-
   блем. - Саратов, 2005.

3. Варюхин А.М., Кравченко В.В., Наташкин В.В. Системный анализ ресурс-
   ного потенциала региональной агросистемы и методические подходы к его
   комплексной оценке.- Саратов: Изд-во Сарат. гос. социально-эконом. уни-
   верситета, 2000.

4. Гилфасон Т. Ресурсы, сельское хозяйство и экономический рост в странах
   с переходной экономикой. // ЭКОВЕСТ (2002)

5. Варюхин А.М., Гришин П.Н. Использование эконометрических моделей
   для оценки совокупного ресурсного потенциала сельскохозяйственного про-
   изводства. Сб. научных работ специалистов и экономистов “Экономические
   проблемы региона ’’ № 3-№4., Министерство экономики и инвестиционной
   политики Саратовской области., 1997.

6. Урманцев Ю.А. Эволюционика или общая теория развития систем приро-
   ды, общества и мышления. - М., 2009.

7. Данилов Н.Н. Курс математической экономики.- М.: Высш. шк., 2006.

8. Просолов А.В. Математические методы экономической динамики. – СПб.:
   Издательство «Лань», 2008.

9. Колесов Ю.Б., Сениченков Ю.Б. Моделирование систем. Динамические и
   гибридные системы. -Санкт Петербург: БХВ- Петербург 2006.

10. Абакумов Р.Г. Управление воспроизводством основного капитала как ус-
    ловие инновационного пути развития экономики // Креативная экономика.- 2009.

11. Козельский А. В. Развитие основного капитала как фактора формирова-
    ния нового качества экономического роста : дис. ... канд. экон. наук : 08.00.01
    Саратов, 2006