Моделирование динамики природного капитала АПК России
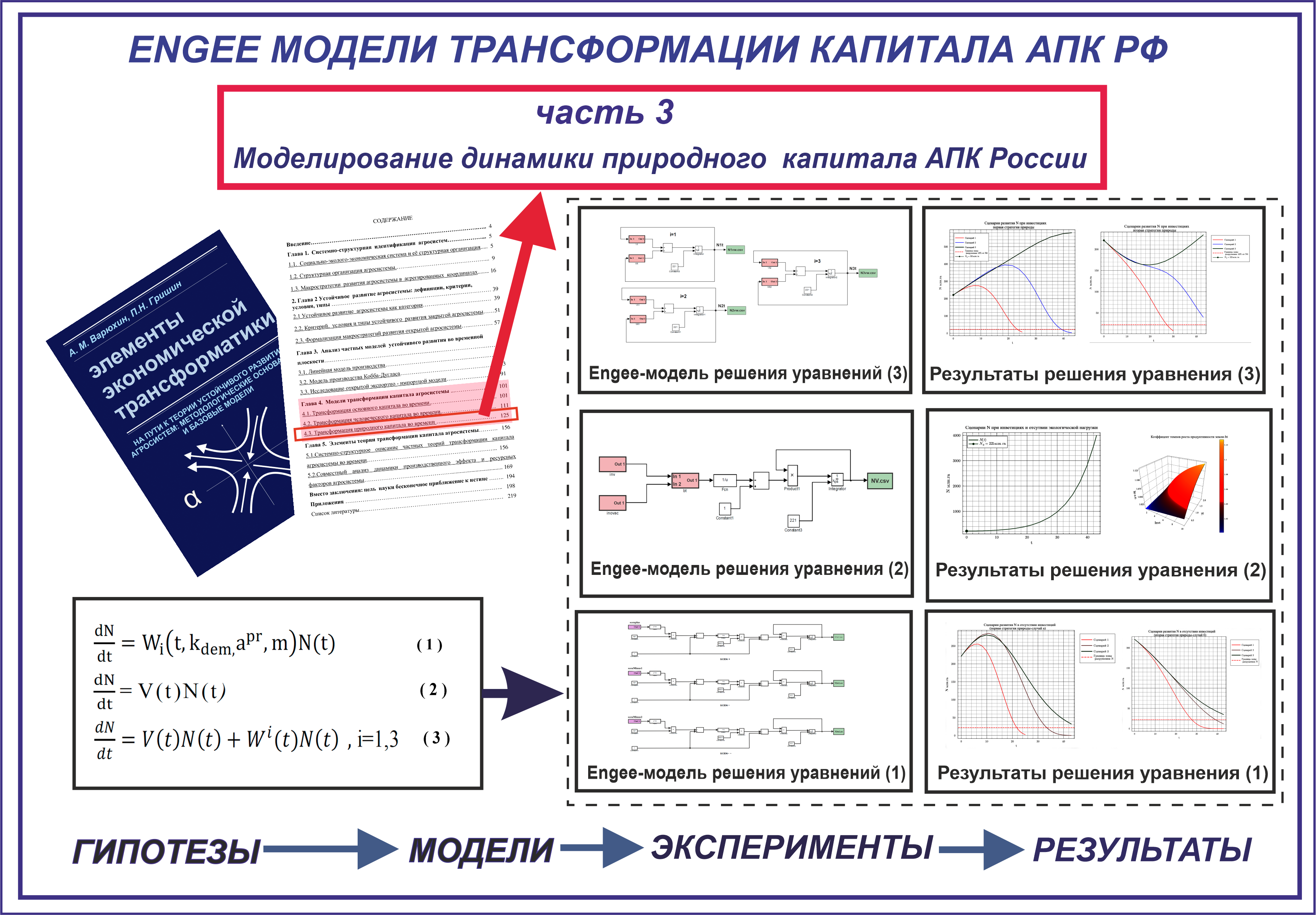
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДИНАМИКИ ПРИРОДНОГО КАПИТАЛА АГРОСИСТЕМЫ РОССИИ И ЕЕ РЕАЛИЗАЦИЯ СРЕДСТВАМИ ENGEE.
Все теоретические результаты, используемые в этом проекте, взяты из монографии автора [1,глава 4, параграф 4.3]
Представим процесс движения природно-экологического (естественного) капитала в дискретном времени следующим уравнением:
Где
- природно-экологический потенциал соответственно в момент времени ;
- уменьшение природного потенциала за счет негативной (природа разрушительной) деятельности человека (общества);
-увеличение природного потенциала за счет позитивной (природа восстановительной) деятельности человека (общества);
- увеличение природного потенциала за счет естественных механизмов воспроизводства природного капитала;
- уменьшение природного потенциала за счет естественных причин (глобальное изменение климата, почвы и.т. д.).
Здесь
и - функция трансформации инвестиций в прирост природного капитала, - характеризует уровень инновационности использования инвестиций для формирования природного капитала. При инвестиции используются ниже общественно необходимого уровня, а при выше. Данный коэффициент в концентрированном виде выражает качество искусственного развития природного капитала агросистемы.
Для природного капитала очень важны естественные процессы роста (самовосстановления) и деградации. То есть, имеем, , где .. Здесь коэффициент, характеризующий естественное самовозрастание природного капитала, , регулярная и стохастическая составляющие данного коэффициента,
- предельное верхнее значение коэффициента
Для , где . Здесь коэффициент, характеризующий естественное убывание природного капитала, регулярная и стохастическая составляющие данного коэффициента. В пределе считаем, что природный капитал может быть уничтожен за счет естественных причин, например природных катаклизмов.
Следовательно, имеем:
Из выражения (2) видно, что развитие природно-экологического капитала определяется естественными природными процессами, формирующими естественный прирост и убыль природного капитала , социально политическими и экономическими процессами, детерминирующими негативное антропогенное воздействие на природный капитал , уровнем инвестиций в природоохранную деятельность и уровнем инновационности использования инвестиций в развитие природного капитала . Основное дискретное динамическое соотношение:
Перейдем от дискретного к не прерывному времени. Вычитая из обеих частей уравнения (3) получим следующее уравнение:
Переходя к бесконечно малым приращениям, получаем следующее дифференциальное уравнение:
Получим удельное динамическое уравнение для человеческого капита-ла в дискретном времени:
, где и природный капитал на душу населения соответственно в и периоды времени.
и переходя к малым приращениям, получаем удельное дифференциальное уравнение:
Рассмотрим соотношение (5), сформулировав некоторые экономически и экологически правдоподобные гипотезы, задающие соответствующие тренды членов правой части данного дифференциального уравнения.
Обратимся сначала к функции, являющейся переменным коэффициентом при уровне природного капитала АСЭЭС в момент :
Здесь представлены три составляющих и характеризуют естественные процессы повышения (снижения) размера и качества природного капитала АСЭЭС, а описывает его разрушение в результате человеческой деятельности.
Прежде всего, необходимо определить само понятие «природный капитал аграрного производства». Приведем здесь только предварительные соображения по данному вопросу, которые достаточны для демонстрации возможностей сформулированных выше моделей динамики природного капитала агросферы.
И так, в качестве природного капитала нами рассматривается подсистема природной системы, которая включается в процесс аграрного производства в качестве предмета или орудия труда, то есть это те природные объекты и силы, без которых невозможно в современных социально-экономических условиях производство сельскохозяйственной продукции.
Естественной основой аграрного производства является территория, обладающая определенными топологическими и климатическими свойства (форма, рельеф, площадь, типы почв, наличие водоемов, годовое количество солнечной энергии, температурный режим, уровень влажности и т.п). Неравномерность распределения этих свойств по территории приводит к формированию ареалов, где имеется такой набор этих свойств, что естественные природные силы возможно и целесообразно использовать в данных кокретно-исторических условиях для сельскохозяйственного производства. Именно эти ареалы территории - есть естественная основа природного капитала АСЭЭС, в качестве которого выступает, прежде всего, земля сельскохозяйственного назначения.
Основными характеристиками, отражающими производительные возможности природного капитала АСЭЭС, являются размер земельных угодий (площадь), плодородие земли, биоклиматический потенциал (БКП), уровень аграрной освоенности территории (отношение площади земель аграрного назначения к площади территории), пространственно-топологические характеристики (форма, расположение относительно центров социальной и экономической активности) и инфраструктурная обеспеченность.
Поэтому при оценке возможных трендов и на ближайшие 20-40 для АСЭЭС России мы будем анализировать возможную динамику именно этих составляющих природного капитала.
Выше мы ввели соотношение , если рассматривать регулярную составляющую, то за сценарный период (20-40 лет) трудно предполагать наличие отрицательной естественной динамики. Сокращение площади сельскохозяйственных угодий России за счет естественных причин (поднятие уровня мирового океана, опустынивание и.т. д.), маловероятно, по крайней мере, общепризнанных прогнозов такого плана нет.
БКП также не имеет явных тенденций к изменению (глобальное изменение климата если даже и происходит, то в рассматриваемом временном масштабе оно, по нашему мнению, ничтожно мало), не предвидится естественное отрицательное изменение уровня естественного плодородия почв и соответствующих пространственно-топологических характеристик [130,131].
Следовательно, можно принять , случайная составляющая связана в основном с климатическими факторами, а они, как показывают многолетние наблюдения, являются нормально распределенными случайными величинами с нулевым математическим ожиданием и не очень большой на периоде 20-40 лет дисперсией, поэтому полагаем
Что касается процессов естественного роста природного капитала , то проблема здесь достаточно сложна и общепризнанных подходов системного интегрального характера, по нашему мнению нет, мы все же постараемся их учесть в рамках предлагаемых моделей.
Но вполне очевидно, что в модель можно включать, если это необходимо, эффекты и как в дискретном, так и непрерывном вариантах.
Рассмотрим, как формируется отрицательный виртуальный прирост природного капитала АСЭЭС за счет уменьшения продуктивности земли. Пусть в момент – продуктивность единицы площади земли и площадь сельскохозяйственных угодий (полагаем , тогда , где объем сельскохозяйственной продукции, аналогично имеем При этом имеет место следующее соотношение –коэффициент характеризующий темп падения продуктивности земли момент времени , тогда отсюда:
,следовательно, имеем отсюда , где где виртуальная площадь сельхозугодий, которую нужно было бы иметь, чтобы получить объем сельхозпродукции равный .Тогда виртуальный прирост природного капитала:
Величина , определяющая продуктивность земли в любой момент времени, зависит от экологической нагрузки, которая оказывает экономика на природный капитал АСЭЭС. В качестве измерителя нагрузки возьмем относительную экологическую нагрузку как отношение текущей нагрузки на максимально допустимую, то есть такую нагрузку, при которой уровень продуктивности земли таков, что начинается резкое снижение качества жизни в связи с невозможностью обеспечить население продуктами питания в необходимом количестве и качестве.
Определение придельной экологической нагрузки рассмотрим ниже. Ясно, что относительная экологическая нагрузка должна представлять собой монотонно возрастающую функции времени с интервалом значений то есть, имеем: .
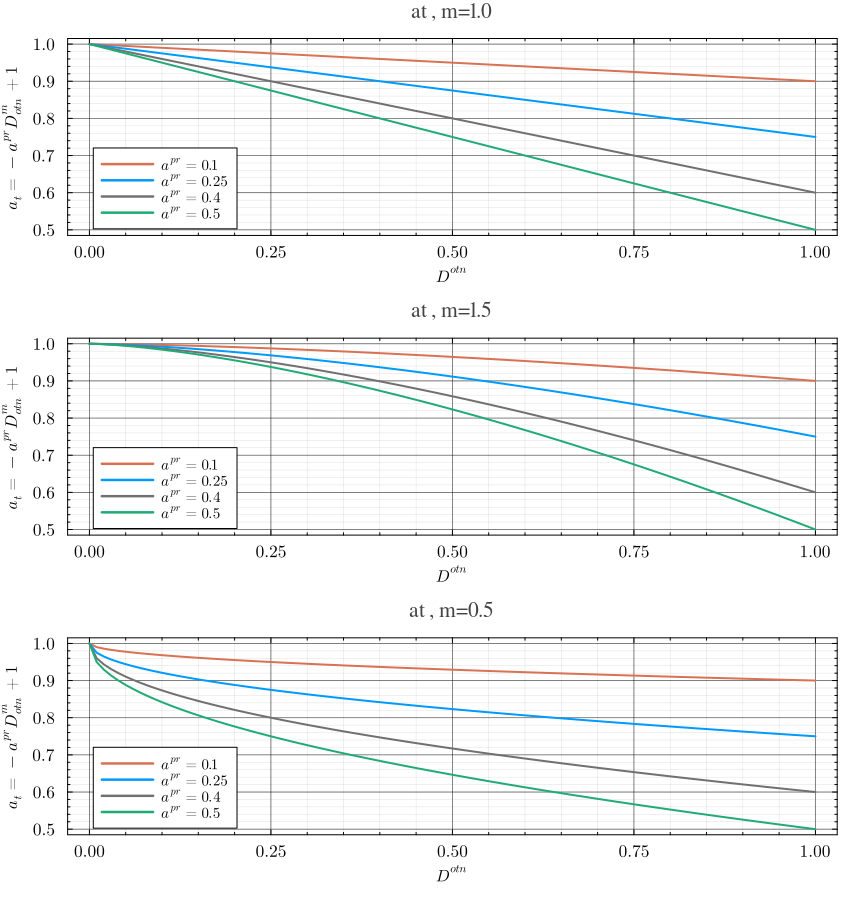
Коэффициент темпа падения продуктивности земли из естественных соображений представляет собой монотонно убывающую функцию на интервале . При этом в отсутствии нагрузки он должен принимать значение равное 1 , при придельной нагрузке значение , определяющее максимальный темп падения продуктивности земли, при котором фактически начинается структурно-функциональное разрушение национальной АСЭЭС. Предельное значение (отрицательный прирост природного капитала при этом равен его первоначальному значению). Можно предложить следующие классы моделей падения продуктивности земли от уровня относительной экологической загрузки:
где параметр задает скорость и характер падения . При имеем линейное падение с постоянной скоростью (а), при нелинейное падение с увеличивающейся скоростью (б) и при нелинейное падение с уменьшающейся скоростью (в).
using RDatasets, Plots, PlotThemes
using DataFrames
using LaTeXStrings
apr=[0.1,0.25,0.4,0.5]
Dotn = (0.0:0.01:1.0)
Met = [L"a^{pr}=0.1", L"a^{pr}=0.25", L"a^{pr}=0.4", L"a^{pr}=0.5"]
#Colat=["green","red","blue","yellow4"]
gr()
#plotly()
#theme(:ggplot2)
theme(:dao)
default(titlefont=(14, "times"), legendfontsize=10, guidefont=(11, :black), tickfont=(11, :black) )
p1=plot(wsize=(650, 450))
m = 1.0
for i in 1:4
at=@.(-(apr[i]*Dotn^m)+1)
p1=plot!(Dotn,at,label=Met[i], lw=2)
end
p1=plot!(title="at , m=$m")
p2 = plot(wsize=(650, 450))
m = 1.5
for i in 1:4
at = @.(-(apr[i] * Dotn^m) + 1)
p2=plot!(Dotn, at, label=Met[i], lw=2)
end
p2 = plot!(title="at , m=$m")
p3 = plot(wsize=(650, 450))
m = 0.5
for i in 1:4
at = @.(-(apr[i] * Dotn^m) + 1)
p3 = plot!(Dotn, at, label=Met[i], lw=2)
end
p3 = plot!(title="at , m=$m")
plot(p1, p2, p3, layout=(3, 1), wsize=(850, 900), xlabel=L"D^{otn}", ylabel=L"a_t=-a^{pr}D_{otn}^{m}+1",legend = true)
Перейдем к оценке относительной экологической нагрузки. В качестве измерителя предлагаем использовать следующее выражение: , где P(t) - функции описывающая динамику ВВП ; – антропогенная нагрузка, разрушающая природный потенциал, как функция ВВП; – предельно допустимая нагрузка, при которой природный потенциал АСЭЭС разрушается полностью.
Для оценки этой функции для России на период до 50 лет воспользуемся результатами глобального моделирования мирового развития [Римский клуб]. Для иллюстрации предлагаемых подходов выбираем два сценария пессимистический (сценарий 7) (рис.) и оптимистический (сценарий 9) (рис. ):
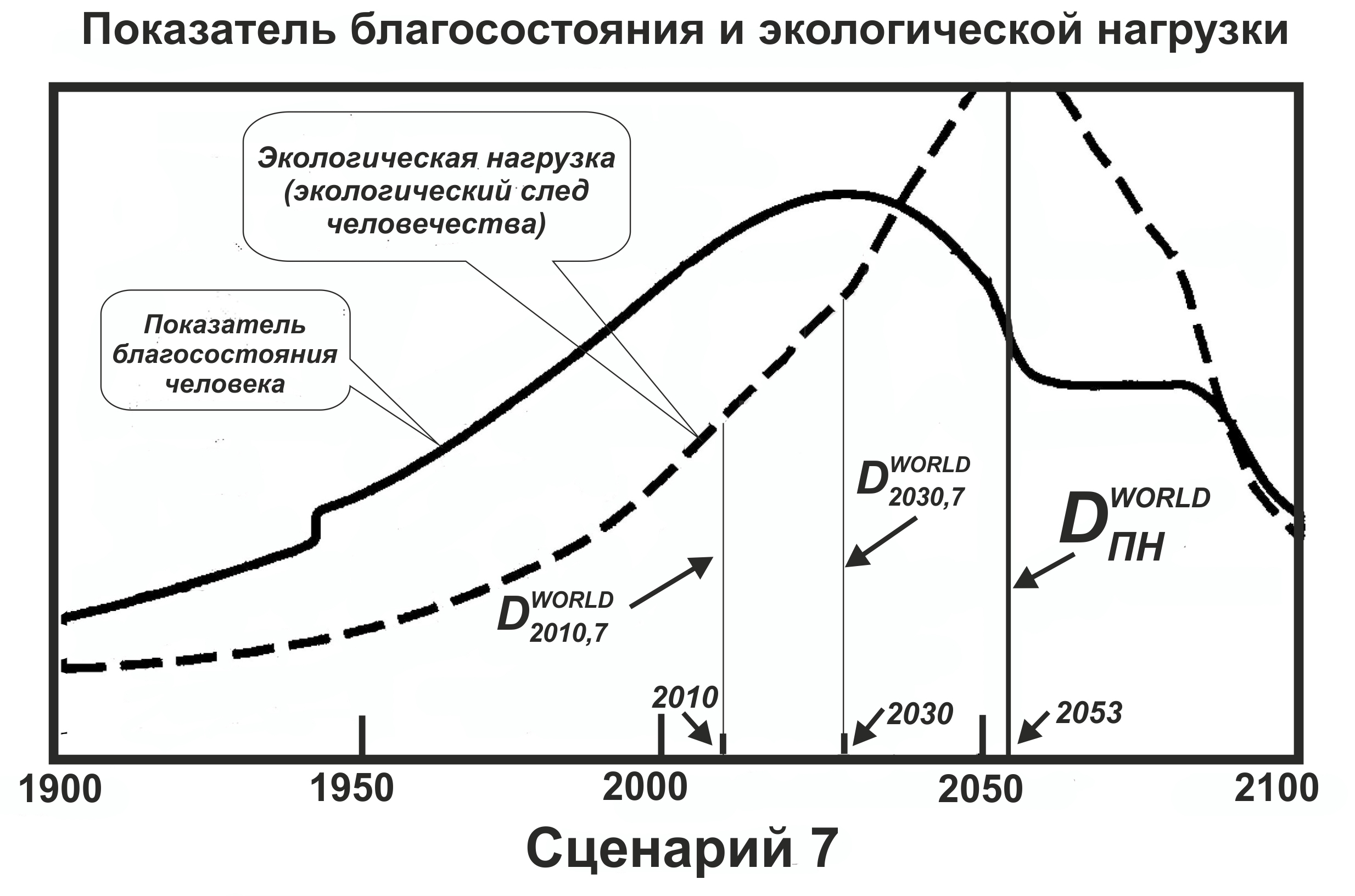
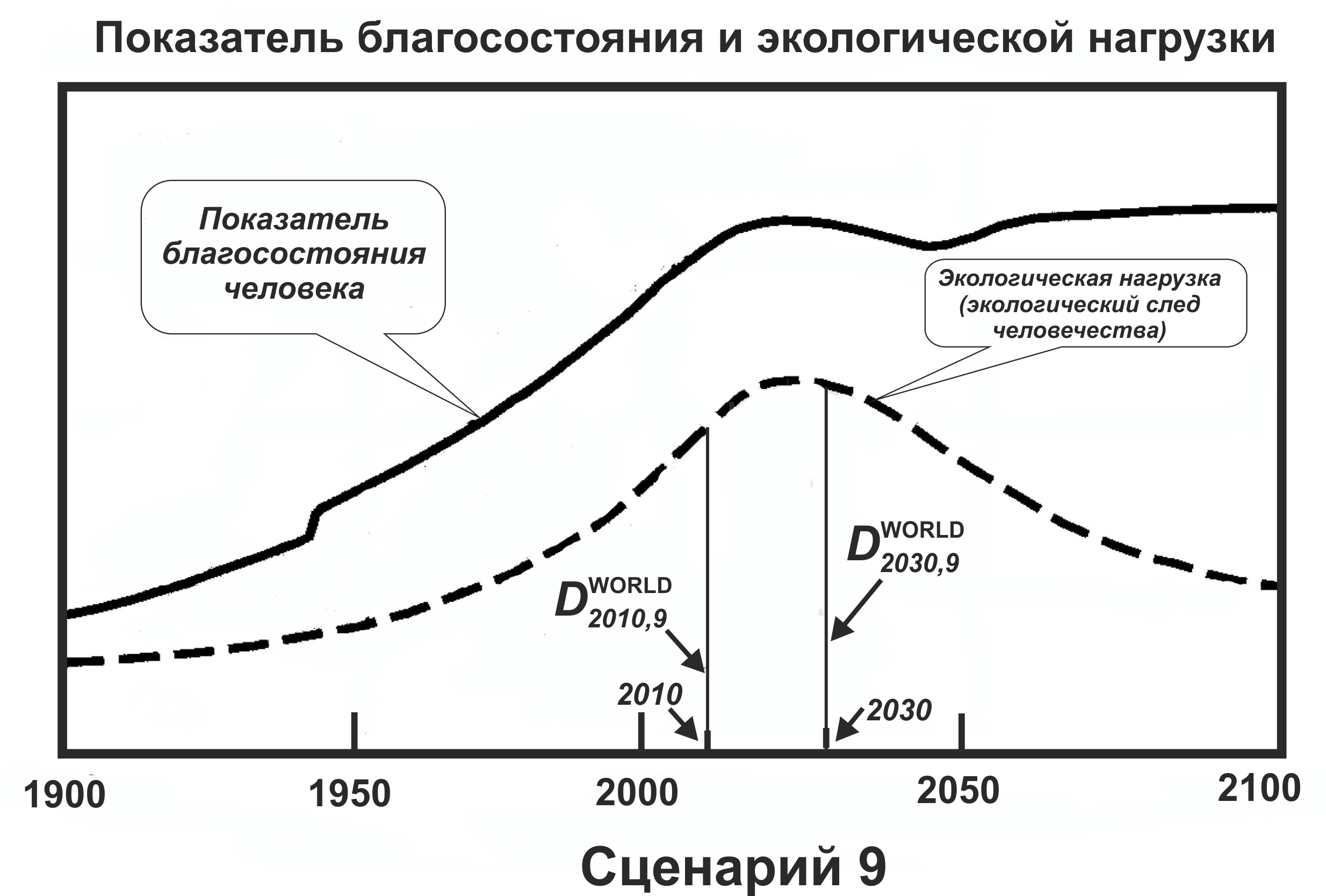
Сценарий 9 предполагает в перспективе постепенную стабилизацию населения, снижение темпов роста экономики, повышение ее инновационности и экологичности. В сценарии 7 предполагается сохранение, и даже усиление существующих негативных тенденций развития.
На графике сценария 7 приблизительно на 2053 год приходится максимум экологической нагрузки, которая равна 106 относительных единиц. Будем считать, что это предельная экологическая нагрузка человечества:
Для определения значения предельной экологической нагрузки для России определим прогноз доли ВВП России в мировом ВВП на 2053 год. По данным ЦРУ США ВВП России по паритету покупательной способности в 2010 году составил 2.99 процента от мирового. Если считать, что мировой ВВП будет расти в среднем 2 процента в год, а ВВП России в среднем 4 процента в год, то доля России в мировом ВВП к 2053 году может составить порядка 6.9 процента. Следовательно, можно принять
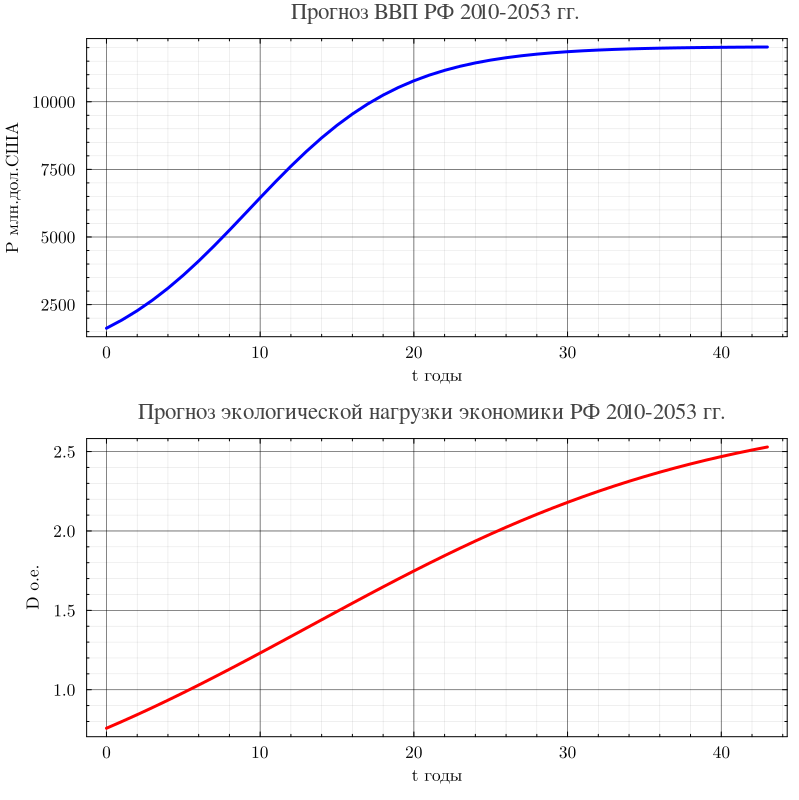
Для построения функции сначала сконструируем функцию прогноз изменения ВВП России на период 2010-2053 гг. Будем исходить из оптимистического предположения, что среднегодовой темп роста составит 4 процента, тогда млн. долларов США (фактически 2010 г.), а в конце сценарного срока 2053 год млн. долларов США.
Наиболее вероятной динамической моделью ВВП России на данный период лет мы считаем логистическую функцию, хорошо описывающую быстро растущие экономики в период перехода мировой экономике к повышательной фазе длинноволнового К-цикла (переход к 6 технологическому укладу). Следовательно:
Что касается экологической нагрузки, то, при принятом выше, сценарии динамики ВВП России целесообразно использовать откорректированный по ВВП сценарий 7 глобального развития, где начальное и конечное значения равны о.е. ,а о.е. :
using Plots, PlotThemes
using LaTeXStrings
t =(0.0:1.0:43.0)
Pt = @.((12038 * 2229 * exp(0.2 * t)) / (12038 + 2229 * (exp(0.2 * t) + 1)))
Dt = @.((2.8 * 1.65 *exp(0.075 * t)) / (2.8 + 1.65 * (exp(0.075 * t) + 1)))
gr()
#plotly()
theme(:dao)
default(titlefont=(14, "times"), legendfontsize=10, guidefont=(11, :black), tickfont=(11, :black))
p1 = plot(t, Pt, lw=3, title="Прогноз ВВП РФ 2010-2053 гг.", xlabel="t годы", ylabel="P млн.дол.США", lc=:blue)
p2 = plot(t, Dt, lw=3, title="Прогноз экологической нагрузки экономики РФ 2010-2053 гг. ", xlabel="t годы", ylabel="D o.e.", lc=:red)
plot(p1, p2, layout=(2, 1), wsize=(800,800), legend=false)
Экономический смысл заключается в следующем, первые 30 лет используются относительно экологоемкие факторы роста, быстро увеличивающие экологическую нагрузку, а затем более инновационные и экологически чистые способы повышения ВВП.
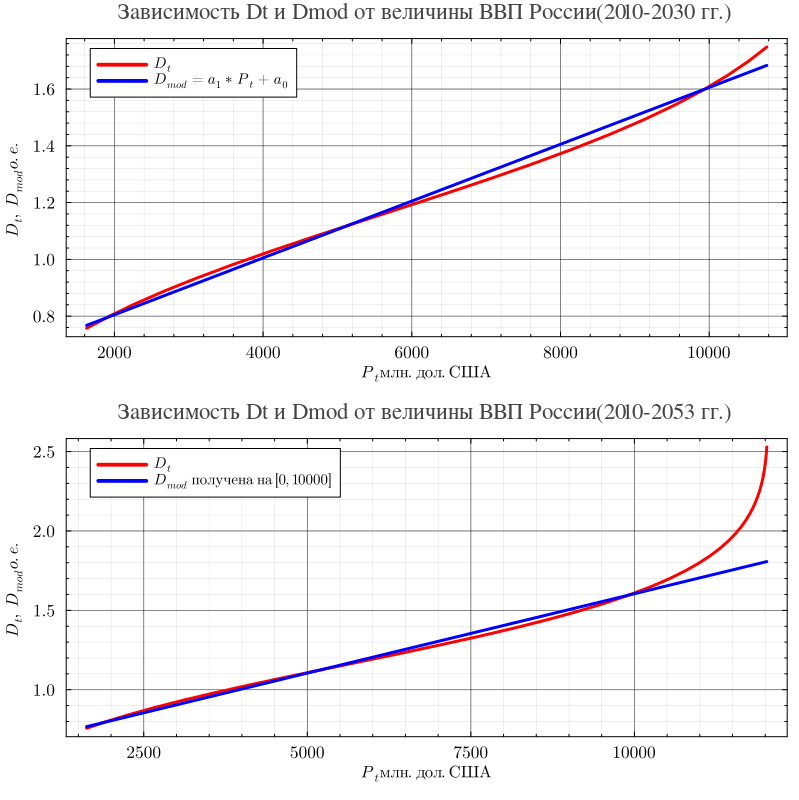
Зависимость , построенная на основе выше вышеприведенных соотношений имеет вид:
using Plots, PlotThemes
using LaTeXStrings
using DataFrames, GLM, StatsBase
t = (0.0:1.0:20.0)
Pt = @.((12038 * 2229 * exp(0.2 * t)) / (12038 + 2229 * (exp(0.2 * t) + 1)))
Dt = @.((2.8 * 1.65 * exp(0.075 * t)) / (2.8 + 1.65 * (exp(0.075 * t) + 1)))
data = DataFrame(X=Pt, Y=Dt);
mod = lm(@formula(Y ~ X), data)
Dmod = round.(predict(mod), digits=5)
Koif = round.(coef(mod), digits=5)
gr()
#plotly()
theme(:dao)
default(titlefont=(14, "times"), legendfontsize=10, guidefont=(11, :black), tickfont=(11, :black))
p1=plot(Pt, Dt, lw=3, title="Зависимость Dt и Dmod от величины ВВП России(2010-2030 гг.)", xlabel=L"P_t млн.дол.США",
ylabel=L"D_t ,\;D_{mod} o.e.", lc=:red,label=L"D_t")
plot!(Pt, Dmod, lw=3, lc=:blue, label=L"D_{mod}=a_1*P_t +a_0")
t = (0.0:1.0:43.0)
Pt = @.((12038 * 2229 * exp(0.2 * t)) / (12038 + 2229 * (exp(0.2 * t) + 1)))
Dt = @.((2.8 * 1.65 * exp(0.075 * t)) / (2.8 + 1.65 * (exp(0.075 * t) + 1)))
Dmod = @.(Koif[2] * Pt + Koif[1])
p2 = plot(Pt, Dt, lw=3, title="Зависимость Dt и Dmod от величины ВВП России(2010-2053 гг.)", xlabel=L"P_t млн.дол.США",
ylabel=L"D_t ,\;D_{mod} o.e.", lc=:red, label=L"D_t")
plot!(Pt, Dmod, lw=3, lc=:blue, label=L"D_{mod} \; получена\; на \;[0,10000]")
plot(p1, p2, layout=(2, 1), wsize=(800, 800), legend=true)
Из графиков видно, что зависимость экологической нагрузки от величины ВВП есть возрастающая функция, которая имеет точку P(2030)=10000 смены тенденций, т.е от 2010 г. до 2030 г. темп роста практически постоянный так как D(P) очень хорошо описывается линейной зависимостью и ,но в дальнейшем скорость роста экологической нагрузки резко возрастает, хотя и остается в сценарный период досточно далеко от
Интересно сравнить экологические нагрузки, которую может оказать экономика России при реализации сценария 7 (неустойчивое разрушающее развитие) и сценария 9 (устойчивое развитие). Для этого по данным глобальной модели Медоуза, скорректированной по ВВП для России построим модель для разрушительного сценария . Эта модель строится из предположения экспоненциального роста экологической нагрузки, параметры функции оценивались на основе аппроксимации откорректированных для России данных глобальной модели Медоуза.
Поделив функции и , на предельное значение, можно получить соответствующие относительные функции экологической нагрузки.
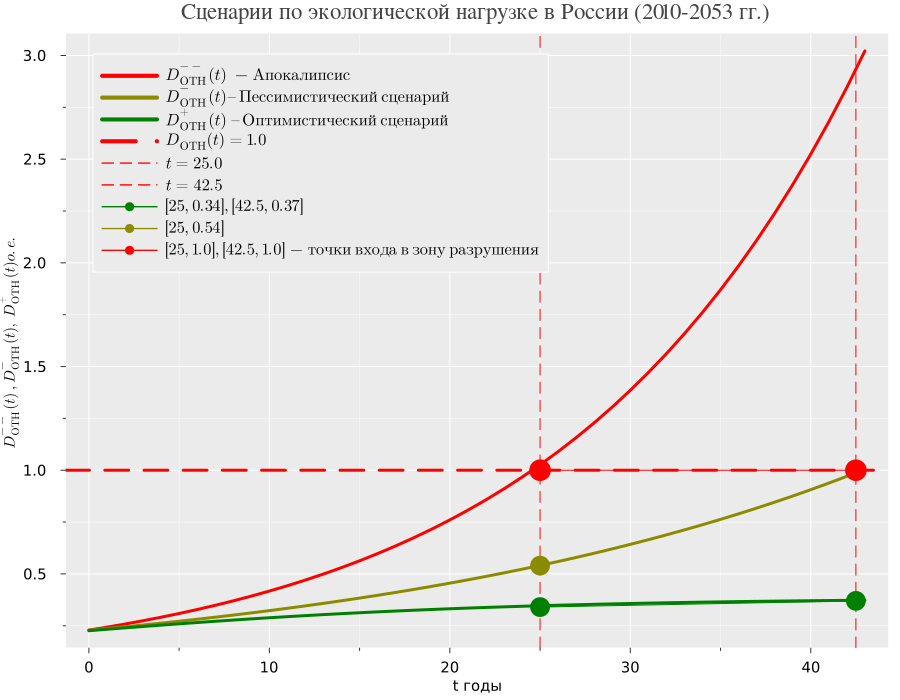
Для анализа поведения природного капитала в зоне разрушения введем в рассмотрение сценарий «Апокалипсис», в котором предельный уровень достигается через 25 лет. В результате получаем три относительных функции экологической нагрузки:
-
- предельно пессимистический сценарий;
-
- пессимистический сценарий;
-
- оптимистический сценарий.
Графически эти сценарии представлены ниже
using Plots, PlotThemes
using LaTeXStrings
using DataFrames, GLM, StatsBase
t = (0.0:1.0:43.0)
D1t = @.(0.229 * exp(0.06 * t))
D2t = @.(0.2289* exp(0.0344 * t))
D3t = @.(0.6329 * exp(0.075 * t) / (2.8 + 1.65 * (exp(0.075 * t) - 1)))
gr()
#plotly()
theme(:ggplot2)
#theme(:dao)
default(titlefont=(14, "times"), legendfontsize=11, guidefont=(10, :black), tickfont=(10, :black))
plot(t,D1t,lc=:red, lw=3.0,title="Сценарии по экологической нагрузке в России (2010-2053 гг.)",label=L"D_{ОТН}^{--}(t)\; - Апокалипсис")
plot!(t, D2t, lc=:yellow4, lw=3.0, xlabel="t годы", label=L"D_{ОТН}^{-}(t) –\; Пессимистический \;сценарий")
plot!(t, D3t, lc=:green, lw=3.0, ylabel=L"D_{ОТН}^{--}(t)\;,D_{ОТН}^{-}(t),\;D_{ОТН}^{+}(t) o.e.",
label=L"D_{ОТН}^{+}(t)\; – \;Оптимистический\; сценарий", wsize=(900, 700))
hline!([1.0], lw=3, lc=:red, linestyle=:dash, label=L"D_{ОТН}(t)=1.0")
vline!([25.0], lw=1, lc=:red, linestyle=:dash,label=L"t=25.0")
vline!([42.5], lw=1, lc=:red, linestyle=:dash, label=L"t=42.5")
plot!([25.0, 42.5], [0.34, 0.37], label=L"[25,0.34] ,[42.5,0.37]",
seriescolor=:green,
marker=:circle,
markersize=11,
markercolor=:green,
markerstrokecolor=:green
)
plot!([25.0], [0.54], label=L"[25,0.54]",
seriescolor=:yellow4,
marker=:circle,
markersize=11,
markercolor=:yellow4,
markerstrokecolor=:yellow4
)
plot!([25.0, 42.5], [1.0, 1.0], label=L"[25,1.0] ,[42.5,1.0]- точки\; входа\; в \;зону \;разрушения",
seriescolor=:red,
marker=:circle,
markersize=12,
markercolor=:red,
markerstrokecolor=:red
)
Из (8) имеем:
При этом ,
где
Для того что бы учесть естественную восстанавливающую силу природы введем коэффициент демпфирования вредного влияния экологической нагрузки на природный капитал АСЭЭС :
При восстанавливающая сила природы равна 0, а при она стремиться к некоторому предельному уровню. Вопрос состоит в том, как включить этот параметр в модель динамики и на основе, каких предположений оценивать:
-
Коэффициент демпфирования должен уменьшать падение уровня продуктивности земли в любой точке интервала , где - конечная точка сценария.
-
При уменьшении данного коэффициента функция должна смещаться вверх, но при этом оставаться отрицательной, что должно обеспечивать не возрастающий характер функции (природный капитал не может самовозрастать под антропогенной экологической нагрузкой)
-
В пространстве параметров должна существовать область (в предельном случае точка), в которой модель динамики обеспечивает выход в заданные временные диапазоны в зону разрушения природного капитала при соответствующих сценариях (сценарий 1 25-30 годы, сценарий 2 39-43 годы)
-
Должны существовать обеспечивающие в любой точке интервала выполнение условия:
Включение в , при котором выполняются приведенные выше условия, может быть выполнено следующими способами:
Для случая (а) можно записать:
Отсюда
то есть
Или для случая (б):
Таким образом, имея значение коэффициента демпфирования, можно оценивать положительную динамику влияния процессов самоочищения и самовосстановления природного капитала (см. ниже):
using Plots, PlotThemes
using LaTeXStrings
using DataFrames, GLM, StatsBase
m=1.45
apr=0.5
kdem=[0.5,0.7,0.9]
Dotn= (0.1:0.01:1.0)
#ColnN=['g','c','y']
Lb=[L"k_{dem}=0.5",L"k_{dem}=0.7",L"k_{dem}=0.9"]
gr()
#plotly()
#theme(:ggplot2)
theme(:dao)
default(titlefont=(14, "times"), legendfontsize=11, guidefont=(10, :black), tickfont=(10, :black))
p1=plot(xlabel=L"D_{otn}",ylabel=L"n^{N+}",title ="Вариант а)")
for i in 1:3
at=@.(-apr*Dotn^m+1)
k_ek = @.((1 / at)*(1 - kdem[i]))
plot!(Dotn,k_ek, lw=3.0,label=Lb[i])
end
annotate!([0.4], [0.92], [text(L"m=1.45", :black, 14)])
annotate!([0.4], [0.85], [text(L"a^{pr}=0.5", :black, 14)])
p2 = plot(xlabel=L"D_{otn}", ylabel=L"n^{N+}", title="Вариант б)")
for i in 1:3
at = @.(-apr * Dotn^m + 1)
k_ek =@.(1/at-(1/(-apr*kdem[i]*Dotn^m+1)))
plot!(Dotn,k_ek, lw=3.0,label=Lb[i])
end
annotate!([0.4], [0.58], [text(L"m=1.45", :black, 14)])
annotate!([0.4], [0.53], [text(L"a^{pr}=0.5", :black, 14)])
plot(p1, p2, layout=(2, 1), wsize=(800, 800), legend=true)
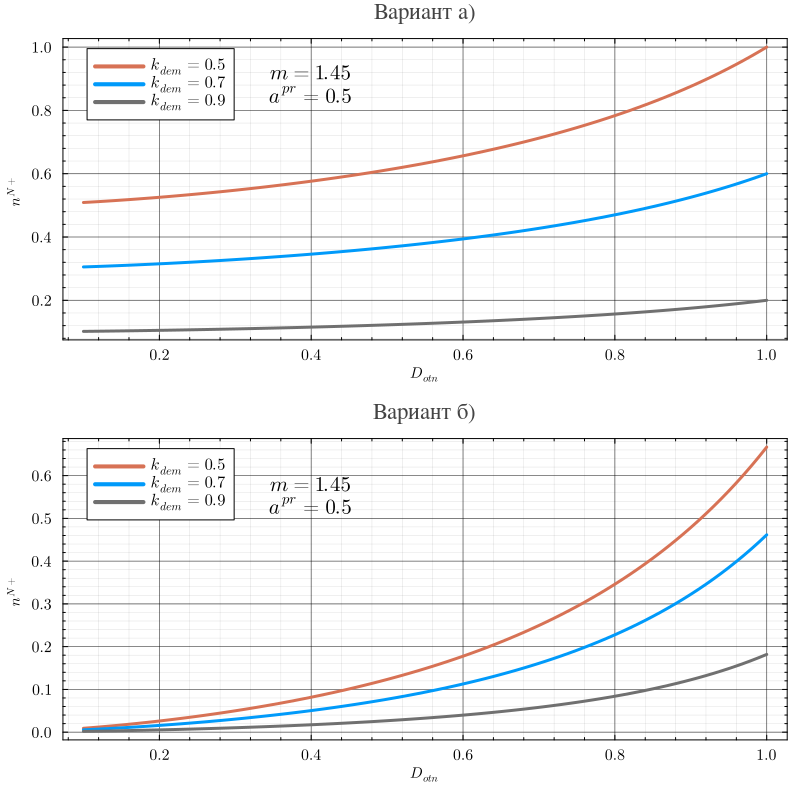
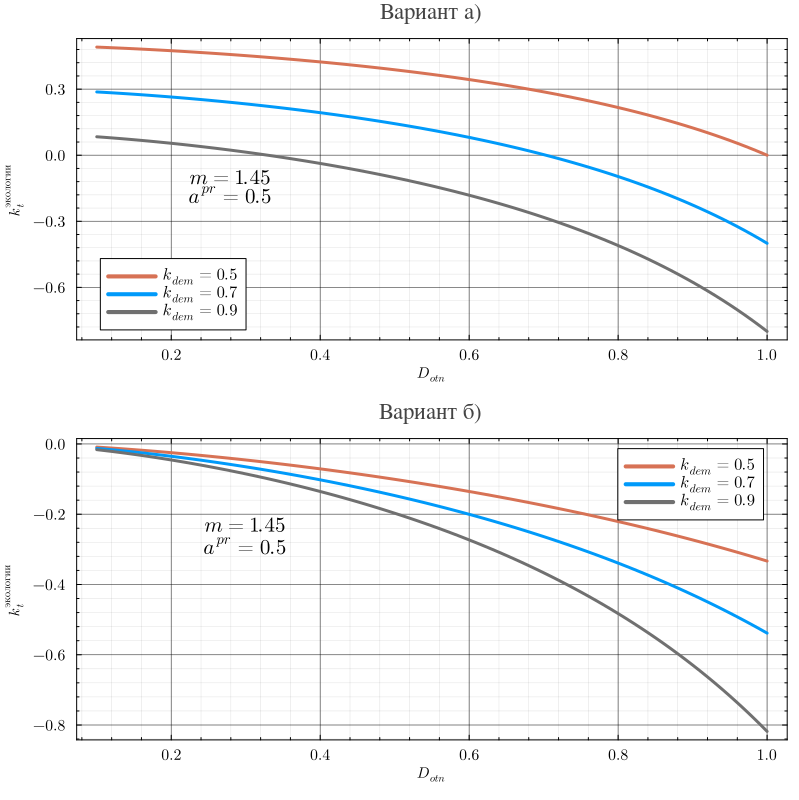
Графики функций для вариантов и представлены ниже:
using Plots, PlotThemes
using LaTeXStrings
using DataFrames, GLM, StatsBase
m = 1.45
apr = 0.5
kdem = [0.5, 0.7, 0.9]
Dotn = (0.1:0.01:1.0)
#ColnN=['g','c','y']
Lb = [L"k_{dem}=0.5", L"k_{dem}=0.7", L"k_{dem}=0.9"]
gr()
#plotly()
#theme(:ggplot2)
theme(:dao)
default(titlefont=(14, "times"), legendfontsize=11, guidefont=(10, :black), tickfont=(10, :black))
p1 = plot(xlabel=L"D_{otn}", ylabel=L"k_t^{экологии}", title="Вариант а)")
for i in 1:3
at = @.(-apr * Dotn^m + 1)
k_ek = @.(1- kdem[i]/at)
plot!(Dotn, k_ek, lw=3.0, label=Lb[i])
end
annotate!([0.28], [-0.1], [text(L"m=1.45", :black, 14)])
annotate!([0.28], [-0.18], [text(L"a^{pr}=0.5", :black, 14)])
p2 = plot(xlabel=L"D_{otn}", ylabel=L"k_t^{экологии}", title="Вариант б)")
for i in 1:3
at = @.(-apr * Dotn^m + 1)
k_ek = @.(1 - (1 / (-apr * kdem[i] * Dotn^m + 1)))
plot!(Dotn, k_ek, lw=3.0, label=Lb[i])
end
annotate!([0.3], [-0.23], [text(L"m=1.45", :black, 14)])
annotate!([0.3], [-0.29], [text(L"a^{pr}=0.5", :black, 14)])
plot(p1, p2, layout=(2, 1), wsize=(800, 800), legend=true)
Варианты (а) и (б) демонстрируют две разные «стратегии» природы во взаимоотношении с человеком. При слабой величине восстановительной силы природы в обоих вариантах вблизи предельной нагрузки имеет близкие значения, то есть в варианте (б) реализуется в данной области значительно более высокий темп роста при повышении экологической нагрузки. В интервале различия в темпе роста сначала снижаются, а при варианты (а) и (б) начинают показывать практически одинаковые темпы роста .
Но при этом быстро растет различие в начальном значении в результате для разница в значениях около предельной нагрузки достигает различия несколько раз в пользу варианта (б). Таким образом, вариант (б) обеспечивает имитацию более мощного позитивного воздействия природы особенно в условиях высокой экологической нагрузки.
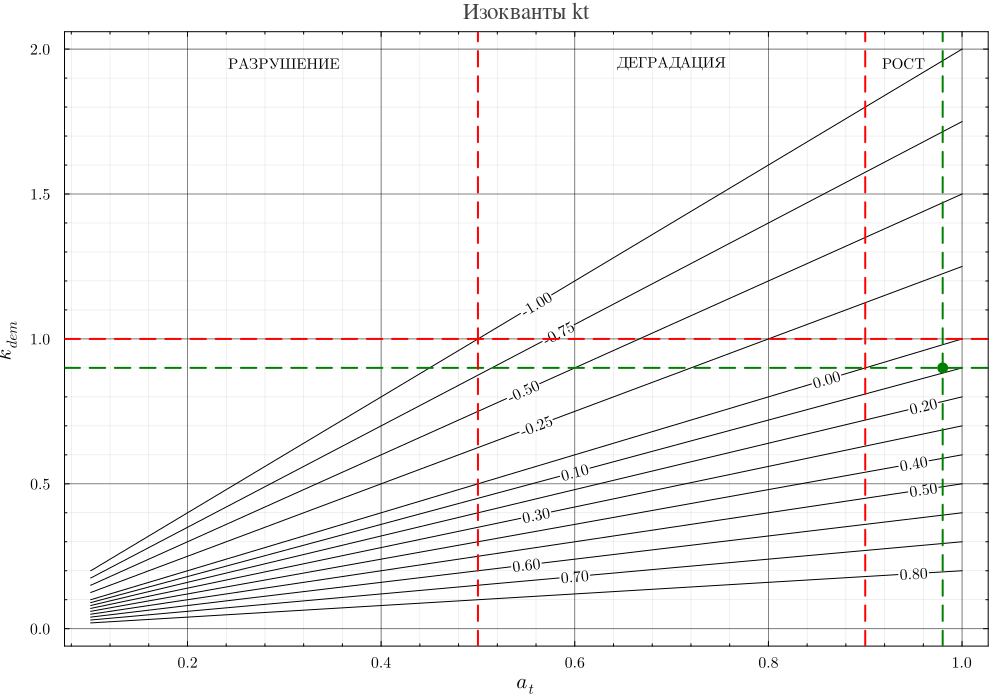
Если говорить об условиях сформулированных выше, то для варианта (б) условия 1 и 2 выполнятся вполне очевидно, для варианта (а) условие 1 выполняется в силу того, что уменьшение числителя в дроби выражения (13) тождественно увеличению знаменателя в этом же выражении, а это эквивалентно росту продуктивности земли. Условие 2 для варианта (а) требует специального анализа. Построим в системе координат изокванты для которых выполняются условия:
using Plots, PlotThemes
using LaTeXStrings
kdem = (0.0:0.01:2.0)
at = (0.1:0.01:1.0)
lev = [-1.0, -0.75, -0.5, -0.25, 0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 1.0]
#lev1=[-1.0, -0.75, -0.5, -0.25]
#lev2=[0.0]
#lev3 = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 1.0]
gr()
#plotly()
#theme(:ggplot2)
theme(:dao)
default(titlefont=(14, "times"), legendfontsize=11, guidefont=(14, :black), tickfont=(10, :black))
kt=zeros(201, 91)
for i in 1:201
for j in 1:91
kt[i,j]=1 - (kdem[i] /at[j])
end
end
#contour(at, kdem, kt, levels=lev1, lw=1.0, contour_labels=true, lc=:red)
#contour!(at, kdem, kt, levels=lev2, lw=1.0, contour_labels=true, lc=:black)
#contour!(at, kdem, kt, levels=lev3, lw=1.0, contour_labels=true, lc=:green)
plot(title="Изокванты kt", xlabel=L"a_t", ylabel=L"k_{dem}", wsize=(1000, 700), legend=false)
contour!(at, kdem, kt, levels=lev, lw=1.0, contour_labels=true, lc=:black)
hline!([1.0], lw=2, lc=:red, linestyle=:dash,labels=false)
hline!([0.9], lw=2, lc=:green, linestyle=:dash, labels=false)
vline!([0.5], lw=2, lc=:red, linestyle=:dash, labels=false)
vline!([0.9], lw=2, lc=:red, linestyle=:dash, labels=false)
vline!([0.98], lw=2, lc=:green, linestyle=:dash, labels=false)
annotate!([0.3], [1.95], [text(L"РАЗРУШЕНИЕ", :black, 10)])
annotate!([0.7], [1.95], [text(L"ДЕГРАДАЦИЯ", :black, 10)])
annotate!([0.94], [1.95], [text(L"РОСТ", :black, 10)])
plot!([0.98], [0.9],label=false,
seriescolor=:green,
marker=:circle,
markersize=6,
markercolor=:green,
markerstrokecolor=:green
)
using Plots, PlotThemes
using LaTeXStrings
kdem = (0.0:0.01:2.0)
at = (0.1:0.01:1.0)
lev = [-1.0, -0.75, -0.5, -0.25, 0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 1.0]
plotly()
theme(:dao)
kt = zeros(201, 91)
for i in 1:201
for j in 1:91
kt[i, j] = 1 - (kdem[i] / at[j])
end
end
my_cg = cgrad([:blue, :red, :orange, :yellow]);
surface(at, kdem, kt, title="Коэффициент экологии kt", c=my_cg, wsize=(900, 800),legend = false)
xlabel!("at")
ylabel!("kdem")
contourf(at, kdem, kt, levels=range(-18.0, stop=1.0, length=100), cbar=true, wsize=(600, 600),title = "Изокванты kt ")
Из графика видно, что только при во всем диапазоне изменения обеспечивается отрицательные значения - движение по изоквантам от нулевой до больших отрицательных. При уменьшении появляются области значений , где принимает положительные значения. Поэтому целесообразно выбирать уровень начальной антропогенной нагрузки отличным от нуля и тогда находя точку пересечения этого значения с нулевой изоквантой определяем нижнюю границу интервала значений в котором выполняется условие 2.
Учитывая выше приведенные рассуждения и воспользовавшись выражением (5) получаем основное уравнение динамики природного капитала (без природо-восстановительной деятельности человека):
Задавая различные значения коэффициента демпфирования, а также и можно изучать поведение системы при разных сценариях развития экологической ситуации в АСЭЭС и разных гипотезах влияния экологии на динамику природного капитала.
Используемые в динамической модели, как константы, параметры, безусловно, являются сложными функциями, изменения которых во времени связаны с фундаментальными законами природы, формулируемыми экологией, биологией, почвоведением, агрохимией и другими естественными науками.
Здесь еще много неизвестного, но ряд уже полученных результатов позволяет формулировать гипотезы о динамике адаптационных свойств природы. При этом изучение влияния предложенных параметров на динамику природного капитала позволяет проверять уже имеющиеся и выдвигать дополнительные гипотезы о механизмах взаимовлиянии человека и природы.
Располагая основной динамической моделью, можно перейти к моделированию динамики природного капитала. Но предварительно введем формальное определение понятий разрушение природного капитала АСЭЭС и точки разрушения.
Природный капитал разрушился в момент , если выполняется условие:
где - бесконечно малая положительная величина;
- момент разрушения (точка разрушения).
При выполнении условия (18) происходит абсолютное (тотальное) разрушение. Можно ввести понятие относительного разрушения на определенном уровне:
где - уровень разрушения, задаваемый, например, как определенный процент ;
- момент времени, в который выполняется условие (19) .
Теперь перейдем к модельным экспериментам для этого решаем дифференциальное уравнение (17) при разных комбинациях параметров для всех трех сценариев, добиваясь сформулированных выше условий.
Используя «вариант а» включения в модель, мы получили решение дифференциального уравнения (17) на диапазоне при начальных условия млн.га. Это площадь сельхозугодий России в 2009 году (Росстат, статистический сборник «Россия и страны мира 2010»). Решения в основном соотвествуют сформулированным выше условиям и получены при следующих значениях параметров , ,
#=Модель трансформации природного капитала АПК
1. Позитивное воздейcтвие человека отсутствует
2. Рассматривается первая "стратегия природы"- случай а)
3. Рассматриваются все три функции относительной экологической нагрузки Dотн(t)=#
#первый сценарий развития природного капитала АПК РФ
using DifferentialEquations, Plots, PlotThemes
function fN1!(du, u, p, t)
D_otn11 = 0.229 * exp(0.06 * t)
at1 = -(a_pr * D_otn11^m) + 1
w = (1 - (kdem / (at1)))
du[1] = u[1] * w
end
#ВХОДНЫЕ ПАРАМЕТРЫ
tn = 25.0 #Конец сценария 1
a_pr = 0.5
m = 1.45
kdem = 0.9
N0 = 221.0
tspan = (0.0, tn)
u0 = [N0]
p = (a_pr, m, kdem)
prob = ODEProblem(fN1!, u0, tspan, p)
sol = solve(prob, abstol=1e-8, reltol=1e-8);
TN1 = deepcopy(sol.t)
FN1 = deepcopy(sol.u)
FN1 = reduce(vcat, FN1);
#второй сценарий развития природного капитала АПК РФ
function fN2!(du, u, p, t)
D_otn12 = 0.2289 * exp(0.0344 * t)
at2 = -(a_pr * D_otn12^m) + 1
w = (1 - (kdem / (at2)))
du[1] = u[1] * w
end
N0 = 221.0
tn = 43.0 #Конец сценария 2
tspan = (0.0, tn)
u0 = [N0]
p = (a_pr, m, kdem)
prob = ODEProblem(fN2!, u0, tspan, p)
sol = solve(prob, abstol=1e-8, reltol=1e-8);
TN2 = deepcopy(sol.t)
FN2 = deepcopy(sol.u)
FN2 = reduce(vcat, FN2);
#третий сценарий развития природного капитала АПК РФ
function fN3!(du, u, p, t)
D_otn13 = (0.6329 * exp(0.075 * t)) / (2.8 + 1.165 * (-1 + exp(0.075 * t)))
at3 = -(a_pr * D_otn13^m) + 1
w = (1 - (kdem / (at3)))
du[1] = u[1] * w
end
N0 = 221.0
tn = 43.0 #Конец сценария 3
tspan = (0.0, tn)
u0 = [N0]
p = (a_pr, m, kdem)
prob = ODEProblem(fN3!, u0, tspan, p)
sol = solve(prob, abstol=1e-8, reltol=1e-8)
TN3 = deepcopy(sol.t)
FN3 = deepcopy(sol.u)
FN3 = reduce(vcat, FN3);
gr()
theme(:dao)
default(titlefont=(12, "times"), legendfontsize=10, guidefont=(12, :black), tickfont=(10, :black))
plot(TN1, FN1, title="Сценарии развития N в отсутствии инвестиций\n (первая стратегия природы-случай а)", ylabel="N млн.га", xlabel="t", lw=2, linecolor=:red, label="Сценарий 1",
wsize=(950, 700), legend=:outertopright)
plot!(TN2, FN2, lw=2, linecolor=:5, label="Сценарий 2")
plot!(TN3, FN3, lw=3, linecolor=:green, label="Сценарий 3")
hline!([N0 * 0.1], lw=2, lc=:red, linestyle=:dash, label="Граница зоны\n разрушения N")

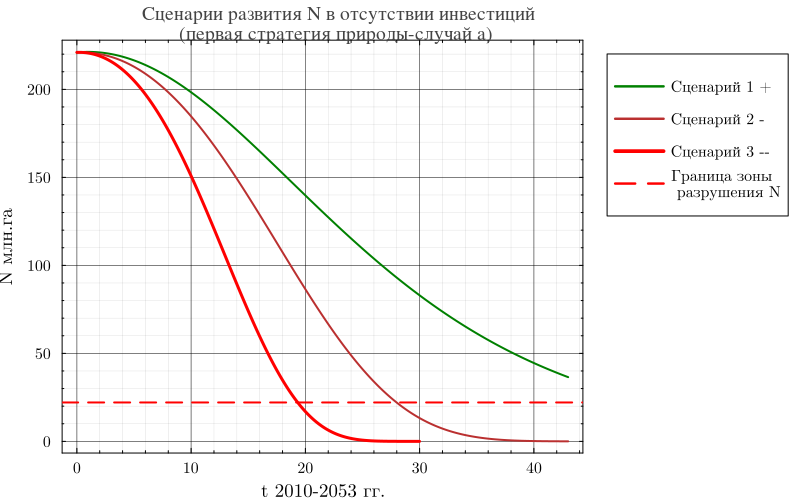
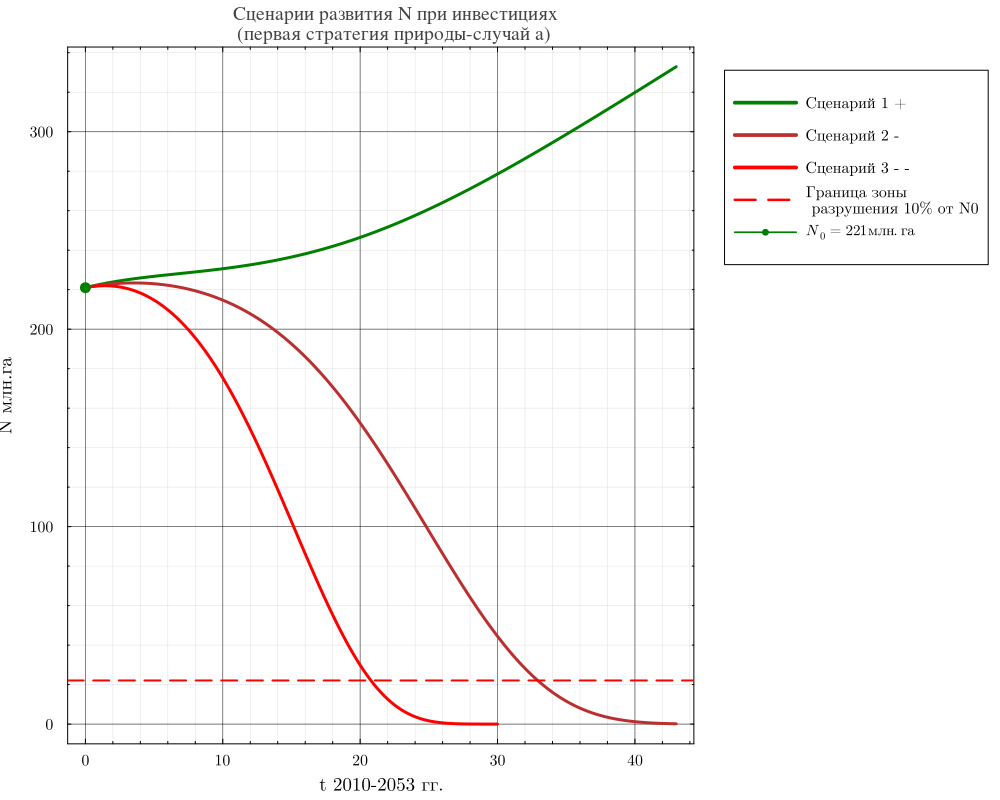
График показывает следующие результаты. При первой «стратегии» природы (вариант а) можно ожидать, что к t=22 по сценарию 1 потери природного капитала АСЭЭС России достигнут болеее 90 процентов и система войдет в зону 10 процентного разрушения.По второму сценарию система войдет в зону разрушения природного капитала к t=34, а по третьему на конец сценареого периода t=43 уровень природного капитала составит 32.15 млн. га.При этом даже по первому сценарию первые 7 лет наблюдается рост до 250.8 млн.га, а затем начинается ускоряющися спад. По второму и третьему сценариям рост идет до 285.0 млн.га при t=11 и 280.44 млн.га при t=10 соотвественно.То есть до t=17 второй сценарий показывает себя немного лучше, чем третий.Дальше второй сценарий показывает гораздо более быстрое снижение природного капитала системы по сравнению с третьем сценарием.Полное разрушение природного капитала по сценарию 1 наступает примерно в точке t=26 остаточный уровень меньше 0.01 процента от N(0), если анализировать ситуацию дальше, то в точке приблизительно t=29 система попадает в отрицательную зону и переходит в затухающий колебательный режим.
Важно оценить, как изменяется решение от значения k_dem . На рисунке ниже показаны решения дифференциального уравнения (17)при значениях , когда позитивная роль природы отсутствует до почти предельного позитивного значения . Из рисунка видно, что дифференциация решений в зоне относительно небольшая. Затем при разброс решений увеличивается и происходит изменения вида функции от вогнутой вниз к вогнутой вверх. Это означает, что темпы (скорость) падения природного капитала меняет характер от снижающихся во времени до возрастающих.
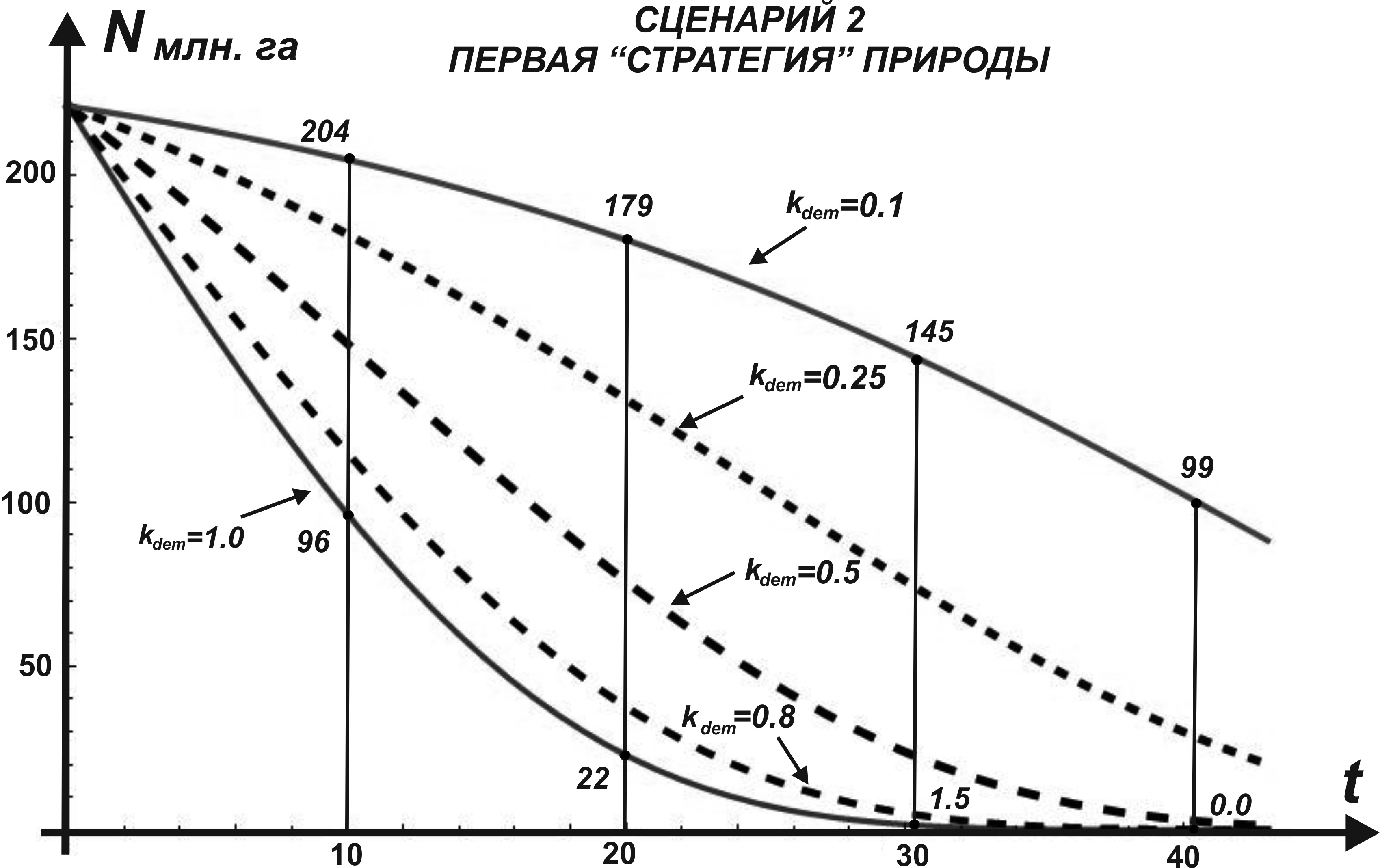
Рассмотрим поведение при третьем сценарии. Здесь картина очень интересная.При значении имеется точка бифуркации. В этой точке происходит смена тенденций в изменении N(t) на интервале от падения к стабилизации, а затем к росту. При стабилизируется т.е. природа полностью компенсирует отрицательное антропогенное воздействие, оказываемое по стратегии 3. При наступает режим постоянного почти линейного роста, а дальше при падении система срывается в положительный коллапс. При система переходит в режим первоначального роста, затем падения природного капитала до уровня разрушения.При система входит по сценарию 3 в режим постоянного падения и смещения точки входа в зону разрушения влево. При = 1.0 (восстанавливающая сила природы отсутствует) система будет разрушена по всем трем сценариям при .
Таким образом, данная «стратегия» природы характеризуется высоким уровнем чувствительности к объему экологической нагрузки и величине и направлению скорости ее изменения
Априорные соображения, положенные в основу сценариев 2 и 3, дают возможность предполагать, что наиболее вероятной областью значений коэффициента демпфирования, при первой стратегии природы, является интервал (0.9,0.95].
Перейдем к решению дифференциального уравнения (17) при второй стратегии природы (случай б включения в модель). Решения для следующего набора параметров , представлены графически (см.ниже).
#=Модель трансформации природного капитала АПК
#1. Позитивное воздейcтвие человека отсутствует
#2. Рассматривается вторая "стратегия природы"- случай б)
#3. Рассматриваются все три функции относительной экологической нагрузки Dотн(t)=#
#--------решение дифференциальных уравнений 17----------------------------
#---АПОКАЛИПСИС i=1 ------------------------------------------------------
using DifferentialEquations, Plots, PlotThemes
function f2N1!(du, u, p, t)
D_otn21 = 0.229 * exp(0.06 * t)
w = (1 - (1/(1-a_pr*kdem*D_otn21^m)))
du[1] = u[1] * w
end
#=ВХОДНЫЕ ПАРАМЕТРЫ=#
tn = 43 #Конец сценария
a_pr=0.5
m =1.45
kdem =0.3
N0 = 221
tspan = (0.0, tn)
u0 = [N0]
p = (a_pr, m, kdem)
prob = ODEProblem(f2N1!, u0, tspan, p)
sol = solve(prob, abstol=1e-8, reltol=1e-8);
TN1 = deepcopy(sol.t)
FN1 = deepcopy(sol.u)
FN1 = reduce(vcat, FN1);
#--------------ПЛОХОЙ СЦЕНАРИЙ i=2--------------------------------------------
function f2N2!(du, u, p, t)
D_otn22 = (0.2289*exp(0.0344*t))
w = (1 - (1/(1-a_pr*kdem*D_otn22^m)))
du[1] = u[1] * w
end
prob2 = ODEProblem(f2N2!, u0, tspan, p)
sol2 = solve(prob2, abstol=1e-8, reltol=1e-8);
TN2 = deepcopy(sol2.t)
FN2 = deepcopy(sol2.u)
FN2 = reduce(vcat, FN2);
#--------------ХОРОШИЙ СЦЕНАРИЙ i=3--------------------------------------------
function f2N3!(du, u, p, t)
D_otn23 = ((0.6329*exp(0.075*t))/(2.8+1.165*(-1+exp(0.075*t))))
w = (1 - (1/(1-a_pr*kdem*D_otn23^m)))
du[1] = u[1] * w
end
prob3 = ODEProblem(f2N3!, u0, tspan, p)
sol3 = solve(prob3, abstol=1e-8, reltol=1e-8);
TN3 = deepcopy(sol3.t)
FN3 = deepcopy(sol3.u)
FN3 = reduce(vcat, FN3);
#----------------ПОСТРОЕНИЕ ГРАФИКОВ--------------
theme(:dao)
default(titlefont=(14, "times"), legendfontsize=10, guidefont=(12, :black), tickfont=(10, :black))
plot(TN1, FN1, title="Сценарии развития N в отсутствии инвестиций\n (вторая стратегия природы-случай б)", ylabel="N млн.га", xlabel="t", lw=2, linecolor=:red, label="Сценарий 1",
wsize=(950, 700), legend=:outertopright)
plot!(TN2, FN2, lw=2, linecolor=:5, label="Сценарий 2")
plot!(TN3, FN3, lw=3, linecolor=:green, label="Сценарий 3")
hline!([N0 * 0.1], lw=2, lc=:red, linestyle=:dash, label="Граница зоны\n разрушения N")
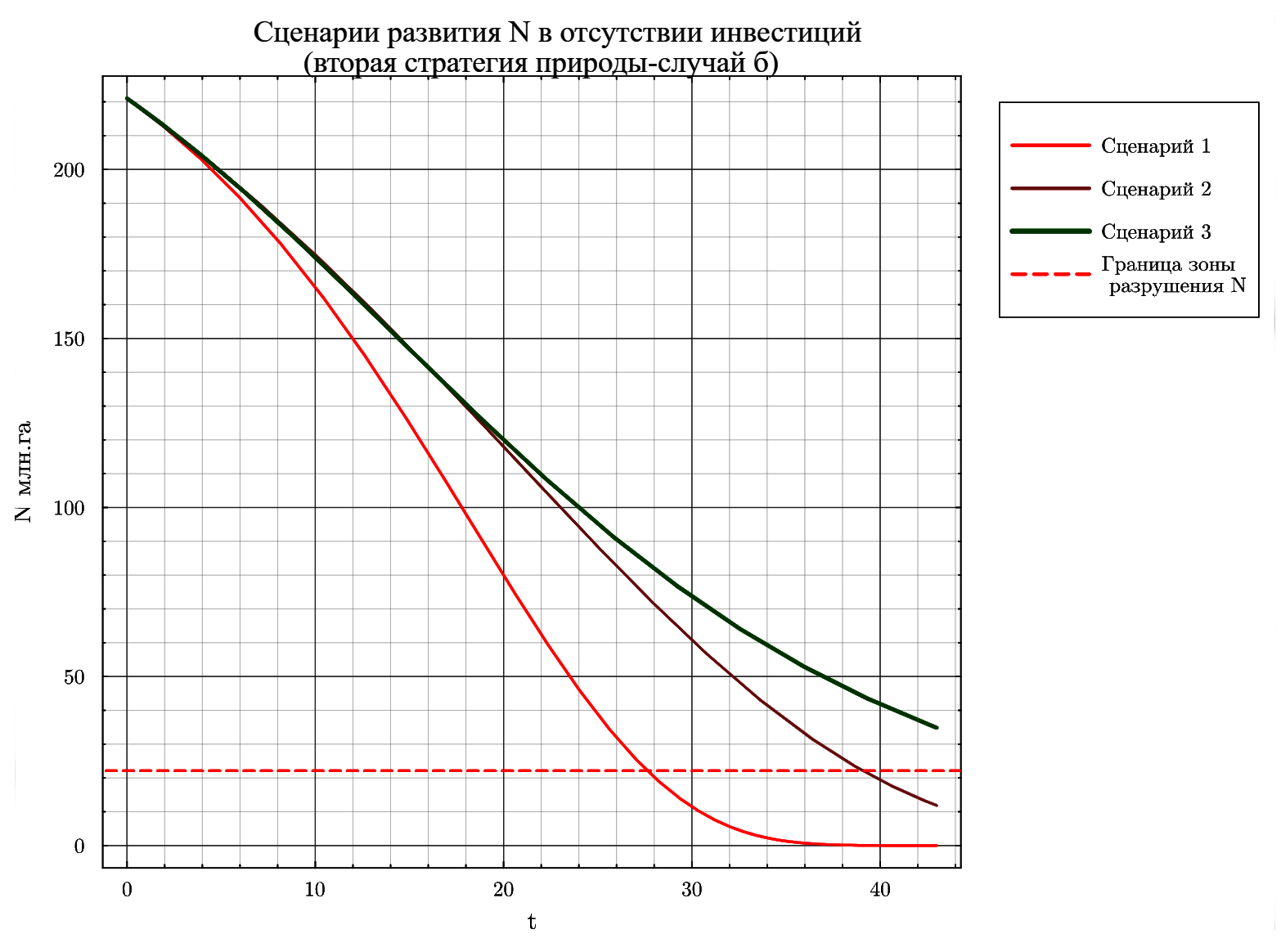
Решения выглядят несколько иначе, чем в первом случае. Природа более слабо реагирует на незначительную негативную экологическую нагрузку (интервал [0,20]), причем тем слабее, чем ниже скорость ее возрастания. В силу этого сценарий 3 демонстрирует совершенно другой характер , чем в первом случае. Он значительно приближается к сценариям 1 и 2. При увеличении экологической нагрузки позитивная роль природы возрастает в результате точки разрушения в сценариях 1 и 2 немного смещаются к концу интервала [0,43], но остаются в зоне априорных соображений.
Посмотрим, как влияет значение значения на решение при этой стратегии природы.Результаты решения дифференциального уравнения (17) при разных значениях для сценариев 1, 2 и 3 позволяют сделать следующие выводы.
При небольших значениях 0.05, 0.1,0,2 сценарии 2,3 демонстрируют высокую стабильность (спад N(t) порядка 20 процентов от начального уровня) и незначительные различия для t от 0 до 25-30.Сценарий 3 начинает выигравать у сценария 2 при t>25-30 и тем больше , чем больше .При только сценарий 3 не достигает при зоны разрушения.При востановительные силы природы не в состоянии компенсировать негативное влияние человека и в сценарий 3 демонстрирует переход системы в зону разрушения. При значениях начинается полное разрушение системы, сначало для сценария 1(здесь система уже полностью разрушалась приблизительно при ) затем для сценария 2, затем почти полностью разрушается система и при сценарии 3.
Если сравнить решения для одноименных сценариев при разных стратегиях природы при разных , то можно констатировать:
-
при второй "стратегии" поведение в сценариях 2 и 3 относительно мало отличаются друг от друга при разных ;
-
при первой "стратегии" поведение сценарии 2,3 при разных отличаются друг от друга кардинально
Природа при первой «стратегии» реагирует на негативноеное поведение человека особенно при малых экологических нагрузках на порядок сильнее в положительном направлении, чем при второй "стратегии".
Таким образом, вторая «стратегия природы» отличается значительной робастностью к изменению сценария поведения человека. Включение в модель той или иной «стратегии природы» определяется дополнительной априорной информацией о эколого-экономических закономерностях взаимодействия человека и природы. Кроме того, видимо, целесообразно учитывать в модели позитивное влияние природы не как константу, а как некоторую функцию .
До сих пор мы рассматривали негативное влияние деятельности человека на природный капитал АСЭЭС и то, как природа может противодействовать этому. Перейдем к вопросам описаний позитивной природо-восстанавливающей деятельности человека в аграрной сфере
Рассмотрим следующее дифференциальное уравнение:
То есть, прирост природного капитала, есть от растущая функция от вложенных в его развитие инвестиций и их инновационности. При этом считаем, что прирост определяется ростом продуктивности 1 га земли, тогда аналогично тому как мы описывали падение природного капитала при росте продуктивности, имеем:
Величина , определяющая продуктивность земли в любой момент времени, зависит от величины инвестиций на 1 га земли и уровня их инновационности.
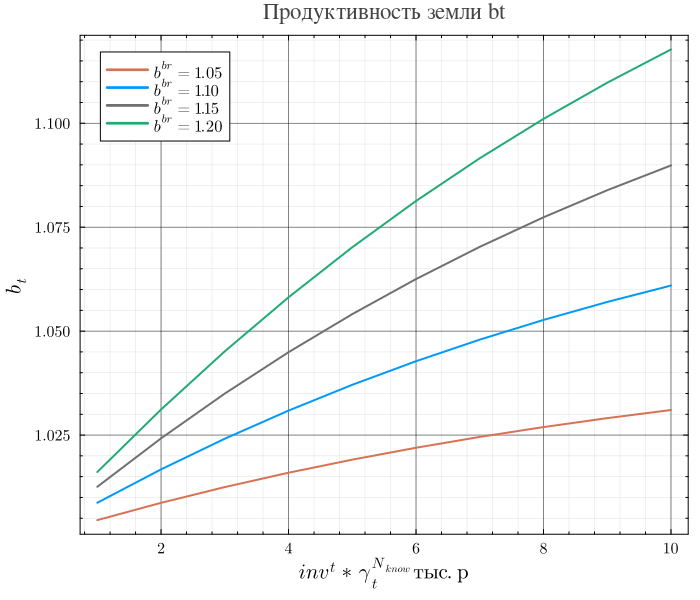
Коэффициент роста продуктивности земли из естественных соображений представляет собой монотонно возрастающую функцию произведения
область значений которой интервал .При этом в отсутствии инвестиций он должен принимать значение равное 1 , а значение , определяющее максимальный темп прироста природного капитала АСЭЭС, при предельно возможном объеме инвестиций и уровне их инновационности. Величина увеличивает, или уменьшают объем инвестиций, что либо увеличивает темп роста продуктивности земли либо снижает.
Можно предложить следующие модели роста продуктивности земли от уровня инвестиций:
using Plots, PlotThemes
using LaTeXStrings
b_br=[1.05,1.10,1.15,1.20]
inv_gam = (1.0: 1.0: 10.0)
#Colbbr=['g','c','y','coral']
Lb=[L"b^{br}=1.05",L"b^{br}=1.10",L"b^{br}=1.15",L"b^{br}=1.20"]
gr()
#plotly()
#theme(:ggplot2)
theme(:dao)
default(titlefont=(14, "times"), legendfontsize=11, guidefont=(14, :black), tickfont=(10, :black))
plot(title="Продуктивность земли bt", legend=:topleft)
for i in 1:4
bt=@.((b_br[i]*exp(0.1*inv_gam))/(b_br[i]+1.0*(exp(0.1*inv_gam))-1))
plot!(inv_gam ,bt,lw=2.0,label=Lb[i])
end
plot!(xlabel=L"inv^t*γ_t^{N_{know}} тыс.р", ylabel=L"b_t",wsize=(700, 600))
Зависимость от и графически может быть представлена следующим образом:
#ГРАФИК КОЭФФИЦИЕНТА ТЕМПОВ РОСТА ПРОДУКТИВНОСТИ ЗЕМЛИ
#В ПРОСТРАНСТВЕ ИНВЕСТИЦИЙ И ИННОВАЦИЙ
using Plots, PlotThemes
using LaTeXStrings
b_br = 1.15
Inv = (1.0:0.5:10.0)
γ = (0.1:0.1:2.0)
bt = zeros(19, 20)
for i in 1:19
for j in 1:20
bt[i, j] = (b_br * exp(0.1 * Inv[i] * γ[j])) / (b_br + 1.0 * (exp(0.1 * Inv[i] * γ[j])) - 1)
end
end
#gr()
plotly()
#theme(:ggplot2)
theme(:dao)
default(titlefont=(18, "times"), legendfontsize=11, guidefont=(18, :black), tickfont=(10, :black))
my_cg = cgrad([:blue, :red, :orange, :yellow]);
surface(Inv, γ, bt, title="Коэффицент темпов роста продуктивности земли-bt", c=my_cg, wsize=(900, 800), legend=true)
xlabel!("Invt")
ylabel!("γt")
zlabel!("bt o.e.")
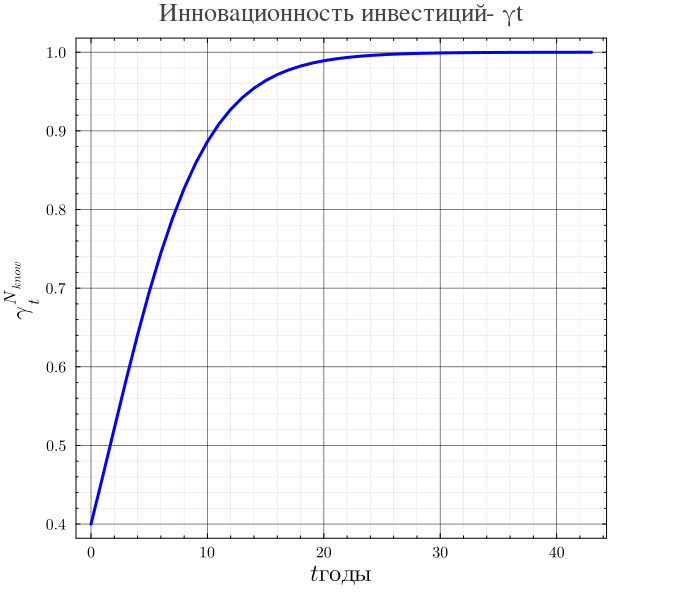
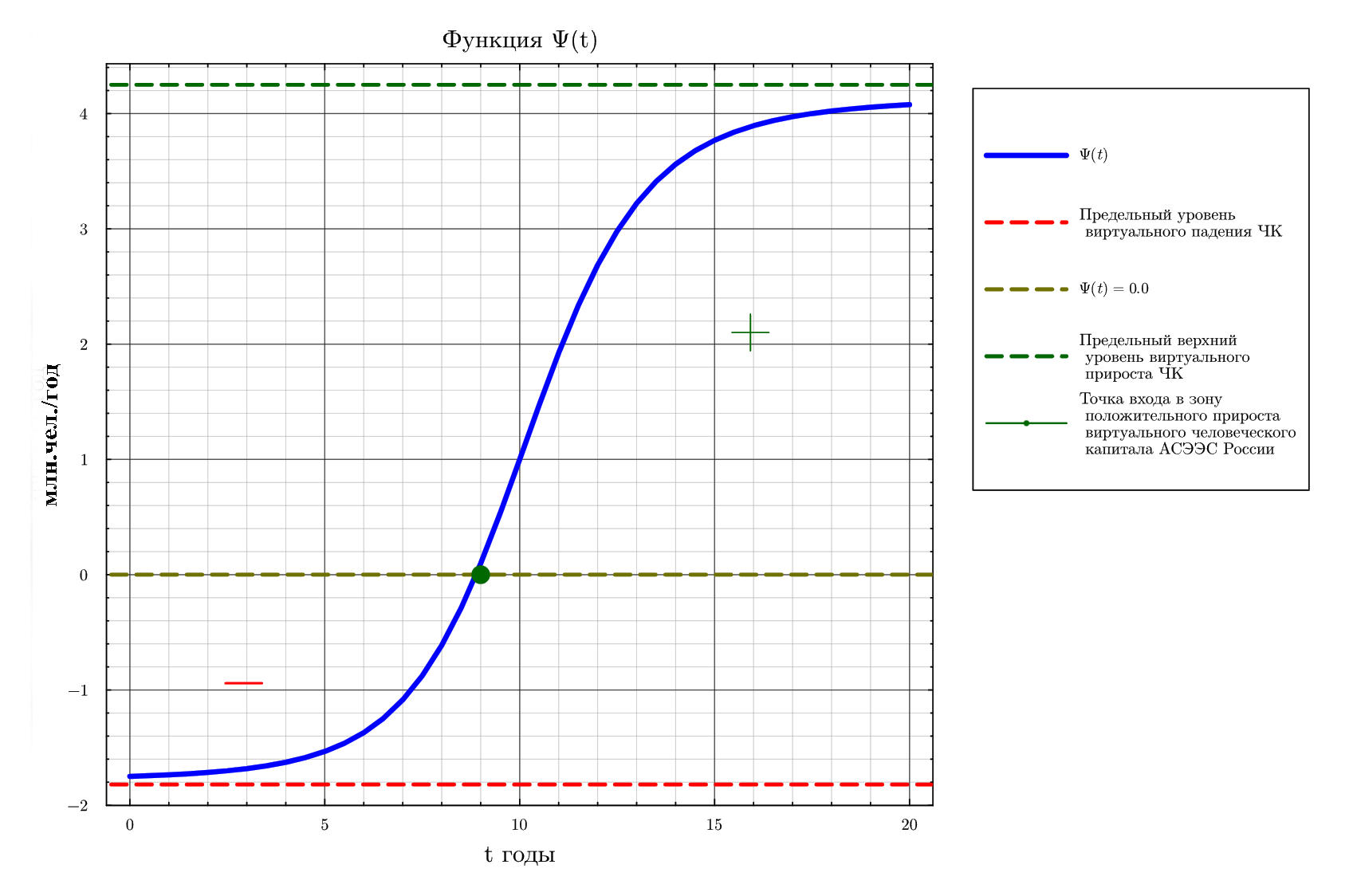
Уровень инновационности инвестиций, можно представить как монотонно возрастающую функцию времени, область значений которой представляет собой интервал , где предельно допустимый низший уровень инновационности инвестиций, а предельно возможный на интервале исследования высший уровень инновационности. Как и для других факторов развития при имеет место общественно необходимый уровень (средний уровень развитых экономик). Для демонстрации возможностей предлагаемого подхода возьмем следующую функцию:
using Plots, PlotThemes
using LaTeXStrings
t = (0.0:1.0:43.0)
γt = @.(0.4 * exp(0.246 * t) / (1.0 + 0.4 * (exp(0.246 * t) - 1)))
gr()
#plotly()
#theme(:ggplot2)
theme(:dao)
default(titlefont=(16, "times"), legendfontsize=11, guidefont=(16, :black), tickfont=(10, :black))
plot(t, γt, lw=3, title="Инновационность инвестиций- γt", xlabel=L"t годы", ylabel=L"γ_t^{N_{know}}", lc=:blue, label=false,
wsize=(700, 600))
Экономический смысл графика следующий. На начало сценарного времени инновационность инвестиций в природный капитал АСЭЭС России составляет порядка 40 процентов от общественно необходимого уровня (уровень развитых стран) предполагается, что приблизительно через 20 лет Россия достигнет 100 процентного уровня и будет поддерживать его до конца сценарного срока.
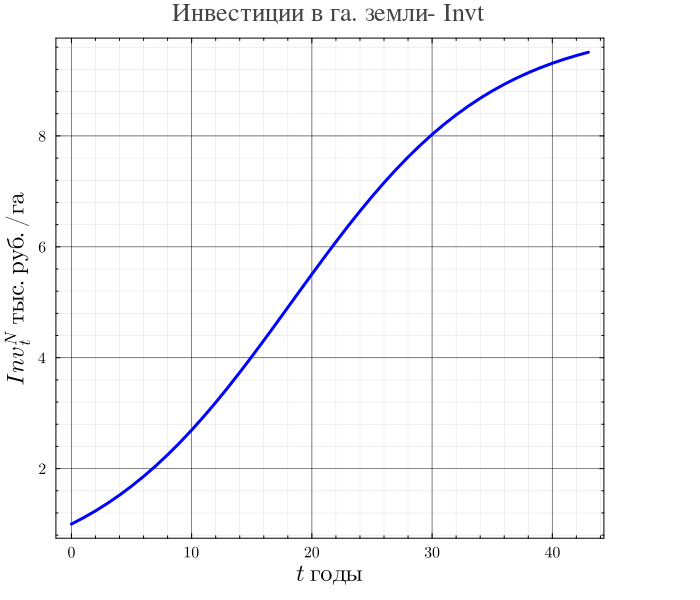
Важнейшей составляющей является модель инвестиций. Предполагается, что инвестиции на 1 га земли в повышение ее продуктивности есть монотонно возрастающая функция времени с областью значений . Для демонстрации возможностей подхода принимаем т.р/га , а =10 т.р/га, стратегию роста инвестиций в сценарный период представим в виде S-образной функции:
using Plots, PlotThemes
using LaTeXStrings
t = (0.0:1.0:43.0)
Invt = @.(10 * exp(0.12 * t) / (10 + 1.0 * (exp(0.12 * t) - 1)))
gr()
#plotly()
#theme(:ggplot2)
theme(:dao)
default(titlefont=(16, "times"), legendfontsize=11, guidefont=(16, :black), tickfont=(10, :black))
plot(t, Invt, lw=3, title="Инвестиции в га. земли- Invt", xlabel=L"t\; годы", ylabel=L"Inv_t^{N} \;тыс.руб./га", lc=:blue, label=false,
wsize=(700, 600))
Таким образом, располагая построенными выше соотношениями, после несложных преобразований мы приходим к следующему дифференциально-му уравнению, описывающему динамику роста природного капитала АСЭЭС:
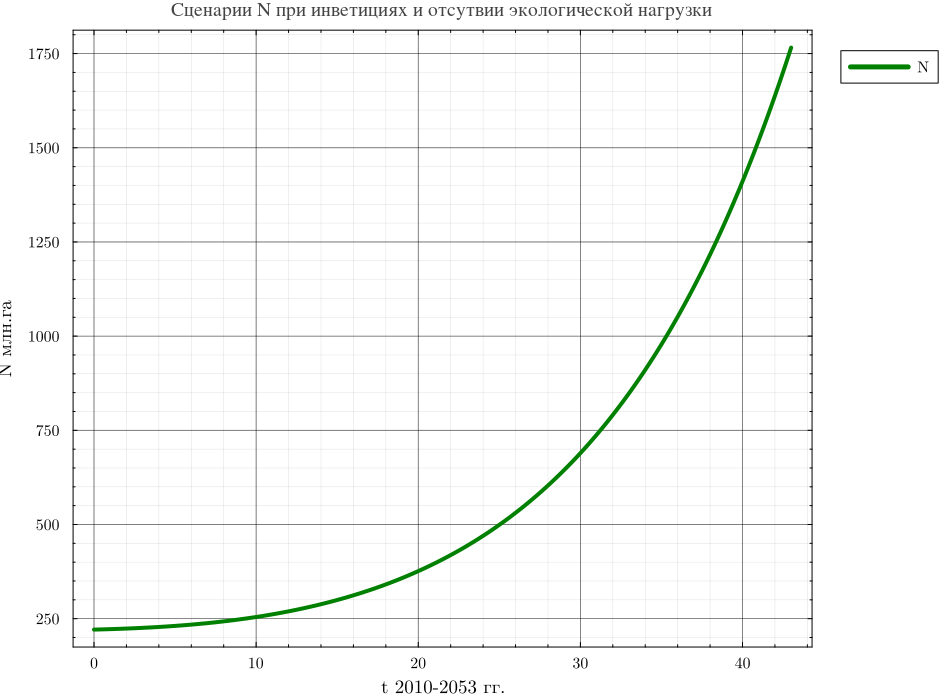
Где -функция, в которой интегрированы введенные выше соотношения. Решение этого уравнения графически представлено ниже. Как видно из рисунка, в отсутствие негативного воздействия на природный капитал, он при заданной стратегии роста инвестиций и их инновационности может вырасти за 40 лет почти в 20 раз.
Естественно в условиях значительной антропогенной нагрузки природ-ный капитал АСЭЭС так изменяться во времени не будет. Общая динамика изменения природного капитала для разных сценариев и «стратегий» при-роды может быть получена как результат решения следующих дифференци-альных уравнений:
Графически решения этих уравнений представлены ниже.
#Модель трансформации природного капитала АПК
#1. Позитивное воздейcтвие человека учитывается в модели
#2. Рассматривается первая "стратегия природы"- случай a)
#3. Рассматриваются все три функции относительной экологической нагрузки Dотн(t)
using DifferentialEquations, Plots, PlotThemes
using LaTeXStrings
#----решение дифференциального уравнения (25)
function f_V!(du, u, p, t)
γV =(γ_0*exp(0.246*t))/(γ_n+γ_0*(exp(0.246*t)-1))
InvV =(Inv_n*exp(0.12*t))/(Inv_n + Inv_0*(exp(0.12*t)-1))
giV =InvV*γV
bV =(b_n*exp(0.1*giV))/(b_n+b_0*(exp(0.1*giV)-1))
V =(1 - (1/bV))
du[1] = u[1] * V
end
#ВХОДНЫЕ ПАРАМЕТРЫ
at1=0.0
at2=0.0
at3=0.0
#1
tn =43.0 #Конец сценария
a_pr =0.5
m = 1.45
kdem = 0.90
N0 = 221.0
#2
b_0 =1.0
b_n = 1.15
γ_0 = 0.5
γ_n = 1.4
Inv_0 = 1.0
Inv_n = 10.0
tspan = (0.0, tn)
u0 = [N0]
p = (b_0,b_n,γ_0,γ_n,Inv_0,Inv_n)
probV = ODEProblem(f_V!, u0, tspan, p)
solV = solve(probV, abstol=1e-8, reltol=1e-8);
TV = deepcopy(solV.t)
FV = deepcopy(solV.u)
FV = reduce(vcat, FV);
theme(:dao)
default(titlefont=(12, "times"), legendfontsize=10, guidefont=(12, :black), tickfont=(10, :black))
plot(TV, FV, title="Сценарии N при инветициях и отсутвии экологической нагрузки", ylabel="N млн.га", xlabel="t", lw=2, linecolor=:green, wsize=(650, 500),label=L"N(t)", legend=:topleft)
plot!([0.0], [221.0], label=L"N_0=221 млн.га",
seriescolor=:green,
marker=:circle,
markersize=6,
markercolor=:green,
markerstrokecolor=:green)
#--------решение объединенного дифференциального уравнения (26a)
p = (a_pr, m, kdem,b_0,b_n,γ_0,γ_n,Inv_0,Inv_n)
#---АПОКАЛИПСИС---------------------------------------------------------
function f_NV1!(du, u, p, t)
D_otn11 = 0.229 * exp(0.06 * t)
w = 1 - (kdem / (1 - a_pr * D_otn11^m))
γV =(γ_0*exp(0.246*t))/(γ_n+γ_0*(exp(0.246*t)-1))
InvV =(Inv_n*exp(0.12*t))/(Inv_n + Inv_0*(exp(0.12*t)-1))
giV =InvV*γV
bV =(b_n*exp(0.1*giV))/(b_n+b_0*(exp(0.1*giV)-1))
V =(1 - (1/bV))
du[1] = u[1]*w + u[1]*V
end
tspan = (0.0, 25)
p = (a_pr,m,kdem,b_0,b_n,γ_0,γ_n,Inv_0,Inv_n)
probNV1 = ODEProblem(f_NV1!, u0, tspan, p)
solNV1 = solve(probNV1, abstol=1e-8, reltol=1e-8);
TNV1 = deepcopy(solNV1.t)
FNV1 = deepcopy(solNV1.u)
FNV1 = reduce(vcat, FNV1);
#--------------ПЛОХОЙ СЦЕНАРИЙ--------------------------------------------
function f_NV2!(du, u, p, t)
D_otn12 = 0.2289*exp(0.0344*t)
at2= -(a_pr*D_otn12^m)+1
w = (1 - (kdem/(at2)))
γV = (γ_0 * exp(0.246 * t)) / (γ_n + γ_0 * (exp(0.246 * t) - 1))
InvV = (Inv_n * exp(0.12 * t)) / (Inv_n + Inv_0 * (exp(0.12 * t) - 1))
giV = InvV * γV
bV = (b_n * exp(0.1 * giV)) / (b_n + b_0 * (exp(0.1 * giV) - 1))
V = (1 - (1 / bV))
du[1] = u[1] * w + u[1] * V
end
tspan = (0.0, tn)
probNV2 = ODEProblem(f_NV2!, u0, tspan, p)
solNV2 = solve(probNV2, abstol=1e-8, reltol=1e-8);
TNV2 = deepcopy(solNV2.t)
FNV2 = deepcopy(solNV2.u)
FNV2 = reduce(vcat, FNV2);
#--------------ХОРОШИЙ СЦЕНАРИЙ--------------------------------------------
function f_NV3!(du, u, p, t)
D_otn13 =(0.6329*exp(0.075*t))/(2.8+1.165*(-1+exp(0.075*t)))
at3=-(a_pr*D_otn13^m)+1
w = (1 - (kdem/(at3)))
γV = (γ_0 * exp(0.246 * t)) / (γ_n + γ_0 * (exp(0.246 * t) - 1))
InvV = (Inv_n * exp(0.12 * t)) / (Inv_n + Inv_0 * (exp(0.12 * t) - 1))
giV = InvV * γV
bV = (b_n * exp(0.1 * giV)) / (b_n + b_0 * (exp(0.1 * giV) - 1))
V = (1 - (1 / bV))
du[1] = u[1] * w + u[1] * V
end
probNV3 = ODEProblem(f_NV3!, u0, tspan, p)
solNV3 = solve(probNV3, abstol=1e-8, reltol=1e-8);
TNV3 = deepcopy(solNV3.t)
FNV3 = deepcopy(solNV3.u)
FNV3 = reduce(vcat, FNV3);
#----------------ПОСТРОЕНИЕ ГРАФИКОВ--------------
theme(:dao)
default(titlefont=(14, "times"), legendfontsize=8, guidefont=(12, :black), tickfont=(10, :black))
plot(TNV1, FNV1, title="Сценарии развития N при инвестициях\n первая стратегия природы", ylabel="N млн.га", xlabel="t", lw=2, linecolor=:red, label="Сценарий 1", wsize=(850, 700), legend=:topleft)
plot!(TNV2, FNV2, lw=2, linecolor=:blue, label="Сценарий 2")
plot!(TNV3, FNV3, lw=3, linecolor=:green, label="Сценарий 3")
hline!([N0 * 0.1], lw=2, lc=:red, linestyle=:dash, label="Граница зоны\n разрушения 10% от N0")
plot!([0.0], [221.0], label=L"N_0=221 млн.га",
seriescolor=:green,
marker=:circle,
markersize=6,
markercolor=:green,
markerstrokecolor=:green)
#Модель трансформации природного капитала АПК
#1. Позитивное воздейcтвие человека учитывается в модели
#2. Рассматривается вторая "стратегия природы"- случай б)
#3. Рассматриваются все три функции относительной экологической нагрузки Dотн(t)
using DifferentialEquations, Plots, PlotThemes
using LaTeXStrings
#ВХОДНЫЕ ПАРАМЕТРЫ
at1 = 0.0
at2 = 0.0
at3 = 0.0
#1
tn = 43.0 #Конец сценария
a_pr = 0.5
m = 1.45
kdem = 0.45
N0 = 221.0
#2
b_0 = 1.0
b_n = 1.14
γ_0 = 0.5
γ_n = 1.4
Inv_0 = 5.0
Inv_n = 150.0
u0 = [N0]
#--------решение объединенного дифференциального уравнения (26a)
#---АПОКАЛИПСИС---------------------------------------------------------
function f_NVb1!(du, u, p, t)
D_otn21 = 0.229*exp(0.06*t)
w = 1 - 1/(1-a_pr*kdem*D_otn21^m)
γV = (γ_0 * exp(0.246 * t)) / (γ_n + γ_0 * (exp(0.246 * t) - 1))
InvV = (Inv_n * exp(0.12 * t)) / (Inv_n + Inv_0 * (exp(0.12 * t) - 1))
giV = InvV * γV
bV = (b_n * exp(0.1 * giV)) / (b_n + b_0 * (exp(0.1 * giV) - 1))
V = (1 - (1 / bV))
du[1] = u[1] * w + u[1] * V
end
tspan = (0.0, 30)
p = (a_pr, m, kdem, b_0, b_n, γ_0, γ_n, Inv_0, Inv_n)
probNVb1 = ODEProblem(f_NVb1!, u0, tspan, p)
solNVb1 = solve(probNVb1, abstol=1e-8, reltol=1e-8);
TNVb1 = deepcopy(solNVb1.t)
FNVb1 = deepcopy(solNVb1.u)
FNVb1 = reduce(vcat, FNVb1);
#--------------СЦЕНАРИЙ 2 ПЛОХОЙ------------------------------------------
function f_NVb2!(du, u, p, t)
D_otn22 = 0.2289*exp(0.0344*t)
w = 1 - 1/(1-a_pr*kdem*D_otn22^m)
γV = (γ_0 * exp(0.246 * t)) / (γ_n + γ_0 * (exp(0.246 * t) - 1))
InvV = (Inv_n * exp(0.12 * t)) / (Inv_n + Inv_0 * (exp(0.12 * t) - 1))
giV = InvV * γV
bV = (b_n * exp(0.1 * giV)) / (b_n + b_0 * (exp(0.1 * giV) - 1))
V = (1 - (1 / bV))
du[1] = u[1] * w + u[1] * V
end
tspan = (0.0, tn)
probNVb2 = ODEProblem(f_NVb2!, u0, tspan, p)
solNVb2 = solve(probNVb2, abstol=1e-8, reltol=1e-8);
TNVb2 = deepcopy(solNVb2.t)
FNVb2 = deepcopy(solNVb2.u)
FNVb2 = reduce(vcat, FNVb2);
#--------------СЦЕНАРИЙ 3--ХОРОШИЙ СЦЕНАРИЙ-----------------------------------
function f_NVb3!(du, u, p, t)
D_otn13 = (0.6329*exp(0.075*t))/(2.8+1.165*(-1+exp(0.075*t)))
w = 1 - 1/(1-a_pr*kdem*D_otn13^m)
γV = (γ_0 * exp(0.246 * t)) / (γ_n + γ_0 * (exp(0.246 * t) - 1))
InvV = (Inv_n * exp(0.12 * t)) / (Inv_n + Inv_0 * (exp(0.12 * t) - 1))
giV = InvV * γV
bV = (b_n * exp(0.1 * giV)) / (b_n + b_0 * (exp(0.1 * giV) - 1))
V = (1 - (1 / bV))
du[1] = u[1] * w + u[1] * V
end
tspan = (0.0, tn)
probNVb3 = ODEProblem(f_NVb3!, u0, tspan, p)
solNVb3 = solve(probNVb3, abstol=1e-8, reltol=1e-8);
TNVb3 = deepcopy(solNVb3.t)
FNVb3 = deepcopy(solNVb3.u)
FNVb3 = reduce(vcat, FNVb3);
#----------------ПОСТРОЕНИЕ ГРАФИКОВ--------------
theme(:dao)
default(titlefont=(14, "times"), legendfontsize=8, guidefont=(12, :black), tickfont=(10, :black))
plot(TNVb1, FNVb1, title="Сценарии развития N при инвестициях\n вторая стратегия природы", ylabel="N млн.га", xlabel="t", lw=2, linecolor=:red, label="Сценарий 1", wsize=(950, 700), legend=:outertopright)
plot!(TNVb2, FNVb2, lw=2, linecolor=:blue, label="Сценарий 2")
plot!(TNVb3, FNVb3, lw=3, linecolor=:green, label="Сценарий 3")
hline!([N0 * 0.1], lw=2, lc=:red, linestyle=:dash, label="Граница зоны\n разрушения 10% от N0")
plot!([0.0], [221.0], label=L"N_0=221 млн.га",
seriescolor=:green,
marker=:circle,
markersize=6,
markercolor=:green,
markerstrokecolor=:green)
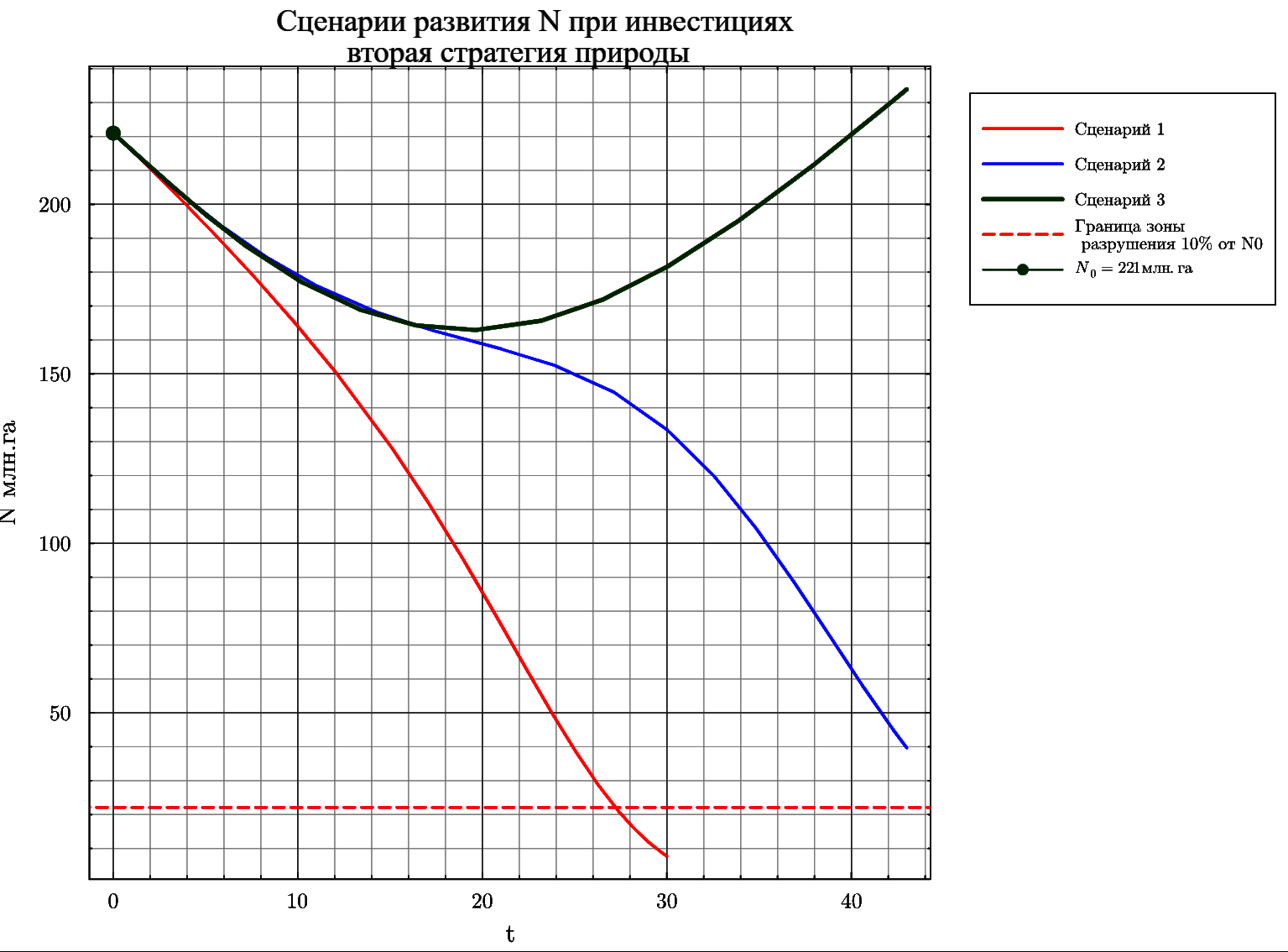
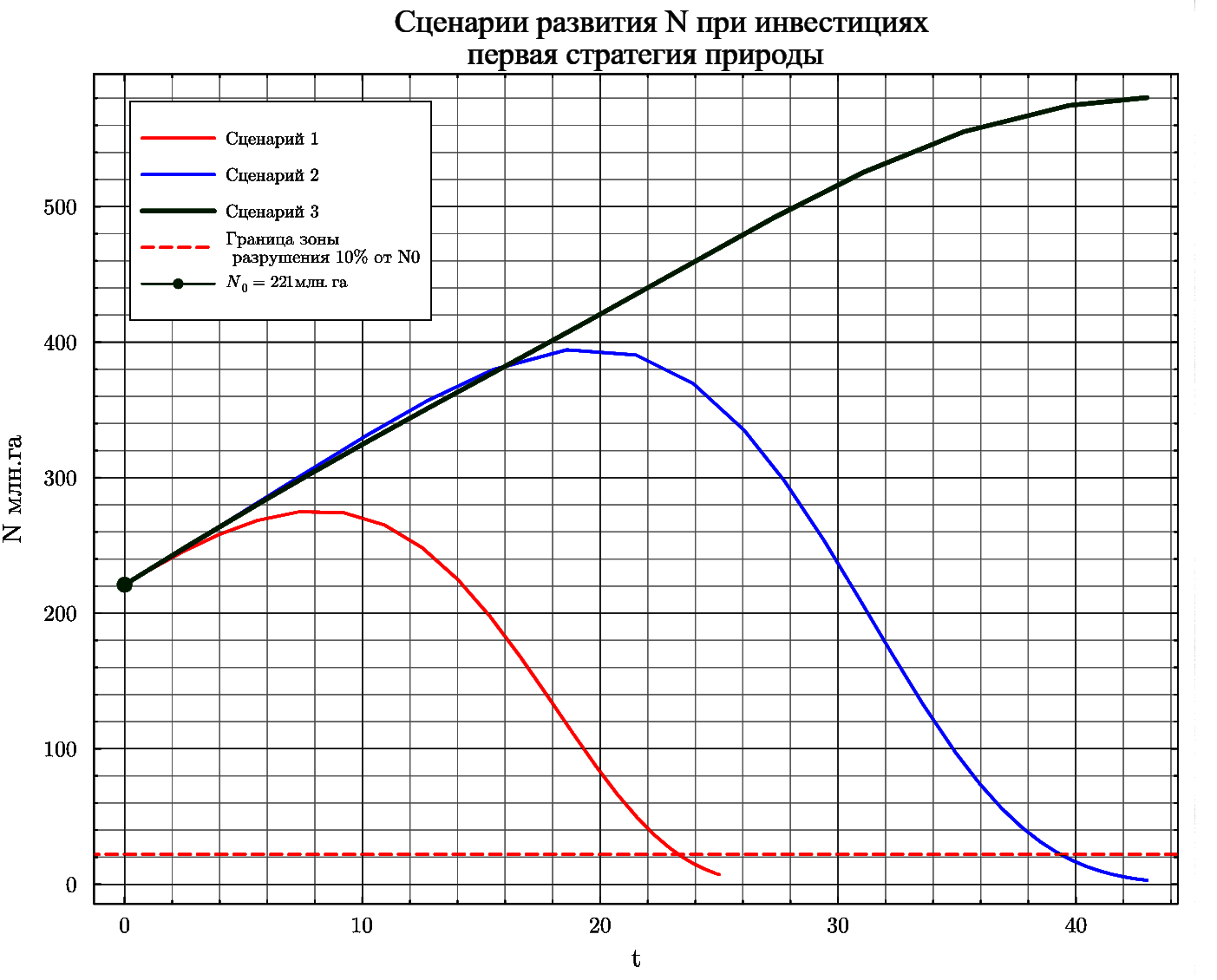
Графики наглядно демонстрируют, что негативные сценарии (1,2) по экологической нагрузке не могут быть компенсированы только за счет инвестиций в повышение продуктивности земли при любой стратегии природы, то есть разрушение практически неизбежно.А при экологичном сценарии (3) в зависимости от стратегии природы может быть обеспечен и значительный рост за 43 года с дальнейшей стабилизацией(вариант а) или снижение до 40-50 процентов с дальнешем ростом до первоначального уровня с небольшим ростом и стабилизацией (вариант б)
Полученные результаты по формализации описания динамики основного, человеческого и природного капитала показывают достаточно большие возможности предлагаемого подхода для сценарного анализа развития экономического потенциала АСЭЭС на больших временных горизонтах. Необходимо обобщение полученных результатов в виде достаточно строгой теории трансформации факторов развития АСЭЭС.
Решим дифференциальные уравнения (17), (25) , (26) при следующих начальных условиях N(0) = 221 (это площадь земель сельскохозяйственного назначения на 2011 год в млн. га) на основе разработки и использования Engee-моделей.
Реализующая решение уравнений (17) при начальных условиях N(0) = 221 на интервале t=[0.0, 43.0] при первой стратегии природы Engee-модель «W1.mdl» имеет следующий вид:
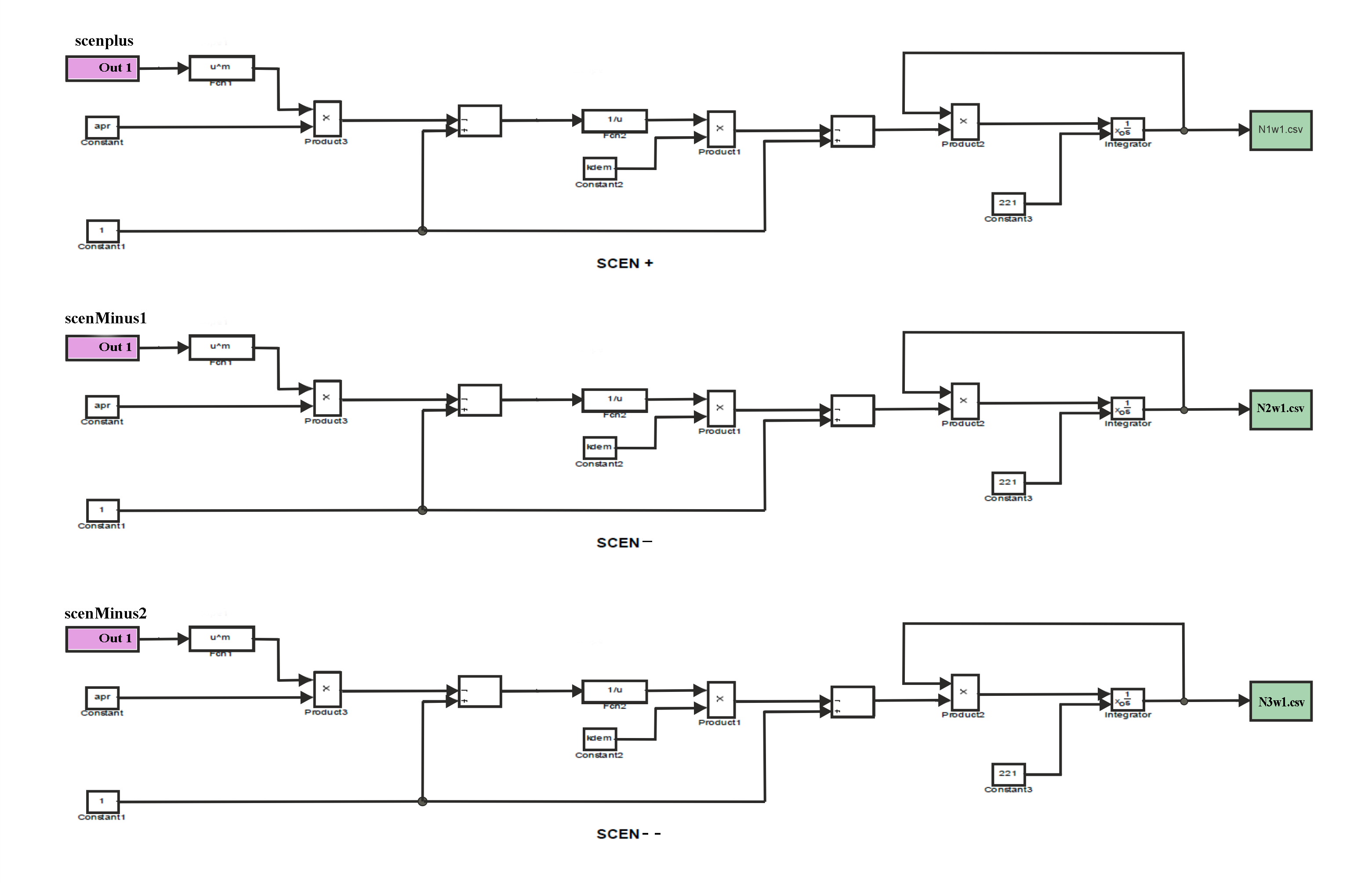
В этой Engee-модели используются три подмодели «scenplus»,«scenMINUS1» и «scenMINUS2». Подмодель «scenplus» описывает динами-
ку экологической нагрузки при оптимистическом сценарии. Она имеет следующий вид:
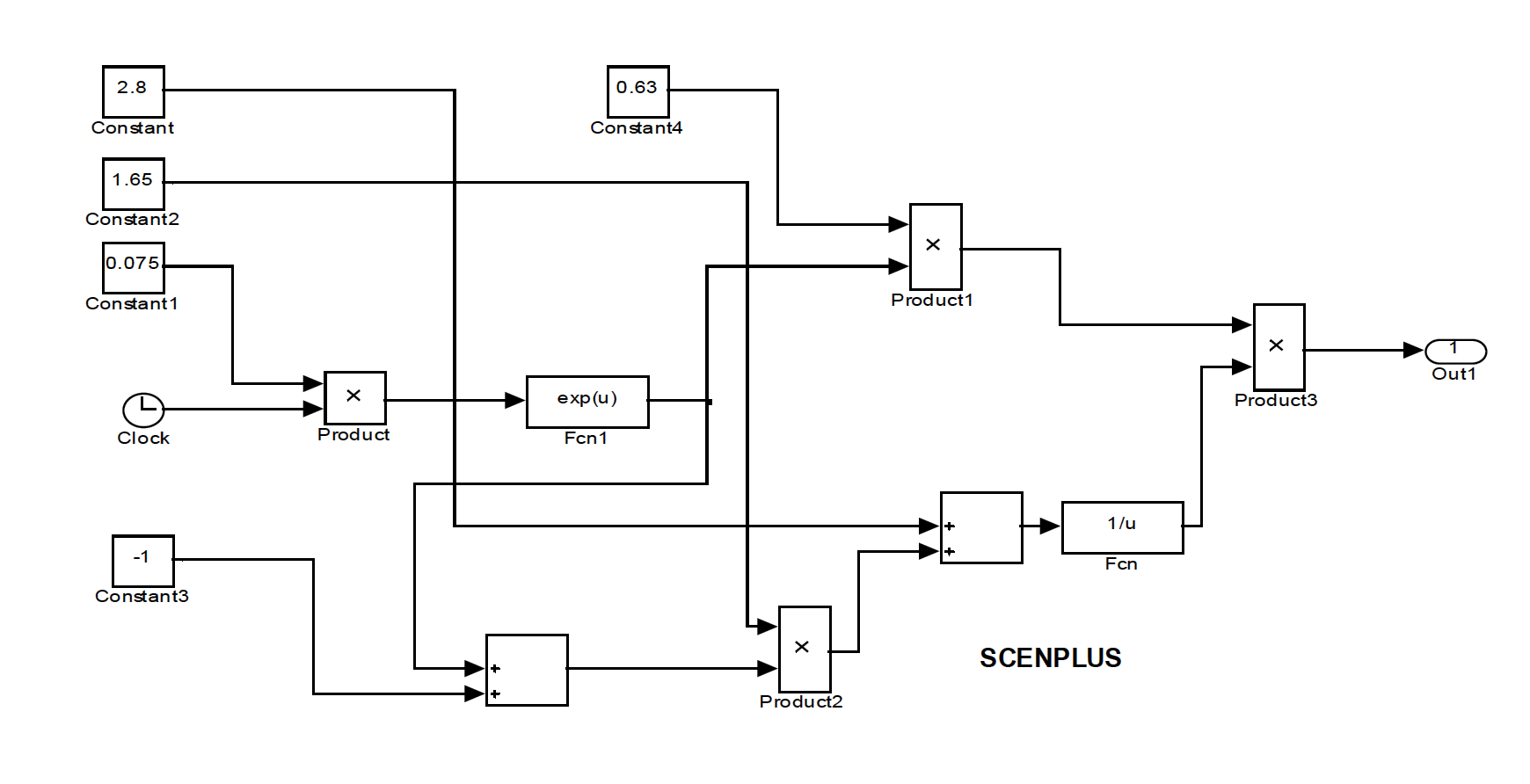
Подмодель «scenMINUS1» описывает динамику экологической нагрузки при пессимистическом сценарии.с=0.0344 Она имеет следующий вид:
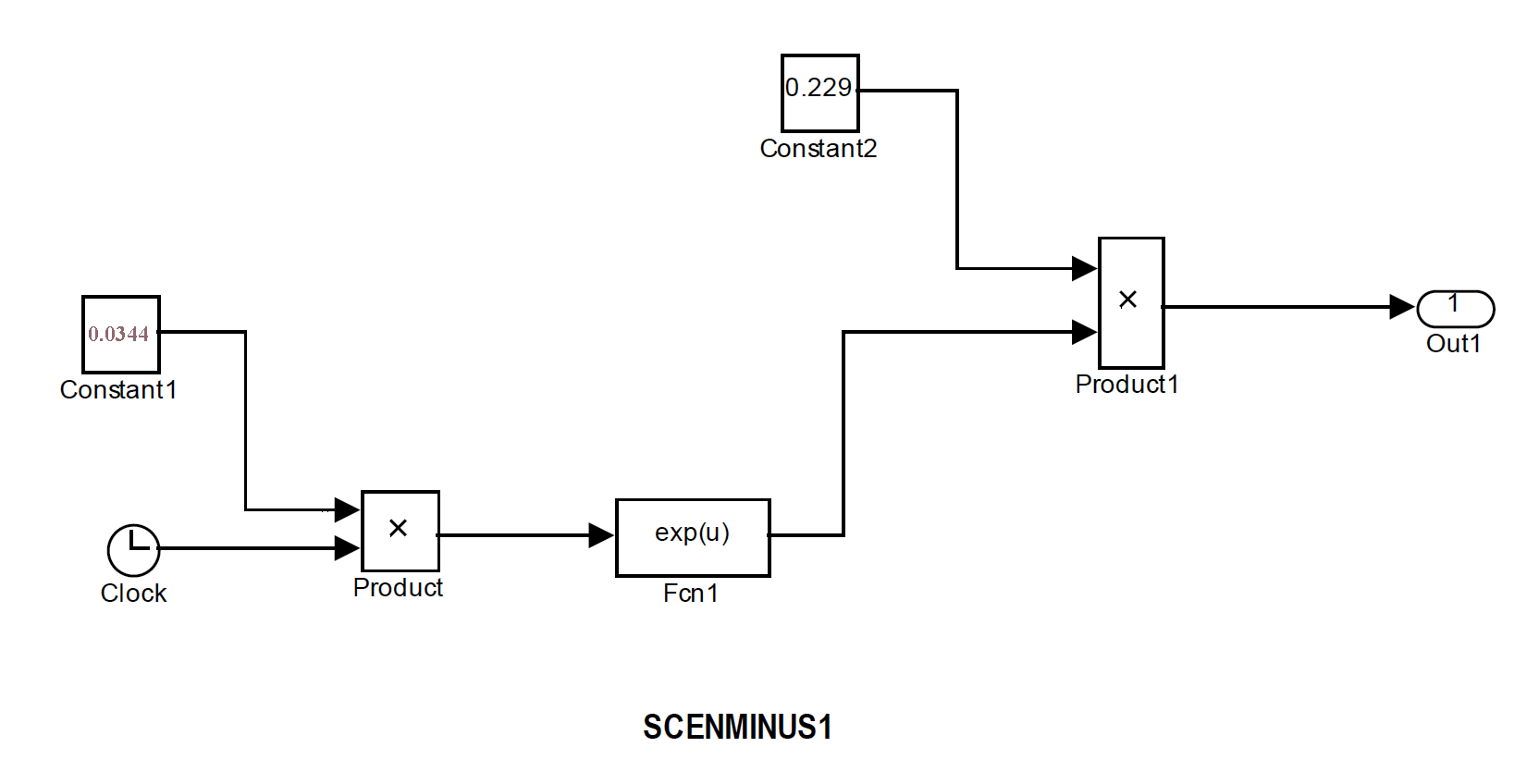
Подмодель «scenMINUS2» описывает динамику экологической нагрузки при предельно пессимистическом сценарии. Она имеет следующий вид:
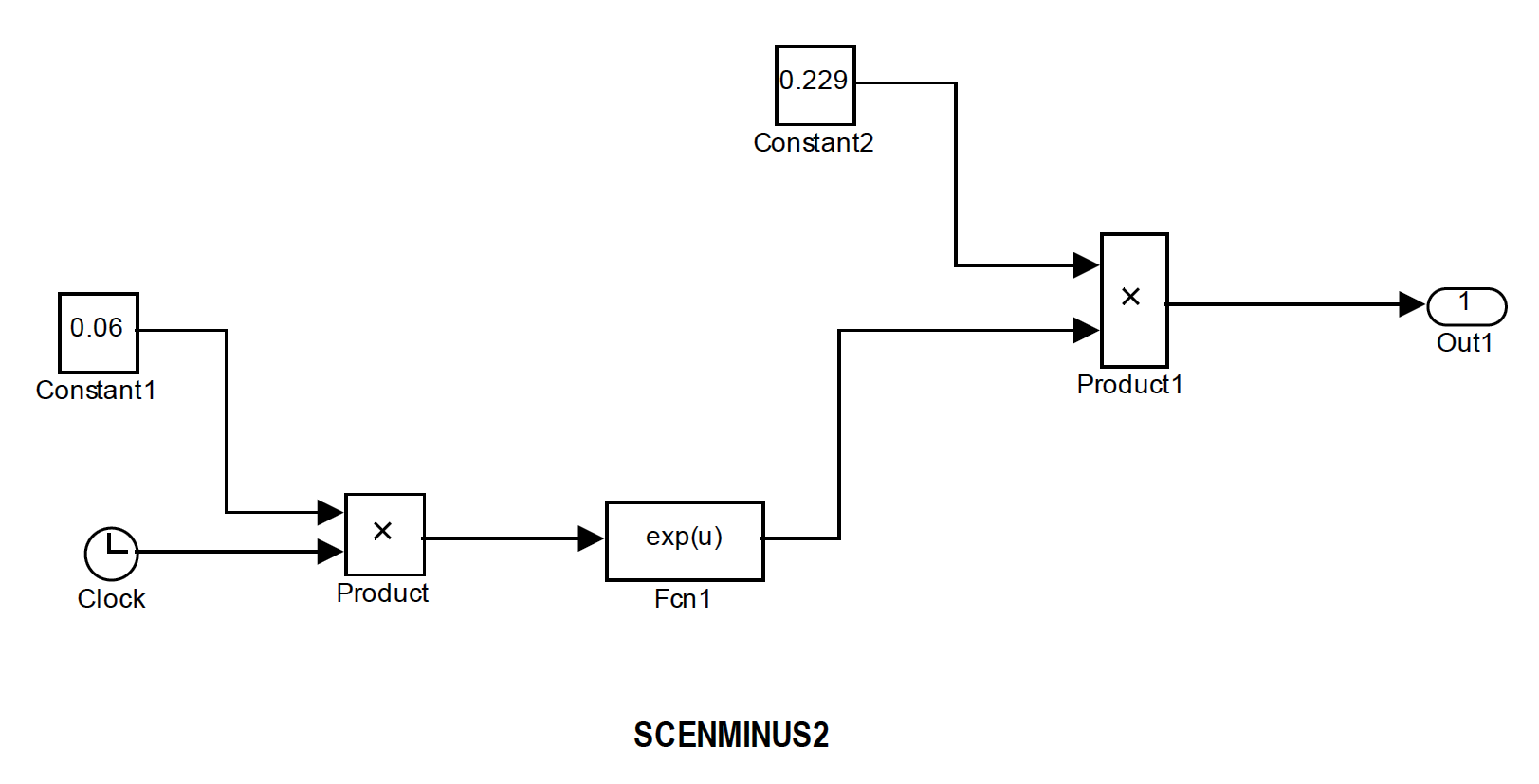
Для исследования с помощью этой модели динамики природного капитала агросистемы России был разработан скрипт:
#=Модель трансформации природного капитала АПК
1. Позитивное воздейcтвие человека отсутствует
2. Рассматривается первая "стратегия природы"- случай а)
3. Рассматриваются все три функции относительной экологической нагрузки Dотн(t)=#
using RDatasets, Plots, PlotThemes
using CSV, DataFrames, LaTeXStrings
#открытие модели
modelName = "W1";
PID_model = modelName in [m.name for m in engee.get_all_models()] ? engee.open(modelName) :
engee.load("/user/ModTN/$(modelName).engee");
engee.set_param!(modelName, "StopTime" => 43.0) # задание интервала моделирования
#параметры модели
#Предельный темп падения продуктивности земли
global apr=0.5;
#Параметр регулирующий скорость падения продуктивности земли
global m=1.45;
#Коэффициент демпфирования (самовосстановления) природного капитала
global kdem=0.94
engee.run(modelName) #запуск модели
N1w1t = CSV.read("N1w1.csv", DataFrame)
N2w1t = CSV.read("N2w1.csv", DataFrame)
N3w1t = CSV.read("N3w1.csv", DataFrame);
gr()
#plotly()
theme(:dao)
N0=221.0
default(titlefont=(12, "times"), legendfontsize=10, guidefont=(12, :black), tickfont=(10, :black))
plot(N1w1t[!, "time"], N1w1t[!, "N1w1t"], title="Сценарии развития N в отсутствии инвестиций\n (первая стратегия природы-случай а)", ylabel="N млн.га", xlabel="t 2010-2053 гг.", lw=2, linecolor=:green, label="Сценарий 1 + ",
wsize=(800, 500), legend=:outertopright)
plot!(N2w1t[!, "time"], N2w1t[!, "N2w1t"], lw=2, linecolor=:5, label="Сценарий 2 -")
plot!(N3w1t[1:3000, "time"], N3w1t[1:3000, "N3w1t"], lw=3, linecolor=:red, label="Сценарий 3 --")
hline!([N0 * 0.1], lw=2, lc=:red, linestyle=:dash, label="Граница зоны\n разрушения N")
Аналогично можно решить дифференциальные уравнения (17) с помощью Engee-моделей для второй стратегии природы (случай б)
Перейдем к решению в Engee уравнения (25). Реализующая решение уравнения (25) при начальных условиях N(0) = 221 на интервале t=[0.43] Engee-модель «V.mdl» имеет следующий вид:
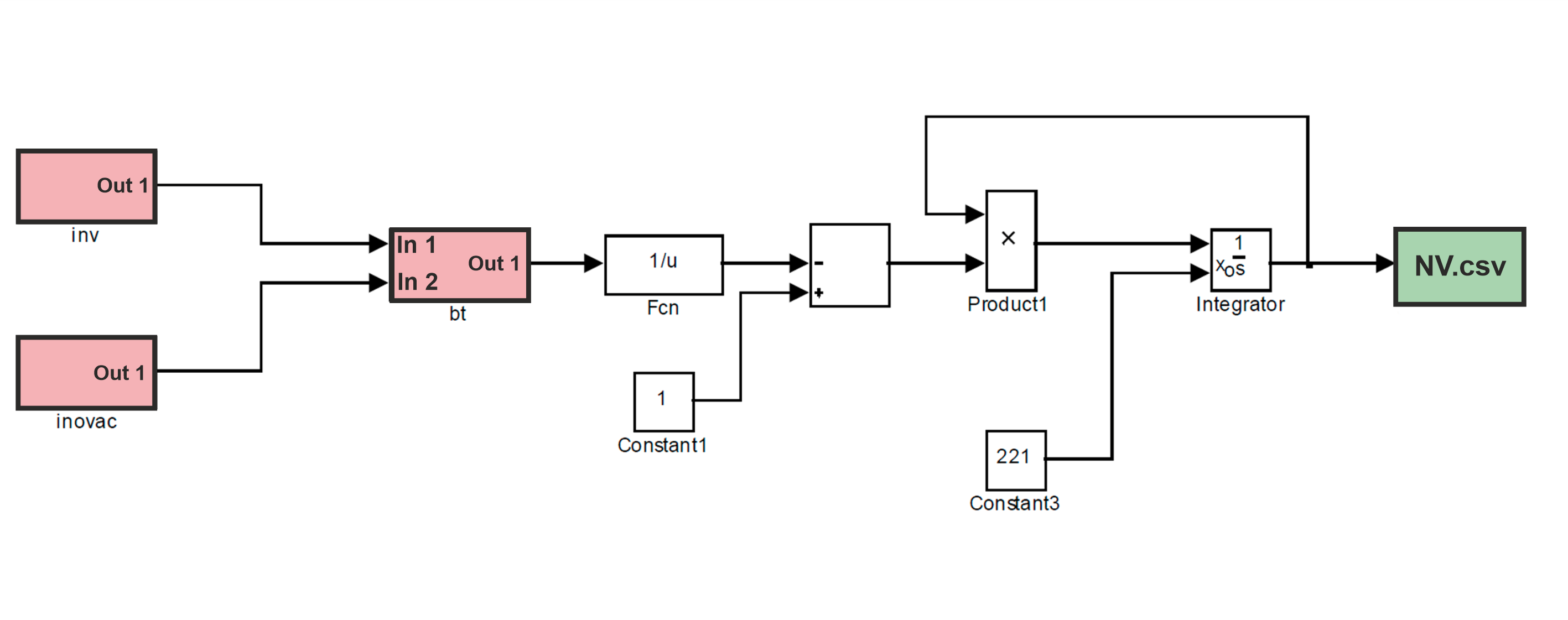
В этой Engee-модели используются три подмодели «inv», «inovac» и «bt». Подмодель «inv» описывает инвестиционную стратегию в природо-восстановительной деятельности и имеет следующий вид:
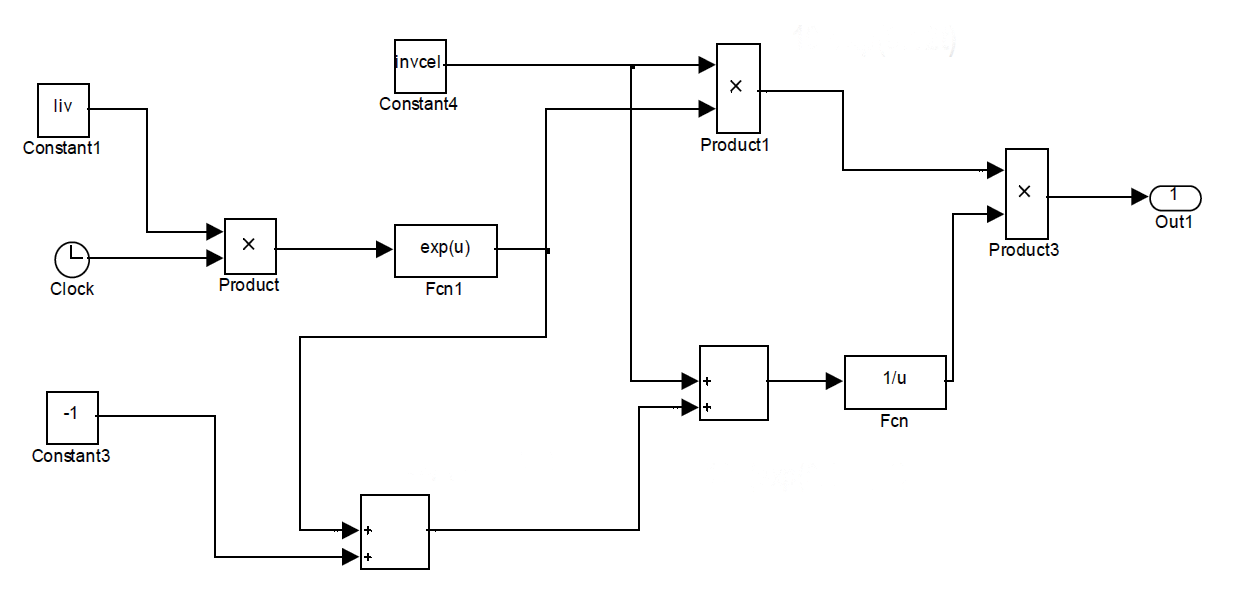
Подмодель «inovac» описывает инновационную стратегию в природо-восстановительной деятельности и имеет следующий вид:
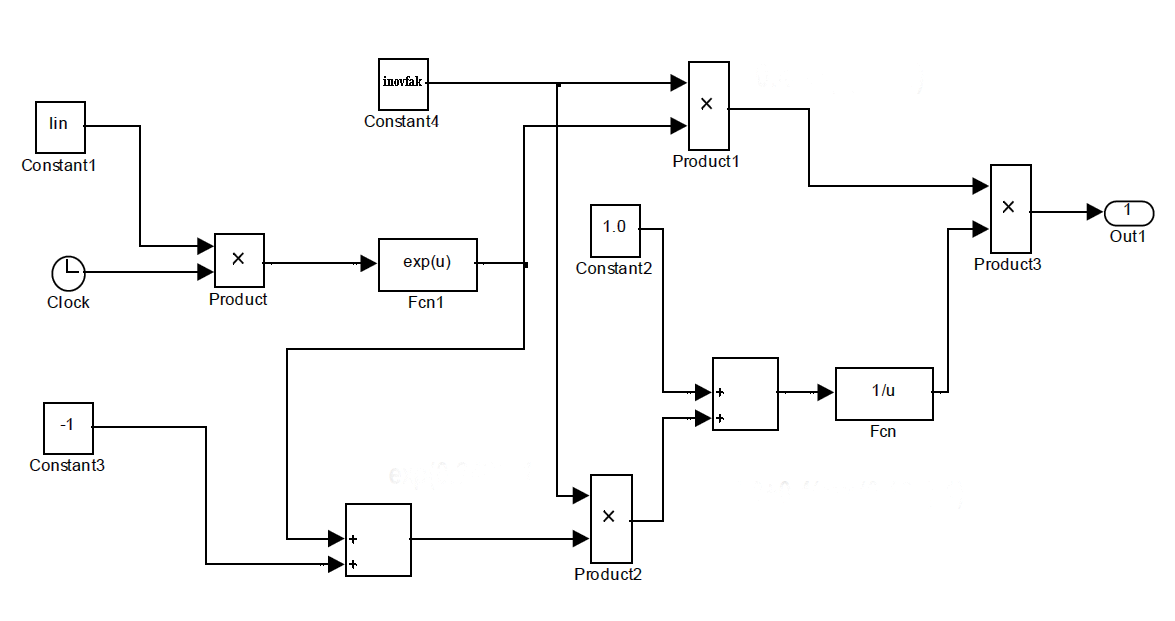
Подмодель «bt» описывает величину , определяющую продуктивность земли в любой момент времени, в зависимости от величины инвестиций на 1 га земли и уровня их инновационности. Она имеет следующий вид:
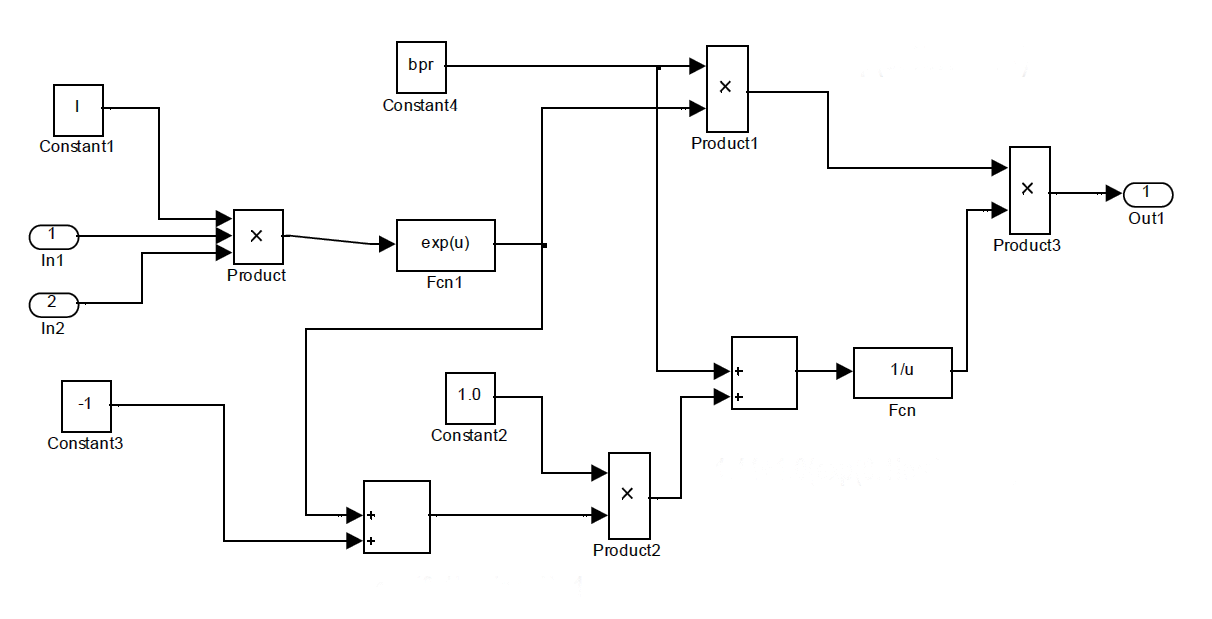
Для исследования с помощью этой модели динамики природного капитала агросистемы России был разработан соответствующий скрипт и получено следующее решение:
#Модель трансформации природного капитала АПК
#ИССЛЕДОВАНИЕ ДИНАМИКИ ПРИРОДНОГО КАПИТАЛА ПРИ ОСУЩЕСТВЛЕНИИ ПРИРОДОВОССТАНОВИТЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ
using RDatasets, Plots, PlotThemes
using CSV, DataFrames, LaTeXStrings
#открытие модели
modelName = "V";
PID_model = modelName in [m.name for m in engee.get_all_models()] ? engee.open(modelName) :
engee.load("/user/ModTN/$(modelName).engee");
engee.set_param!(modelName, "StopTime" => 43.0) # задание интервала моделирования
#параметры модели:
#Параметры определяюшие коэффициент роста продуктивности земли
bpr=1.14;
l=0.1;
#Параметры регулирующие динамику инновационности инвестиций
inovfak=0.4;
lin=0.24;
#Параметры регулирующие динамику инвестиций
liv=0.12;
invcel=10;
engee.run(modelName) #запуск модели
NVt = CSV.read("NV.csv", DataFrame);
gr()
#plotly()
theme(:dao)
default(titlefont=(12, "times"), legendfontsize=10, guidefont=(12, :black), tickfont=(10, :black))
plot(NVt[!, "time"], NVt[!, "NVt"], title="Сценарии N при инветициях и отсутвии экологической нагрузки",
ylabel="N млн.га", xlabel="t 2010-2053 гг.", lw=4, linecolor=:green, label="N",wsize=(950, 700), legend=:outertopright)
Реализующая решение уравнений (26) при начальных условиях N(0) = 221 на интервале t=[0.43] при первой стратегии природы Engee-модель «VW1» имеет следующий вид:
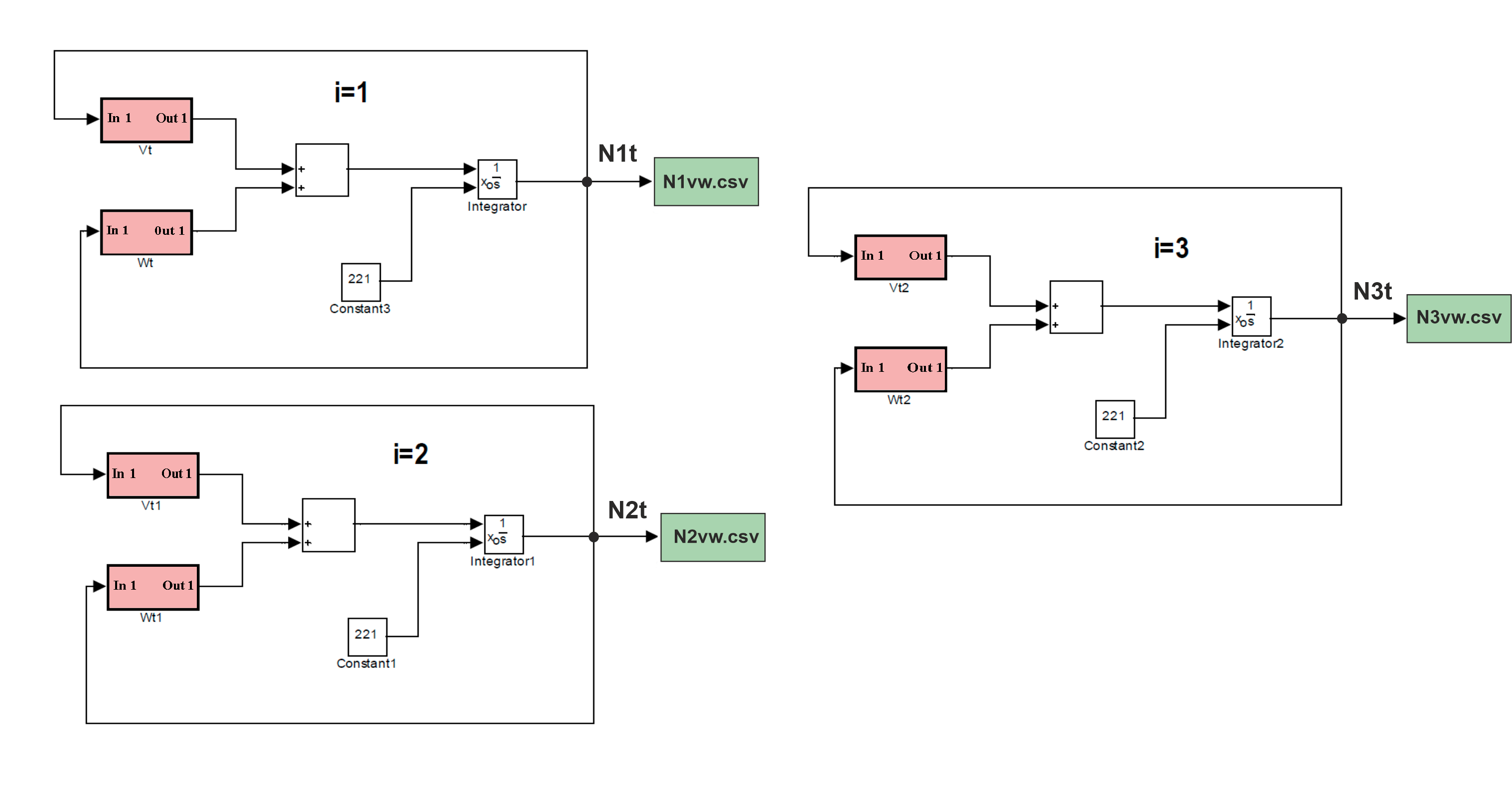
Эта Engee-модель имеет 3 уровня. На исходном 0-ом уровне реализованы три подсистемы, каждая из которых относится к соответствующему дифференциальному уравнению. Здесь в каждой подсистеме используются две подмодели «Vti», «Wti» i=0,1,2.
На 1-ом уровне реализованы подмодели «Vti» и подмодели «Wti» :
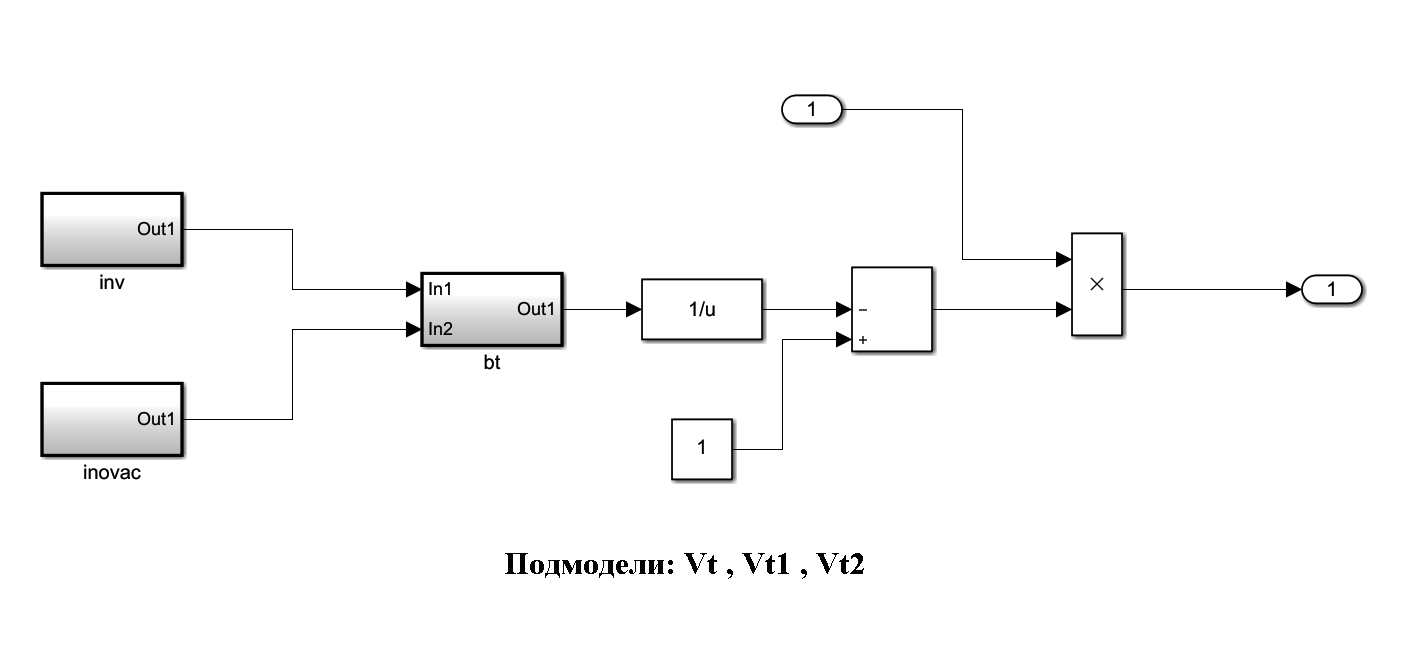
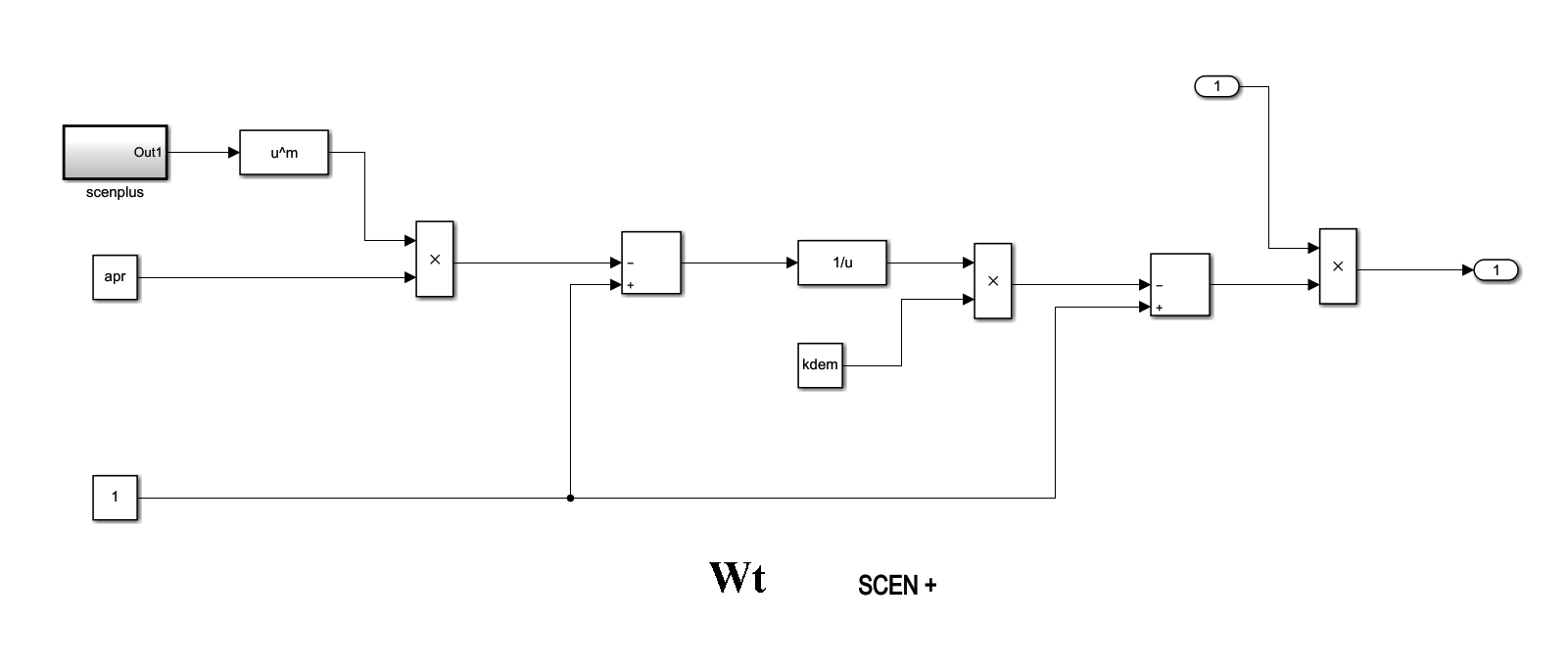
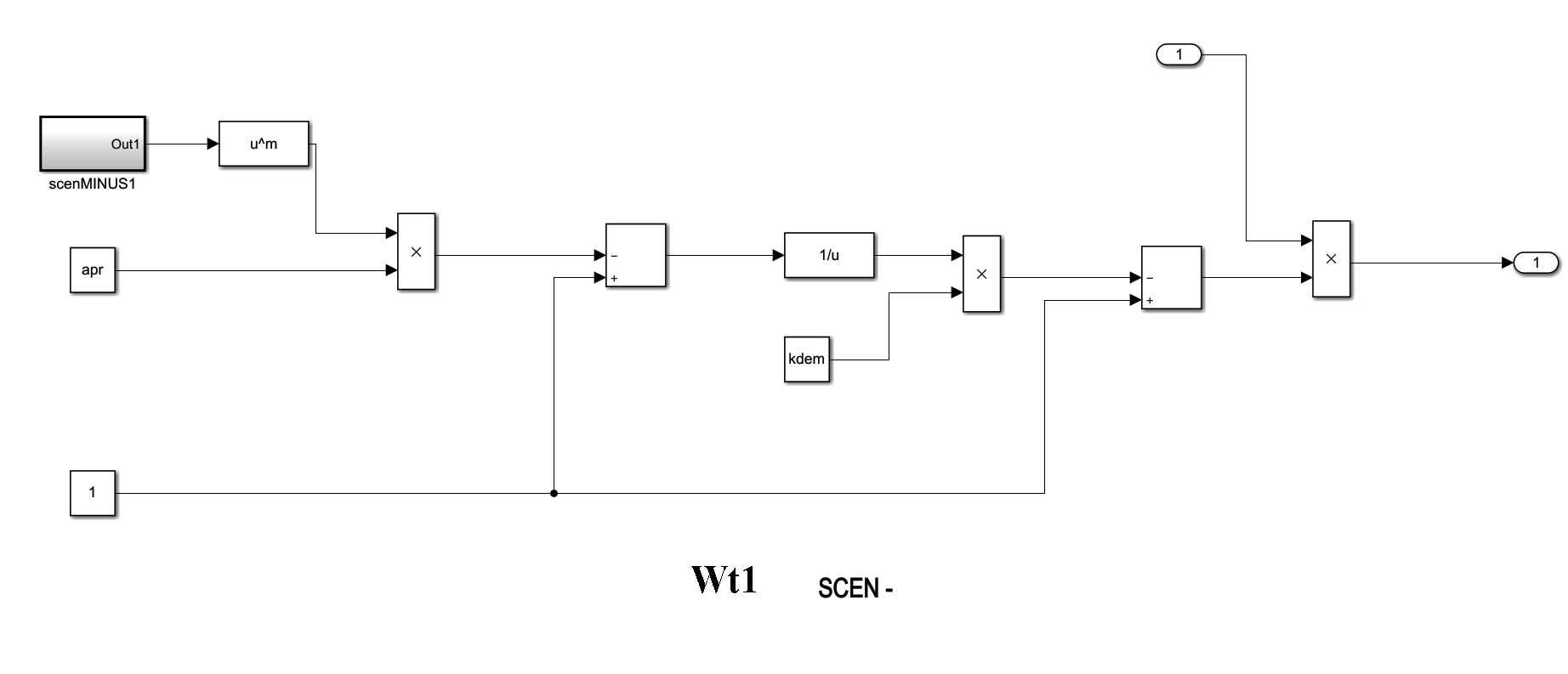
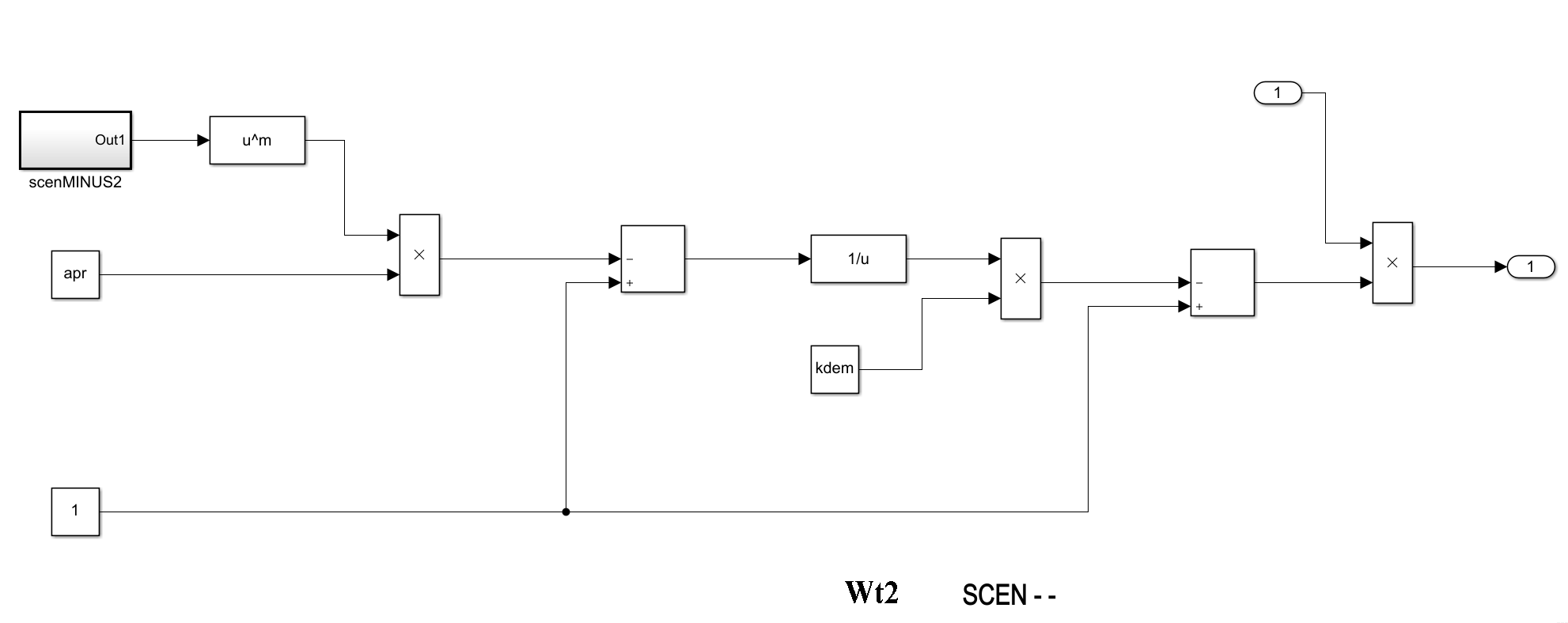
На третьем уровне реализованы подмодели «inv» «inovac» и «bt» для каждой «Vti» и подмодели соответствующих сценариев экологиче-
ской нагрузки для каждой «Wti». Схемы подмоделей: «inv», «inovac», «bt», «scenplus», «scenMinus1», «scenMinus2» были уже приведены нами выше.
Для исследования с помощью этой модели динамики природного капитала агросистемы России был разработан соответствующий скрипт и
получено следующее решение:
#Модель трансформации природного капитала АПК
#1. Позитивное воздейcтвие человека учитывается в модели
#2. Рассматривается первая "стратегия природы"- случай а)
#3. Рассматриваются все три функции относительной экологической нагрузки Dотн(t)
using RDatasets, Plots, PlotThemes
using CSV, DataFrames, LaTeXStrings
#открытие модели
modelName = "VW1";
PID_model = modelName in [m.name for m in engee.get_all_models()] ? engee.open(modelName) :
engee.load("/user/ModTN/$(modelName).engee");
engee.set_param!(modelName, "StopTime" => 43.0) # задание интервала моделирования
#Предельный темп падения продуктивности земли
apr=0.5;
#Параметр регулирующий скорость падения продуктивности земли
m=1.45;
#Коэффициент демпфирования (самовосстановления) природного капитала
kdem=0.94
#Параметры определяюшие коэффициент роста продуктивности земли
bpr=1.15;
l=0.1;
#Параметры регулирующие динамику инновационности инвестиций
inovfak=0.4;
lin=0.246;
#Параметры регулирующие динамику инвестиций
liv=0.12;
invcel=10.0;
engee.run(modelName) #запуск модели
N1t = CSV.read("N1vw.csv", DataFrame)
N2t = CSV.read("N2vw.csv", DataFrame)
N3t = CSV.read("N3vw.csv", DataFrame);
N0=221.0
gr()
#plotly()
theme(:dao)
default(titlefont=(12, "times"), legendfontsize=10, guidefont=(12, :black), tickfont=(10, :black))
plot(N1t[!, "time"], N1t[!, "N1t"], title="Сценарии развития N при инвестициях\n (первая стратегия природы-случай а)", ylabel="N млн.га", xlabel="t 2010-2053 гг.", lw=3, linecolor=:green, label="Сценарий 1 + ",
wsize=(1000, 800), legend=:outertopright)
plot!(N2t[!, "time"], N2t[!, "N2t"], lw=3, linecolor=:5, label="Сценарий 2 -")
plot!(N3t[1:3000, "time"], N3t[1:3000, "N3t"], lw=3, linecolor=:red, label="Сценарий 3 - -")
hline!([N0 * 0.1], lw=2, lc=:red, linestyle=:dash, label="Граница зоны\n разрушения 10% от N0")
plot!([0.0], [221.0], label=L"N_0=221 млн.га",
seriescolor=:green,
marker=:circle,
markersize=6,
markercolor=:green,
markerstrokecolor=:green)
Список используемых источников
-
Варюхин А. М., Гришин П.Н. Элементы экономической трансформатики.
На пути к теории устойчивого развития агросистем: методологические осно-
вания и базовые модели.– Саратов : Изд-во Сарат. ун-та, 2012. -
Лялин B.C. Статистика: теория и практика в Excel: учеб. пособие /B.C. Ля-
лин, И.Г. Зверева, Н.Г. Никифорова. — М.: Финансы и статистика; ИНФРА-
М, 2010. -
Варюхин А.М., Швейкин В.А. Аграрный ресурсно-производственный по-
тенциал как экономическая категория (сущность, содержание, диалектика
движения) // Материалы научных чтений, посвященных В.Б. Островскому).
"Островские чтения 2005" 23 ноября 2005 г. / РАН. Институт аграрных про-
блем. - Саратов, 2005. -
Варюхин А.М., Кравченко В.В., Наташкин В.В. Системный анализ ресурс-
ного потенциала региональной агросистемы и методические подходы к его
комплексной оценке.- Саратов: Изд-во Сарат. гос. социально-эконом. уни-
верситета, 2000. -
Гилфасон Т. Ресурсы, сельское хозяйство и экономический рост в странах
с переходной экономикой. // ЭКОВЕСТ (2002) -
Варюхин А.М., Гришин П.Н., Кравченко В.В. Теоретико-
методологические основы системного исследования плодородия почвы в
экосистемах и агроэкосистемах. – Саратов: Издат. Центр СГЭА, 1998. -
Варюхин А.М., Гришин П.Н., Кравченко В.В Прикладная методология и
методика математического моделирования почвенных и гроценотических
процессов. // Моделирование параметров почвенного плодородия:
тематический сборник. -Саратов: Издат. Центр СГЭА, 1998. -
Варюхин А.М., Гришин П.Н. Роль информационной инфраструктуры в
становлении и развитии рыночных отношений, создании условий стабилиза-
ции и перехода к этапу экономического роста агропромышленного производ-
ства (макроэкономический анализ). // Сб. научных работ специалистов и эко-
номистов “Экономические проблемы региона ’’ № 2., Министерство эконо-
мики и инвестиционной политики Саратовской области, 1997. -
Варюхин А.М., Гришин П.Н. Оценка уровня развития информационной
инфраструктуры региональных агросистем. // Сб. научных работ специали-
стов и экономистов “Экономические проблемы региона ’’ № 3-№4., Мини-
стерство экономики и инвестиционной политики Саратовской области., 1997. -
Бобылев С.Н. Воздействие изменения климата на сельское хозяйство и
водные ресурсы России. ФОНД «Защита природы». М., 2003. -
Государственные доклады о состоянии природной среды Российской Фе-
дерации. М., 1995-2000. -
Варюхин А.М., Гришин П.Н. Использование эконометрических моделей
для оценки совокупного ресурсного потенциала сельскохозяйственного про-
изводства. Сб. научных работ специалистов и экономистов “Экономические
проблемы региона ’’ № 3-№4., Министерство экономики и инвестиционной
политики Саратовской области., 1997. -
Урманцев Ю.А. Эволюционика или общая теория развития систем приро-
ды, общества и мышления. - М., 2009. -
Данилов Н.Н. Курс математической экономики.- М.: Высш. шк., 2006.
-
Просолов А.В. Математические методы экономической динамики. –
СПб.: Издательство «Лань», 2008. -
Колесов Ю.Б., Сениченков Ю.Б. Моделирование систем. Динамические и
гибридные системы. -Санкт Петербург: БХВ- Петербург 2006.