Моделирование движения частиц, визуализация гравитации

Гравитация — одна из фундаментальных сил природы, определяющая движение небесных тел и объектов на их поверхности. Однако сила тяжести существенно различается на разных планетах Солнечной системы: от 3.7 м/с² на Меркурии до 24.79 м/с² на Юпитере. Эти различия не просто цифры в учебнике — они кардинально меняют физику движения объектов.

В этой статье мы разберем интерактивный пример, который наглядно демонстрирует, как одни и те же частицы ведут себя под действием гравитации разных планет. Пример не только показывает физические принципы, но и демонстрирует различные возможности языка от расчётов и визуализации, до оптимизации вычислений.

Давайте поэтапно разберем код, начиная с базовых физических констант и заканчивая созданием интерактивной визуализации. Это поможет понять не только физику гравитации, но и практические аспекты программирования научных симуляций.

using Random

Первое что мы рассмотрим это PLANET_GRAVITY, словарь-константа, содержащий значения ускорения свободного падения (g) для различных небесных тел.

PLANET_GRAVITY = Dict(
    "Меркурий" => 3.7,
    "Венера" => 8.87,
    "Земля" => 9.81,
    "Марс" => 3.711,
    "Юпитер" => 24.79,
    "Сатурн" => 10.44,
    "Уран" => 8.69,
    "Нептун" => 11.15,
    "Луна" => 1.62
)

Dict{String, Float64} with 9 entries:
  "Земля"    => 9.81
  "Марс"     => 3.711
  "Уран"     => 8.69
  "Юпитер"   => 24.79
  "Меркурий" => 3.7
  "Сатурн"   => 10.44
  "Нептун"   => 11.15
  "Венера"   => 8.87
  "Луна"     => 1.62

Далее Particle — это изменяемая структура (mutable struct), описывающая отдельную частицу в симуляции.

Поля структуры:

x::Float32, y::Float32 — координаты частицы в двумерном пространстве
- Используется Float32 для экономии памяти при обработке множества частиц
vx::Float32, vy::Float32 — компоненты скорости частицы по осям X и Y
- Определяют направление и скорость движения
color::Symbol — цвет частицы для визуализации
- Например: :red, :blue, :green

mutable struct Particle
    x::Float32
    y::Float32
    vx::Float32
    vy::Float32
    color::Symbol
end

Первая функция в коде - это generate_same_particles(), она создаёт 6 одинаковых частиц с фиксированными начальными условиями:

Random.seed!(42) устанавливает зерно генератора случайных чисел, обеспечивая идентичную генерацию при каждом запуске
Диапазоны координат и скоростей:
- X: -3 до 3 (rand() * 6 - 3)
- Y: 2 до 4 (rand() * 2 + 2) — частицы создаются в верхней части
- Vx: -1 до 1 (rand() * 2 - 1) — случайная горизонтальная скорость
- Vy: 0 — нулевая начальная вертикальная скорость
Цвета назначаются по порядку из фиксированного списка [:red, :blue, :green, :orange, :purple, :cyan]

Функция возвращает массив из 6 частиц Particle[], которые будут использоваться для сравнения гравитации на разных планетах при одинаковых начальных условиях.

В реализации есть одна интересная особенность, числа с суффиксом f0 (6f0, 3f0, 2f0, 0f0) — это явное указание типа Float32 для оптимизации производительности. В Julia по умолчанию числа с плавающей точкой (6.0) имеют тип Float64 (двойная точность). Использование Float32 даёт два ключевых преимущества:

Экономия памяти — каждый Float32 занимает 4 байта вместо 8 байт у Float64
Ускорение вычислений

Для визуализации и физических симуляций точности Float32 (±7 десятичных цифр) полностью достаточно, что позволяет обрабатывать больше частиц или кадров анимации за меньшее время.

function generate_same_particles()
    Random.seed!(42)
    colors = [:red, :blue, :green, :orange, :purple, :cyan]
    particles = Particle[]
    for i in 1:6
        push!(particles, Particle(
            rand(Float32) * 6f0 - 3f0,  # x: -3 до 3
            rand(Float32) * 2f0 + 2f0,  # y: 2 до 4
            rand(Float32) * 2f0 - 1f0,  # vx: -1 до 1
            0f0,                        # vy: 0
            colors[i]                   # фиксированные цвета
        ))
    end
    return particles
end

generate_same_particles (generic function with 1 method)

Функция simulate_planet_same_particles представляет собой ядро физической симуляции, реализующее численное интегрирование движения частиц под действием гравитации на конкретной планете. Она принимает три ключевых параметра: значение гравитационного ускорения g, массив начальных частиц initial_particles и параметры временной дискретизации — шаг dt и количество шагов steps.

В начале функции создаётся глубокая копия исходных частиц через deepcopy, что гарантирует независимость симуляций для разных планет при использовании одинаковых начальных условий. Для хранения полных траекторий движения инициализируются массивы x_traj и y_traj, размер которых соответствует общему числу временных срезов. Основной расчёт выполняется в двойном цикле: внешний проходит по временным шагам, внутренний — по всем частицам. Для каждой частицы сначала фиксируются её текущие координаты, после чего, если это не последний шаг, применяется физическая модель. Модель включает два компонента: гравитационное ускорение, которое увеличивает вертикальную скорость частицы согласно формуле p.vy -= g * dt, и кинематическое обновление позиции через p.x += p.vx * dt и p.y += p.vy * dt.

Особое внимание уделяется обработке граничных условий. При столкновении с полом (когда координата y становится отрицательной) частица отражается с потерей 20% вертикальной скорости и 10% горизонтальной, что моделирует неупругий удар. Аналогично, при достижении боковых стен частица отражается от них, теряя 10% горизонтальной скорости. Эти коэффициенты обеспечивают реалистичное затухание движения со временем.

После обработки всех частиц на текущем шаге их координаты сохраняются в соответствующие массивы траекторий. По завершении цикла функция возвращает три массива: последовательности X- и Y-координат для всех частиц на всех временных шагах, а также список их цветов для последующей визуализации. Эта структура данных позволяет не только воспроизвести анимацию движения, но и проанализировать эволюцию системы частиц под заданным гравитационным воздействием.

function simulate_planet_same_particles(g::Float32, initial_particles, dt::Float32, steps::Int)
    particles = deepcopy(initial_particles)
    n = length(particles)
    x_traj = Vector{Vector{Float32}}(undef, steps+1)
    y_traj = Vector{Vector{Float32}}(undef, steps+1)
    colors = [p.color for p in particles]
    for step in 0:steps
        x_vals = Vector{Float32}(undef, n)
        y_vals = Vector{Float32}(undef, n)
        for i in 1:n
            p = particles[i]
            x_vals[i] = p.x
            y_vals[i] = p.y
            if step < steps
                p.vy -= g * dt
                p.x += p.vx * dt
                p.y += p.vy * dt
                if p.y < 0
                    p.y = 0
                    p.vy = -0.8f0 * p.vy
                    p.vx *= 0.9f0
                end
                if p.x > 4
                    p.x = 4
                    p.vx = -0.9f0 * p.vx
                elseif p.x < -4
                    p.x = -4
                    p.vx = -0.9f0 * p.vx
                end
            end
        end
        x_traj[step+1] = copy(x_vals)
        y_traj[step+1] = copy(y_vals)
    end
    return x_traj, y_traj, colors
end

simulate_planet_same_particles (generic function with 1 method)

Последний блок кода организует полный цикл эксперимента — от настройки параметров до генерации итоговой анимации. Он начинается с инициализации ключевых переменных: количество частиц n_particles устанавливается равным 6, шаг времени dt фиксируется в 0.04 секунды (с указанием типа Float32), а общее время моделирования total_time составляет 10 секунд. Параметр skip_frames со значением 2 определяет, что для анимации будет использоваться каждый второй кадр, что сокращает размер выходного файла без существенной потери информативности. Список planets включает девять небесных тел для сравнительного анализа.

На основе заданного общего времени и шага интегрирования вычисляется количество временных шагов steps по формуле Int(floor(total_time / dt)). Это гарантирует, что симуляция будет выполнена ровно на указанный промежуток времени. Затем с помощью функции generate_same_particles() создаётся эталонный набор из шести частиц с фиксированными начальными условиями — это основа для корректного сравнения влияния разной гравитации.

Далее запускается цикл расчёта траекторий для каждой планеты. Для каждого небесного тела из словаря PLANET_GRAVITY извлекается соответствующее значение ускорения свободного падения g, после чего вызывается функция simulate_planet_same_particles. Она возвращает массивы траекторий, цвета частиц и значение гравитации, которые сохраняются в списке planet_data. Таким образом формируется полный набор данных для визуализации.

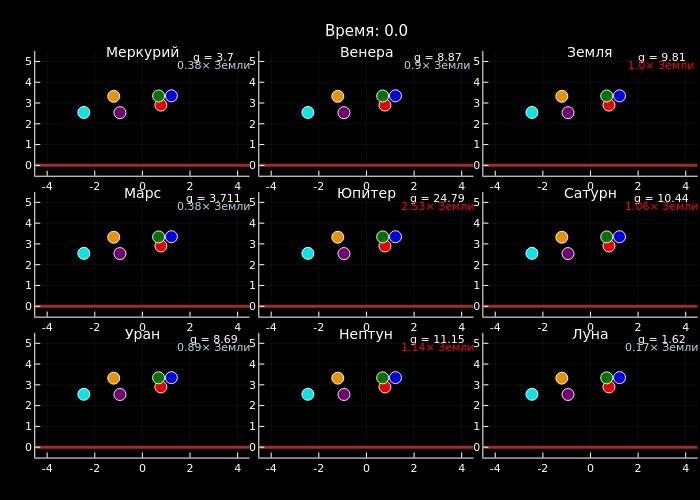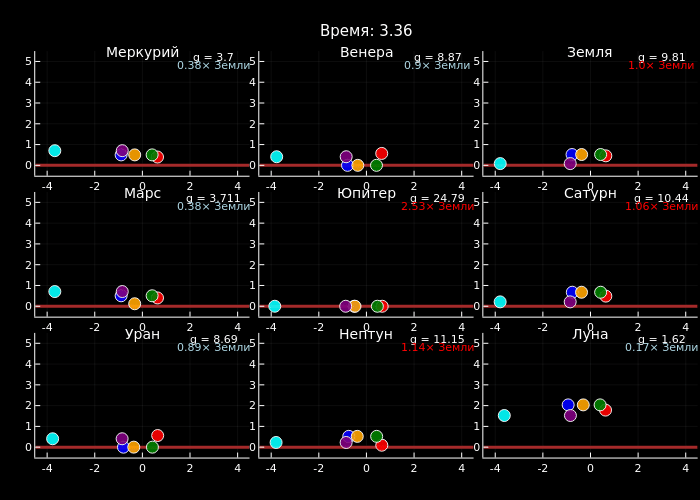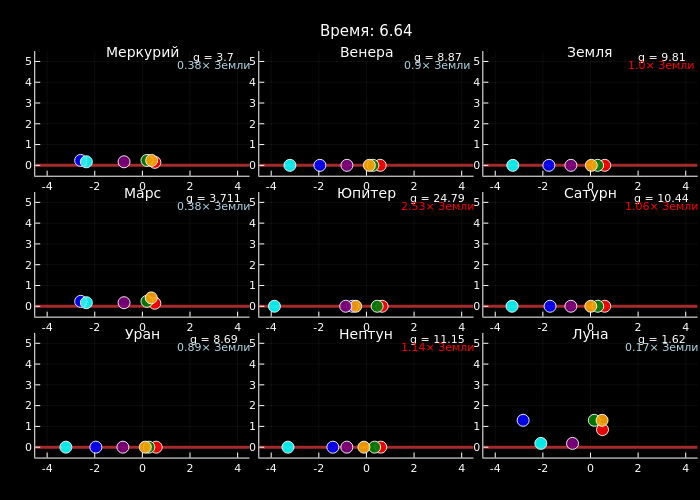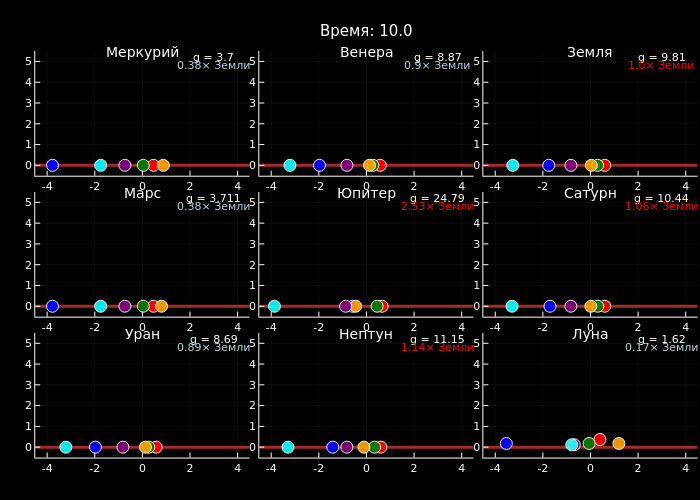
Финальная часть блока отвечает за создание анимации с использованием макроса @animate из библиотеки Plots. Внешний цикл перебирает кадры с учётом пропуска, вычисляя текущее модельное время t. Для каждого момента времени строится общий график с компоновкой 3×3, где каждый субграфик соответствует одной планете. Настройки включают чёрный фон для контраста, общий заголовок и динамически обновляемое время в заголовке.

Внутренний цикл обрабатывает каждый субграфик: устанавливаются фиксированные границы осей, добавляется коричневая линия, изображающая поверхность планеты, и отображаются частицы в их текущей позиции с сохранением цветовой схемы. Важный элемент — информационные аннотации: абсолютное значение гравитации и его отношение к земному (последнее выделяется цветом — красным для значений выше земного и голубым для меньших).

После генерации всех кадров анимация сохраняется в файл particles_all_planets.gif со скоростью 22 кадра в секунду. В результате получается наглядная сравнительная визуализация, демонстрирующая, как одна и та же система частиц ведёт себя в различных гравитационных условиях Солнечной системы.

println("Тест для всех планет")
dt = 0.04f0
total_time = 10.0f0
skip_frames = 2
planets = ["Меркурий", "Венера", "Земля", "Марс", 
           "Юпитер", "Сатурн", "Уран", "Нептун", "Луна"]
steps = Int(floor(total_time / dt))

println("\nГенерирация частиц...")
same_particles = generate_same_particles()

println("Рассчёт траекторий...")
planet_data = []
for planet in planets
    g = Float32(PLANET_GRAVITY[planet])
    data = simulate_planet_same_particles(g, same_particles, dt, steps)
    push!(planet_data, (data..., g))
end

println("Создаие анимации...")
anim = @animate for frame in 0:skip_frames:steps
    t = frame * dt
    plot(layout = (3, 3), 
         size = (1200, 900),
         title = "Одинаковые частицы на разных планетах",
         titlefontsize = 14,
         plot_title = "Время: $(round(t, digits=2))",
         plot_titlefontsize = 11,
         legend = false,
         bg = :black)
    
    for (idx, planet) in enumerate(planets)
        x_traj, y_traj, colors, g = planet_data[idx]
        actual_frame = min(frame + 1, length(x_traj))
        plot!(subplot = idx,
              xlim = (-4.5, 4.5),
              ylim = (-0.5, 5.5),
              aspect_ratio = :equal,
              title = planet,
              titlefontsize = 10)
        plot!([-4.5, 4.5], [0, 0], 
              linewidth = 3, 
              color = :brown,
              subplot = idx)
        scatter!(x_traj[actual_frame], y_traj[actual_frame],
                markersize = 6,
                markercolor = colors,
                markerstrokecolor = :white,
                alpha = 0.9,
                subplot = idx)

        gravity_ratio = round(g / 9.81, digits=2)
        color_code = g > 9.81 ? :red : :lightblue
        
        annotate!(3.0, 5.2, 
                 text("g = $(g)", 8, :white),
                 subplot = idx)
        annotate!(3.0, 4.8,
                 text("$(gravity_ratio)× Земли", 8, color_code),
                 subplot = idx)
    end
end
gif(anim, "particles_all_planets.gif", fps = 22)

Тест для всех планет

Генерирация частиц...
Рассчёт траекторий...
Создаие анимации...

Вывод

Данный пример демонстрирует, как гравитация определяет динамику физических систем: используя численное интегрирование и оптимизированные вычисления, мы создали сравнительную симуляцию движения частиц на девяти небесных телах, где чётко видно, что на Юпитере частицы падают и отскакивают значительно быстрее, чем на Луне или Марсе.

Моделирование движения частиц

Моделирование движения частиц, визуализация гравитации

Вывод

Тип

Краткое описание

Связанные материалы

Теги

Категории

Языки

Форматы

Уровень

Статус

Опубликовано

Обновлено

Источник