Моделирование эффекта Джанибекова

В данном примере будет показано моделирование эффекта Джанибекова - нестабильного вращения твердого тела вокруг средней оси инерции. Модель демонстрирует, как небольшое возмущение при вращении вокруг промежуточной оси приводит к периодическому "перевороту" объекта в пространстве.

Эффект Джанибекова проявляется при вращении асимметричного твердого тела вокруг оси с промежуточным моментом инерции. Согласно теореме о промежуточной оси, такое вращение неустойчиво - малейшее возмущение приводит к периодическому "перевороту" объекта.

Условие возникновения: I₁ < I₂ < I₃, где I₂ - момент инерции относительно средней оси.

Начальное возмущение: .

Схема модели:

Для реализации модели вращения в данном примере используется блок Engee Function, в котором, с помощью кода, были реализованы уравнения Эйлера для свободного вращения:

Также в этом блоке описывается кинематика кватернионов:

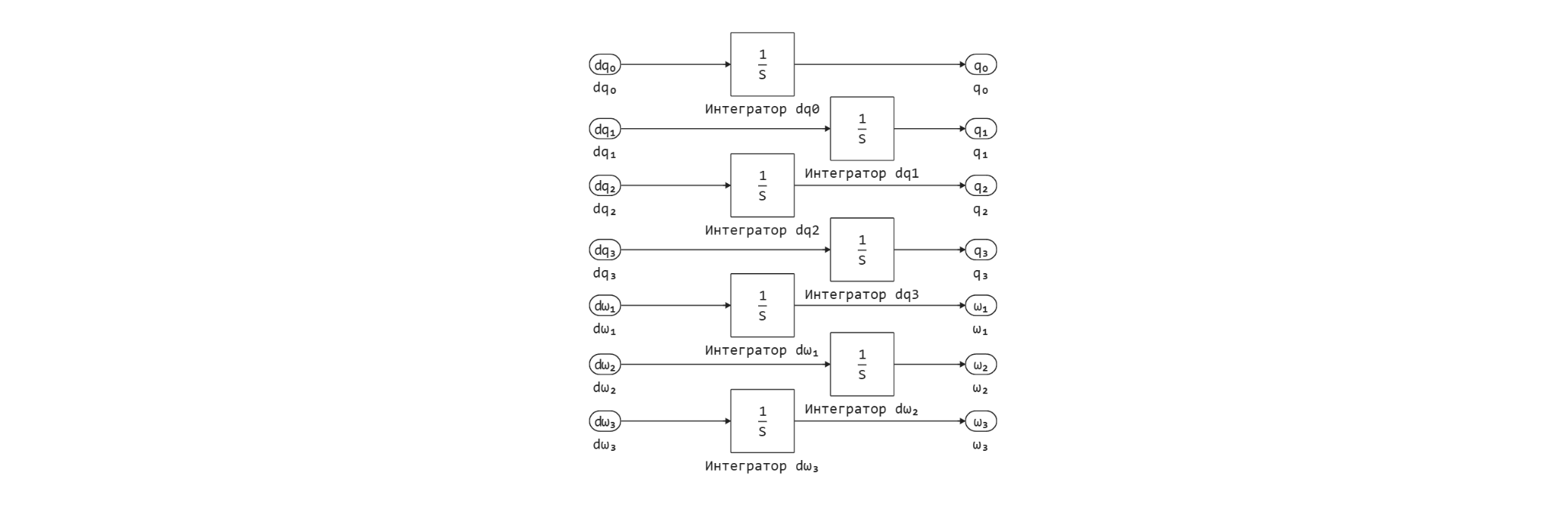
На вход блока подаются состояния интегралы от производных кватернионов и угловых скоростей, рассчитываемые в блоке Интегрирование, имеющим следующее устройство:

С помощью блоков шин сигналы компонуются для дальнейшего использования. Из Шины 3 сигнал идёт в блок, в котором шина преобразуется в вектор и, затем, подаётся на вход блока Преобразования кватерниона в матрицу поворота.

Определение функции для загрузки и запуска модели:

function start_model_engee()
    try
        engee.close("dzhanibekov_effect", force=true) # закрытие модели 
        catch err # в случае, если нет модели, которую нужно закрыть и engee.close() не выполняется, то будет выполнена её загрузка после catch
            m = engee.load("$(@__DIR__)/dzhanibekov_effect.engee") # загрузка модели
        end;

    try
        engee.run(m) # запуск модели
        catch err # в случае, если модель не загружена и engee.run() не выполняется, то будут выполнены две нижние строки после catch
            m = engee.load("$(@__DIR__)/dzhanibekov_effect.engee") # загрузка модели
            engee.run(m) # запуск модели
        end
end

start_model_engee (generic function with 1 method)

Запуск симуляции

start_model_engee();

Вывод данных в отдельную переменную:

result = collect(simout["dzhanibekov_effect/Преобразование кватерниона
 в матрицу поворота.DCM"]);

Вывод данных в отдельные переменные для их анализа и построения визуализации:

time_ = result[:,1]
R_hist = result[:,2];

Определение функции для создания Т-образной геометрической фигуры:

function create_t_figure()
    vertical = [[0, 0], [-0.5, 0.5], [0, 0]]
    horizontal = [[-0.6, 0.6], [0.5, 0.5], [0, 0]]
    return (vertical, horizontal)
end

create_t_figure (generic function with 1 method)

Определение функции для создания анимации движения тела:

using Printf
function create_djanibekov_animation_plots(R_hist, time_)
    gr()
    # Создаем T-образную фигуру
    t_figure = create_t_figure()
    vertical, horizontal = t_figure
    
    # Функция для преобразования точек с помощью матрицы вращения
    function rotate_points(points, R)
        x, y, z = points
        n = length(x)
        rotated = zeros(3, n)
        for i in 1:n
            rotated[:, i] = R * [x[i], y[i], z[i]]
        end
        return rotated[1, :], rotated[2, :], rotated[3, :]
    end
    
    # Создаем анимацию
    anim = @animate for i in 1:40:length(R_hist)
        R = R_hist[i]
        
        # Применяем вращение к фигуре
        v_rot = rotate_points(vertical, R)
        h_rot = rotate_points(horizontal, R)
        gr()
        # Создаем 3D график
        p = plot3d(
            v_rot..., 
            linewidth=3,
            linecolor=:red,
            label="",
            xlim=(-1, 1),
            ylim=(-1, 1),
            zlim=(-1, 1),
            title="Эффект Джанибекова (t = $(@sprintf("%.2f", time_[i])) с)",
            xlabel="X",
            ylabel="Y",
            zlabel="Z",
            aspect_ratio=:equal,
            camera=(30, 30)
        )
        
        plot3d!(
            h_rot...,
            linewidth=3,
            linecolor=:blue,
            label=""
        )
        
        # Добавляем сферу в центре
        scatter3d!([0], [0], [0], markersize=4, markercolor=:gray, label="")
    end
    
    # Сохраняем анимацию в GIF
    output_path = "djanibekov_effect_plots.gif"
    
    println("Анимация сохранена в файл: ", output_path)
    return gif(anim, output_path, fps=25)
end

create_djanibekov_animation_plots (generic function with 1 method)

Создание анимации движения тела и её визуализация:

anim = create_djanibekov_animation_plots(R_hist, time_)

Анимация сохранена в файл: djanibekov_effect_plots.gif

[ Info: Saved animation to /user/djanibekov_effect_plots.gif

w1 = collect(simout["dzhanibekov_effect/Интегрирование.ω₁"])
w2 = collect(simout["dzhanibekov_effect/Интегрирование.ω₂"])
w3 = collect(simout["dzhanibekov_effect/Интегрирование.ω₃"]);

plotlyjs()
plot(w1[:, 1], w1[:, 2], label="Угловая скорость вокруг оси X", lw=2)
plot!(w2[:, 1], w2[:, 2], label="Угловая скорость вокруг оси Y", lw=2)
plot!(w3[:, 1], w3[:, 2], label="Угловая скорость вокруг оси Z", lw=2)

Переворот можно отследить на графике по смене знака угловой скорости вокруг оси Y, это происходит каждые 4 секунды.

Выводы:

В данном примере была продемонстрирована модель эффекта Джанибекова. Модель можно модифицировать и использовать в различных областях для задач наведения, слежения за целями и для управления ориентацией манипуляторов.

Эффект Джанибекова

Моделирование эффекта Джанибекова

Схема модели:

Определение функции для загрузки и запуска модели:

Запуск симуляции

Выводы:

Тип

Краткое описание

Связанные материалы

Теги

Категории

Языки

Форматы

Уровень

Статус

Опубликовано

Обновлено

Источник