Моделирование Солнечной системы.

В этой статье мы рассмотрим, как можно создать полноценную модель Солнечной системы, которая не только демонстрирует гравитационные взаимодействия, но и позволяет исследовать последствия изменения ключевых параметров системы — например, массы центральной звезды. Представленная реализация расширяет классические задачи небесной механики, включая термодинамические аспекты, что позволяет изучать комплексное влияние изменения массы Солнца как на орбитальную динамику, так и на климатические условия планет.

Ключевые аспекты реализации:

Реализация закона всемирного тяготения Ньютона для системы из 9 взаимодействующих тел (Солнце + 8 планет), где каждое тело влияет на все остальные, а не только на центральное.
Модель включает фундаментальное соотношение масса-светимость для звёзд (L ~ M³·⁵), что позволяет оценить, как изменение массы Солнца влияет на его энерговыделение. На основе этой зависимости рассчитываются равновесные температуры планет в градусах Цельсия.
Создана отдельная система расчёта и визуализации, показывающая, как температура планет изменяется при варьировании массы Солнца в диапазоне от 1 до 10⁷ солнечных масс. Результаты представлены в виде графиков и таблиц с температурными маркерами (🔥 для температур выше 1000°C, ❄ — ниже 0°C).
Использование метода Эйлера для решения уравнений движения с адаптивным шагом, обеспечивающим баланс между точностью и производительностью при моделировании на временных масштабах до 10 лет.

Этот проект служит отличной отправной точкой для изучения Engee, демонстрируя, как язык программирования справляется с задачами, требующими вычислительной эффективности, ясного кода и наглядной визуализации. В следующих разделах мы подробно разберём архитектуру кода, физические основы, реализацию температурных расчётов и образовательные аспекты этой модели, а также рассмотрим, как подобные симуляции могут быть использованы в учебном процессе и научно-популярных проектах.

Теперь перейдём к анализу блоков кода и начнём с констант применяемых в работе.

Гравитационная постоянная (G = 6.67430×10⁻¹¹ м³·с⁻²·кг⁻¹) — это фундаментальная физическая константа, определяющая силу гравитационного притяжения между телами, обладающими массой. В классической механике Ньютона она входит в закон всемирного тяготения, согласно которому сила притяжения между двумя телами пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между их центрами. Именно эта константа связывает геометрию пространства-времени с распределением материи, определяя интенсивность гравитационного взаимодействия в нерелятивистском пределе. В нашем моделировании гравитационная постоянная позволяет рассчитать ускорение, с которым Солнце притягивает планеты, и наоборот, формируя реалистичную орбитальную динамику.

Астрономическая единица (AU = 1.496×10¹¹ метров) — это исторически сложившаяся единица измерения расстояний в астрономии, приблизительно равная среднему расстоянию от Земли до Солнца. Введение этой константы в модель служит двум важным целям. Во-первых, она обеспечивает естественный масштаб для представления орбит планет, поскольку большие полуоси их орбит традиционно выражаются в астрономических единицах. Во-вторых, использование AU упрощает восприятие и настройку параметров модели, так как исследователи привыкли оперировать этими величинами в астрономическом контексте, а не в абсолютных метрических единицах.

Постоянная Стефана-Больцмана (σ = 5.670374419×10⁻⁸ Вт·м⁻²·К⁻⁴) — фундаментальная физическая константа, описывающая закон Стефана-Больцмана для излучения абсолютно чёрного тела. Согласно этому закону, полная энергия, излучаемая единицей поверхности абсолютно чёрного тела в единицу времени, пропорциональна четвёртой степени его термодинамической температуры. В контексте нашей модели эта константа является ключевым элементом для расчёта равновесной температуры планет. Она позволяет перейти от светимости Солнца (определяемой через массу) к тепловому потоку, достигающему планеты, и далее — к расчётной температуре её поверхности с учётом альбедо. Именно благодаря этой константе модель приобретает термодинамическую составляющую, связывающую гравитационную динамику с климатическими условиями на планетах.

const G = 6.67430e-11        # Гравитационная постоянная
const AU = 1.496e11          # Астрономическая единица (м)
const YEAR = 365.25 * 86400.0 # Год в секундах
const SOLAR_MASS = 1.989e30   # Масса Солнца (кг)
const SOLAR_RADIUS = 6.957e8  # Радиус Солнца (м)
const STEFAN_BOLTZMANN = 5.670374419e-8

5.670374419e-8

Структура Body представляет собой фундаментальный элемент модели, инкапсулирующий полный физический и визуальный профиль небесного тела. Будучи мутабельной (изменяемой), она позволяет динамически обновлять состояние объектов на каждом шаге симуляции, отражая их эволюцию во времени.

Включает три категории параметров:

динамические характеристики (позиция x, y, скорость vx, vy, ускорение ax, ay)
физические свойства (масса mass, физический и орбитальный радиусы)
атрибуты для визуализации и анализа (имя, цвет, температура).

Особенно важно поле temperature, которое вычисляется на основе светимости Солнца и расстояния до тела.

mutable struct Body
    name::String
    mass::Float64           # Масса (кг)
    radius::Float64         # Физический радиус (м)
    orbit_radius::Float64   # Начальный орбитальный радиус (м)
    color::Symbol
    x::Float64              # Положение X (м)
    y::Float64              # Положение Y (м)
    vx::Float64             # Скорость X (м/с)
    vy::Float64             # Скорость Y (м/с)
    ax::Float64             # Ускорение X (м/с²)
    ay::Float64             # Ускорение Y (м/с²)
    temperature::Float64    # Равновесная температура (°C)
end

Массив planets_data содержит исходные астрофизические параметры и визуальные атрибуты восьми планет Солнечной системы, которые служат начальными условиями для создания объектов типа Body в симуляции.

planets_data = [
    ("Mercury", 3.285e23, 2.4397e6, 0.39*AU, :orange),
    ("Venus", 4.867e24, 6.0518e6, 0.72*AU, :green),
    ("Earth", 5.972e24, 6.371e6, 1.0*AU, :blue),
    ("Mars", 6.39e23, 3.3895e6, 1.52*AU, :red),
    ("Jupiter", 1.898e27, 6.9911e7, 5.2*AU, :brown),
    ("Saturn", 5.683e26, 5.8232e7, 9.58*AU, :gold),
    ("Uranus", 8.681e25, 2.5362e7, 19.22*AU, :cyan),
    ("Neptune", 1.024e26, 2.4622e7, 30.05*AU, :darkblue)
]

8-element Vector{Tuple{String, Float64, Float64, Float64, Symbol}}:
 ("Mercury", 3.285e23, 2.4397e6, 5.8344e10, :orange)
 ("Venus", 4.867e24, 6.0518e6, 1.07712e11, :green)
 ("Earth", 5.972e24, 6.371e6, 1.496e11, :blue)
 ("Mars", 6.39e23, 3.3895e6, 2.27392e11, :red)
 ("Jupiter", 1.898e27, 6.9911e7, 7.7792e11, :brown)
 ("Saturn", 5.683e26, 5.8232e7, 1.433168e12, :gold)
 ("Uranus", 8.681e25, 2.5362e7, 2.875312e12, :cyan)
 ("Neptune", 1.024e26, 2.4622e7, 4.49548e12, :darkblue)

Функция solar_luminosity реализует астрофизический закон «масса-светимость» (L ∼ M³·⁵), преобразуя относительное изменение массы Солнца в соответствующий множитель для его энерговыделения. Функция equilibrium_temperature_c на основе этой светимости и расстояния до планеты рассчитывает её равновесную температуру в градусах Цельсия, используя модель поглощения и переизлучения энергии с учётом альбедо и закона Стефана-Больцмана.

function solar_luminosity(mass_factor)
    return mass_factor^3.5  # L ~ M^3.5
end

function equilibrium_temperature_c(luminosity_factor, distance_au)
    # Упрощённая формула для температуры в градусах Цельсия
    albedo = 0.3
    solar_constant = 1361.0  # Вт/м² для Земли
    # Температура в Кельвинах
    temp_k = (solar_constant * luminosity_factor * (1 - albedo) / 
            (4 * STEFAN_BOLTZMANN))^0.25
    # Корректировка для расстояния и перевод в Цельсий
    return (temp_k / sqrt(distance_au)) - 273.15
end

equilibrium_temperature_c (generic function with 1 method)

Функция create_temperature_stats проводит комплексный термодинамический анализ, рассчитывая равновесные температуры всех планет для широкого диапазона масс Солнца (от 1 до 10⁷ солнечных масс), создаёт два типа графиков — зависимость температуры от массы звезды и от расстояния до неё, выводит таблицу результатов и сохраняет оба графика в файлы для дальнейшего использования, выполняя роль автономного модуля визуализации климатических сценариев.

function create_temperature_stats()
    sun_mass_factors = [1, 10, 100, 1000, 1e4, 1e5, 1e6, 1e7]
    planets_info = [
        ("Mercury", 0.39, :orange),
        ("Venus", 0.72, :green),
        ("Earth", 1.0, :blue),
        ("Mars", 1.52, :red),
        ("Jupiter", 5.2, :brown),
        ("Saturn", 9.58, :gold),
        ("Uranus", 19.22, :cyan),
        ("Neptune", 30.05, :darkblue)
    ]
    
    # Расчёт температур
    temperatures = Dict()
    for (name, distance_au, color) in planets_info
        temps = Float64[]
        for mass_factor in sun_mass_factors
            lum_factor = solar_luminosity(mass_factor)
            temp_c = equilibrium_temperature_c(lum_factor, distance_au)
            push!(temps, temp_c)
        end
        temperatures[name] = temps
    end

    p1 = plot(size=(1000, 600), 
              title="Зависимость температуры планет от массы Солнца",
              xlabel="Масса Солнца (в солнечных массах)",
              ylabel="Температура (°C)",
              xscale=:log10,
              yscale=:linear,
              grid=true, gridstyle=:dash,
              legend=:topleft,
              framestyle=:box)

    for (name, _, color) in planets_info
        plot!(p1, sun_mass_factors, temperatures[name], 
              label=name, color=color, linewidth=2, marker=:circle)
    end
    hline!(p1, [0], label="Температура замерзания воды", color=:blue, linestyle=:dash)
    hline!(p1, [100], label="Температура кипения воды", color=:red, linestyle=:dash)
    annotate!(p1, 1e5, 1500, text("Экстремальные условия", 10, :gray))

    p2 = plot(size=(1000, 600),
              title="Температура планет в зависимости от расстояния",
              xlabel="Расстояние от Солнца (AU)",
              ylabel="Температура (°C)",
              xscale=:log10,
              yscale=:linear,
              grid=true,
              legend=:topright)
    distances = [d for (_, d, _) in planets_info]
    planet_names = [n for (n, _, _) in planets_info]
    
    for (i, mass_factor) in enumerate([1, 10, 100, 1000])
        temps = [temperatures[name][i] for name in planet_names]
        plot!(p2, distances, temps,
              label="M☉ = $(Int(mass_factor))×",
              linewidth=2,
              marker=:circle)
    end
    display(p1)
    display(p2)

    println("\n" * "="^70)
    println("ТЕМПЕРАТУРЫ ПЛАНЕТ ПРИ РАЗНОЙ МАССЕ СОЛНЦА (°C)")
    println("="^70)
    print("Масса Солнца: ")
    for mf in sun_mass_factors
        print(lpad("$(Int(mf))×", 10))
    end
    println()
    
    for (name, _, _) in planets_info
        print(rpad(name, 12))
        for temp in temperatures[name]
            if temp > 1000
                print(lpad("🔥$(round(Int, temp))", 10))
            elseif temp > 100
                print(lpad("$(round(Int, temp))", 10))
            elseif temp > 0
                print(lpad("$(round(Int, temp))", 10))
            else
                print(lpad("❄$(round(Int, temp))", 10))
            end
        end
        println()
    end
    println("="^70)
    
    savefig(p1, "temperature_vs_mass.png")
    savefig(p2, "temperature_vs_distance.png")
    return temperatures
end

create_temperature_stats (generic function with 1 method)

Функция calculate_initial_velocity вычисляет начальную орбитальную скорость небесного тела, обеспечивающую его движение по круговой траектории вокруг Солнца, исходя из заданного положения тела и массы центральной звезды в соответствии с классической механикой Ньютона.

function calculate_initial_velocity(sun_mass, body_x, body_y)
    r = sqrt(body_x^2 + body_y^2)
    v_circ = sqrt(G * sun_mass / r)
    return (-body_y / r * v_circ, body_x / r * v_circ)
end

calculate_initial_velocity (generic function with 1 method)

Далее представлена основная функция simulate_solar_system, он инициализирует и выполняет полный цикл моделирования гравитационной динамики и теплового состояния системы. Она начинается с создания массива тел bodies, включающего Солнце с массой, скорректированной на заданный коэффициент sun_mass_factor, и все планеты с рассчитанными начальными скоростями для круговых орбит. Параметры интегрирования, такие как шаг по времени dt и общее число шагов n_steps, преобразуют входные астрономические величины (годы, дни) в вычислительные интервалы, подготавливая систему для численного решения.

Внутри основного цикла функция на каждом шаге пересчитывает гравитационные ускорения для всех пар тел, используя закон Ньютона, и обновляет их скорости и координаты методом Эйлера. Одновременно для планет вычисляется текущая равновесная температура на основе светимости Солнца и расстояния до него, что добавляет термодинамический контекст к чисто механической симуляции. С заданной периодичностью состояние системы сохраняется для последующей визуализации.

По завершении расчётов функция создаёт анимационный GIF-файл, в котором кадры последовательно отображают эволюцию системы: Солнце в виде минималистичной точки в центре, планеты, окрашенные в соответствии с их температурой (от холодного голубого до раскалённого красного), и едва заметную прозрачную зону для масштаба. Заголовок анимации динамически отражает ключевые параметры, включая температуру Земли, обеспечивая наглядное представление результатов вычислительного эксперимента по изменению массы центральной звезды.

function simulate_solar_system(sun_mass_factor=1.0; years=10, step_days=5, filename="solar_system.gif")
    sun_mass = SOLAR_MASS * sun_mass_factor
    sun_luminosity = solar_luminosity(sun_mass_factor)
    bodies = [Body("Sun", sun_mass, SOLAR_RADIUS, 0.0, :yellow, 
                   0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 5778.0 - 273.15)]
    
    for (name, mass, radius, orbit_r, color) in planets_data
        vx, vy = calculate_initial_velocity(sun_mass, orbit_r, 0.0)
        body = Body(name, mass, radius, orbit_r, color, 
                    orbit_r, 0.0, vx, vy, 0.0, 0.0, 0.0)
        push!(bodies, body)
    end
    
    dt = step_days * 86400.0
    n_steps = Int(round(years * YEAR / dt))
    frames_per_gif = 150
    step_skip = max(1, n_steps ÷ frames_per_gif)
    positions_history = []

    function compute_accelerations!(bodies)
        for body in bodies
            body.ax = 0.0
            body.ay = 0.0
        end
        
        n = length(bodies)
        for i in 1:n
            for j in i+1:n
                dx = bodies[j].x - bodies[i].x
                dy = bodies[j].y - bodies[i].y
                r_sq = dx^2 + dy^2
                r = sqrt(r_sq)
                
                if r > 1e-6
                    force = G * bodies[i].mass * bodies[j].mass / r_sq
                    ax_i = force * dx / (r * bodies[i].mass)
                    ay_i = force * dy / (r * bodies[i].mass)
                    ax_j = -force * dx / (r * bodies[j].mass)
                    ay_j = -force * dy / (r * bodies[j].mass)
                    
                    bodies[i].ax += ax_i
                    bodies[i].ay += ay_i
                    bodies[j].ax += ax_j
                    bodies[j].ay += ay_j
                end
            end
        end
    end

    println("Симуляция: M☉ = $(sun_mass_factor)×, $(years) лет, шаг $(step_days) дней")
    for step in 0:n_steps
        if step % step_skip == 0
            pos = []
            for body in bodies
                if body.mass > 0.0
                    if body.name != "Sun"
                        dist_au = sqrt(body.x^2 + body.y^2) / AU
                        body.temperature = equilibrium_temperature_c(sun_luminosity, dist_au)
                    end
                    push!(pos, (body.x, body.y, body.color, body.name, body.temperature))
                end
            end
            push!(positions_history, pos)
        end
        step == n_steps && break
        compute_accelerations!(bodies)
        for body in bodies
            body.vx += body.ax * dt
            body.vy += body.ay * dt
            body.x += body.vx * dt
            body.y += body.vy * dt
        end
    end
    
    max_dist = 1.2 * maximum([b.orbit_radius for b in bodies if b.name != "Sun"])
    anim = @animate for (frame, positions) in enumerate(positions_history)
        time_years = frame * step_skip * dt / YEAR
        earth_temp = 0.0
        for (x, y, color, name, temp) in positions
            if name == "Earth"
                earth_temp = temp
                break
            end
        end
        
        p = plot(size=(1000, 800), aspect_ratio=:equal,
                 xlim=(-max_dist, max_dist), ylim=(-max_dist, max_dist),
                 title="M☉ = $(sun_mass_factor)× | L☉ = $(round(sun_luminosity, digits=1))× | $(round(time_years, digits=1)) лет | T♁ = $(round(earth_temp, digits=1))°C",
                 legend=:none, framestyle=:box, 
                 background_color=:black,
                 titlefontsize=12)
        scatter!(p, [0.0], [0.0], 
                markersize=2, color=:yellow, marker=:circle, 
                markerstrokewidth=0, markercolor=:yellow, alpha=0.8)

        theta = range(0, 2π, length=100)
        zone_radius = 0.05 * AU
        circle_x = zone_radius .* cos.(theta)
        circle_y = zone_radius .* sin.(theta)
        plot!(p, circle_x, circle_y, color=:lightgray, linewidth=0.5, alpha=0.15, label="")

        for (x, y, color, name, temp) in positions
            if name != "Sun"
                body = first([b for b in bodies if b.name == name])
                size_factor = 5 + 2 * log10(body.mass / 5.972e24)
                marker_color = if temp > 1000
                    :red
                elseif temp > 100
                    :orange
                elseif temp > 0
                    :green
                else
                    :lightblue
                end
                scatter!(p, [x], [y], 
                        markersize=max(3, size_factor),
                        color=marker_color, marker=:circle, 
                        markerstrokewidth=1)
            end
        end
        plot!(p, [max_dist*0.7, max_dist*0.7 + AU], [max_dist*0.9, max_dist*0.9],
              color=:white, linewidth=2)
        annotate!(p, max_dist*0.7 + AU/2, max_dist*0.88, 
                 text("1 AU", 10, :white))
    end
    gif(anim, filename, fps=20)
    println("Анимация сохранена: $filename")
    return bodies
end

simulate_solar_system (generic function with 2 methods)

Запустим тест и посмотрим на результаты.

create_temperature_stats()

======================================================================
ТЕМПЕРАТУРЫ ПЛАНЕТ ПРИ РАЗНОЙ МАССЕ СОЛНЦА (°C)
======================================================================
Масса Солнца:         1×       10×      100×     1000×    10000×   100000×  1000000× 10000000×
Mercury            135    🔥2784   🔥22651  🔥171632 🔥1288833 🔥9666662🔥72491514🔥543611440
Venus               27    🔥1977   🔥16598  🔥126246  🔥948484 🔥7114398🔥53352237🔥400087115
Earth             ❄-19    🔥1636   🔥14043  🔥107082  🔥804774 🔥6036726🔥45270833🔥339485133
Mars              ❄-67    🔥1275   🔥11339   🔥86803  🔥652706 🔥4896380🔥36719443🔥275358752
Jupiter          ❄-162       564    🔥6005   🔥46805  🔥352763 🔥2647126🔥19852420🔥148873926
Saturn           ❄-191       344    🔥4352   🔥34412  🔥259826 🔥1950193🔥14626157🔥109682483
Uranus           ❄-215       162    🔥2992   🔥24214  🔥183357 🔥1376760🔥10326019🔥77435995
Neptune          ❄-227        75    🔥2338   🔥19311  🔥146585 🔥1101010 🔥8258183🔥61929412
======================================================================

Dict{Any, Any} with 8 entries:
  "Neptune" => [-226.709, 75.1062, 2338.4, 19310.7, 1.46585e5, 1.10101e6, 8.258…
  "Mercury" => [134.501, 2783.8, 22650.8, 171632.0, 1.28883e6, 9.66666e6, 7.249…
  "Earth"   => [-18.5719, 1635.92, 14042.8, 1.07082e5, 8.04774e5, 6.03673e6, 4.…
  "Saturn"  => [-190.9, 343.641, 4352.13, 34411.6, 2.59826e5, 1.95019e6, 1.4626…
  "Jupiter" => [-161.51, 564.031, 6004.82, 46805.0, 3.52763e5, 2.64713e6, 1.985…
  "Venus"   => [26.8732, 1976.71, 16598.4, 1.26246e5, 9.48484e5, 7.1144e6, 5.33…
  "Uranus"  => [-215.081, 162.306, 2992.31, 24214.3, 1.83357e5, 1.37676e6, 1.03…
  "Mars"    => [-66.6599, 1275.31, 11338.6, 86803.0, 652706.0, 4.89638e6, 3.671…

simulate_solar_system(1.0, years=10, step_days=3, filename="normal_sun.gif");

Симуляция: M☉ = 1.0×, 10 лет, шаг 3 дней
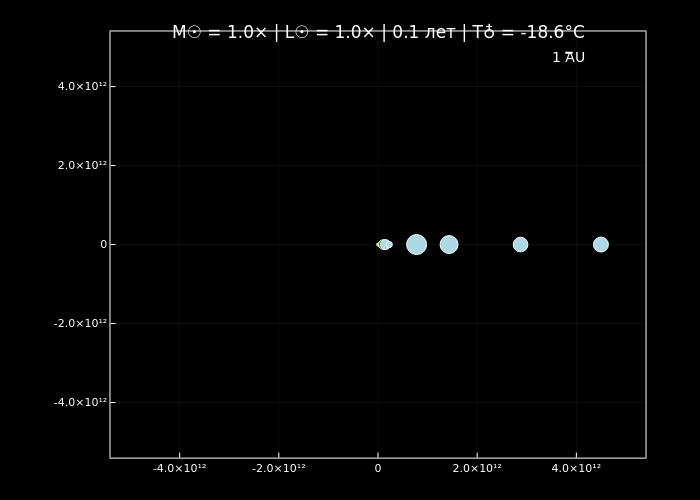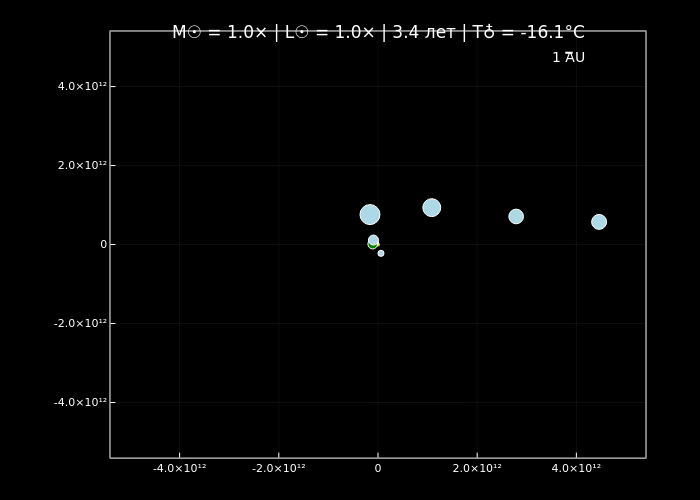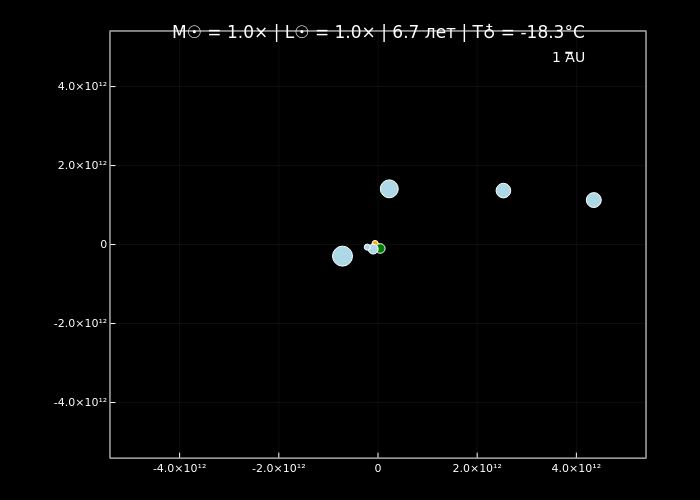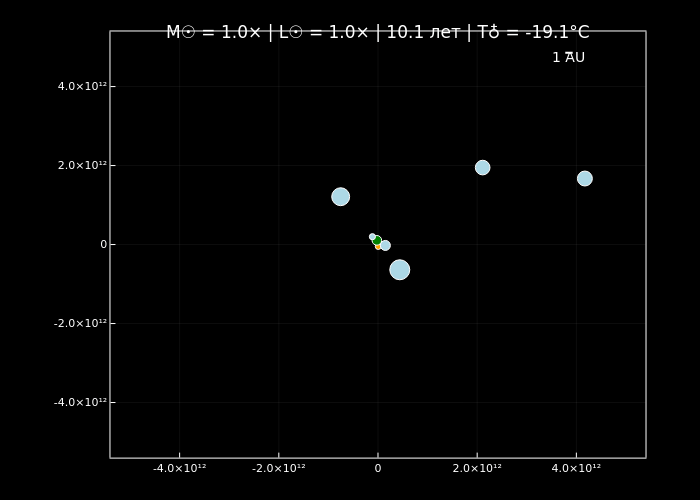
Анимация сохранена: normal_sun.gif

simulate_solar_system(10.0, years=5, step_days=2, filename="massive_sun_10x.gif");

Симуляция: M☉ = 10.0×, 5 лет, шаг 2 дней
Анимация сохранена: massive_sun_10x.gif

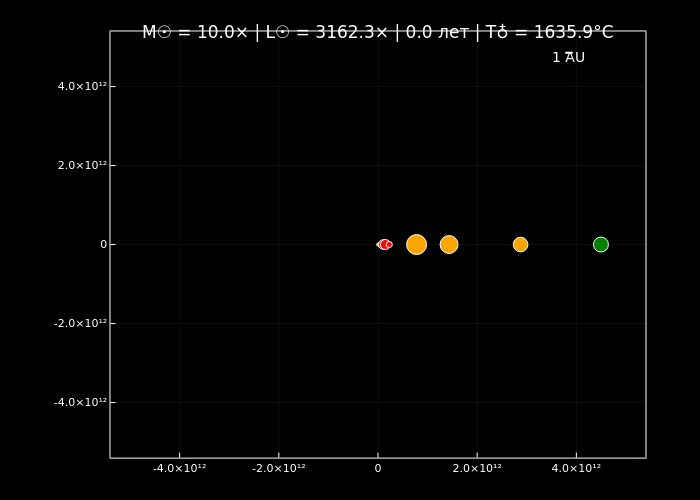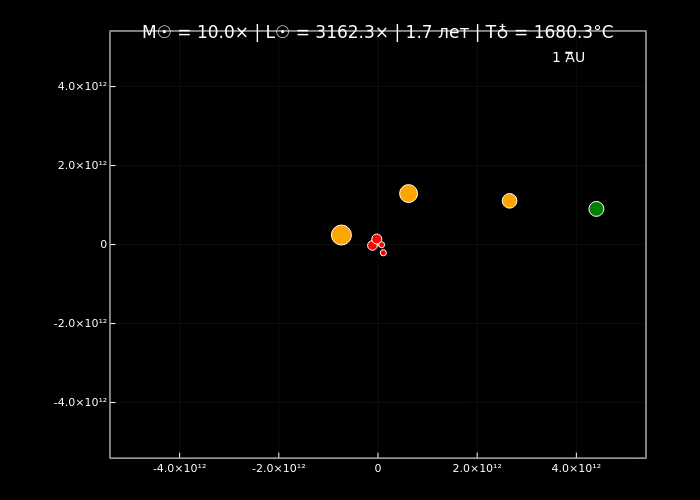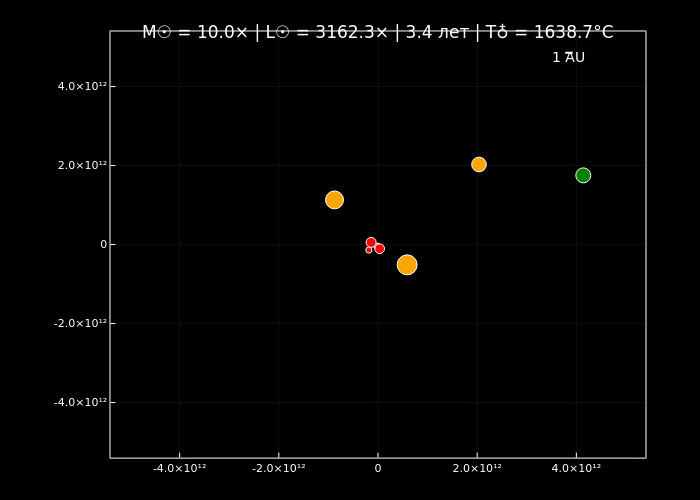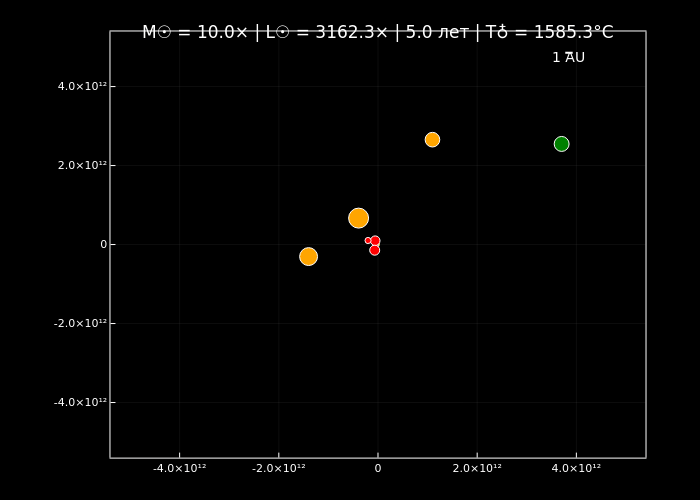
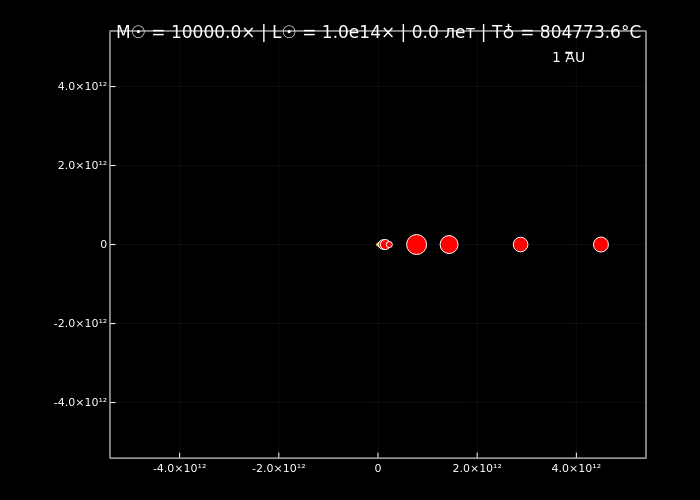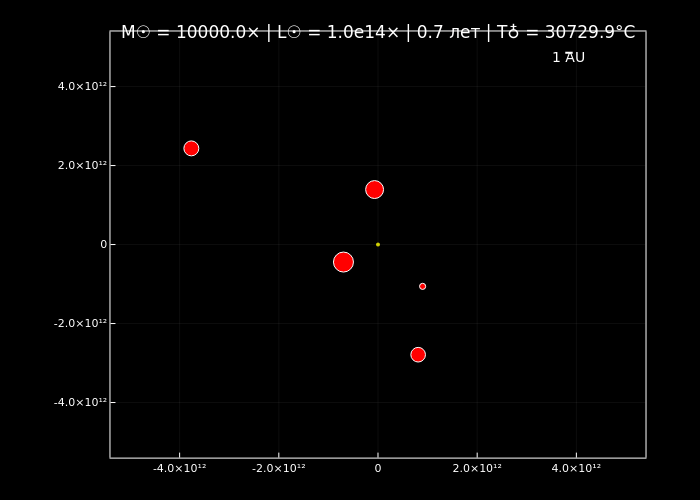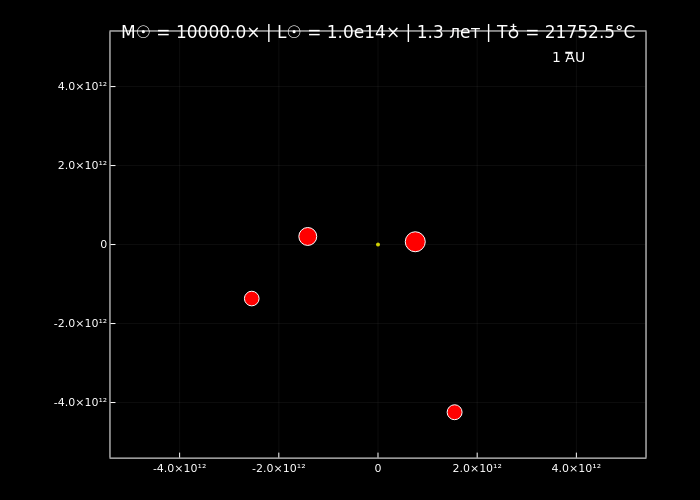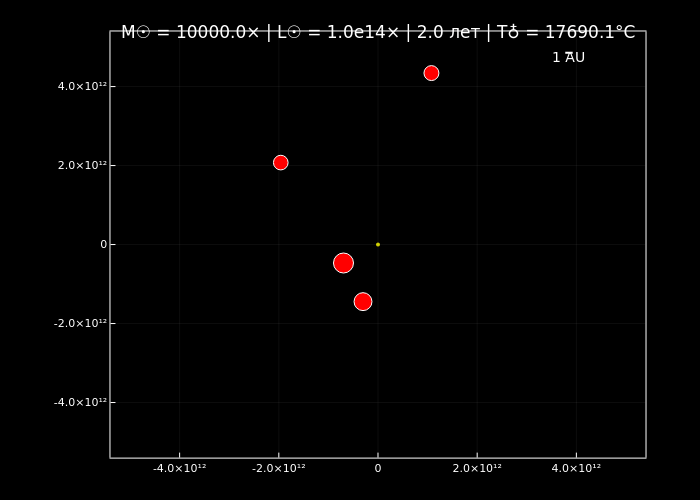
simulate_solar_system(10000.0, years=2, step_days=1, filename="extreme_sun_10000x.gif");

Симуляция: M☉ = 10000.0×, 2 лет, шаг 1 дней
Анимация сохранена: extreme_sun_10000x.gif

Вывод

Выполненные тесты демонстрируют два ключевых физических следствия изменения массы Солнца.

Температурный анализ (create_temperature_stats()) наглядно показывает, что зависимость светимости от массы приводит к экстремальному росту температуры планет. Даже при 10-кратной массе Солнца температуры на внутренних планетах превышают точку кипения воды, а при увеличении массы до 10⁶–10⁷ солнечных все планеты раскаляются выше 1000°C, что иллюстрирует фундаментальную связь между структурой звезды и климатическими условиями в системе.

Симуляции орбитальной динамики подтверждают, что увеличение массы Солнца ускоряет орбитальное движение планет (по закону Кеплера) и меняет стабильность их траекторий благодаря доминированию гравитации центрального тела. Анимации визуализируют эти эффекты: при нормальной массе (normal_sun.gif) планеты демонстрируют классические кеплеровские орбиты, а с её ростом (massive_sun_10x.gif, extreme_sun_10000x.gif) их движение становится быстрее, а цвет меняется от холодных оттенков к раскалённо-красным.

Моделирование Солнечной системы

Моделирование Солнечной системы.

Вывод

Тип

Краткое описание

Связанные материалы

Теги

Категории

Языки

Форматы

Уровень

Статус

Опубликовано

Обновлено

Источник