Нахождение кратчайших путей в графе по алгоритму Дийкстры
Нахождение кратчайших путей в графе, используя алгоритм Дийкстры
Создание графа на примере транспортной сети из матрицы смежности, считанной с Excel. Нахождение кратчайших путей в "прыжках" и расстояниях с помомощью алгоритма Дийкстры. Запись результат в Excel.
Описание задачи
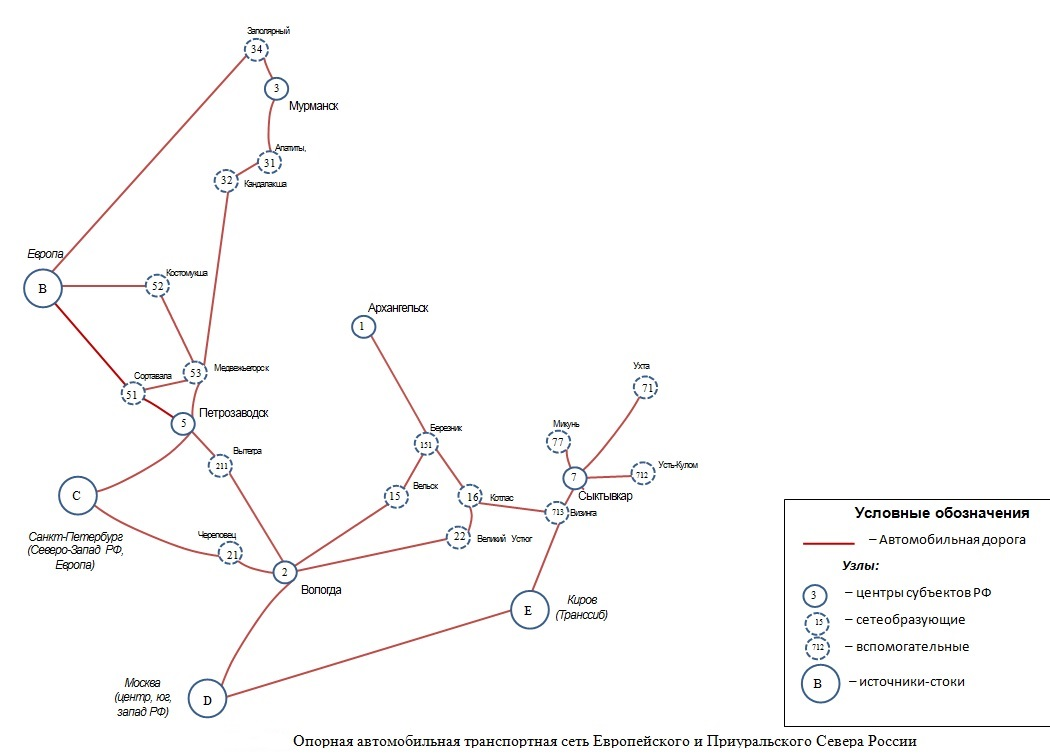
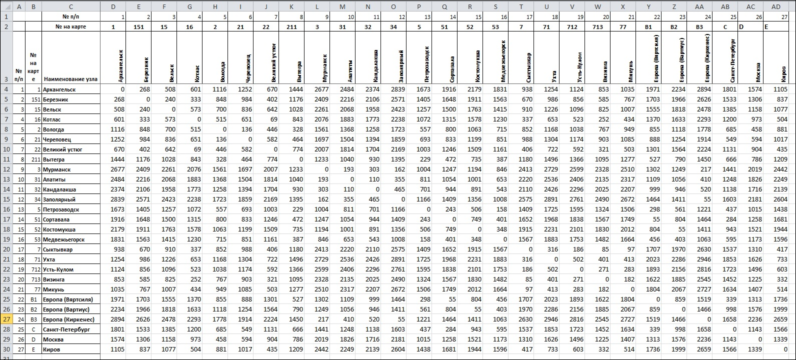
Имеется автомобильная транспортная сеть (см. рисунок). имеется Excel-файл, в котором занесена информация о данной транспортной сети в виде матрицы смежности и таблицы с расстояниями между узлами сети.
Транспортная сеть – ненаправленный граф, т.е. по ребру можно перемещаться в прямом и обратном напрявлениях. Помимо того что графы могут быть направленными или ненаправленными, они могут быть также взвешенными или невзвешенными. Взвешенный граф — это такой граф, у которого с каждым из ребер связано некое сопоставимое значение, обычно числовое. В потенциальной транспортной сети вес ребер – это расстояния между узлами.
Задача заключается в поиске оптимальных путей между узлами (вершинами) в «прыжках» на невзвешенном графе и в расстояниях на взвешенном графе. За чем это надо?
Если бы вид транспорта на данной транспортной сети был бы настолько быстрый по скорости, то для оптимизации времени в пути между узлами, вероятно, потребуется считать количество ребер, так как расстояние между ними имеет гораздо меньшее значение, чем то, сколько прыжков потребуется (сколько узлов придется посетить), чтобы добраться от узла до другого. Каждая станция может означать задержку, поэтому, как и при полетах на самолете, чем меньше остановок, тем лучше.
img = load( "$(@__DIR__)/pics/ОТС_без карты.jpg" )
Алгоритм Дийкстры (англ. Dijkstra’s algorithm) —
алгоритм на графах, изобретённый нидерландским учёным Эдсгером Дейкстрой в 1959 году. Находит кратчайшие пути от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса. Алгоритм широко применяется в программировании и технологиях, например, его используют протоколы маршрутизации OSPF и IS-IS.
using Pkg
Pkg.add("GraphRecipes")
Pkg.add("SimpleWeightedGraphs")
Pkg.add("GraphPlot")
using Graphs, GraphRecipes, GraphPlot, SimpleWeightedGraphs
using XLSX, Plots
Поиск кратчайшего пути в "прыжках" на невзвешенном графе.
Считаем матрицу смежности с Excel, построим невзвешанный граф
room = Matrix(Int64.(XLSX.readdata("Data.xlsx", "Исходник", "D4:AD30"))) # Считывает данные с Excel-файла в матрицу {Int64},
# потому что SimpleGraph c {Any} у меня не работает.
graph_room = SimpleGraph(room) #Постройте SimpleDiGraph{T} из матрицы смежности adjm. Если adjm[i][j] != 0, то вставляется ребро (i, j).
#adjm должна быть квадратной матрицей. Тип элемента T может быть опущен.
# SimpleGraph - не ориентированный граф, SimpleDiGraph - ориентированный граф.
# определяем кол-во вершин и ребер графа
vershiny = nv(graph_room) # Количество вершин
rebra = ne(graph_room) # Количество ребер
println( "Количество вершин = ", vershiny)
println("Количество ребер = ", rebra )
# Отрисовка графа условно
graphplot(graph_room,
markersize = 0.2,
names = 1:vershiny,
fontsize = 10,
linecolor = :darkgrey
)
#graphplot(graph_room, names=1:nv(graph_room))
Например, найдем кратчайший путь в "прыжках" от любой вершины до другой вершины с помощью алгоритма Дийкстра. Перечислим путь.
path_1_24=enumerate_paths(dijkstra_shortest_paths(graph_room, 1), 24) # кратчайший путь от вершины 1 до вершины 24
path_27_1 = enumerate_paths(dijkstra_shortest_paths(graph_room, 27), 1) # кратчайший путь от вершины 27 до вершины 1
# Найдем за сколько "прыжков" мы доберемся от вершины 27 до вершины 1.
count_jumps_27_1 = length(path_27_1)-1 # количество "прыжков"
# найти кратчайший путь от вершины 1 до всех вершин с помощью алгоритма Дийкстра.Перечислить пути.
path_1_all = enumerate_paths(dijkstra_shortest_paths(graph_room, 1))
Найдем количество "прыжков" от каждой вершины ко всем вершинам по кратчайшим путям
mass = [enumerate_paths(dijkstra_shortest_paths(graph_room, x)) for x in 1:vershiny] # массив из всех перечисленных путей от каждой вершине ко всем вершинам
count_jumps = zeros(vershiny,vershiny)
for i in 1:vershiny
for j in 1:vershiny
count_jumps[i,j] = length(mass[i][j])
if count_jumps[i,j] > 0
count_jumps[i,j] -= 1
end
end
end
count_jumps
Запишем результат в файл Excel
#=
Записывыает только результат в имеющийся файл result.xlsx, заранее подготовленный с листом "Количество_прыжков",
где уже внесена таблица (шапочка). Файл должен быть закрыт в это время. Данные переносяться и сохраняются.
=#
XLSX.openxlsx("result.xlsx", mode="rw") do xf # Редактирование существующего файла: режим "rw"
sheet = xf["Количество_прыжков"] # Обратиться к листу "Количество_прыжков"
sheet["D4:AD30"] = count_jumps # записать в ячейки D4:AD30 матрицу результатов
end;
Поиск кратчайшего пути по расстояниям на взвешенном графе.
В этом примере воспользуемся функциями библиотеки SimpleWeightedGraphs.jl чтобы создать граф и найти на нем кратчайшие маршруты от всех вершин ко всем вершинам.
Взвешенный граф - граф, в котором у каждого ребра и/или каждой вершины есть “вес” - некоторое число, которое может обозначать длину пути, его стоимость и т. п.
SimpleWeightedGraphs.jl- этот пакет определяет два новых типа графиков: SimpleWeightedGraph и SimpleWeightedDiGraph. Ознакомьтесь с руководством , чтобы узнать, что вы можете с ними сделать.
Также обратитесь к пакету Graphs.jl для получения более сложных алгоритмов.
using DataFrames
#graph_room_2 = SimpleWeightedGraph(room) # SimpleWeightedGraph(adjmx) создает граф из матрицы смежности adjm.
# Считывает данные с Excel-файла в матрицу, оборачиваем матрицу в таблицу с шапочкой для наглядности.
distance = DataFrame(XLSX.readdata("Data.xlsx", "Исходные_Авто_км", "E2:G32"), ["УзелНачала", "УзелКонец", "Расстояние"])
# Число узлов
n = max(maximum(distance[:,:УзелНачала]), maximum(distance[:,:УзелКонец]))
# Число ребер
r = nrow(distance) # Число ребер (дуг) r = количеству строк в таблице
# size(isdan,1) - размер строк, то же самое будет: nrow(isdan)
Строим взвешанный неориентированный граф
# Строим граф
#= SimpleWeightedGraphs.jl предоставляет структуру для (не) ориентированных графов
с возможностью задания весов на ребрах. Если вам нужны веса ребер и не требуется большого количества модификаций графика,
используйте SimpleWeightedGraphs.jl =#
graph_distance=SimpleWeightedGraph(n) # используйте "Простой взвешенный Орграф" для неориентированных графов.
#добавляем ребра с их расстояниями (весами)
for i=1:r
add_edge!(graph_distance, distance[i,:УзелНачала], distance[i,:УзелКонец], distance[i,:Расстояние])
end
# Если вместо расстояния поставить 1, то получим невзвешанный, неориентированный граф
#Для примера, как вывести крайтчайшие расстояния
bb = dijkstra_shortest_paths(graph_distance, 1) # для примера, найдем крайтчайший путь от вершины 1 до всех вершин с помощью алгоритма Дийкстра
bb.dists # вывести крайтчайший расстояния от вершины 1 до всех вершин
Найдем кратчайшие расстояния от каждой вершины ко всем вершинам с помощью алгоритма Дийкстра
# Найдем кратчайшие расстояния от каждой вершины ко всем вершинам с помощью алгоритма Дийкстра
masskm = [dijkstra_shortest_paths(graph_distance, y).dists for y in 1:n]
distance_count = zeros(n,n)
for i in 1:n
for j in 1:n
distance_count[i,j] = masskm[i][j]
end
end
distance_count
Запишем результат в файл Excel
#=
Записывыает только результат в имеющийся файл result.xlsx, заранее подготовленный с листом "Количество_прыжков",
где уже внесена таблица (шапочка). Файл должен быть закрыт в это время! Данные переносяться и сохраняются.
=#
XLSX.openxlsx("result.xlsx", mode="rw") do xf # Редактирование существующего файла: режим "rw"
sheet = xf["Кратчайшие_расстояния"] # Обратиться к листу "Кратчайшие_расстояния"
sheet["D4:AD30"] = distance_count # записать в ячейки D4:AD30 матрицу результатов
end;
# В результате получаем ответ в excel-файле
img = load( "$(@__DIR__)/pics/Result_Dijksta.jpg" )
Сравним, есть ли разница между кратчайшими путями в "прыжках" и в"прыжках" по расстоянию
прыжки_1_5 = enumerate_paths(dijkstra_shortest_paths(graph_room, 1), 5) # "прыжки" по узлам в невзвешанном графе
расстояние_1_5 = enumerate_paths(dijkstra_shortest_paths(graph_distance, 1), 5) # "прыжки"по узлам в взвешанном графе
прыжки_1_5 == расстояние_1_5 # сравниваем "прыжки" по узлам
Заключение
Разница в количествах "прыжков" посещаемых вершин есть.Когда это может пригодиться?
Если бы вид транспорта на данной транспортной сети был бы настолько быстрый по скорости,
то для оптимизации времени в пути между узлами, вероятно, потребуется считать количество ребер,
так как расстояние между ними имеет гораздо меньшее значение, чем то, сколько прыжков потребуется (сколько узлов
придется посетить), чтобы добраться от одного узла до другого. Каждая станция может означать задержку,
поэтому, как и при полетах на самолете, чем меньше остановок, тем лучше
=#