Определение ЛАФЧХ линейной системы с помощью PRBS
Определение частотной характеристики линейной системы с помощью блока генератора сигнала псевдослучайной двоичной последовательности
Введение
В данном примере мы рассмотрим процесс определения частотной характеристики линейной системы в модели с использованием блока генератора сигнала псевдослучайной двоичной последовательности (PRBS Signal Generator). Также сравним полученные частотные характеристики с частотными характеристиками аналогичного динамического звена.
Получение частотного отклика с помощью сигнала псевдослучайной двоичной последовательности
Псевдослучайная двоичная последовательность — это периодический сигнал, который может принимать только два определенных значения.
С помощью данного сигнала можно определять частотный отклик исследуемой системы. Для получения частного отклика в модели служит блок Генератор сигнала псевдослучайной двоичной последовательности.
Суть алгоритма определения частотного отклика аналогичен методу гармонического анализа и заключается в следующем. Тестовый сигнал подается на вход системы и измеряется ее выход.
Для корректного определения частотного отклика необходимы также стартстопный и сам тестовый сигналы.
Сигнал псевдослучайной двоичной последовательности имеет преимущество перед гармоническим сигналом: эксперимент по определению частотного отклика короче без снижения качества результатов анализа.
Описание модели
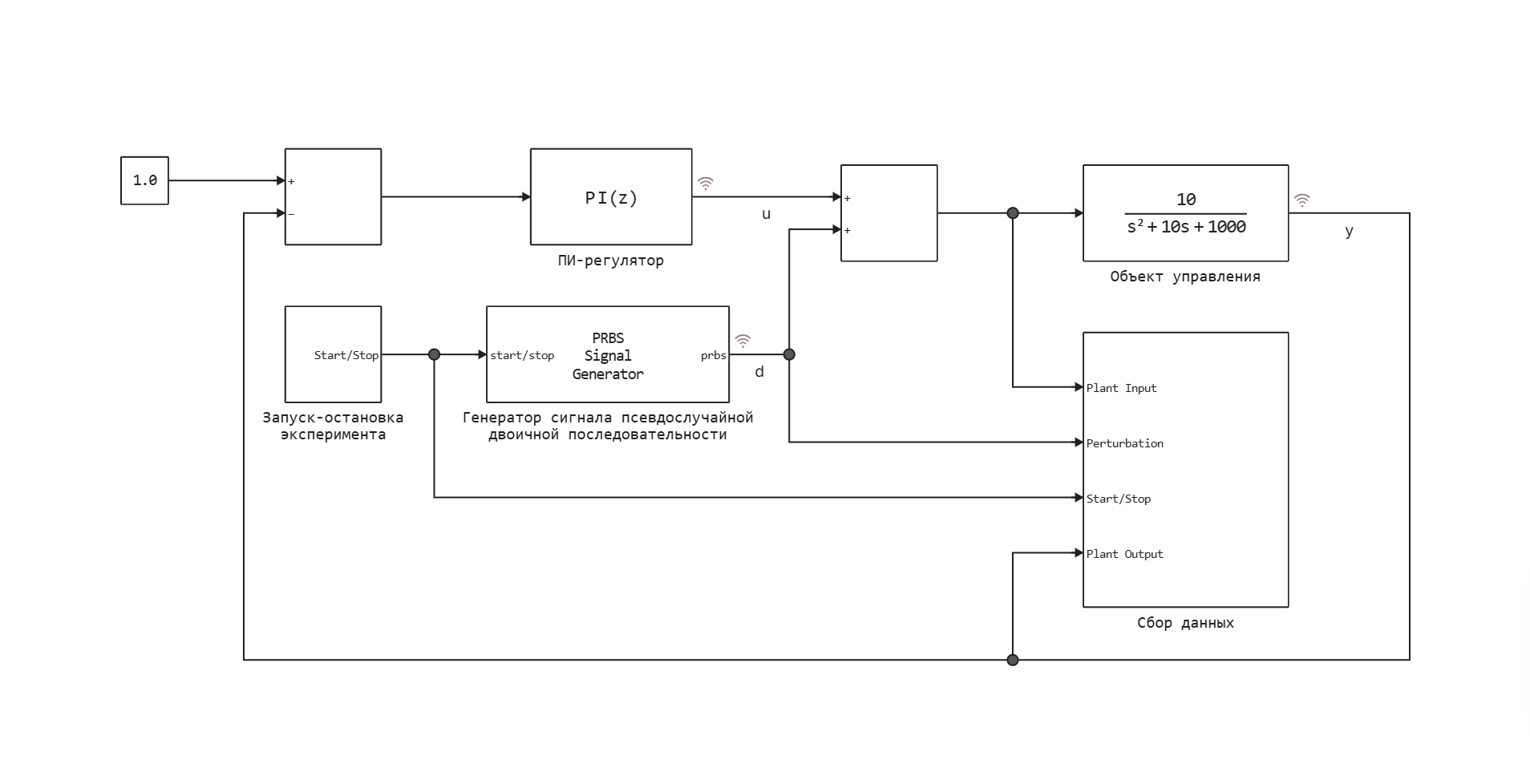
Модель представляет собой замкнутую систему управления и включает объект управления в виде передаточной функции второго порядка, дискретный ПИ-регулятор и блоки для определения частотного отклика системы: Генератор сигнала псевдослучайной двоичной последовательности, Запуск-остановка эксперимента и Сбор данных.
В блоке Запуск-остановка эксперимента формируется стартстопный сигнал. Блок Сбор данных служит для предобработки и экспорта в Рабочую область сигналов модели, требуемых для вычисления частотного отклика системы. Собранные сигналы сохраняются в переменную PRBSSigGenData.
Запуск модели
Загружаем нужные библиотеки
using EngeeDSP
using Plots
try
using ControlSystemsBase
catch
Pkg.add("ControlSystemsBase")
using ControlSystemsBase
end
try
using DSP
catch
Pkg.add("DSP")
using DSP
end
Объявляем переменные
# Период дискретизации алгоритма
Ts = 0.005;
# Массив частот, на которых будет собираться частотный отклик, — от 1 до 100 рад/с
w = [1.0; 1.274274985703134; 1.623776739188722; 2.069138081114790; 2.636650898730358;
3.359818286283782; 4.281332398719393; 5.455594781168519; 6.951927961775605; 8.858667904100825;
11.288378916846890; 14.384498882876629; 18.329807108324356; 23.357214690901223; 29.763514416313178;
37.926901907322502; 48.329302385717526; 61.584821106602639; 78.475997035146108; 100.0];
Запускаем симуляцию
modelName = "prbs_signal_gen";
if modelName ∉ getfield.(engee.get_all_models(), :name)
engee.load("$(@__DIR__)/$(modelName).engee");
end
engee.run(modelName);
Обработка результатов моделирования
Записываем данные симуляции в переменные
model_data = collect(PRBSSigGenData);
t = model_data[:,1];
data = model_data[:,2]
nd = size(data, 1)
nw = length(w)
ready = zeros(nd)
perturbation = zeros(nd)
input = zeros(nd)
output = zeros(nd)
for i = 1:nd
ready[i] = data[i][1]
perturbation[i] = data[i][2]
input[i] = data[i][3]
output[i] = data[i][4]
end
Обрабатываем сигналы перед вычислением частотного отклика системы
ts = t[2] - t[1]
dupidx = findall(diff(t) .< ts/2)
deleteat!(ready, dupidx)
deleteat!(perturbation, dupidx)
deleteat!(input, dupidx)
idx = findall(ready .== 1.)
d = perturbation[idx]
u = input[idx]
y = output[idx]
nfft = sum(idx .> 0.)
if !iszero(rem(nfft, 2))
freq = (2*pi/ts) .* collect(range(0., 1., nfft + 1))
lastel = Int64((nfft + 1) / 2)
freq = freq[1:lastel]
else
freq = (pi/ts) .* collect(range(0., 1., Int64(nfft/2) + 1))
end
pd = 2*pi / (nfft - 1)
filterwindow = [0.5 .* ones(nfft-1) .- 0.5 .* cos.(pd .* collect(0:nfft-2)); 0.]
fd = EngeeDSP.fft(d .* filterwindow);
fu = EngeeDSP.fft(u .* filterwindow);
fy = EngeeDSP.fft(y .* filterwindow);
d2u = fu ./ fd;
d2y = fy ./ fd;
u2y = d2y ./ d2u;
Построение частотной характеристики
Получаем частотный отклик системы
# Подключаем файл со служебной функцией
include("$(@__DIR__)/interpfreqresp.jl")
plant_response = interpfreqresp(freq, u2y[1:length(freq)], w);
Вычисляем логарифмическую амплитудно-фазовую частотную характеристику (ЛАФЧХ) системы по частотному отклику
magnitude_estimated = 20 * log10.(abs.(plant_response));
phase_estimated = rad2deg.(DSP.unwrap((atan.(imag.(plant_response), real.(plant_response)))));
Вычисляем ЛАФЧХ передаточной функции системы. Перед этим дискретизируем передаточную функцию с периодом квантования, равным периоду дискретизации алгоритма
W = c2d(tf([10.0], [1.0; 10.0; 1000.0]), ts)
magnitude_ideal, phase_ideal, w_ideal = bode(W);
magnitude_ideal = 20 * log10.(reshape(magnitude_ideal, size(magnitude_ideal, 3),))
phase_ideal = reshape(phase_ideal, size(phase_ideal, 3),);
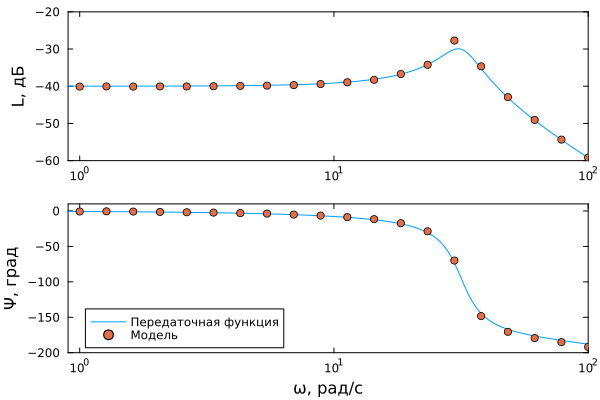
Строим ЛАФЧХ
gr()
p1 = plot(w_ideal, magnitude_ideal, ylims = (-60,-20), ylabel = "L, дБ", legend = :none)
plot!(w, magnitude_estimated, linealpha = 0.0, markershape = :circle, markersize = 4)
p2 = plot(w_ideal, phase_ideal, ylims = (-200,10), xlabel = "ω, рад/с", ylabel = "Ψ, град", label = "Передаточная функция", legend = :bottomleft)
plot!(w, phase_estimated, linealpha = 0.0, markershape = :circle, markersize = 4, label = "Модель")
plot(p1, p2, layout = (2,1), grid = false, framestyle = :box, xscale=:log10, xlims = (0.9,100))
Видно, что ЛАФЧХ передаточной функции и ЛАФЧХ, полученная по частотному отклику из модели, практически совпадают.
Заключение
В данном примере мы рассмотрели, как построить ЛАФЧХ по частотному отклику системы в модели, полученного с помощью тестового сигнала псевдослучайной двоичной последовательности. Также убедились в том, что построенная таким образом ЛАФЧХ практически совпадает с ЛАФЧХ передаточной функции модели.