Определение ЛАФЧХ повышающего преобразователя с помощью PRBS
Определение частотной характеристики повышающего преобразователя с помощью блока генератора сигнала псевдослучайной двоичной последовательности
Введение
В данном примере мы рассмотрим процесс определения частотной характеристики передаточной функции выходного сопротивления повышающего преобразователя в модели с использованием блока генератора сигнала псевдослучайной двоичной последовательности (PRBS Signal Generator). Также сравним полученные частотные характеристики с частотными характеристиками линейной модели устройства.
Получение частотного отклика с помощью сигнала псевдослучайной двоичной последовательности
Псевдослучайная двоичная последовательность — это периодический сигнал, который может принимать только два определенных значения.
С помощью данного сигнала можно определять частотный отклик исследуемой системы. Для получения частного отклика в модели служит блок Генератор сигнала псевдослучайной двоичной последовательности.
Суть алгоритма определения частотного отклика аналогичен методу гармонического анализа и заключается в следующем. Тестовый сигнал подается на вход системы и измеряется ее выход.
Для корректного определения частотного отклика необходимы также стартстопный и сам тестовый сигналы.
Сигнал псевдослучайной двоичной последовательности имеет преимущество перед гармоническим сигналом: эксперимент по определению частотного отклика короче без снижения качества результатов анализа.
Описание модели
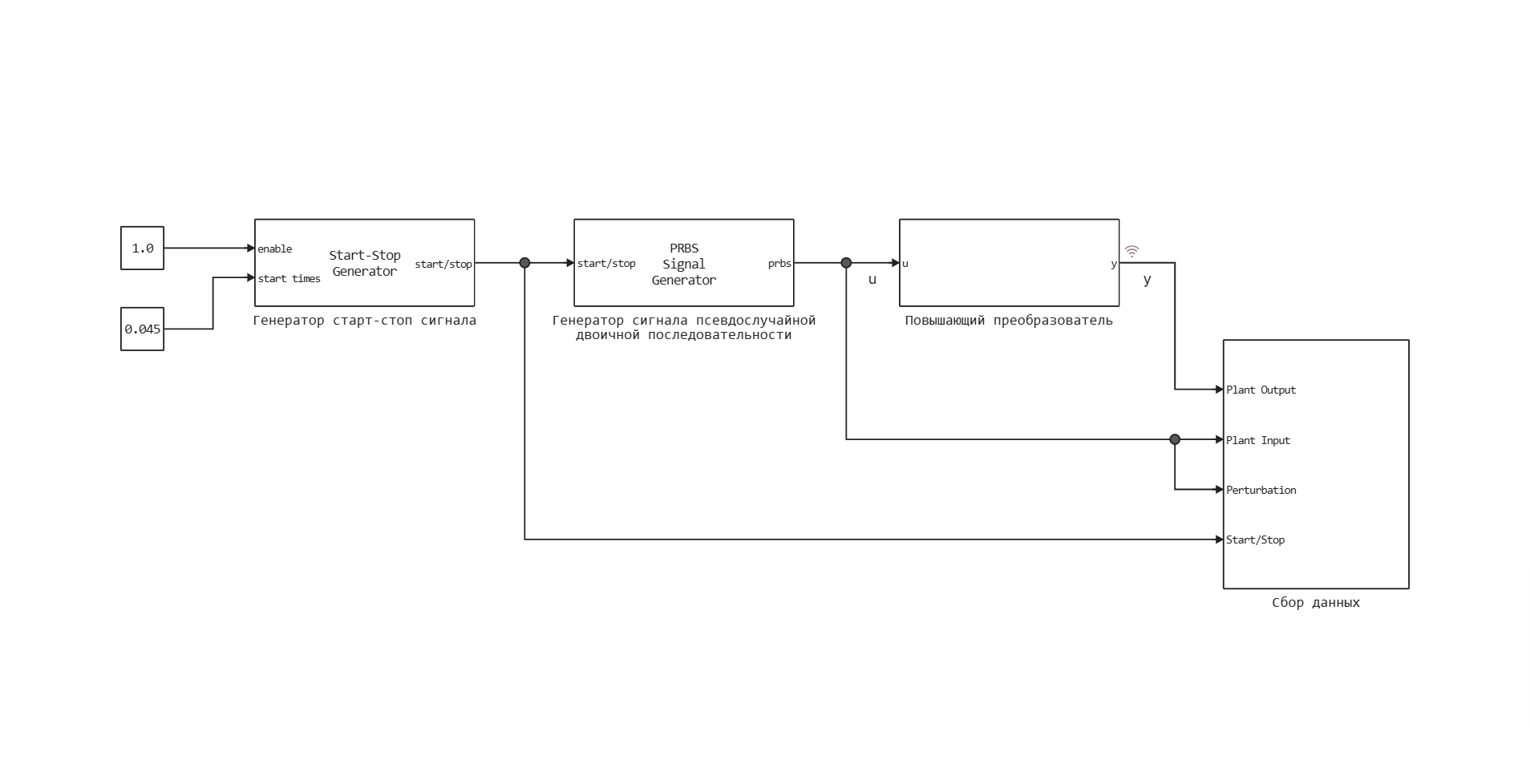
Модель состоит из исследуемой системы — повышающего преобразователя (Boost Converter) — и блоков, служащих для определения частотного отклика системы: Генератор сигнала псевдослучайной двоичной последовательности, Генератор старт-стоп сигнала и Сбор данных.
Блок Генератор старт-стоп сигнала служит для формирования стартстопного сигнала, который управляет запуском и длительностью эксперимента по определению частотного отклика. Блок Сбор данных служит для предобработки и экспорта в Рабочую область сигналов модели, требуемых для вычисления частотного отклика системы. Собранные сигналы сохраняются в переменную PRBSSigGenData.
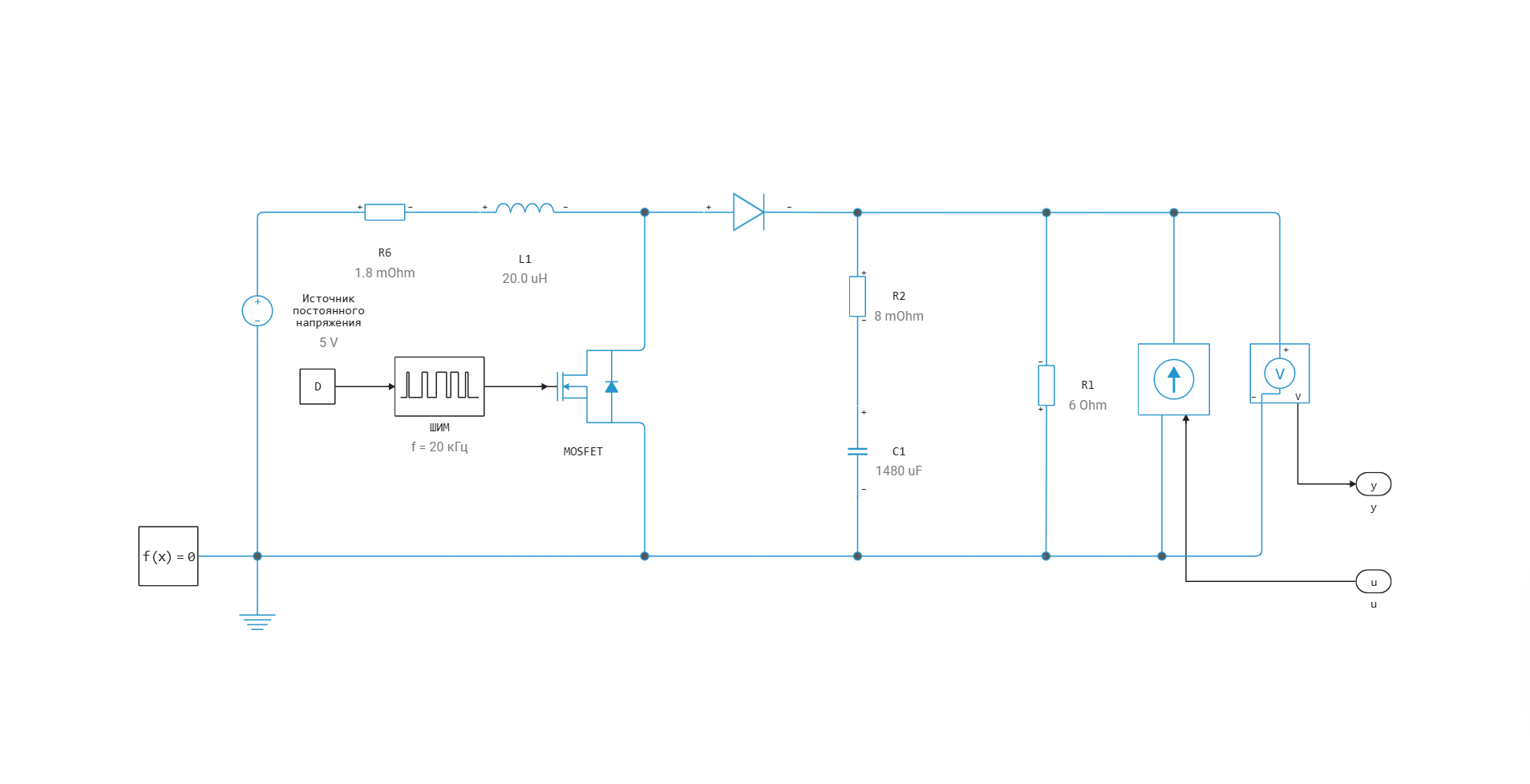
Повышающий преобразователь повышает входное напряжение 5В до 18В. Он собран на базе МОП-транзистора. Частота ШИМ 20 кГц.
Для определения частотного отклика передаточной функции выходного сопротивления подаем тестовый сигнал тока нагрузки (сигнал u) и снимаем выходное напряжение преобразователя (сигнал y).
Запуск модели
Загружаем нужные библиотеки
using EngeeDSP
using Plots
try
using ControlSystemsBase
catch
Pkg.add("ControlSystemsBase")
using ControlSystemsBase
end
try
using DSP
catch
Pkg.add("DSP")
using DSP
end
Объявляем переменные
L = 20e-6; # Индуктивность катушки, Гн
C = 1480e-6; # Емкость выходного конденсатора, Ф
R = 6; # Сопротивление нагрузки, Ом
rC = 8e-3; # Эквивалентное последовательное сопротивление конденсатора, Ом
rL = 1.8e-3; # Эквивалентное последовательное сопротивление катушки, Ом
D = 0.734785; # Коэффициент заполнения
d = 1 - D;
# Передаточная функция преобразователя [1, п. 11.7]
Zout = tf(R*[C*rC*L; L+C*rC*(rL+R*D*rC*d/(R+rC)); rL+R*D*rC*d/(R+rC)],
[L*C*(R+rC); L+C*rL*(R+rC)+C*R*rC-R*D*C*rC; R+rL-R*D-R^2*D*d/(R+rC)]);
# Период ШИМ и дискретизации алгоритма
Ts = 5e-5
# Массив частот, на которых будет собираться частотный отклик, — от 200 рад/с and 60000 рад/с
w = [2e+02; 2.700255121992927e+02; 3.645688861924518e+02; 4.922145011302122e+02; 6.645523638980243e+02;
8.972304622240737e+02; 1.211375575614318e+03; 1.635511551354846e+03; 2.208149221812260e+03; 2.981283123161623e+03;
4.025112511714125e+03; 5.434415338176934e+03; 7.337153925974601e+03; 9.906093734731705e+03; 1.337449017307568e+04;
1.805726779694581e+04; 2.437961492895045e+04; 3.291559004205681e+04; 4.444024530224159e+04; 6e+04];
Запускаем симуляцию
modelName = "prbs_boost_converter";
if modelName ∉ getfield.(engee.get_all_models(), :name)
engee.load("$(@__DIR__)/$(modelName).engee");
end
engee.run(modelName);
Обработка результатов моделирования
Записываем данные симуляции в переменные
model_data = collect(PRBSSigGenData);
t = model_data[:,1];
data = model_data[:,2]
nd = size(data, 1)
nw = length(w)
ready = zeros(nd)
perturbation = zeros(nd)
input = zeros(nd)
output = zeros(nd)
for i = 1:nd
ready[i] = data[i][1]
perturbation[i] = data[i][2]
input[i] = data[i][3]
output[i] = data[i][4]
end
Обрабатываем сигналы перед вычислением частотного отклика системы
ts = t[2] - t[1]
dupidx = findall(diff(t) .< ts/2)
deleteat!(ready, dupidx)
deleteat!(perturbation, dupidx)
deleteat!(input, dupidx)
idx = findall(ready .== 1.)
d = perturbation[idx]
u = input[idx]
y = output[idx]
nfft = sum(idx .> 0.)
if !iszero(rem(nfft, 2))
freq = (2*pi/ts) .* collect(range(0., 1., nfft + 1))
lastel = Int64((nfft + 1) / 2)
freq = freq[1:lastel]
else
freq = (pi/ts) .* collect(range(0., 1., Int64(nfft/2) + 1))
end
pd = 2*pi / (nfft - 1)
filterwindow = [0.5 .* ones(nfft-1) .- 0.5 .* cos.(pd .* collect(0:nfft-2)); 0.]
fd = EngeeDSP.fft(d .* filterwindow);
fu = EngeeDSP.fft(u .* filterwindow);
fy = EngeeDSP.fft(y .* filterwindow);
d2u = fu ./ fd;
d2y = fy ./ fd;
u2y = d2y ./ d2u;
Построение частотной характеристики
Получаем частотный отклик системы
# Подключаем файл со служебной функцией
include("$(@__DIR__)/interpfreqresp.jl")
plant_response = interpfreqresp(freq, u2y[1:length(freq)], w);
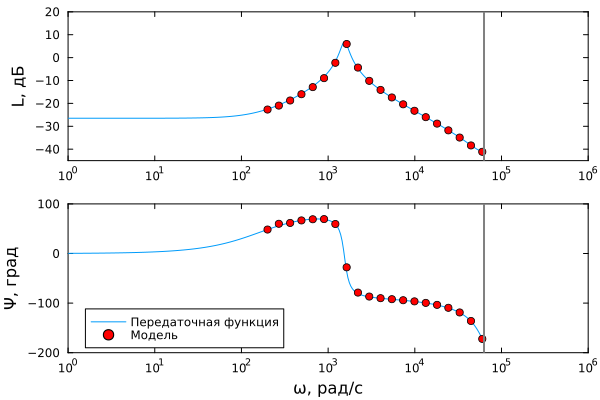
Вычисляем логарифмическую амплитудно-фазовую частотную характеристику (ЛАФЧХ) системы по частотному отклику
magnitude_estimated = 20 * log10.(abs.(plant_response));
phase_estimated = rad2deg.(DSP.unwrap((atan.(imag.(plant_response), real.(plant_response)))));
Вычисляем ЛАФЧХ передаточной функции системы. Перед этим дискретизируем передаточную функцию с периодом квантования, равным периоду дискретизации алгоритма
W = c2d(Zout, Ts)
magnitude_ideal, phase_ideal, w_ideal = bode(W);
magnitude_ideal = 20 * log10.(reshape(magnitude_ideal, size(magnitude_ideal, 3),))
phase_ideal = reshape(phase_ideal, size(phase_ideal, 3),);
Строим ЛАФЧХ
gr()
p1 = plot(w_ideal, magnitude_ideal, ylims = (-45,20), ylabel = "L, дБ", legend = :none)
scatter!(w, magnitude_estimated, mc = :red, ms = 4)
plot!([pi/Ts; pi/Ts],[-45; 20], lc = :gray, lw = 2)
p2 = plot(w_ideal, phase_ideal, ylims = (-200,100), xlabel = "ω, рад/с", ylabel = "Ψ, град", label = "Передаточная функция", legend = :bottomleft)
scatter!(w, phase_estimated, mc = :red, ms = 4, label = "Модель")
plot!([pi/Ts; pi/Ts],[-200; 100], lc = :gray, lw = 2, label = "")
plot(p1, p2, layout = (2,1), grid = false, framestyle = :box, xscale=:log10, xlims = (1,1e6))
Видно, что ЛАФЧХ передаточной функции и ЛАФЧХ, полученная по частотному отклику из модели, практически совпадают.
Заключение
В данном примере мы рассмотрели, как построить ЛАФЧХ повышающего преобразователя по частотному отклику системы в модели, полученного с помощью тестового сигнала псевдослучайной двоичной последовательности. Также убедились в том, что построенная таким образом ЛАФЧХ практически совпадает с ЛАФЧХ линеаризованной передаточной функции устройства.
Использованные источники
- Pulse-Width Modulated DC–DC Power Converters. Second Edition. Marian K. Kazimierczuk. 2016