Оптимизация СМО
Оптимизация распределения потоков в системах массового обслуживания
В современном цифровом мире — от глобальных сетей передачи данных до логистических цепочек и систем обработки транзакций — мы постоянно сталкиваемся с необходимостью эффективного управления потоками. Как обеспечить бесперебойную работу интернет-соединений при пиковых нагрузках? Как оптимизировать маршруты доставки товаров в мегаполисе? Как спроектировать call-центр, чтобы клиенты не ждали ответа? Ответы на эти вопросы лежат в области теории массового обслуживания — математической дисциплины, изучающей системы, где заявки (пакеты данных, клиенты, транспортные средства) поступают на обслуживание, образуя очереди.
Система массового обслуживания (СМО) представляет собой математическую модель, состоящую из обслуживающих устройств (каналов, серверов, узлов) и потока заявок, которые эти устройства обрабатывают. Особый интерес представляет система M/M/1 — фундаментальная модель, где входящий поток заявок имеет пуассоновский характер (случайные, независимые события с постоянной средней интенсивностью), а время обслуживания подчиняется экспоненциальному распределению (характеризующемуся свойством "отсутствия памяти"). Эта простая, но глубокая модель раскрывает парадоксальную природу очередей: при приближении нагрузки к 100% длина очереди растёт гиперболически, а не линейно, делая оптимизацию не просто желательной, а критически необходимой.
Сетевые СМО — следующий уровень сложности, где множество обслуживающих узлов соединены в сеть. Такая система естественно описывается направленным графом, где узлы представляют точки обработки, а ветви — каналы связи с ограниченной пропускной способностью. Для математического представления структуры сети используются матрица смежности (описывающая наличие связей между узлами) и матрица инцидентности (фиксирующая направления этих связей). Именно эти математические объекты становятся строительными блоками для постановки задачи оптимизации.
Но как найти оптимальное распределение потоков в сложной сети? Как направить информационные потоки или транспортные средства так, чтобы минимизировать среднее время ожидания в системе, не допуская при этом перегрузки отдельных каналов? Эта задача решается с помощью нелинейной оптимизации, где целевая функция — сумма средних чисел заявок во всех каналах (выведенная из формулы для M/M/1), а ограничения включают баланс потоков в узлах и физические ограничения пропускных способностей.
В данной работе мы представляем полный цикл анализа и оптимизации сетевой СМО — от теоретических основ до практической реализации в среде Engee. Вы увидите, как:
-
Преобразовать реальные данные о пропускных способностях и потоках в математические модели;
-
Визуализировать сложные сетевые структуры с помощью графов;
-
Сформулировать задачу оптимизации с сотнями переменных и ограничений;
-
Решить её с использованием современных алгоритмов нелинейной оптимизации;
-
Проанализировать результаты через интерактивные визуализации и количественные метрики.
В данном примере мы не ограничиваемся теоретическими выкладками, а проходим через весь процесс — от исходных данных в формате Excel до готовых рекомендаций по оптимизации сети, сопровождая каждый шаг наглядными графиками и подробными объяснениями. Использование Julia, языка, сочетающего скорость C с выразительностью Python, делает решение одновременно эффективным и прозрачным.
Присоединим необходимые библиотеки.
using XLSX, JuMP, Ipopt, DataFrames, Graphs, SimpleWeightedGraphs, Colors, Printf, LinearAlgebra, Printf, GraphPlot
Присоединим необходимые файлы с функциями.
foreach(include, ("opti1.jl", "opti2.jl", "opti3.jl", "opti4.jl", "opti5.jl", "opti6.jl", "opti7.jl", "opti8.jl", "opti9.jl", "flowDir.jl", "optiwrite.jl", "lfwrite.jl"))
foreach(include, ("readqs.jl", "flowGraph.jl", "flGplot.jl", "netGraph.jl", "simpGraph.jl", "sGplot.jl","nGplot.jl"))
Структура СМО
Структуру системы массового обслуживания можно представить в виде квадратной матрицы сети с нулевой диагональю размером :
Где – количество узлов в сети, – суммарная пропускная способность каналов связи (ветвей графа), соединяющих узлы и направленных от узла с номером к узлу с номером , а нулевая диагональ подразумевает отсутствие каналов для потоков информации от узла, адресованных самому себе.
Направление потоков в системах массового обслуживания можно так же представить в виде квадратной матрицы с нулевой диагональю размером :
Где – количество узлов в сети, – величина потока, направленного от узла с номером к узлу с номером . Нулевая диагональ в матрице подразумевает отсутствие потоков от узла, адресованных самому себе.
Потоки и пропускные способности (ёмкости), могут быть представлены любой единицей измерения, применяемой в системах массового обслуживания, например: Мбит/c, количество продукции в час; количество товаров, перевозимых в сутки; количество транспорта, проезжаемого за час, количество заявок в сутки, и т.д..
Исходные данные
В нашем примере исходные данные представлены в виде xlsx-таблиц. NetMatrix.xlsx — пропускная способность и направление линий связи, FlowMatrix.xlsx — интенсивность и направление потоков.
Прочитаем исходные данные.
СМО = readqs("NetMatrix.xlsx", 1);
Потоки = readqs("FlowMatrix.xlsx", 1);
Отобразим ёмкости линий связи в виде матрицы.
display(СМО)
Отобразим потоки в виде матрицы.
display(Потоки)
На основании исходных данных, определим количество узлов, потоков, и линий связи в исследуемой СМО.
узлов = size(СМО, 1);
линий = count(!iszero, СМО);
потоков = count(!iszero, Потоки);
println("В системе массового обслуживания\n\nузлов: $узлов\nпотоков: $потоков\nлиний связи: $линий")
Визуализация СМО
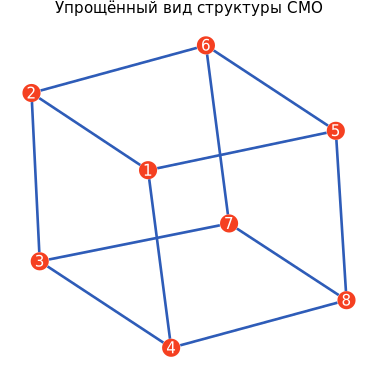
Отобразим структуру СМО в виде графа. Для наглядности на данном графе не будем учитывать направления и интенсивности линий связи.
и, п = simpGraph(СМО);
Граф = sGplot(и, п)
display(Граф)
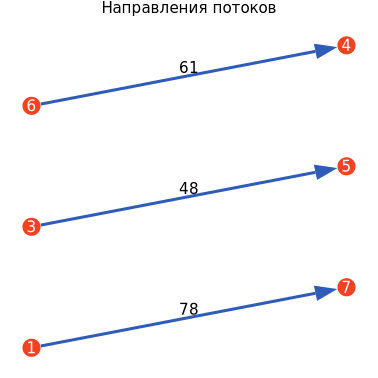
С помощью указания номеров узлов, величин интенсивности и стрелок, отобразим направления потоков.
nfl, nl, flG, flI = flowGraph(Потоки);
ГрафПотоков = flGplot(flG, flI, nl, "Направления потоков");
display(ГрафПотоков)
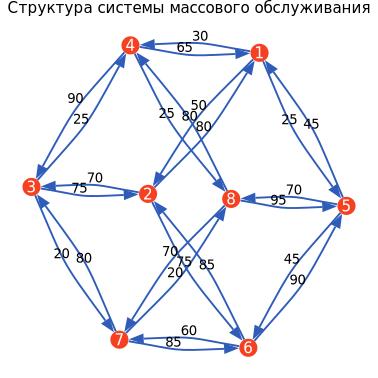
Теперь отобразим полную структуру СМО в виде направленного графа с указанием номеров узлов, направлений и ёмкостей линий связи.
s, t, bW = netGraph(СМО);
ГрафСМО = nGplot(s, t, bW, "Структура системы массового обслуживания");
display(ГрафСМО)
Система M/M/1
Рассмотрим систему M/M/1, в которой входящий поток заявок имеет пуассоновское распределение, а распределение времени обслуживания экспоненциальное, тогда среднее число заявок, находящихся в системе определяется формулой:
Где – интенсивность поступления заявок, – пропускная способность линий связи. Эта формула возникает из-за случайности в моментах прихода и обслуживания заявок. Когда система работает близко к пределу своей мощности (нагрузка приближается к 100%), даже небольшие случайные задержки начинают накапливаться, вызывая гиперболический, а не линейный, рост очереди. Математически это является следствием геометрического распределения количества заявок в системе, среднее значение для которого и определяется данным выражением. В дальнейшем на основании данной формулы будет формироваться целевая функция для оптимизаци.
Преобразование исходных данных
Для дальнейшего решения, преобразуем матрицу пропускных способностей в 3 вектора:
- список источников;
- список приёмников;
- список пропускных способностей (ёмкостей).
источник, приёмник, ёмкость = opti1(СМО, узлов, линий);
В процессе оптимизации для обхода загруженных линий связи, потоки могут разделиться на доли. Структуру долей потоков можно представить в виде системы матриц в количестве размера :
Где – количество узлов, – количество потоков, – величина доли потока номер , проходящая через линию, направленную от узла номер к узлу номер .
Матрица инцидентности
На основе матрицы смежности, создадим матрицу инцидентности.
Каждый столбец соответствует ветви графа: в строке источника ставится -1, в строке приёмника — +1. Матрица имеет размер узлов × линий и описывает, какие узлы соединены каждым ребром и направление линий.
МатрицаИнцидентности = opti2(узлов, линий, источник, приёмник);
display(МатрицаИнцидентности)
Ограничения потоков
Преобразуем матрицу потоков в 3 вектора:
-
список отправителей;
-
список получателей;
-
список интенсивностей потоков.
исток, приток, интенсивность = opti3(Потоки, узлов, потоков);
Создадим матрицу, обозначающую величины интенсивностей исходящих потоков из узлов-источников и входящих потоков в узлы-приёмники. Количество строк равно количеству узлов, а количество столбцов равно количеству потоков. Отрицательная величина обозначает исходящий поток из узла-источника, положительная величина обозначает входящий поток в узел-приёмник. Номера строк соответствуют номерам узлов.
исток_приток = opti4(узлов, потоков, исток, приток, интенсивность);
display(исток_приток)
Создадим трёхмерный массив, обозначающий направления потока в каждой линии связи. Количество строк равно двум (исток и приток), количество столбцов соответствует количеству линий связи линий, а количество двумерных матриц соответствует количеству потоков потоков. Данный массив будет использован для блокирования входящих потоков в узлы-источники и исходящих из узлов-приёмников.
ограничения = opti5(линий, потоков, источник, приёмник, исток, приток);
display(ограничения)
Уравнения и неравенства
На основе матрицы инцидентности и массива направления потоков, создадим трёхмерный массив, обозначающий знаки (-1 или 0 или +1) долей потоков для уравнений ограничений оптимизации СМО. Количество строк соответствует количеству узлов плюс два, так как в количестве равном количеству узлов обозначают ограничения в промежуточных линиях связи, а последние две в оконечных, которые блокируют входящие потоки в узлы-источники и исходящие из узлов-приёмников. Данные массивы будут использованы для создания уравнений ограничений оптимизации.
Уравнения = opti6(узлов, МатрицаИнцидентности, линий, потоков, ограничения, исток_приток);
display(Уравнения)
Поэлементно умножив полученный массив на переменные, обозначающие доли потоков, получим системы уравнений.
Рассмотрим, как формируется уравнение для узла 1, потока . Представляя доли потоков в виде матрицы:
Возьмём элемент матрицы с индексом , который равен нулю. Элементы первой строки подставляются в уравнение со знаком минус, элементы первого столбца подставляются в уравнение со знаком плюс. Получаем уравнение:
Для следующих узлов, возьмём индексы , и повторяем составление уравнений. Данные уравнения вводят ограничения, которые обозначают то, что сумма входящих и исходящих потоков в промежуточных узлах равна нулю.
Для наглядности, составим систему уравнений ограничений оптимизации в общем виде на примере узлов: и потока :
Где – количество узлов, – количество потоков.
Помимо систем уравнений, необходимым ограничением является максимальная интенсивность долей потоков в линиях связи, которая не должна превышать их пропускные способности. Для СМО, состоящей из 8 узлов и 24 линий связи, данное ограничение будет представлено следующей системой неравенств:
Преобразуем полученные результаты в исходные данные для выполнения задачи оптимизации.
А, Б, λ0, а, б = opti7(узлов, потоков, линий, Уравнения, исток_приток, ёмкость);
display(А)
display(Б)
Целевая функция
На основании структуры матрицы пропускных способностей и матрицы потоков, составим целевую функцию. Для СМО, состоящей из 8 узлов, 24 линий связи и 3 потоков, целевая функция будет иметь следующий вид:
Целевую функцию можно представить в общем виде:
где – значение среднего количества заявок в системе массового обслуживания, – количество линий связи – количество потоков, – величина пропускной способности линии связи, направленной от узла к узлу , – искомая оптимальная интенсивность доли потока направленного от узла к узлу , являющегося частью потока .
Задача оптимизации свидится к следующей цели: найти такие значения , при которых примет минимальное значение.
Оптимизация
Сформируем целевую функцию и выполним задачу оптимизации.
T, λ, нагрузка = opti8(А, Б, λ0, а, б, ёмкость, потоков);
Результаты оптимизации
Преобразуем данные для отображения в виде графов и вывода в виде xlsx-таблиц. И в случае успешной оптимизации, выведем матрицы оптимальных распределений потоков.
Оптимальные, НагрузкаСистемы = opti9(потоков, линий, λ, узлов, источник, приёмник, ёмкость);
if T #нагрузка > 0
display(Оптимальные)
end
Выведем результаты оптимизации.
nl = flowDir(Потоки);
if T
optiwrite(Оптимальные, потоков)
println("\nОптимизация выполнена.\n")
println("\nСреднее количество заявок в системе: $нагрузка\n")
else
println("\nОптимизация невыполнима при данных интенсивностях потоков и ёмкостях линий связи.\n")
end
Создадим xlsx-файл и выведем матрицу с коэффициентами загрузки линий связи.
lfwrite(НагрузкаСистемы)
display(НагрузкаСистемы)
Визуализация оптимальных потоков
Если оптимизация выполнена, отобразим оптимальное распределение интенсивностей потоков в виде графов.
if T
fnums = reshape(nl, (2, потоков));
for m in 1:потоков
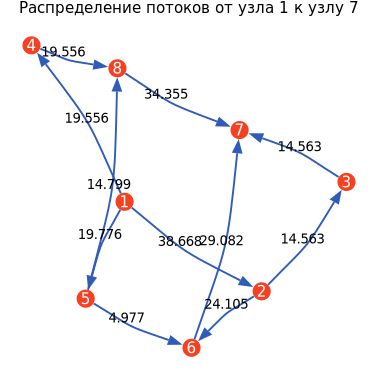
optiname = "Распределение потоков от узла $(fnums[1, m]) к узлу $(fnums[2, m])"
и, п, ё = netGraph(readqs("OptiFlows.xlsx", m));
ОптГраф(m) = nGplot(и, п, ё, optiname);
display(ОптГраф(m))
end
else
println("\nНеобходимо увеличить пропускные линий связи или уменьшить интенсивность потоков.\n")
end
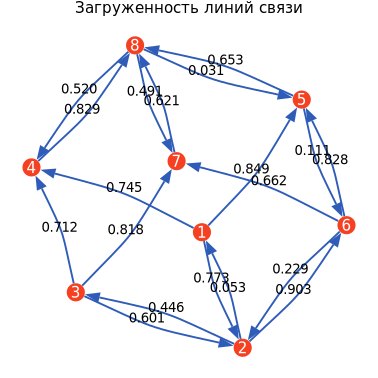
Визуализация загруженности линий
Отобразим коэффициенты загрузки линий связи в виде графа. На основании данного графа можно проанализировать, требуется ли определённым линиям связи увеличение пропускной способности. В случае, если оптимизация невыполнима при данной пропускной способности линий связи, коэффициенты загрузки, превышающие единицу обозначают во сколько раз нужно увеличить данную линию связи для того, чтобы оптимизация стала возможной.
lM = readqs("LoadFactors.xlsx", 1);
s1, t1, bW1 = netGraph(lM);
ГрафНагрузки = nGplot(s1, t1, bW1, "Загруженность линий связи");
display(ГрафНагрузки)
Помимо представленных графов, в качестве результатов вычислений, мы получили xlsx-таблицы с матрицами оптимального распределения потоков (OptiFlows.xlsx) и загруженности линий связи при данных величинах потоков и ёмкостях линий связи (LoadFactors), которые будут удобны в использовании для дальнейших вычислений и исследований.
Оптимизируйте собственную систему
С помощью представленного алгоритма вы можете оптимизировать вашу собственную систему массового обслуживания, для этого:
-
Подготовьте двух стандартизированных файлов в формате Excel:
-
NetMatrix.xlsx— матрица направлений и пропускных способностей линий связи -
FlowMatrix.xlsx— матрица направлений и интенсивностей обслуживаемых потоков
-
-
Загрузите их в интерактивную вычислительную среду
-
Инициируйте аналитический процесс с получением комплексного результата:
-
Матрицы оптимального распределения для каждого потока
-
Графическое представление коэффициентов загрузки каналов
-
Визуализация топологии сети и конфигурации потоков
-
Количественные показатели параметров системы
-
Вне зависимости от масштаба и специфики системы — будь то муниципальная транспортная инфраструктура, корпоративная вычислительная сеть или производственно-логистический комплекс — представленный инструмент обеспечивает адаптивный анализ на основе предоставленных данных. Методология позволяет идентифицировать критические элементы, работающие на пределе пропускной способности, выявлять недостаточно загруженные маршруты и определять оптимальные схемы распределения потоков.
Следует отметить, что оптимизация сетевых структур более не является исключительной компетенцией специалистов с доступом к специализированному программному обеспечению. В настоящее время это становится стандартизированной процедурой, в которой сложные вычислительные алгоритмы реализованы в интуитивно понятном интерфейсе, а глубина аналитики органично сочетается с наглядностью представления.
Рекомендуется апробация методологии на актуальных данных. Загрузка матриц конкретной системы в среду Engee позволит наблюдать практическую реализацию принципов теории массового обслуживания, обнаруживать скрытые резервы в существующих конфигурациях и находить эффективные решения для оптимизационных задач.
Следует рассматривать оптимизацию не как разовое мероприятие, а как непрерывный процесс совершенствования. Представленный инструментарий обеспечивает его системность, наглядность и результативность, формируя основу для принятия обоснованных управленческих решений в условиях динамичной среды функционирования сложных сетевых систем.
Заключение
Настоящее исследование продемонстрировало методологический переход от фундаментальных принципов теории массового обслуживания к практической реализации комплексной оптимизации сетевых структур. На примере системы, включающей 8 узлов, 24 канала связи и 3 потока обслуживания, была проиллюстрирована трансформация математических концепций — пуассоновских потоков, экспоненциальных распределений, матриц смежности и инцидентности — в эффективный инструментарий решения прикладных задач. Модель M/M/1, являющаяся классическим объектом теоретического рассмотрения, была успешно применена в качестве основы для построения целевой функции, минимизирующей среднее количество заявок в распределённой сети.
Центральный результат проведённой работы заключается в демонстрации того, что оптимизация сетевых структур представляет собой системный процесс с четко определёнными этапами: математическое моделирование, визуальное представление, формализация ограничений, численное решение и аналитическая интерпретация результатов. Экспериментально подтверждено, что даже в сетях умеренной сложности информационные потока закономерно распределяются по альтернативным маршрутам, демонстрируя адаптивность к потенциальным перегрузкам критических элементов. Визуализация результатов посредством направленных графов обеспечила не только представление итоговых значений, но и понимание причинно-следственных связей в системе.
Наиболее значимым аспектом является практическая доступность представленной методологии. Для специалистов, решающих задачи проектирования телекоммуникационных сетей, оптимизации логистических маршрутов, распределения вычислительных ресурсов или управления информационными потоками, предлагается готовое инструментальное решение.
.png)
.png)