Engee Community
/
Примеры и проекты
/
Основы ЦОС: спектральный анализ

Основы ЦОС: спектральный анализ

Автор
avatar-ussmoussmo
Notebook

Основы ЦОС: спектральный анализ

В цифровой обработке сигналов (ЦОС) спектральный анализ — это набор методов, позволяющих разложить сигнал на частотные компоненты и исследовать его свойства в частотной области.

Основные задачи спектрального анализа в ЦОС:

  1. Определение частотного состава сигнала (например, выделение тональных компонент в аудиосигнале).

  2. Обнаружение скрытых периодичностей (например, анализ вибраций в механических системах).

  3. Спецификация фильтров (для последующего удаления шумов, выделения полезных частот).

  4. Сжатие данных (использование частотных представлений, таких как JPEG, MP3).

  5. Распознавание паттернов (например, анализ речевых сигналов).

В качестве основных методов анализа применяются:

  • Дискретное преобразование Фурье (ДПФ) и быстрое преобразование Фурье (БПФ). Подробнее о БПФ - в этом примере.

  • Периодограмма (оценка спектра мощности)

  • Метод Уэлча (усредненная периодограмма)

  • Параметрические методы (авторегрессия, AR)

  • Банк фильтров

В данном примере мы рассмотрим методы БПФ, периодограммы и Уэлча для задачи анализа аудиосигнала.

In [ ]: 
# Это нужно выполнить, если не установлены необходимые библиотеки
#Pkg.add("DSP")
#Pkg.add("WAV")
#Pkg.add("Base64")
#Pkg.add("FFTW")
#Pkg.add("FindPeaks1D")
#Pkg.add("Statistics")
In [ ]: 
using DSP, WAV, Base64, FFTW, FindPeaks1D, Statistics

Исходный сигнал для анализа

В качестве тестового сигнала мы берём аудиозапись гитарной струны. Наша задача - определить, что за нота проигрывается, анализируя спектр сигнала.

Загрузим численные отсчёты сигнала функцией wavread, которая также позволяет выделить частоту дискретизации сигнала fs.

In [ ]: 
filename = "$(@__DIR__)/guitar.wav"
audio_data, fs = wavread(filename);

Подсчитаем количество отсчётов сигнала во временной области, вычислим временной шаг и сформируем вектор времени:

In [ ]: 
nsamples = length(audio_data);
dt = 1/fs;
t = 0:dt:((nsamples - 1) .* dt);
sig = vec(audio_data);

Для прослушивания аудио воспользуемся дополнительной функцией audioplayer:

In [ ]: 
function audioplayer(s, fs);
    buf = IOBuffer();
    wavwrite(s, buf; Fs=fs);
    data = base64encode(unsafe_string(pointer(buf.data), buf.size));
    markup = """<audio controls="controls" {autoplay}>
                <source src="data:audio/wav;base64,$data" type="audio/wav" />
                Your browser does not support the audio element.
                </audio>"""
    display("text/html", markup);
end
Out[0]:
audioplayer (generic function with 1 method)

Прослушаем звук колеблющейся струны:

In [ ]: 
audioplayer(sig,fs)

Наконец, отобразим сигнал во временной области:

In [ ]: 
plot(t, sig,
    xguide = "Время, с", 
    yguide = "Амлпитуда, В",
    title = "Аудиосигнал во времени",
    legend = false)
Out[0]:

Узнать основную частоту колебания по форме периодического сигнала во временной области можно, но всё же весьма затруднительно.

Оценка спектра сигнала

Рассмотрим три метода для построения спектра мощности или графика спектральной плотности мощности (СПМ) тестового сигнала. Для качественного анализа частотного состава подходят обе метрики.

Начнём с построения спектра мощности на основе БПФ. Подробнее о функциях и математике - в предыдущем примере.

In [ ]: 
A = fft(sig);
B = fftshift(A);
df = fs/nsamples;
freq_vec = -fs/2:df:fs/2-df;
plot(freq_vec, pow2db.(abs.(B.^2)),
    xguide = "Частота, Гц", 
    yguide = "Мощность, дБ",
    title = "Спектр мощности сигнала (на основе БПФ)",  
    xlim = (0,10000),
    legend = false)
Out[0]:

На спектре явно прослеживается гармоническая структура - равнорасположенные пики. Гармоники - это синусоидальные колебания, частоты которых кратны основной частоте ​$f_0$.

$f_0$ - самая низкая частота в сигнале (первая гармоника), а высшие гармоники - частоты вида $n⋅f_0$​, где $n=2,3,4,…$ (вторая, третья и т. д.).

Периодограмма

Периодограмма — это метод оценки спектральной плотности мощности (СПМ) сигнала на основе его дискретного преобразования Фурье (ДПФ). На практике вычисляется через БПФ.

Алгоритм:

  1. Берётся отрезок сигнала (например, 1024 отсчёта).

  2. Вычисляется БПФ этого отрезка.

  3. Возводится амплитудный спектр в квадрат и нормируется на длину выборки.

  4. Получается график мощности по частотам.

In [ ]: 
p1 = DSP.periodogram(sig, onesided=true, fs=fs);
plot(freq(p1), pow2db.(power(p1)), 
    xguide = "Частота, Гц", 
    yguide = "Мощность/частота, дБ/Гц",
    title = "Спектральная плотность мощности сигнала (периодограмма)",
    xlim = (0,10000),
    legend = false)
Out[0]:

Впрочем, у этого метода есть ряд недостатков:

  • Высокая дисперсия – оценка "скачет" при небольших изменениях данных.

  • Утечка спектра (leakage) – из-за конечной длины сигнала возникают ложные частоты (решается оконными функциями, например, Ханна или Хэмминга).

  • Низкое частотное разрешение – если сигнал короткий, близкие частоты сливаются.

Метод Уэлча

Метод Уэлча - это модификация периодограммы, в которой:

  • Сигнал разбивается на перекрывающиеся отрезки.

  • К каждому отрезку применяется оконная функция (например, Ханна, Хэмминга) - это уменьшает эффект утечки спектра.

  • Для каждого отрезка считается периодограмма.

  • Результаты усредняются → снижается дисперсия.

In [ ]: 
p2 = DSP.welch_pgram(sig, onesided=true, fs=fs);
plot(freq(p2), pow2db.(power(p2)), 
    xguide = "Частота, Гц", 
    yguide = "Мощность/частота, дБ/Гц",
    title = "Спектральная плотнотсть мощности сигнала (метод Уэлча)",
    xlim = (0,10000),
    legend = false)
Out[0]:

Определение основной частоты сигнала

Остановимся на оценке СПМ методом Уэлча и проанализируем область низких частот (от 0 до 1500 Гц). Найдём пики в спектре - они соответствуют гармоникам сигнала. В этом нам поможет функция findpeaks1d из соответствующего пакета. Выделим первые шесть гармоник, и отобразим их на графике:

In [ ]: 
spectrum = pow2db.(power(p2));
fvec = freq(p2);
pkindices, properties = findpeaks1d(spectrum; 
                                    height = -65,
                                    prominence = 20);
plot(fvec, spectrum, 
    linewidth = 3,
    xguide = "Частота, Гц", 
    yguide = "Мощность/частота, дБ/Гц",
    title = "Пики спектра сигнала (метод Уэлча)",
    xlim = (0,1500),
    label = "спектр")
scatter!(fvec[pkindices], spectrum[pkindices]; color="red", markersize=5, label="пики")
Out[0]:

Самый первый пик находится на частоте 219 Гц. Но мы также можем программно определить частоты первых шести гармоник и найти среднее расстояние между ними в Гц. Именно эту оценку мы и примем за основную частоту:

In [ ]: 
harmonics = fvec[pkindices[1:6]]
Out[0]:
6-element Vector{Float32}:
  219.375
  438.75
  658.125
  877.5
 1102.5
 1321.875
In [ ]: 
base_freq = mean(diff(harmonics))
Out[0]:
220.5f0

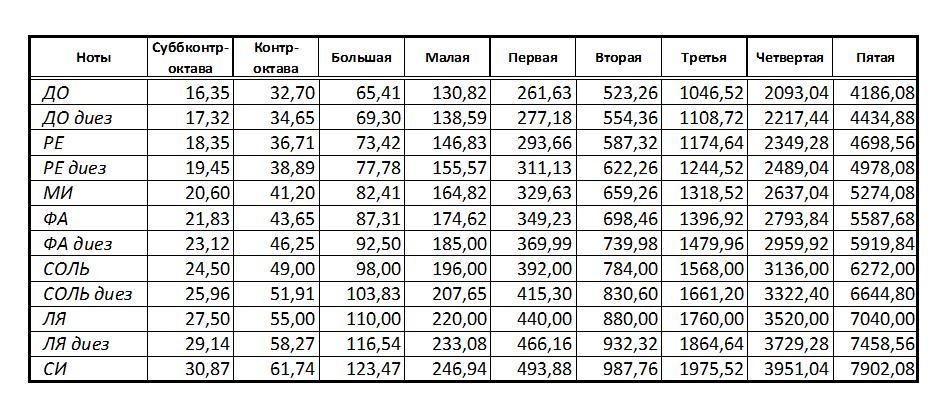
image.png

Судя по таблице, сыгранная нота - это Ля малой октавы.

Выделение первой гармоники

Синтезируем простой эллиптический фильтр нижних частот (ФНЧ), подавляющий частоты выше 300 Гц. Это позволит нам отсечь высшие гармоники. Отфильтруем исходный сигнал и прослушаем результат:

In [ ]: 
myfilt = digitalfilter(Lowpass(2*300/fs), Elliptic(10, 0.1, 80));
clean220 = filt(myfilt, sig);
audioplayer(clean220 * 2, fs)

Мы слышим более "чистый" тон, лишённый окраса. В нём не сразу можно узнать гитару, так как тембр инструменту придают именно высшие гармоники.

Заключение

Мы рассмотрели три стандартных метода оценки спектра сигнала - БПФ, периодограмму и метод Уэлча на примере анализа частотного состава аудиосигнала колеблющейся гитарной струны, - а также определили основную частоту колебания.

Группа видимости
ПубличноПросматривать контент могут все пользователи сообщества

Тип

Интерактивные скрипты

Краткое описание

Знакомство с базовыми методами спектрального анализа на примере оценки частотного состава звука гитарной струны.

Связанные материалы

Пусто

Теги

Категории

Отраслевые примененияОбработка сигналов

Языки

    Julia

Форматы

    ngscript

Уровень

    Базовый

Статус

Опубликовано

Обновлено

Источник

Engee