Оценка оптимальной ставки налога на прибыль.

В данном примере покажем, как оценить оптимальную ставку налога на прибыль методами имитационного моделирования, на основе использования Julia + Engee. Поиск решения будем осуществлять на сетке факторов. Планирование экспериментов заключается в изменении факторов (ставка налога,рентабельность предприятия) с постоянным шагом и построении экспериментальных графиков зависимости значения критерия оптимальности (доход государства) от факторов. Оптимальные величины ставки налога оценивается визуально по графикам.

Определение проблемы

Государство стремиться увеличить налоги, чтобы пополнить бюджет.

Бизнес желает уменьшения налоговых ставок.

Экономисты утверждают,что большие налоги сдерживают развитие экономики, а значит и будущее наполнение бюджета.

Проблема: теория и практика не знают величины приемлемой для всех налоговой ставки.

Задача обосновать величину налоговой ставки.

Рабочая гипотеза Поступления в бюджет за определенный период времени будет наибольшим не при максимальной, а при оптимальной для бюджета ставке налога. То есть с ростом налоговой ставки сначала поступления в бюджет будут увеличиваться, а затем уменьшаться.

Вербальная модель

Государство объявляет ставку налога на прибыль и получает от фирм средства в бюджет. Фирмы обладают собственным капиталом, производят прибыль, отчисляют по налоговой ставке средства в бюджет. Постналоговая прибыль полностью включается в собственный капитал фирмы. Дивиденды не выплачиваются, никаких других отчислений от прибыли не производиться. Вся прибыль распределяется только на два потока: в бюджет, а остаток-в собственный капитал фирмы.

Математическая модель

Приведенная выше вербальная модель, формально может быть представлена в непрерывном формате следующим образом:

Имитационные компьютерные модели.

Перейдем от непрерывного формата модели к дискретному. При этом в качестве исходных данных будут использоваться: значение налоговой ставки, рентабельность, начальный капитал фирм и интервал моделирования.

Рассмотрим два варианта имитации экономического процесса на базе дискретной модели.

1. Имитационные эксперименты на основе использования Engee модели Nalog.

Engee модель Nalog имеет следующий вид:

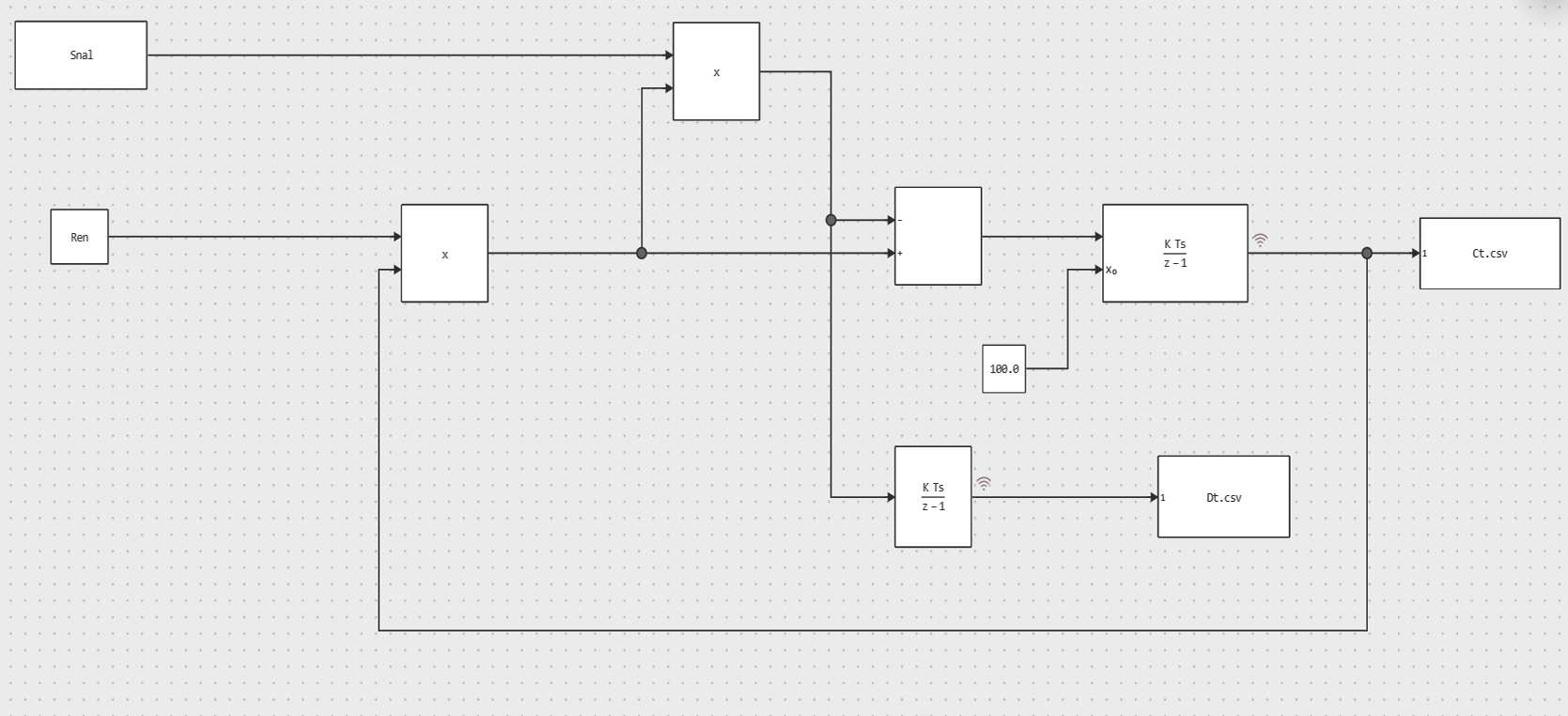
Имитационный эксперимент с этой моделью реализуется с помощью следующего скрипта Julia:

#Программа исследования влияния ставки налога на доходы государства
using RDatasets, Plots, PlotThemes
using CSV,DataFrames

D=zeros(4,10)
nal=(0.1:0.1:1.0)
rentab=(0.2:0.2:0.8)

#открытие модели
modelName = "Nalog";
PID_model = modelName in [m.name for m in engee.get_all_models()] ? engee.open(modelName) :
            engee.load("/user/Nalog/$(modelName).engee");
engee.set_param!(modelName, "StopTime" => 10.0) # задание интервала моделирования

#План 'эксперимента по рентабельности
for i in (1:4)
    Ren=rentab[i]
#План эксперимента по ставке налога 
    for j in (1:10)
        Snal=nal[j]
#Выполнение модели
        engee.run(modelName)
        df_Dt=CSV.read("Dt.csv",DataFrame)
        D[i,j]=df_Dt[end,2]
    end    
end    

D

4×10 Matrix{Float64}:
   47.0426    85.2859   116.024  …   184.531   192.098   197.095  200.0
  229.406    376.494    463.111      491.365   463.57    432.22   400.0
  822.502   1235.54    1385.73       987.895   842.339   711.763  600.0
 2506.81    3493.67    3615.36      1772.03   1364.57   1043.03   800.0

#Построение графиков
theme(:dao)
plot(nal, D[1,:], label="Ren=0.2", linewidth=3)
plot!(nal, D[2,:], label="Ren=0.4", linewidth=3)
plot!(nal, D[3,:], label="Ren=0.6", linewidth=3)
plot!(nal, D[4,:], label="Ren=0.8", linewidth=3)
ylabel!("Поступление в бюджет")
xlabel!("Налоговая ставка")
title!("Определение оптимальной налоговой ставки (T=10)")

2. Имитационные эксперименты без использования Engee модели Nalog.

Имитационный эксперимент в этом случае реализуется с помощью следующего скрипта Julia:

#Определение оптимальной налоговой ставки
#Двухфакторный дискретный эксперимент, интервал исследования Т=10 
using Plots, PlotThemes

Ct=zeros(11)
Cpt=zeros(11)
Bd = zeros(11)
Bdsum=zeros(4,10)
K0=100  # исходный капитал
i=0
for Ren in (0.2:0.2:0.8) 
    j=0
    i=i+1
    for Snal in (0.1:0.1:1.0)
        j=j+1
        
       
        Cpt[1]=K0
        
        for t in (2:11)
           Ct[t]=Cpt[t-1]*Ren
           Cpt[t] =Ct[t]*(1-Snal)+Cpt[t-1]
           Bd[t] =Bd[t-1]+Ct[t]*Snal
           
        end
        Bdsum[i,j]=Bd[11]
    end
end

Ren = (0.2:0.2:0.8);
renlab1 = "Ren= "*string(Ren[1])
renlab2 = "Ren= " *string(Ren[2])
renlab3 = "Ren= " *string(Ren[3])
renlab4 = "Ren= " *string(Ren[4])

Bdsum

4×10 Matrix{Float64}:
   47.0426    85.2859   116.024  …   184.531   192.098   197.095  200.0
  229.406    376.494    463.111      491.365   463.57    432.22   400.0
  822.502   1235.54    1385.73       987.895   842.339   711.763  600.0
 2506.81    3493.67    3615.36      1772.03   1364.57   1043.03   800.0

#plotly()
theme(:dao)
Snal = (0.1:0.1:1.0)
plot(Snal, Bdsum[1, :], label=renlab1, legend=:topright, wsize=(800, 500), linewidth=3)
plot!(Snal, Bdsum[2, :], label=renlab2, linewidth=3)
plot!(Snal, Bdsum[3, :], label=renlab3, linewidth=3)
plot!(Snal, Bdsum[4, :], label=renlab4, linewidth=3)
ylabel!("Поступление в бюджет")
xlabel!("Налоговая ставка")
title!("Определение оптимальной налоговой ставки (T=10)")

Построенные в результате компьютерного имитационного эксперимента графики, позволяют оценивать оптимальную для бюджета ставку налога на прибыль для разных значений уровня рентабельности фирм.

Рассмотренный экономический пример взят из книги: И.Ф. Цисарь., В.Г.Нейман "Компьютерное моделирование экономики" .

Оценка оптимальной ставки налога на прибыль