Оценка параметров движения с помощью фильтра Калмана

В данном примере рассмотрен способ оценки параметров состояния линейной системы с помощью дискретного фильтра Калмана.
В качестве объекта управления используется автомобиль, текущие координаты которого определятся с помощью датчика положения, основанного, например, на сигнале от ГНСС (ГЛОНАСС/GPS).
На основании этих данных формируется оценка текущего положения и скорости автомобиля.
Стоит отметить, что показания датчика положения в силу тех или иных причин искажены от истинных (зашумлены).

Введение

Движение автомобиля упрощённо рассматривается как плоское движение материальной точки.
Какие-либо препятствия, мешающие передвижению автомобиля, отсутствуют.
Положение и скорость автомобиля определяются в системе координат , где центр масс автомобиля имеет координаты .

Для описания движения автомобиля также необходимо ввести понятие угла , который показывает поворот продольной оси автомобиля относительно оси , и угла поворота автомобиля

Разработанная модель навигационно-управляющей системы может быть использована для любого объекта управления, не обязательно автомобиля.
Модель состоит из двух основных частей: математической модели объекта и его системы управления, и дискретного фильтра Калмана.

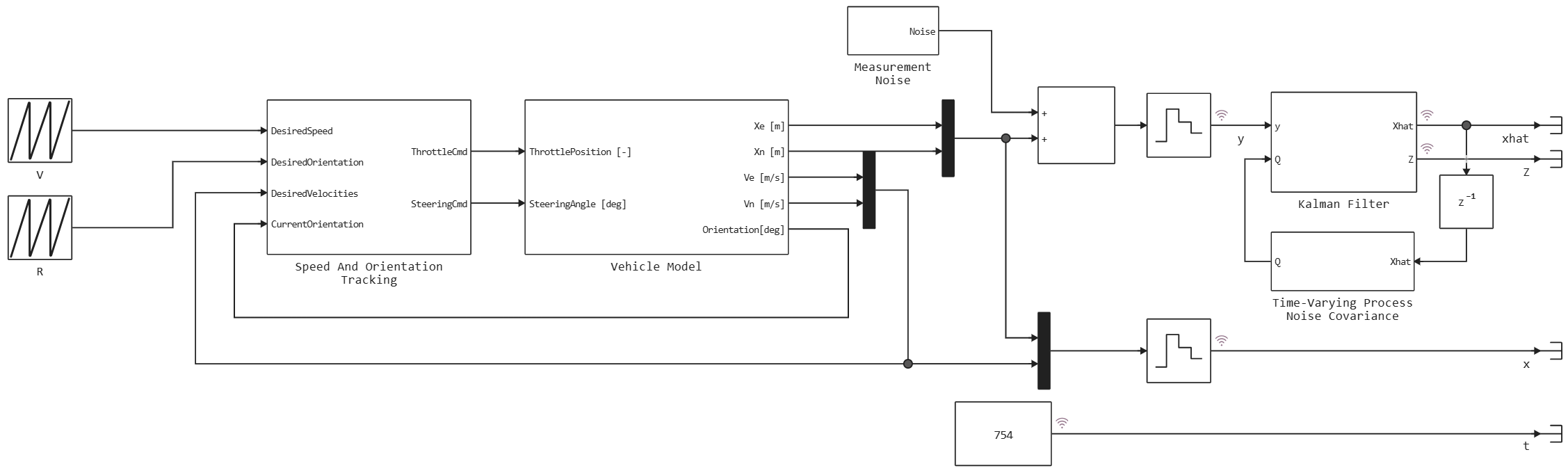
Модель автомобиля

Модель движения центра масс автомобиля:

где параметры состояний автомобиля:

- восточная координата, м;

- северная координата, м;

- скорость, м/с;

- направление относительно востока, град.

параметры автомобиля:

- максимальная мощность двигателя, Вт;

- площадь фронтальной поверхности, ;

- коэффициент лобового сопротивления, безразмерный;

- масса автомобиля, кг;

- длина колёсной базы, м.

характеристики входных сигналов:

- сигнал управления дроссельной заслонкой двигателя в диапазоне , безразмерный;

- угол поворота автомобиля, град.

Динамика модели в продольном канале не учитывает сопротивление качению шин.
Момент инерции рысканья отсутствует, поэтому при повороте угол будет достигаться мгновенно.

Математическая модель автомобиля представлена в подсистеме Vehicle model.

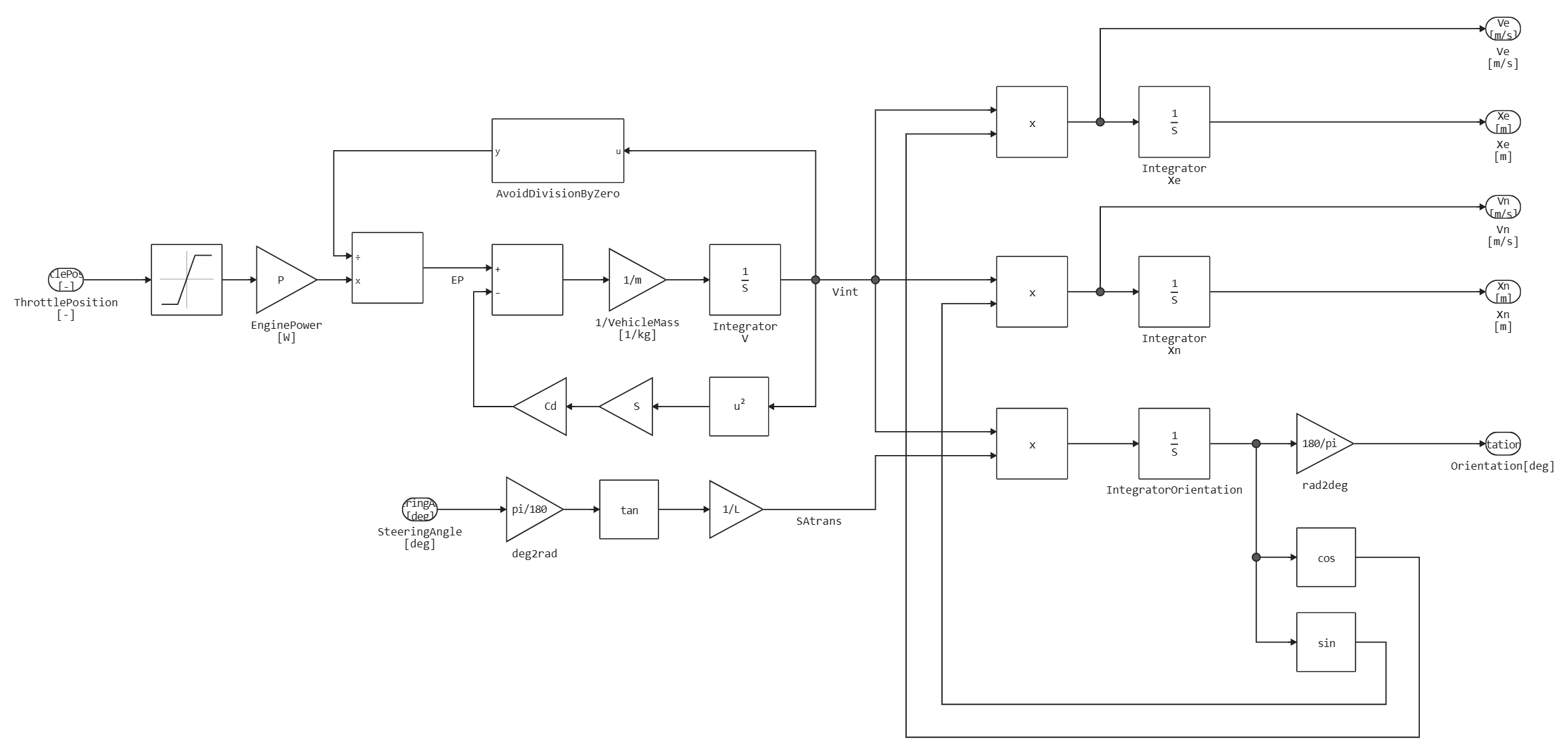
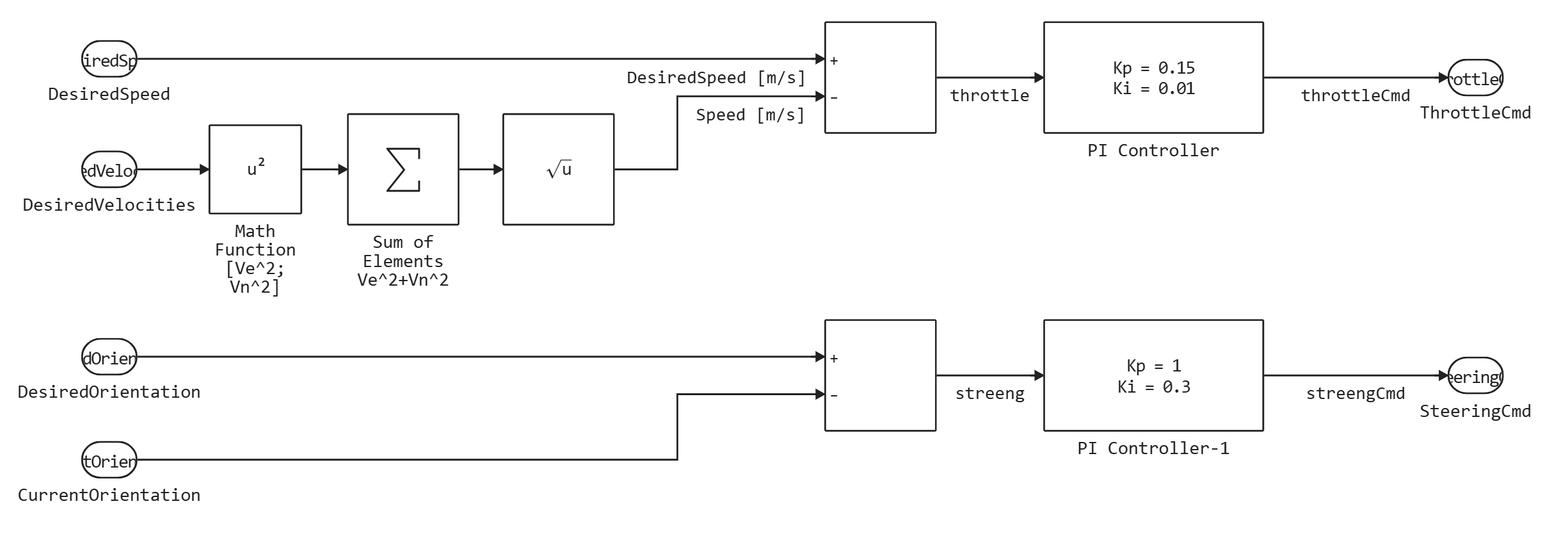
Модель системы управления находится в подсистеме Speed orientation and tracking.
Основу этой модели составляют два ПИ-регулятора. Настройкой этих регуляторов можно добиться разной динамики объекта управления и таким образом проверить результативность фильтра Калмана в различных сценариях работы.

Модель дискретного фильтра Калмана

Фильтр Калмана - это алгоритм оценки неизвестных параметров какого-либо объекта на основании его линейной модели.
Линейная модель описывает эволюцию оцениваемых параметров во времени с учётом известных начальных условий и неизвестных внешних воздействий.
В данном примере рассмотрена оценка следующих параметров:

где

- оценка восточной координаты, м;

- оценка северной координаты, м;

- оценка составляющей скорости на восток, м/с;

- оценка составляющей скорости на север, м/с.

Параметры обозначают скорость, а не оператор производной. - это индекс дискретного момента времени.

Модель дискретного фильтра Калмана представлена в следующей форме:

\begin{array}{rl}
\hat{x}[n+1] =& A \hat{x}[n] + Gw[n] \
y[n] =& C\hat{x}[n] + v[n]
\end

здесь

- вектор состояний;

- вектор измерений;

- нормальный случайный процесс,
описывающий случайный характер изменений системы;

- белый гауссовский шум измерений.

Алгоритм фильтра Калмана предполагает, что математические ожидания случайных процессов и были равны .
Эти процессы зависят от случайных величин с известными значениями дисперсий , и .
В нашем примере матрицы , и будут равны:

где время дискретизации с.

Третья строка матриц и моделируют компоненту скорости по восточной оси как случайный процесс:

В реальности положение является непрерывной функцией и определяется как интеграл от скорости по времени

Первая строка матриц и представляют собой дискретную аппроксимацию уравнения движения:

Аналогичные действия по отношению к северной координате и компоненте скорости описаны во второй и четвёртой строчках матриц и .

Матрица описывает только доступные измерению параметры.
Датчик предоставляет данные положения с частотой Гц.
Дисперсия шума измерений известна, и определена как .
Математически необходимо, чтобы значение дисперсии было преобразовано из скаляра в матрицу, где на диагонали будут значения дисперсии , а размерность этой матрицы будет согласована с размерностью вектора измерений .

Для шума, который распределён по гауссовскому (нормальному) закону, с дисперсией , измеренные с помощью датчика координаты автомобиля с вероятностью попадут в диапазон м от его реального положения в обоих направлениях. Впрочем, это допущение не является обязательным для работы фильтра Калмана.

Характеристики случайного процесса показывают насколько сильно может измениться скорость за дискретный момент времени .
Ковариационная матрица состоит из дисперсий процесса , представленных функциями времени.
Для их описания также применяется функция насыщения .

На диагонали матрицы функции дисперсий случайного процесса обратно пропорциональны квадратам оценённых значений скоростей . Таким образом наиболее вероятные значения тем меньше, чем больше скорость.

Пример: увеличить скорость с до м/с проще, чем увеличить скорость с до м/с.

Функция насыщения не даёт значениям дисперсии становиться слишком маленькими, или, наоборот, слишком большими.
Коэффициент в числителе получен методом наименьших квадратов для данных о времени ускорения до скоростей , , , , м/с, которых обычно достигают автомобили.

Важно отметить, что данный вид ковариационной матрицы получен на основании допущения, что взаимная корреляция между составляющими скоростей отсутствует.

Математическая модель фильтра Калмана реализована в подсистеме Kalman Filter, а ковариационная матрица формируется в подсистеме Time-Varing Process Noise Covariance

Моделирование

Для работы с моделью и обработки данных требуется подключение пакетов расширения:

# Добавление отсутствующих пакетов
Pkg.add(["MATLAB", "CSV", "DataFrames", "Statistics", "LinearAlgebra"]);

# Подключение необходимых пакетов
using Plots
using MATLAB
using CSV
using DataFrames
using Statistics
using LinearAlgebra

Применение макроса @__DIR__ необходимо для определения дескриптора пути к файлам:

demoroot = @__DIR__;

Проверка работы фильтра Калмана будет осуществляться с помощью моделирования сценария, в котором автомобиль совершает следующие манёвры:

В момент времени автомобиль находится в координатах , и стоит на месте.
Автомобиль начинает движение на восток и ускоряется до м/с. В момент времени с автомобиль замедляется до м/с.
В момент времени с он поворачивает на север и ускоряется до м/с.
В момент времени с автомобиль делает поворот на запад и ускоряется до м/с.
В момент времени с автомобиль замедляется до м/с и с постоянной скоростью делает разворот на градусов.

С помощью скрипта считаем данные из CSV-файла KF_data.csv и определим необходимые для моделирования переменные:

# Загрузка данных маршрута движения из CSV-файла 
KF_data = CSV.read("$demoroot/KF_data.csv", DataFrame; delim = ",", header = 1);

# Определение переменных
t = KF_data.tt; # Время, с
r = KF_data.rr; # Направление движения (Theta), град
v = KF_data.vv; # Скорость, м/с

Визуализируем полученные данные:

#gr()        # Отключение интерактивности при построении графиков (легче для отрисовки)
plotlyjs() # Включение интерактивности (сложнее для отрисовки)
plot(t, [r, v],
label = ["Направление, град" "Скорость, м/с"], lw = 2)
plot!(xlabel = "Время, с", legend=:topleft, title = "Сценарий моделирования")

Зададим параметры объекта управления (автомобиля) и начальные условия:

# Параметры автомобиля
P = 1e5;      # Максимальная мощность двигателя, Вт
S = 1.0;      # Площадь фронтальной поверхности, м^2
Cd = 0.3;     # Коэффициент лобового сопротивления, безразмерный  
m = 1250.0;   # Масса автомобиля, кг
L = 2.5;      # Длина колёсной базы, м

# Начальные условия
xe0 = 0.0;    # Начальная координата xe, м
xn0 = 0.0;    # Начальная координата xn, м
V0 = 0.0;     # Начальная скорость, м/с
theta0 = 0.0; # Начальное направление движения, рад

А также определим параметры фильтра Калмана:

# Параметры фильтра Калмана

Ts = 1;           # Время дискретизации, с
u = 0.0;          # Входной сигнал отсутствует
isEnabled = true; # Всегда обновлять измерения   

#  Матрицы A, B, C, D модели объекта управления
## Матрица состояний
A = [1.0 0.0 Ts 0.0; 
     0.0 1.0 0.0 Ts; 
     0.0 0.0 1.0 0.0; 
     0.0 0.0 0.0 1.0];
## Матрица входных сигналов 
B = [0.0; 
     0.0; 
     0.0; 
     0.0];
## Матрица выходных сигналов
C = [1.0 0.0 0.0 0.0; 
     0.0 1.0 0.0 0.0];
## Матрица feedthrough-сигналов
D = [0.0; 
     0.0];

# Матрица измерений
G = [Ts/2.0 0.0; 
     0.0 Ts/2.0; 
     1.0 0.0; 
     0.0 1.0];

# Матрица H показывает влияние
# процесса w на измерения y
H = [0.0 0.0; 
     0.0 0.0];

# Матрица N показывает корреляцию 
# между шумом процесса и шумом измерения
N = [0.0 0.0; 
     0.0 0.0];

# Матрица дисперсии шума измерений R 
R = [50.0 0.0; 
     0.0 50.0]

# Начальные условия для положения и ускорения
X0 = [xe0; 
      xe0; 
      V0 * cos(theta0); 
      V0 * sin(theta0)];

# Ковариация ошибки оценки состояния
P0 = [10.0 10.0 10.0 10.0; 
      10.0 10.0 10.0 10.0; 
      10.0 10.0 10.0 10.0; 
      10.0 10.0 10.0 10.0]

# Ограничения функции насыщения 
fsat_max = 625; # верхний предел 
fsat_min = 25;  # нижний предел

Откроем модель и запустим симуляцию:

# Загрузка модели Engee, если она еще не открыта на холсте
if "Kalman_navigation" ∉ getfield.(engee.get_all_models(), :name)
    engee.load( "$demoroot/Kalman_navigation.engee");
end

# Запуск симуляции модели Engee
model_data = engee.run("Kalman_navigation");

Извлечём данные, полученные в ходе симуляции:

t_d = model_data["t"].time;  # Время симуляции в цифровом формате [Ts = 1]

# Зашумлённые значения измеренных координат
y = model_data["y"].value;    
ye = zeros(Float64, length(y));
for i = 1:length(y)
    ye[i] = y[i][1];
end

yn = zeros(Float64, length(y));
for i = 1:length(y)
    yn[i] = y[i][2];
end

# Значения координат и скорости
x = model_data["x"].value; 
xe = zeros(Float64, length(x));
for i = 1:length(x)
    xe[i] = x[i][1];
end

xn = zeros(Float64, length(x));
for i = 1:length(x)
    xn[i] = x[i][2];
end

Ve = zeros(Float64, length(x));
for i = 1:length(x)
    Ve[i] = x[i][3];
end

Vn = zeros(Float64, length(x));
for i = 1:length(x)
    Vn[i] = x[i][4];
end

# Значения оценки координат и скорости
xhat = model_data["xhat"].value; 
xe_hat = zeros(Float64, length(xhat));
for i = 1:length(xhat)
    xe_hat[i] = xhat[i][1];
end

xn_hat = zeros(Float64, length(xhat));
for i = 1:length(xhat)
    xn_hat[i] = xhat[i][2];
end

Ve_hat = zeros(Float64, length(xhat));
for i = 1:length(xhat)
    Ve_hat[i] = xhat[i][3];
end

Vn_hat = zeros(Float64, length(xhat));
for i = 1:length(xhat)
    Vn_hat[i] = xhat[i][4];
end

Построим действительное, измеренное и оцененное значения положения автомобиля как траекторию его движения:

#gr()      # Отключение интерактивности при построении графиков (легче для отрисовки)
plotlyjs() # Включение интерактивности (сложнее для отрисовки)
plot([xe, ye, xe_hat], [xn, yn, xn_hat],
label = ["Действительное положение" "Измеренное" "Оценка"], lw = 1.5, c = ["blue" "red" "green"])
plot!(xlabel = "Восток, м", ylabel = "Север, м",
legend=:topleft, title = "Положение")

Для того чтобы дать качественную оценку работы фильтра Калмана, произведём расчёт ошибок измерения датчика и оценки фильтра в сравнении с действительными значениями координаты и скорости:

# Ошибки измерения координат, м
n_xe = ye - xe;
n_xn = yn - xn;

# Ошибки оценок координат фильтром Калмана, м
e_xe = xe_hat - xe;
e_xn = xn_hat - xn;

# Ошибки оценок скорости фильтром Калмана, м/с
e_Ve = Ve_hat - Ve; 
e_Vn = Vn_hat - Vn;

Чтобы получить количественную оценку, дополнительно вычислим нормированные значения ошибок ( для положения и для скорости), приведённых к общему числу полученных значений:

# Нормированные ошибки измерений координат, м
n_xe_norm = round(norm(n_xe,1)/length(n_xe), digits = 3);
n_xn_norm = round(norm(n_xn,1)/length(n_xn), digits = 3);

# Нормированные ошибки оценок координат фильтром Калмана, м
e_xe_norm = round(norm(e_xe,1)/length(e_xe), digits = 3);
e_xn_norm = round(norm(e_xn,1)/length(e_xn), digits = 3);

# Нормированные ошибки оценок скорости фильтром Калмана, м/с
e_Ve_norm = round(norm(e_Ve,1)/length(e_Ve), digits = 3);
e_Vn_norm = round(norm(e_Vn,1)/length(e_Vn), digits = 3);

Построение сравнительных графиков ошибок определения позиционированния. В легенде указано нормированное значение.

#gr()      # Отключение интерактивности при построении графиков (легче для отрисовки)
plotlyjs() # Включение интерактивности (сложнее для отрисовки)
plot(
        plot(t_d, [n_xe e_xe], title = "Сравнительные графики ошибок позиционирования",
        label = ["Измерения (восток): $n_xe_norm" "Оценка (восток): $e_xe_norm"], 
        lw = 1.5, c = ["red" "green"], ylabel = "Восток, м"),
        plot(t_d, [n_xn e_xn],
        label = ["Измерения (север): $n_xn_norm" "Оценка (север): $e_xn_norm"], 
        lw = 1.5, c = ["black" "blue"], xlabel = "Время, с",
        ylabel = "Север, м"),
        layout = (2,1), legend=:right
)

Видно, что фильтр Калмана даёт улучшение в определении позиционирования примерно на

На графиках ниже показано сравнение оценки скорости с её истинным значением на примере восточной составляющей, а также ошибка оценки фильтра Калмана (значение ошибки в легенде нормированное).

#gr()      # Отключение интерактивности при построении графиков (легче для отрисовки)
plotlyjs() # Включение интерактивности (сложнее для отрисовки)
plot(
    layout = (2,1),
    plot(t_d, [Ve Ve_hat], title = "Сравнение оценки скорости",
    label = ["Действительная" "Фильтр Калмана"], lw = 1.5, c = ["blue" "green"],
    ylabel = "Скорость, м/с"),
    plot(t_d, e_Ve,
    label = "Ошибка: $e_Ve_norm", lw = 1.5, c = "red",
    xlabel = "Время, с", ylabel = "Ошибка фильтра, м/с",
    legend=:right)
)

По результатам моделирования можно сказать, что оценка скорости, сформированная фильтром Калмана, определяется корректно, о чём свидетельствует схожий с истинной скоростью график.
Отклонение оценки от действительного положения особенно сильно проявляется в моменты, когда автомобиль движется с высокой скоростью, что соответствует модели ковариационной матрицы .
На графике ошибки также видно два больших выброса вблизи моментов времени с и с.
В эти моменты автомобиль резко замедляется и совершает крутой поворот соответственно.
В связи с этим изменения скорости, оцененные с помощью фильтра, существенно отличаются от того, что происходит на самом деле.
Это обстоятельство и приводит к появлению пиков ошибки.
Однако через несколько шагов оценка "догоняет" истинное значение.

Заключение

С помощью алгоритма фильтрации Калмана была получена оценка положения и скорости автомобиля.
Особенностью данной модели было то, что шум процесса зависел от времени.
Результативность работы фильтра протестирована на различных манёврах автомобиля,
в то время как данные о его местоположении искажались случайно сгенерированным белым шумом.
Благодаря использованию фильтра Калмана, удалось повысить точность определения положения автомобиля и оценить его скорость, которая оказалась близкой к истинной.

Оценка параметров движения с помощью фильтра Калмана

Введение

Модель автомобиля

Модель дискретного фильтра Калмана

Моделирование

Заключение

Тип

Краткое описание

Связанные материалы

Теги

Категории

Языки

Форматы

Уровень

Статус

Опубликовано

Обновлено

Источник