Оценка параметров модели электропривода
Оценка параметров модели электропривода
Часто при моделировании возникает ситуация, когда законы, описывающие поведение объекта, известны, однако некоторые параметры, входящие в уравнения, остаются неопределёнными. В данном примере поэтапно рассмотрен процесс оценки неизвестных параметров модели электропривода на основе экспериментальных данных.
Подключение необходимых пакетов
Установим необходимые пакеты:
import Pkg
Pkg.add(["Interpolations","NLopt"])
Подключим необходимые пакеты:
using DataFrames, Plots,Interpolations, NLopt, MATLAB
Модель электропривода
Рассмотрим модель электропривода "motor_pe", схема которой представлена на рисунке ниже. Она состоит из контроллера, усилителя и электродвигателя с нагрузкой. Вход модели представляет собой сигнал управляющий положением нагрузки, выход - положение нагрузки.
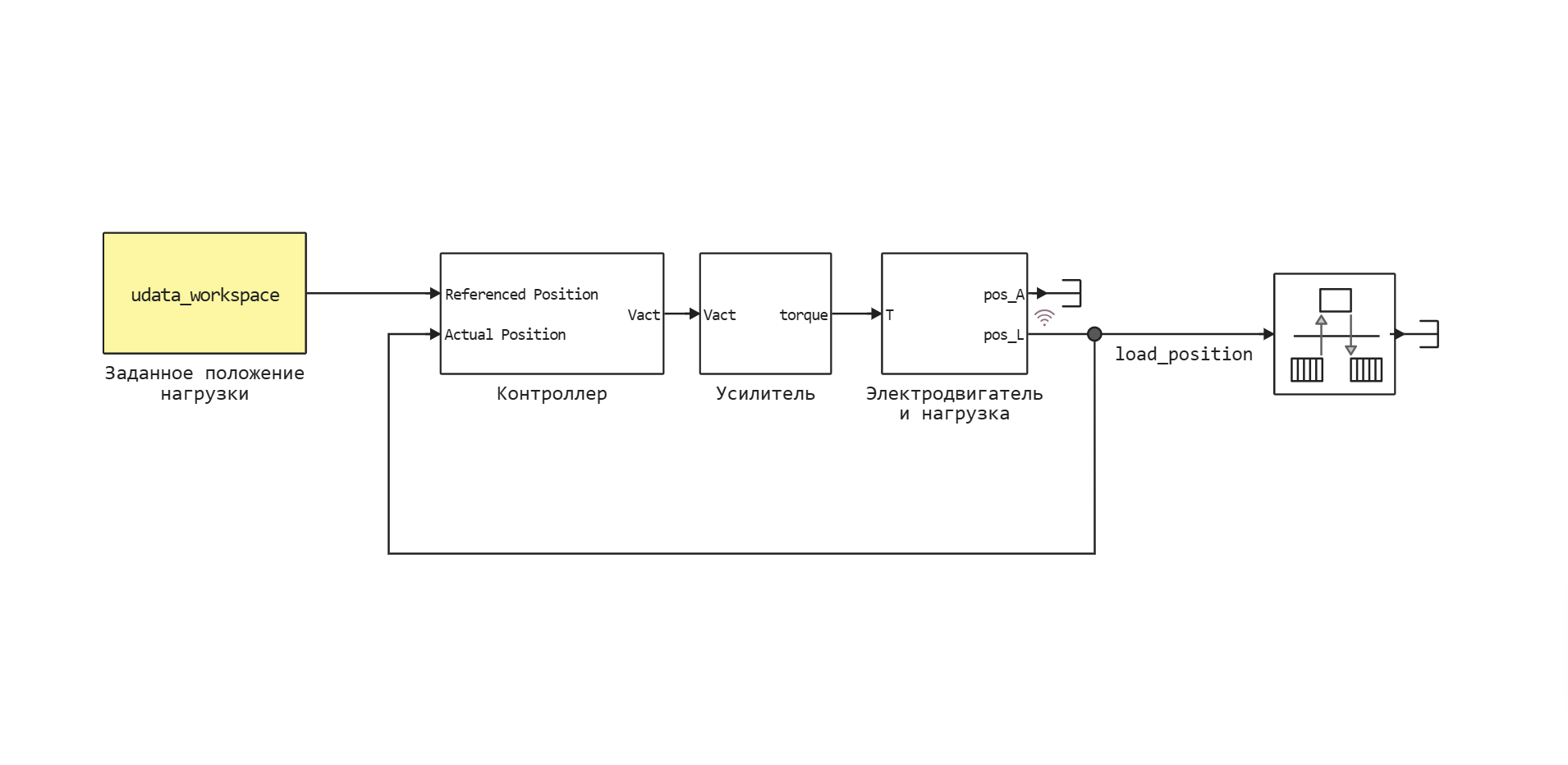
Для запуска симуляции модели нам необходимо указать значения следующих параметров:
J1- инерция ротора электродвигателя, ;J2- инерция нагрузки, ;k- жесткость гибкого вала, ;Km- постоянная электродвигателя, ;Ka- коэффициент усиления усилителя, ;b1- коэффициент демпфирования подшипников электродвигателя, ;b2- коэффициент демпфирования подшипников нагрузки, ;b12- коэффициент демпфирования гибкого вала, .
Некоторые из этих параметров известны и могут быть получены из технической документации или специализированных программ (например, систем автоматизированного проектирования — САПР), включая коэффициент усиления усилителя, моменты инерции нагрузки и ротора электродвигателя. Другие параметры могут быть определены с помощью прямых измерений, например, жесткость гибкого вала. Введём переменные, содержащие значения известных параметров:
J1 = 1.00e-6;
J2 = 1.35e-7;
k = 0.001;
Km = 16.4e-3;
Ka = 1.3/2.5;
Однако коэффициенты демпфирования не могут быть определены с помощью прямых измерений; их необходимо оценивать косвенно на основе экспериментальных данных о поведении всей системы. Поэтому зададим приближённые значения этих параметров:
b1 = 1e-5;
b2 = 1e-5;
b12 = 1e-5;
Загрузка результатов измерений
Загрузим значения измеренных сигналов из файла с экспериментальными данными "motor_data". В вектор tdata запишем значения моментов времени, в которые проводились измерения, в вектор udata — входной сигнал, представляющий заданное положение нагрузки, а в вектор ydata — выходной сигнал, соответствующий измеренному положению нагрузки:
data=read_matfile("$(@__DIR__)/motor_data.mat")
pa_input_voltage = jvector(data["pa_input_voltage"])
pa_output_voltage = jvector(data["pa_output_voltage"])
tdata = jvector(data["tdata"])
udata = jvector(data["udata"])
ydata = jvector(data["ydata"]);
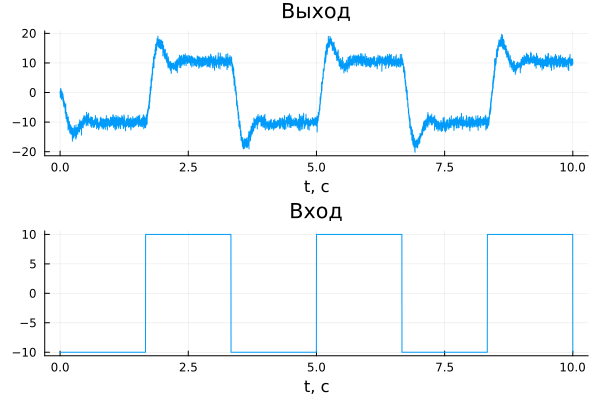
Построим графики измеренных сигналов:
gr()
input = plot(tdata, udata, title = "Вход", xlabel="t, c",legend=false)
output_measure = plot(tdata, ydata, title = "Выход", xlabel="t, c", legend=false)
plot(output_measure,input,layout = (2, 1))
Сравнение результатов моделирования и измерений
Для сравнения результатов моделирования и экспериментальных измерений необходимо подать входной сигнал в модель и зарегистрировать её выходные данные.
Создадим переменную типа WorkspaceArray для передачи входного сигнала udata в модель. Следует отметить, что в качестве значений времени для входного сигнала необходимо использовать вектор tdata.
udata_workspace = WorkspaceArray("udata_workspace", DataFrame(time = tdata, value = udata));
С помощью блока Заданное положение нагрузки (выделенного жёлтым на изображении ниже) входной сигнал udata_workspace передаётся на вход контроллера. Выходной сигнал load_position регистрируется при помощи логирования, его значения становятся доступны после завершения симуляции. Блок Заданное положение нагрузки и сигнал load_position соответствуют точкам сбора входных и выходных данных реальной системы.
.png)
Откроем модель "motor_pe", выполним её симуляцию, а затем построим график, отображающий результаты эксперимента и моделирования:
model = engee.load("motor_pe.engee")
logout = engee.run(model, verbose=false)
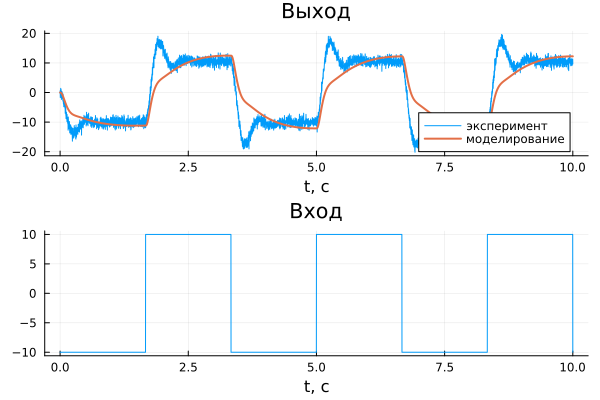
output = plot(tdata, ydata, title = "Выход", xlabel="t, c", label = "эксперимент", legend=true)
plot!(logout["load_position"].time, logout["load_position"].value, label = "моделирование", linewidth=2)
plot(output,input,layout = (2, 1))
Как видно из графика, динамика реальной системы и модели не совпадают. Это указывает на необходимость более точной настройки неизвестных параметров b1, b2, b12.
Оценка параметров при помощи оптимизации
Необходимо определить такие значения параметров b1, b2, b21, при которых выходной сигнал модели, записываемый блоком Положение нагрузки, максимально точно соответствует измеренным данным ydata.
Для этого будем минимизировать сумму квадратов ошибок между измеренным и смоделированным выходными сигналами. Ошибки вычисляются как разность между значениями измеренного выходного сигнала ydata и выходного сигнала модели load_position в моменты времени, заданные вектором tdata. Для минимизации суммы квадратов ошибок используем один из доступных алгоритмов оптимизации.
Важно отметить, что оцениваемые параметры b1, b2, b21 должны быть переменными (отображаться в рабочей области) и использоваться в модели. В данном примере они задействованы в блоке motor_pe/Электродвигатель и нагрузка/State-Space.
Маски работают только в Редакторе кода, поэтому приводим скриншот интерфейса, который станет вам доступен после открытия файла motor_pe.ngscript.
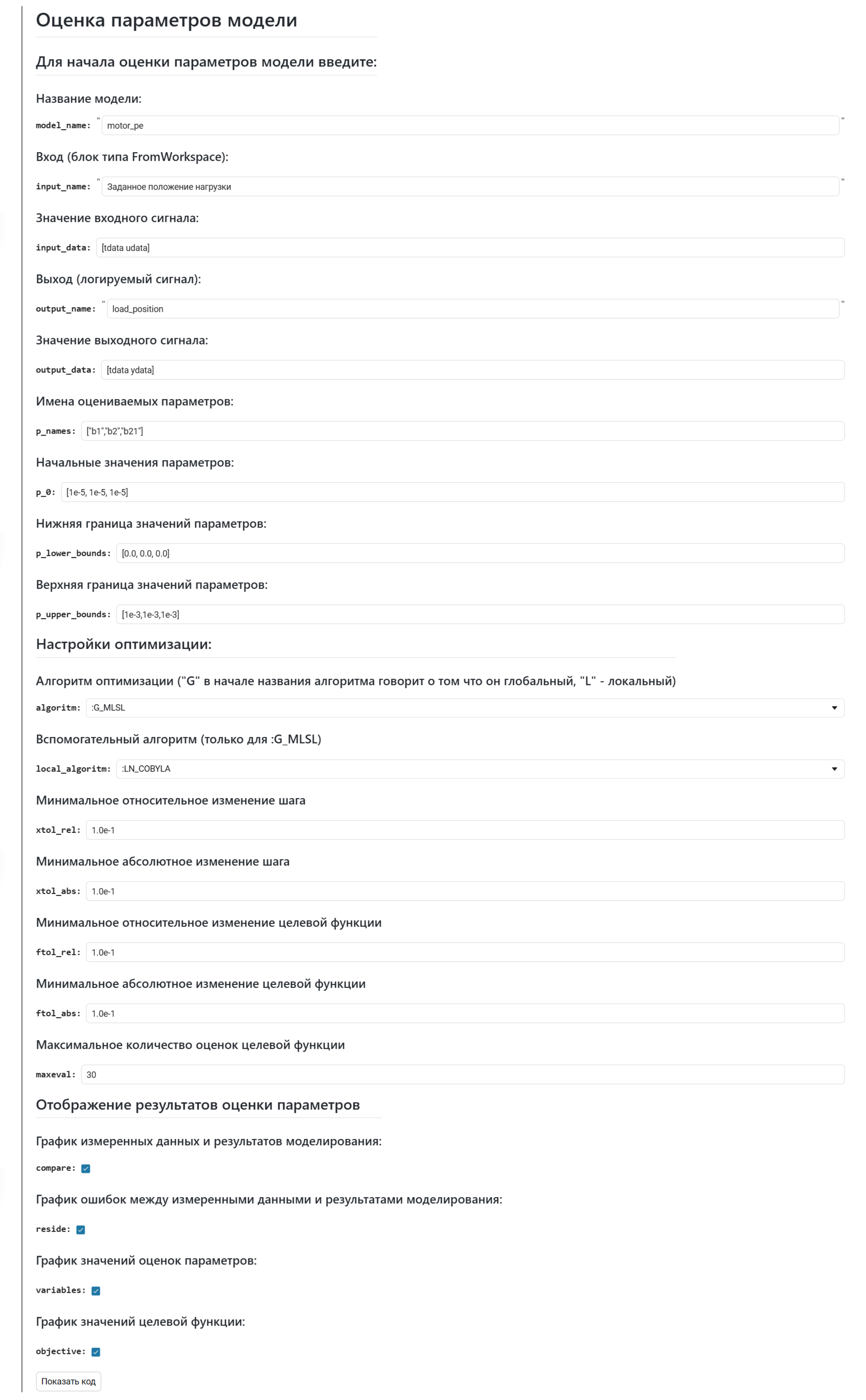
После выполнения необходимого количества итераций были получены следующие значения оцениваемых параметров:
b1= 2.9731e-6 — коэффициент демпфирования подшипников электродвигателя;b2= 9.1799e-23 — коэффициент демпфирования подшипников нагрузки;b12= 7.439e-6 — коэффициент демпфирования гибкого вала.
Визуальное сравнение результатов моделирования и эксперимента показывает, что достигнуто достаточно точное совпадение динамики модели с поведением реальной системы. Также можно построить дополнительные графики, выбрав соответствующие параметры, что позволит провести более детальный анализ результатов.
Качество оценки параметров зависит от следующих факторов:
- точности начальных значений параметров;
- наложенных ограничений на значения параметров;
- настроек алгоритма оптимизации;
- количества оцениваемых параметров.
Результаты
В данном примере рассмотрена возможность оценки неизвестных параметров, входящих в уравнения модели электропривода, на основе экспериментальных данных. Построен график сравнения результатов моделирования и эксперимента, который демонстрирует их совпадение, подтверждая корректность найденных значений параметров.