Моделируем первый искусственный спутник Земли

В этом проекте мы построим наземную трасу спутника ПС-1, запущенного 4 октября 1957.

Подготовка и запуск

Подготовимся к работе: откроем карту контуров побережий и зададим для нее желательную проекцию.

Pkg.add(["SatelliteToolbox", "Shapefile", "Proj"])

Мы заранее загрузили карту с репозитория Natural Earth. Более обширные сведения для работы с картами вы найдете здесь.

using Shapefile, Downloads, Proj

shp_path = joinpath(@__DIR__, "map", "ne_110m_coastline.shp");
table = Shapefile.Table(shp_path);

trans = Proj.Transformation("+proj=longlat", "+proj=robin +lon_0=0 +x_0=0 +y_0=0");

Теперь запустим модель. У нас получится несколько векторов состояния

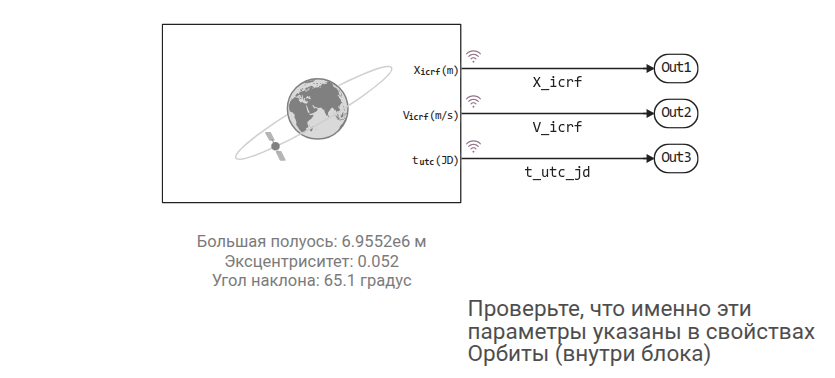
engee.open("sputnik_model.engee") # Закомментируйте, если модель уже открыта
data = engee.run("sputnik_model")

X_icrf = collect(data["X_icrf"]).value;
V_icrf = collect(data["V_icrf"]).value;
t_utc_jd = collect(data["t_utc_jd"]).value;

df = DataFrame( time = data["X_icrf"].time, t_utc_jd = t_utc_jd, X_icrf = X_icrf, V_icrf = V_icrf);

Мы собрали векторы в объект DataFrame, теперь наполним его дополнительными параметрами.

Перевод координат в другие системы

Для вывода графиков обычно координаты интересно перевести в геоцентрическую и геодезическую систему. Учтём следующие соображения:

для нашего проекта система ICRF почти идентична системе GCRF (ECI), погрешности будут порядка одного метра
наблюдатель будет располагаться в Москве
топоцентрические координаты строятся по эллипсоиду WGS84

using DataFrames
using SatelliteToolbox
using LinearAlgebra

# Где расположен наблюдатель
OBS_LLA = [deg2rad(55.7558), deg2rad(37.6173), 0.2e3]
eop = fetch_iers_eop()

# Добавляем новые столбцы
df[!, :lon] = zeros(length(df[!, :time]))
df[!, :lat] = zeros(length(df[!, :time])) 
df[!, :alt] = zeros(length(df[!, :time]))
df[!, :az] = zeros(length(df[!, :time]))
df[!, :el] = zeros(length(df[!, :time]))
df[!, :range] = zeros(length(df[!, :time]))

# Параметры Земли для преобразования координат наблюдателя
a = 6378137.0
lat_obs, lon_obs, alt_obs = OBS_LLA
x_obs = (a + alt_obs) * cos(lat_obs) * cos(lon_obs)
y_obs = (a + alt_obs) * cos(lat_obs) * sin(lon_obs)
z_obs = (a + alt_obs) * sin(lat_obs)

for i in 1:length(df[!, :time])
    # Преобразование ICRF → ITRF
    sv_icrf = OrbitStateVector(df[i, :t_utc_jd], df[i, :X_icrf], df[i, :V_icrf])
    sv_ecef = sv_eci_to_ecef(sv_icrf, GCRF(), ITRF(), df[i, :t_utc_jd], eop)
    
    # Геодезические координаты
    lat, lon, alt = ecef_to_geodetic(sv_ecef.r)
    df[i, :lon] = rad2deg(lon)
    df[i, :lat] = rad2deg(lat)
    df[i, :alt] = alt
    
    # Топоцентрические координаты
    Δr = sv_ecef.r - [x_obs, y_obs, z_obs]
    range_val = norm(Δr)
    
    # ENU координаты (Локальная система координат наблюдателя восток-север-верх)
    e = -sin(lon_obs)*Δr[1] + cos(lon_obs)*Δr[2]
    n = -sin(lat_obs)*cos(lon_obs)*Δr[1] - sin(lat_obs)*sin(lon_obs)*Δr[2] + cos(lat_obs)*Δr[3]
    u = cos(lat_obs)*cos(lon_obs)*Δr[1] + cos(lat_obs)*sin(lon_obs)*Δr[2] + sin(lat_obs)*Δr[3]
    
    az = atan(e, n) % (2π)
    el = atan(u, sqrt(e^2 + n^2))
    
    df[i, :az] = rad2deg(az)
    df[i, :el] = rad2deg(el)
    df[i, :range] = range_val
end

График земной трассы траектории космического аппарата

Полученные геодезические координаты можно просто вывести на график, но чтобы они были построены как линии, нужно сперва разделить каждый круг вокруг планеты на отдельные сегменты, чтобы не наблюдать лишних скачков на графике (между долготой 180 и -180).

ground_track_df = select(df, [:lon, :lat, :time])

# Наземная трасса орбиты
ground_track_lons = df.lon
ground_track_lats = df.lat

# Разбиваем на сегменты
jumps = findall(i -> abs(ground_track_lons[i+1] - ground_track_lons[i]) > 180, 1:length(ground_track_lons)-1)
segments = []
start_idx = 1

for jump_idx in jumps
    push!(segments, (ground_track_lons[start_idx:jump_idx], ground_track_lats[start_idx:jump_idx]))
    start_idx = jump_idx + 1
end

# Добавляем последний сегмент
push!(segments, (ground_track_lons[start_idx:end], ground_track_lats[start_idx:end]))

# Рисуем каждый сегмент отдельно
plot(title="Наземная трасса орбиты")
for (seg_lons, seg_lats) in segments
    xy_transf = trans.(seg_lons, seg_lats)
    xx,yy = getindex.(xy_transf, 1), getindex.(xy_transf, 2)
    plot!(xx, yy, legend=false, linecolor=:blue)
end
plot!()

for shape in table
    x = [point.x for point in shape.geometry.points]
    y = [point.y for point in shape.geometry.points]
    xy_transf = trans.(x, y)
    xx,yy = getindex.(xy_transf, 1), getindex.(xy_transf, 2)
    plot!(xx, yy, c=1, lw=0.5, fill=:lightblue)
end
plot!()

График спутниковой наблюдаемости с поверхности Земли

Для вывода графика наблюдаемости спутника из точки, где находится наблюдатель, мы рассчитали топоцентрические азимут и склонение. Отделим только те сегменты траектории, когда спутник находился над горизонтом.

# Точки над горизонтом
skyplot_mask = df.el .> 0

skyplot_az = df.az # df.az[skyplot_mask] # Эти данные уже можно вывести
skyplot_el = df.el # df.el[skyplot_mask] # но разделим их на сегменты

true_indices = findall(skyplot_mask)    # Разбиваем на непрерывные сегменты
gaps = findall(diff(true_indices) .> 1) # Находим разрывы в индексах
boundaries = vcat([1], gaps .+ 1, [length(true_indices) + 1]) # Границы сегментов

segments_az = Vector{Vector{eltype(skyplot_az)}}()
segments_el = Vector{Vector{eltype(skyplot_el)}}()
for i in 1:length(boundaries)-1
    start_idx = boundaries[i]
    end_idx = boundaries[i+1] - 1
    segment_indices = true_indices[start_idx:end_idx]
    push!(segments_az, skyplot_az[segment_indices])
    push!(segments_el, skyplot_el[segment_indices])
end

В отдельной ячейке выведем полусферу и нанесем на неё все сегменты, чтобы увидеть траекторию спутника такой, какой ее видели с поверхности Земли.

# Создаем полусферу
n = 30
u = range(0, 2π; length=n)
v = range(0, π/2; length=n)
x_sphere = cos.(u) .* sin.(v)'
y_sphere = sin.(u) .* sin.(v)'
z_sphere = ones(n) .* cos.(v)'

# Рисуем полусферу
surface(x_sphere, y_sphere, z_sphere, alpha=0.4, legend=false)
xlabel!("Восток"); ylabel!("Север"); zlabel!("Верх")

# Нанесение сегментов траектории
for (azimuths,elevations) in zip(segments_az, segments_el)
    # Преобразуем в декартовы координаты
    az_rad = deg2rad.(azimuths)
    el_rad = deg2rad.(elevations)
    x = cos.(el_rad) .* cos.(az_rad)
    y = cos.(el_rad) .* sin.(az_rad)
    z = sin.(el_rad)

    plot!(x, y, z, lw=4)
end
plot!(legend=false, title="Спутниковый график видимости (Москва)")

Мы видим, когда и как наблюдался спутник из точки в Москве. А поскольку вектор состояния спутника включает также и скорость, то мы можем посчитать допплеровское смещение и уточнить, как именно звучал его сигнал, зовущий нас к новым достижениям.

Заключение

Мы получили координаты спутника ПС-1 в течение 60 000 секунд наблюдения (настоящий спутник провёл на орбите около 8 миллионов секунд) и построили пару полезных графиков для интерпретации траектории этого космического аппарата.

Первый спутник

Моделируем первый искусственный спутник Земли

Подготовка и запуск

Перевод координат в другие системы

График земной трассы траектории космического аппарата

График спутниковой наблюдаемости с поверхности Земли

Заключение

Тип

Краткое описание

Связанные материалы

Теги

Категории

Языки

Форматы

Уровень

Статус

Опубликовано

Обновлено

Источник