Построение регрессионной модели в задачи предсказания затрат
Задача регрессии для предсказания медицинских затрат
Введение
В данном примере будет проведён разведочный анализ данных, включающий первичный осмотр структуры набора, изучение распределений признаков и целевой переменной, выявление пропусков, выбросов и дубликатов, а также анализ корреляций между переменными. На следующем этапе будут построены и обучены модели регрессии с целью прогнозирования целевой переменной и оценки качества их работы с помощью подходящих метрик. Дополнительно будет выполнен анализ важности признаков, что позволит определить, какие из них вносят наибольший вклад в предсказания модели и могут считаться наиболее значимыми для исследуемой задачи.
Необходимо установить библиотеки
Необходимо вручную прописать пути, где находится проект, чтобы перейти в рабочую директорию, а также установить необходимые зависимости
Перед началом работы импортируем все необходимые библиотеки
!pip install -r /user/Demo_public/biomedical/predictionmeddata/requirements.txt
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from scipy.stats import randint, uniform, loguniform
from sklearn.model_selection import train_test_split, RandomizedSearchCV, KFold
from sklearn.linear_model import Lasso
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
from sklearn.ensemble import RandomForestRegressor
from catboost import CatBoostRegressor
Считаем данные и посмотрим что они из себя представляют
df = pd.read_csv("insurance.csv")
df.head(10)
Проанализируем таблицу:
- age — возраст
- sex — пол
- bmi — индекс массы тела
- children — количество детей
- smoker — курит или нет
- region — регион проживания
- charges — медицинские расходы
На основе этой таблицы мы имеем признаки с 1 по 6 - входные данные в регрессионную модель, признак 7 - таргет, который нужно предсказать на основе признаков 1-6
EDA анализ
Проверим таблицу на наличие пропусков
df.info()
Пропусков нет. Видим в таблице 3 категориальных признака, которые впоследствии будут закодированы для обучения модели, остальные признаки числовые. Также видно, что отсутствуют пропуски.
df.describe()
Из статистики видно, что средний возраст людей 39 лет с отклонением в 14, то есть он находится в пределах от 25 до 53. Также видно, что присутствует bmi = 53 - это максимальное значение, что сильно превышает критический порог. Возможно, это выброс. Также видно, что половина людей имеет bmi больше 30,то есть большинство страдает начальными стадиями ожирения, а четверть клиентов имеет последнюю степень ожирения. Максимальные расходы составляет 63к условных единиц (у.е.), что сильно выбиваетс из картины (mean + 3sigma, mean -3sigma), возможно это наблюдение также является выбросом
Классические модели машинного обучения не могут работать с категориальными признаками, то есть с признаками, предскавляющие не числа. Их нужно закодировать в числа. Используем технику One Hot Encoding
df_encode = pd.get_dummies(df, columns=["sex", "region", "smoker"])
df_encode = df_encode.drop('sex_female', axis=1)
df_encode = df_encode.drop('smoker_no', axis=1)
df_encode.head()
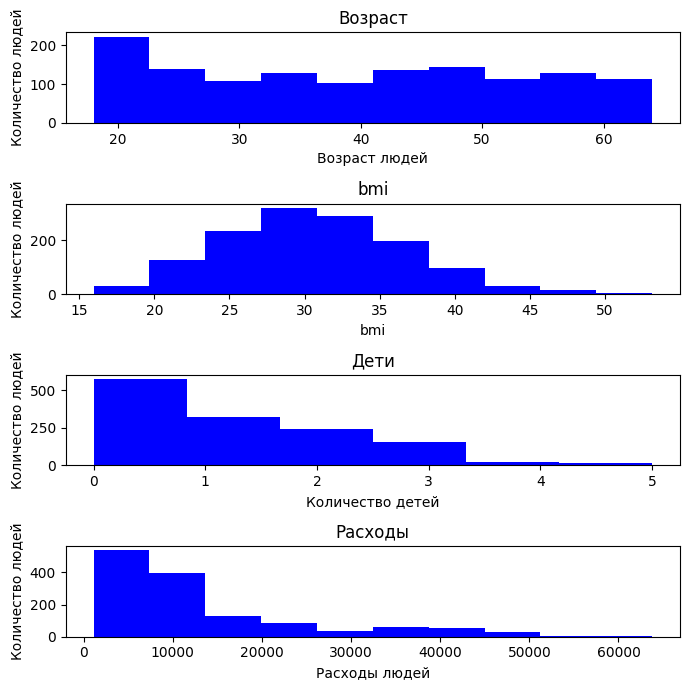
Для начала изучим распределение данных. Построим гистограмы для признаков
colors = ['blue', 'green', 'red', 'purple', 'orange']
fig, axes = plt.subplots(nrows=4, ncols=1,figsize=(7, 7))
axes = axes.flatten()
axes[0].hist(df["age"], bins=10, color=colors[0])
axes[0].set_title('Возраст')
axes[0].set_xlabel("Возраст людей")
axes[0].set_ylabel("Количество людей")
axes[1].hist(df["bmi"], bins=10, color=colors[0])
axes[1].set_title('bmi')
axes[1].set_xlabel("bmi")
axes[1].set_ylabel("Количество людей")
axes[2].hist(df["children"], bins=6, color=colors[0])
axes[2].set_title('Дети')
axes[2].set_xlabel("Количество детей")
axes[2].set_ylabel("Количество людей")
axes[3].hist(df["charges"], bins=10, color=colors[0])
axes[3].set_title('Расходы')
axes[3].set_xlabel("Расходы людей")
axes[3].set_ylabel("Количество людей")
plt.subplots_adjust(hspace=0.6)
plt.tight_layout()
По возрасту видно, что в выборке данные распределены достаточно равномерно: есть и молодые (от 18 лет), и пожилые (до 64 лет), но заметных перекосов нет.
Распределение BMI имеет вид нормального распределения, похоже на колокол, смещённый вправо. Большинство людей находятся в диапазоне от 25 до 35, что соответствует избыточному весу и ожирению. Есть клиенты с очень высоким BMI (>40).
По числу детей распределение резко скошено: большинство клиентов не имеют детей.
По расходам видно, что большая часть людей предпочитает тратить меньше 30к у.е.
Далее проведем анализ того, как тот или иной признак зависит друг от друга. Рассмотрим корреляцию признаков. Будем использовать корреляцию Спирмана, поскольку она не требует нормальности распределения
spearman_corr = df_encode.corr(method='spearman')
spearman_corr['charges'].sort_values(ascending=False)
Исходя из таблички выше, можно заключить вывод, что с расходами высокую корреляцию имеют факторы курения, возраста, то есть если человек курит, то у него больше расходов из-за необходимости трат на сигареты. Аналогично с возрастом. В зависимости от возраста человек имеет разные траты. Также можно понять, что количество детей не сильно влияет на расходы (можно увидеть, что большая часть наблюдаемых не имеет детей, поэтому корреляция с тратами маленькая), как и регион проживания, пол и bmi.
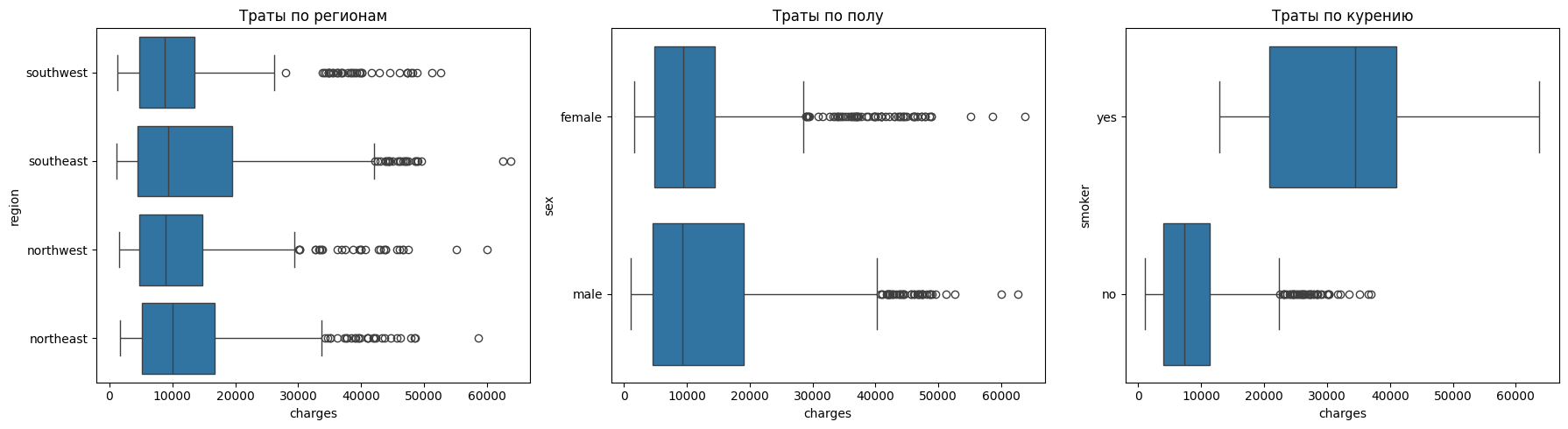
Посмотрим как категориальные признаки влияют на траты
fig, axes = plt.subplots(1, 3, figsize=(18, 5))
sns.boxplot(y="region", x="charges", data=df, ax=axes[0])
axes[0].set_title("Траты по регионам")
sns.boxplot(y="sex", x="charges", data=df, ax=axes[1])
axes[1].set_title("Траты по полу")
sns.boxplot(y="smoker", x="charges", data=df, ax=axes[2])
axes[2].set_title("Траты по курению")
plt.tight_layout()
plt.show()
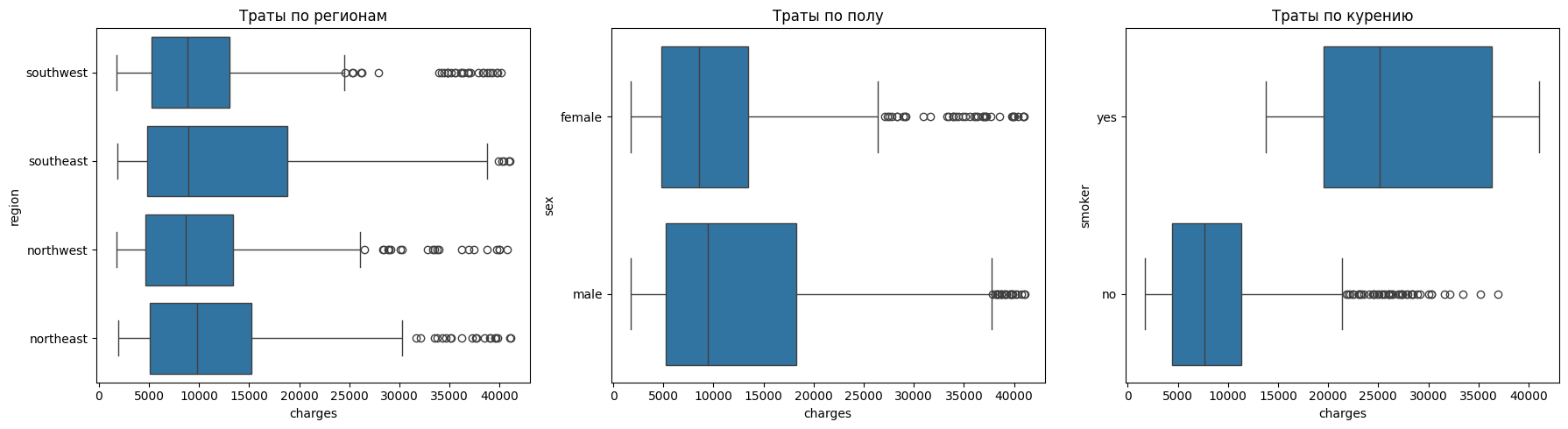
По регионам видно, что различия в расходах практически отсутствуют. Регионы имеют схожие распределения, а выбросы встречаются везде.
По полу также не наблюдается заметных различий.
С курением обратная ситуация. У некурящих расходы составляют менее 10 тысяч, а у курящих — около 35 тысяч. Разброс у курящих также сильно шире, что говорит о наличии большого числа случаев с крайне высокими затратами.
plt.figure(figsize=(8,5))
sns.scatterplot(x="age", y="charges", hue="smoker", data=df, alpha=0.6)
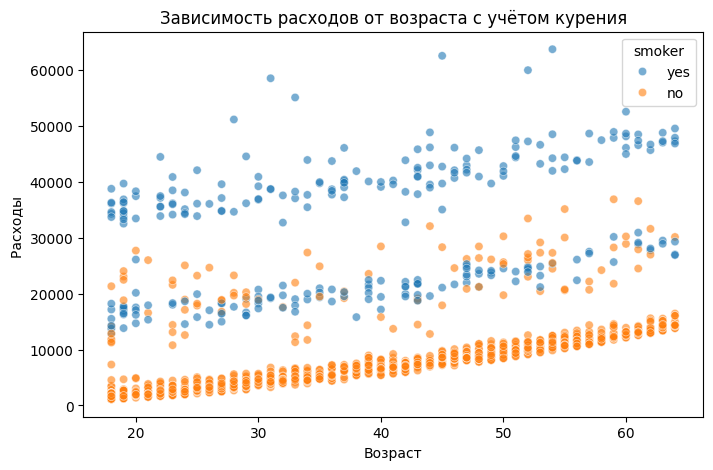
plt.title("Зависимость расходов от возраста с учётом курения")
plt.xlabel("Возраст")
plt.ylabel("Расходы ")
plt.show()
Можно увидеть, что расходы линейно растут с возрастом, то есть обслуживание возрастных людей более затратно. Также видно, что есть некий коэффициент, на который смещается зависимость расходов от возраста при наличии фактора курения
df['bmi_group'] = pd.cut(df['bmi'], bins=[0, 25, 30, 100],
labels=['Норма', 'Избыточный вес', 'Ожирение'])
g = sns.FacetGrid(df, col="smoker", hue="bmi_group", height=5)
g.map(sns.scatterplot, "age", "charges", alpha=0.6).add_legend()
plt.show()
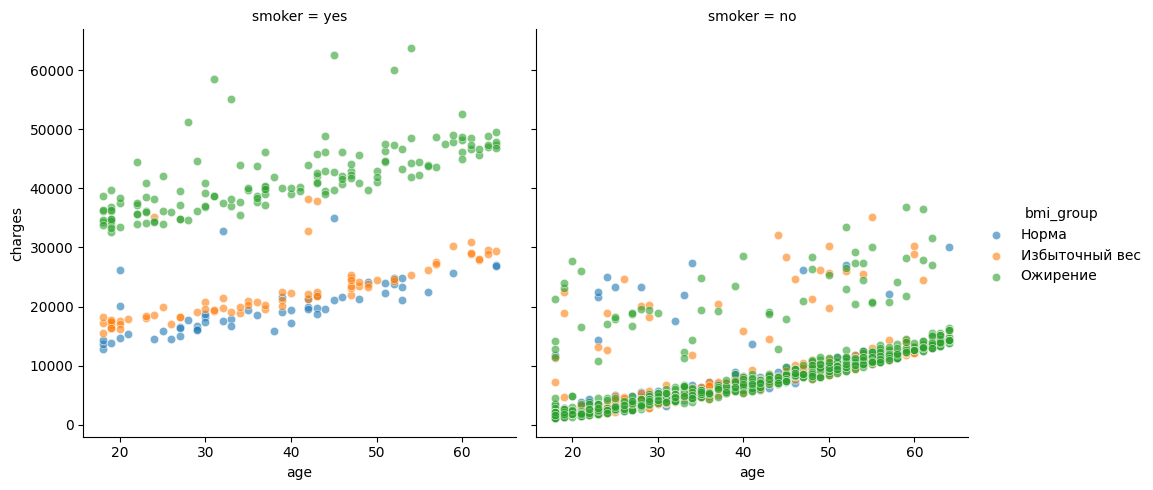
На графиках выше можно сделать следующие выводы:
У некурящих расходы растут с возрастом, но в целом остаются в умеренных пределах. Даже при ожирении затраты обычно не превышают 20–25 тысяч. Это говорит о том, что без фактора курения влияние веса выражено не так сильно.
У курящих людей чётко видно две линии: одна группа курильщиков тратит в среднем около 20 тысяч - люди с нормальным весом или избыточным весом, а другая группа стабильно выше — порядка 35–50 тысяч -это курильщики с ожирением.
Проверим, влияют ли на расходы людей количество детей
plt.figure(figsize=(8,5))
sns.barplot(x="children", y="charges", data=df, estimator=lambda x: x.mean())
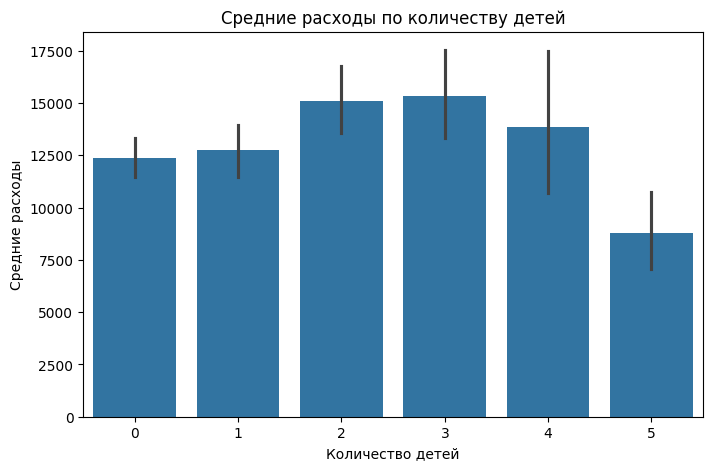
plt.title("Средние расходы по количеству детей")
plt.xlabel("Количество детей")
plt.ylabel("Средние расходы")
plt.show()
Количество детей практически не влияет на медицинские расходы. Единственное, когда 2-3 ребенка, расходы чуть выше среднего
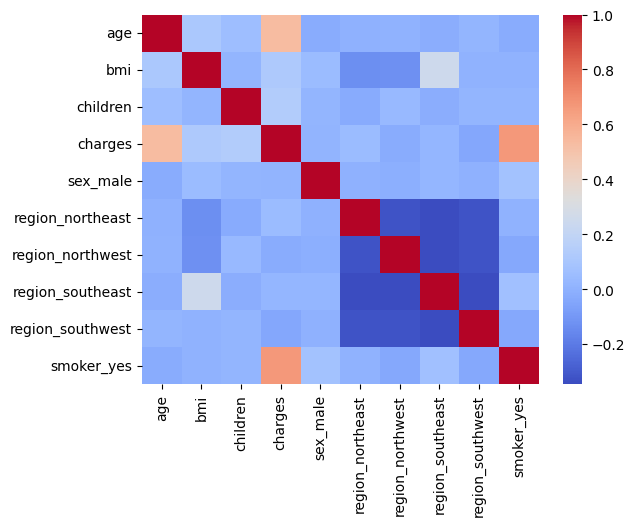
Посмотрим общую картину корреляции признаков, нарисуем тепловую карту, что предскавлена ниже
sns.heatmap(df_encode.corr(method='spearman'), cmap="coolwarm", annot=False)
Если смотреть корреляцию по признакам, то также можно заметить, что есть небольшая связь между bmi и регионом проживания, а в частности регионом "Southwest". То есть у них имеется больше выраженная связь линейная
Обучение модели
Список моделей, которые мы оценим при обучении
- Linear Regression
- Random Forest
- CatBoost Regressor
Liner Regression (Lasso)
Создадим таблицу, куда будем записывать результаты обучения моделей
Result_model = pd.DataFrame(columns=["Model", "MAE", "RMSE", "R2"])
Для линейных моделей важно правильно работать с категориальными переменными, именно поэтому мы им закодировали с помощью One Hot Encoding
В коде ниже y - наша целевая переменная - затраты, а X - признаки, на которых будет обучаться модель. Общий набор данных делим на тестовый и тренировочный, чтобы после обучения модели оценить ее обобщающую способность на тех данных, с которыми она еще не встречалась
Метрики, по которым мы будем оценивать обученную модель:
- MAE - средняя абсолютная ошибка, будет показывать на сколько в среднем ошибается модель
- RMSE - среднеквадратичная ошибка, большие ошибки штрафуются сильнее
- R2 - коэффициент детерминации, показывает, насколько модель объясняет» данные
X = df_encode.drop("charges", axis=1)
y = df_encode["charges"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
Первой моделью будет Lasso. В коде ниже идет обучение, расчет метрик а также вывод тех признаков, которые модель считает менее информативными. Однако даже такие признаки могут носить существенный вклад.
lasso = Lasso(alpha=0.5)
lasso.fit(X_train, y_train)
y_pred_lasso = lasso.predict(X_test)
mae_lasso = mean_absolute_error(y_test, y_pred_lasso)
rmse_lasso = np.sqrt(mean_squared_error(y_test, y_pred_lasso))
r2_lasso = r2_score(y_test, y_pred_lasso)
print("Lasso Regression")
print("MAE:", mae_lasso)
print("RMSE:", rmse_lasso)
print("R²:", r2_lasso)
coef_lasso = pd.DataFrame({
"Feature": X.columns,
"Coefficient": lasso.coef_
}).sort_values(by="Coefficient", ascending=False)
print("Коэффициенты Lasso:")
print(coef_lasso)
Добавим значения метрик в табличку
row = pd.DataFrame({
"Model": ["Lasso"],
"MAE": [mae_lasso],
"RMSE": [rmse_lasso],
"R2": [r2_lasso]
})
Result_model = pd.concat([Result_model, row])
Random Forest
Следующей моделью будет случайный лес. Принцип такой же, обучаем, тестируем, смотрим важность признаков
rf = RandomForestRegressor(
n_estimators=100,
max_depth=4,
min_samples_split = 20,
min_samples_leaf = 20
)
rf.fit(X_train, y_train)
y_pred_rf = rf.predict(X_test)
mae_rf = mean_absolute_error(y_test, y_pred_rf)
rmse_rf = np.sqrt(mean_squared_error(y_test, y_pred_rf))
r2_rf = r2_score(y_test, y_pred_rf)
print("Random Forest")
print("MAE:", mae_rf)
print("RMSE:", rmse_rf)
print("R²:", r2_rf)
importances = pd.DataFrame({
"Feature": X.columns,
"Importance": rf.feature_importances_
}).sort_values(by="Importance", ascending=False)
print("\nВажность признаков:")
print(importances)
Добавим метрики в табличку
row = pd.DataFrame({
"Model": ["Random Forest"],
"MAE": [mae_rf],
"RMSE": [rmse_rf],
"R2": [r2_rf]
})
Result_model = pd.concat([Result_model, row])
Видно, что у модели случайного леса метрики намного лучше, чем у линейной модели.
CatBoost Regressor
Следующая модель - модель градиентного бустинга из пакета CatBosot. Пройдем тот же пайплайн, что и с моделями выше.
cat_features = ["smoker", "sex", "region"]
feature_cols = [c for c in df.columns if c not in ["charges"]]
cat = CatBoostRegressor(
iterations=1000,
depth=6,
learning_rate=0.01,
verbose=100, random_state=42
)
X = df[feature_cols]
y = df["charges"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
cat.fit(X_train, y_train, cat_features=cat_features, eval_set=(X_test, y_test), verbose=100)
y_pred_cat = cat.predict(X_test)
mae_cat1 = mean_absolute_error(y_test, y_pred_cat)
rmse_cat1 = np.sqrt(mean_squared_error(y_test, y_pred_cat))
r2_cat1 = r2_score(y_test, y_pred_cat)
feature_importance = cat.get_feature_importance(prettified=True)
print(feature_importance)
print("CatBoost")
print("MAE:", mae_cat1)
print("RMSE:", rmse_cat1)
print("R²:", r2_cat1)
Добавим метрики в табличку
row = pd.DataFrame({
"Model": ["CatBoostRegressor 1ver"],
"MAE": [mae_cat1],
"RMSE": [rmse_cat1],
"R2": [r2_cat1]
})
Result_model = pd.concat([Result_model, row])
Далее попробуем для модели градиентного бустинга подобрать более оптимальные гиперпараметры. Сдесь будут учитываться сразу три метрики, которые я описывал выше
Поиск гиперпараметров будем осуществлять случайным поиском, выбрав те параметры и их диапозоны, с которыми работает модель
scoring = {
"mae": "neg_mean_absolute_error",
"rmse": "neg_root_mean_squared_error",
"r2": "r2",
}
cat_base = CatBoostRegressor(
verbose=False,
random_state=42,
task_type="GPU",
devices="0"
)
param_distributions = {
"iterations": randint(300, 1000),
"depth": randint(4, 8),
"learning_rate": loguniform(1e-3, 3e-1),
"l2_leaf_reg": loguniform(1e-2, 1e2),
"bagging_temperature": uniform(0.0, 1.0),
"random_strength": loguniform(1e-3, 10),
"grow_policy": ["SymmetricTree", "Depthwise"],
"border_count": randint(32, 128),
"leaf_estimation_iterations": randint(1, 3)
}
rs = RandomizedSearchCV(
estimator=cat_base,
param_distributions=param_distributions,
n_iter=20,
scoring=scoring,
cv=KFold(n_splits=5, shuffle=True, random_state=42),
n_jobs=1,
random_state=42,
refit=False
)
rs.fit(X_train, y_train, cat_features=cat_features)
Далее найдем среди всех метрик лучший результат. В нашем случае коэффициент детерминации показал в целом лучшием по всем метрикам цифры
cv = rs.cv_results_
best_idx = np.argmax(cv["mean_test_r2"])
best_params = cv["params"][best_idx]
print("Лучшая конфигурация по r2:", best_params)
На полученных гиперпараметрах обучим модель
best_cat = CatBoostRegressor(
verbose=False, random_state=42, task_type="GPU", devices="0", **best_params
)
best_cat.fit(X_train, y_train, cat_features=cat_features)
y_pred = best_cat.predict(X_test)
mae = mean_absolute_error(y_test, y_pred)
rmse = np.sqrt(mean_squared_error(y_test, y_pred))
r2 = r2_score(y_test, y_pred)
print("MAE:", mae)
print("RMSE:", rmse)
print("R²:", r2)
fi = best_cat.get_feature_importance(prettified=True)
print(fi)
И также в табличку внесем расчитанные метрики
row = pd.DataFrame({
"Model": ["CatBoostRegressor 2ver"],
"MAE": [mae],
"RMSE": [rmse],
"R2": [r2]
})
Result_model = pd.concat([Result_model, row])
Проведем Feature Engeneering, создав новые признаки из имеющихся. В нашем случае разделим возраст на декады, поделим людей, имеющих детей, на группы, а также поделим на классы индекс bmi (то есть по интервалам)
df = pd.read_csv("insurance.csv")
df["age_decade"] = (df["age"] // 10).astype(int).astype("category")
df["children_bucket"] = pd.cut(df["children"], [-1,0,2,99], labels=["0","1-2","3+"])
df["obesity_class"] = pd.cut(df["bmi"],
[0,18.5,25,30,35,40,1e3], labels=["Under","Normal","Over","Ob1","Ob2", "Ob3"])
После проведем такой же пайплайн по обучению базовой модели
cat_features = ["smoker", "sex", "region", "obesity_class", "age_decade", "children_bucket"]
feature_cols = [c for c in df.columns if c not in ["charges"]]
cat = CatBoostRegressor(
iterations=2000,
depth=6,
learning_rate=0.01,
verbose=100, random_state=42
)
X = df[feature_cols]
y = df["charges"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
cat.fit(X_train, y_train, cat_features=cat_features, eval_set=(X_test, y_test), verbose=100)
y_pred_cat = cat.predict(X_test)
mae_cat = mean_absolute_error(y_test, y_pred_cat)
rmse_cat = np.sqrt(mean_squared_error(y_test, y_pred_cat))
r2_cat = r2_score(y_test, y_pred_cat)
feature_importance = cat.get_feature_importance(prettified=True)
print(feature_importance)
print("CatBoost")
print("MAE:", mae_cat)
print("RMSE:", rmse_cat)
print("R²:", r2_cat)
Ну и запишем метрики в табличку
row = pd.DataFrame({
"Model": ["CatBoostRegressor 3ver"],
"MAE": [mae_cat],
"RMSE": [rmse_cat],
"R2": [r2_cat]
})
Result_model = pd.concat([Result_model, row])
Далее проверим, как на датасете с новыми признаками поведет себя модель с лучшими параметрами, которые были найдены через случайный поиск
cat_features = ["smoker", "sex", "region", "obesity_class", "age_decade", "children_bucket"]
feature_cols = [c for c in df.columns if c not in ["charges"]]
best_cat = CatBoostRegressor(
verbose=False, random_state=42, task_type="GPU", devices="0", **best_params
)
X = df[feature_cols]
y = df["charges"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.15, random_state=42)
cat.fit(X_train, y_train, cat_features=cat_features, eval_set=(X_test, y_test), verbose=100)
y_pred_cat = cat.predict(X_test)
mae_cat = mean_absolute_error(y_test, y_pred_cat)
rmse_cat = np.sqrt(mean_squared_error(y_test, y_pred_cat))
r2_cat = r2_score(y_test, y_pred_cat)
feature_importance = cat.get_feature_importance(prettified=True)
print(feature_importance)
print("CatBoost")
print("MAE:", mae_cat)
print("RMSE:", rmse_cat)
print("R²:", r2_cat)
Как обычно записываем результаты в табличку
row = pd.DataFrame({
"Model": ["CatBoostRegressor 4ver"],
"MAE": [mae_cat],
"RMSE": [rmse_cat],
"R2": [r2_cat]
})
Result_model = pd.concat([Result_model, row])
Проведем эксперимент. Найдем выбросы и удалим их. Проверим, как поведет себя модель градиентного бустина
В данном случае мы удаляем данные, которые могут сильно искажать картину для модели и портить метрики, конечно.
Мы удаляем данные следующие:
0.05-квантиль — значение, ниже которого находятся 5% наблюдений.
0.95-квантиль — значение, выше которого находятся 5% наблюдений.
df = pd.read_csv("insurance.csv")
numeric_cols = df.select_dtypes(include=[np.number]).columns
low = df[numeric_cols].quantile(0.05)
high = df[numeric_cols].quantile(0.95)
df_no_outliers = df[~((df[numeric_cols] < low) | (df[numeric_cols] > high)).any(axis=1)]
Выведем информацию о датасете
df_no_outliers.info()
Видно, что удалилось порядка 300 экземляров данных. В данном случае мы теряем процентов 20 от всей информации, что не рекомендуется делать, но мы смотрим, как эти 20 процентов влияют на конечное предсказание модели
Построим боксплоты, которые строились в пункте выше, и оценим распределение данных
fig, axes = plt.subplots(1, 3, figsize=(18, 5))
sns.boxplot(y="region", x="charges", data=df_no_outliers, ax=axes[0])
axes[0].set_title("Траты по регионам")
sns.boxplot(y="sex", x="charges", data=df_no_outliers, ax=axes[1])
axes[1].set_title("Траты по полу")
sns.boxplot(y="smoker", x="charges", data=df_no_outliers, ax=axes[2])
axes[2].set_title("Траты по курению")
plt.tight_layout()
plt.show()
Видно, что выбросов чуть поменьше стало
Дальше на обрезанном датасете обучим модель градиентного бустинга и проверим метрики
cat_features = ["smoker", "sex", "region"]
feature_cols = [c for c in df.columns if c not in ["charges"]]
cat = CatBoostRegressor(
iterations=2700,
depth=9,
learning_rate=0.002,
verbose=100, random_state=42
)
X = df_no_outliers[feature_cols]
y = df_no_outliers["charges"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.15, random_state=42)
cat.fit(X_train, y_train, cat_features=cat_features, eval_set=(X_test, y_test), verbose=100)
y_pred_cat = cat.predict(X_test)
mae_cat = mean_absolute_error(y_test, y_pred_cat)
rmse_cat = np.sqrt(mean_squared_error(y_test, y_pred_cat))
r2_cat = r2_score(y_test, y_pred_cat)
feature_importance = cat.get_feature_importance(prettified=True)
print(feature_importance)
print("CatBoost")
print("MAE:", mae_cat)
print("RMSE:", rmse_cat)
print("R²:", r2_cat)
Запишем все в табличку
row = pd.DataFrame({
"Model": ["CatBoostRegressor 5ver"],
"MAE": [mae_cat],
"RMSE": [rmse_cat],
"R2": [r2_cat]
})
Result_model = pd.concat([Result_model, row], ignore_index=True)
Оценим результаты
Result_model
Из представленной таблицы видно, что наилучшие значения метрики R² показали модели Random Forest и градиентного бустинга (5-я версия). Однако стоит учитывать, что модель градиентного бустинга обучалась на преобразованных данных, где были удалены потенциальные выбросы (пусть даже такие клиенты действительно могут встречаться в выборке). В то же время модель Random Forest демонстрирует более высокое значение R² на исходном датасете, но её показатели RMSE и MAE хуже. Это указывает на присутствие в исходных данных наблюдений с затратами, значительно превышающими средний уровень. Так, при среднем значении порядка 20 тыс. у.е. встречаются случаи с расходами около 60 тыс. у.е. Подобные экстремальные значения увеличивают ошибки в абсолютных метриках у Random Forest. В отличие от него, модель градиентного бустинга, обученная без выбросов, показала более низкие ошибки MAE и RMSE.
Таким образом, среди всех обучаемых моделей наилучшей будем считать ту, которая имеет суммарно самые низкие показатели метрик.
В нашем случае это градиентный бустинг 5 версии
Какие факторы сильнее всего влияют на target?
Оценим важность признаков 2 спосабами:
- Важность, основанная на EDA
- Важность, полученная с помомью моделей
Важность, основанная на EDA
Рассмотрим все признаки отдельно
Курение (smoker)
Самый значимый фактор. Коэффициент корреляции между курением и расходами составляет 0.66, что указывает на сильную связь.
На графиках видно, что у курящих расходы значительно выше, чем у некурящих.
Диаграмма рассеяния также показывает, что даже при одинаковом возрасте и BMI курящие имеют расходы в разы выше.
Курение резко увеличивает риски для здоровья (болезни сердца, легких, онкология), что ведет к росту затрат.
Возраст (age)
На втором месте по силе влияния идет возраст (корреляция 0.53).
Графики показывают — чем старше человек, тем выше расходы.
Особенно заметно это для курильщиков: с возрастом их расходы растут, вид немного напоминает экспоненциальную зависимость.
Причина — с возрастом увеличивается вероятность хронических заболеваний и обращений за медицинской помощью.
Наличие детей (children)
Корреляция слабая (0.13), но всё же положительная.
Семьи с 2–3 детьми имеют в среднем более высокие расходы, чем бездетные или с одним ребенком.
Однако при 5 детях средние расходы снижаются — это может быть связано с особенностями выборки.
Причина — наличие детей увеличивает затраты на здоровье
Индекс массы тела (BMI)
Корреляция с расходами слабая (0.11), но в сочетании с другими факторами BMI играет роль.
В графиках видно, что люди с ожирением имеют более высокие расходы, особенно если они курят.
При этом само по себе ожирение без курения не всегда приводит к резкому росту затрат.
Причина — ожирение связано с рисками диабета, сердечно-сосудистых заболеваний, но эти эффекты усиливаются при других факторах риска.
Пол и регион (sex, region)
По полу и региону заметного влияния нет.
Корреляции близки к нулю.
Распределение расходов почти одинаково для мужчин и женщин, а также для разных регионов.
Причина — страховые тарифы и медицина не зависят от региона проживания или пола в данной выборке.
Важность, полученная с помомью моделей
Аналогичную картину важности мы увидим, если посмотрим на то, какие признаки имеют больший, а какие малых вес после обучения модели.
Так, например, для модели Случайный лес, коэффициенты важности признаков после обучения:
-
smoker_yes 0.700647 -
bmi 0.175183 -
age 0.115571
Видно, что во время EDA также было установлено, что именно эти признаки имеют высокую важность
Так, например, для двух моделей градиентного бустинга важны были именно эти признаки, просто с разными коэффициентами:
-
smoker -
bmi -
age
Тем самым, можно однозначно сделать вывод, что самыми значимыми признаками являются фактор курения, индекс bmi, и возраст.
Заключение
В примере был проведён разведочный анализ данных, обучены модели регрессии и определены наиболее значимые признаки, влияющие на целевую переменную.