Представления (views) как способ повысить быстродействие
Представления (views) как способ повышения производительности кода
В данном скрипте рассматривается применение представлений - механизма, позволяющего обращаться к элементам массива, не создавая их копий.
Будут затронуты темы:
- отличие копии среза (slicing) от представления (view)
- использование макросов
@viewи@viewsи их различия.
Для того чтобы проверить эффективность использования представлений - подключим библиотеки BenchmarkTools
import Pkg; Pkg.add("BenchmarkTools")
Проблема копирования
Когда мы используем синтаксис b = a[1:5], то b становится копией первых пяти элементов a, а не "связывается по адресу" с элементами a.
a = collect(1:10)
b = a[1:5] # [1, 2, 3, 4, 5]
println(pointer(a))
println(pointer(b))
b .= 0 # [0, 0, 0, 0, 0]
a' # как видим, матрица не поменялась, что и логично
Чтобы изменить наш исходный вектор, мы вынуждены делать лишнее действие:
a[1:5] .= b[1:5]
a'
Функция view
Представления как раз позволяют использовать привычный синтаксис, но создавать не копии, а обращаться напрямую к "ячейкам памяти" массивов.
Для этого можно использовать функцию view
a = collect(1:10000)
# '÷' не то же, что и '/' (÷ = div())
view_of_a = view(a,1:length(a)÷2) # end здесь не сработает
view_of_a .= 0
a
pointer(view_of_a) == pointer(a)
Давайте же убедимся в том, что использование представлений позволяет нам избегать выделения лишней памяти под копии, используя @allocated, показывающий количество выделенных байт.
println(@allocated (subarray_of_a = a[1:end÷2]))
println(@allocated (view_of_a = view(a,1:length(a)÷2)))
@view
Но использование функции view не соответствует вышесказанному утверждению о "привычном интерфейсе", поскольку мы не могли использовать, например, ключевое слово end.
Для решения этой проблемы можно использовать макрос @view:
a = repeat(1:10,inner=3)
b = @view a[end-3:end]
b .= 0
a'
Но может возникнуть вопрос: зачем нужны лишние переменные, когда можно просто сделать
a = repeat(1:10,inner=3)
a[end-3,3] .= 0
Ответом на это можно сформулировать так:
Представления нужны как объединение эффективного использования ресурсов и сохранения читаемости кода.
Пусть есть задача вывести и посчитать сумму тройки (triplet) элементов.
for i in 0:(length(a)÷3-1)
println("sum of $(a[3i+1:3i+3]) -> $(sum(a[3i+1:3i+3]))")
end
Видно, что есть повторяющиеся элементы, а также легко ошибиться в одной из индексаций.
for i in 0:(length(a)÷3-1)
triplet = a[3i+1:3i+3]
println("sum of $triplet -> $(sum(triplet))")
end
Помимо этого, мы можем видеть, что функция, использующая представления - будет выделять намного меньше памяти и работать существенно быстрее.
Для этого мы будем использовать макрос @btime, показывающий время выполнения функции и выделяемую при этом память, прогоняя функцию несколько раз и усредняя значения.
(Из функций убрали вывод в консоль, чтобы не засорять консоль во время множественного вызова функций)
using BenchmarkTools
function tripletssum_subarray(v)
for i in 0:(length(v)÷3-1)
triplet = v[3i+1:3i+3]
end
end
function tripletssum_view(v)
for i in 0:(length(v)÷3-1)
triplet = @view v[3i+1:3i+3]
end
end
a = repeat(1:10000,inner=3)
println(@btime tripletssum_subarray(a))
println(@btime tripletssum_view(a))
@views
Рассмотрим следующий пример
Pkg.add("LinearAlgebra")
using LinearAlgebra
@btime dot( a[1:end÷2], a[end÷2+1:end])
И, казалось бы, мы знаем, как можно улучшить этот код:
try
# ОСНОВНОЙ КОД
#------------------------------------------------------
@btime dot(@view a[1:end÷2], @view a[end÷2+1:end])
#------------------------------------------------------
# ОБРАБОТКА ИСКЛЮЧЕНИЯ
catch e
io = IOBuffer();
showerror(io, e)
error_msg = String(take!(io))
end
В ошибке говорится, что мы неправильно используем макрос @view.
Хотя вроде бы наше выражение a[1:end÷2] соответствует выражению A[...].
Проблема заключатеся в том, что мы неправильно использовали макрос.
Для того чтобы исправить эту ситуацию - поместим вектора, к которым хотим применить представление, в скобки:
@btime dot(@view(a[1:end÷2]) ,@view(a[end÷2+1:end]))
Но чтобы для каждого среза (slicing) не писать @view мы можем использовать макрос @views
@btime @views dot((a[1:end÷2]), (a[end÷2+1:end]))
@viewsможно вставить перед определением функции, чтобы срезы внутри неё происходили с использованием представлений.
@views function tripletssum_views(v)
for i in 0:(length(v)÷3-1)
triplet = v[3i+1:3i+3]
end
end
a = repeat(1:10000,inner=3)
println(@btime tripletssum_views(a))
В каких случаях применять представления?
Представления стоит применять там, где:
- это повышает читабельность
- это влияет на производительность
- вы понимаете, в чём различие работы с копией и с оригиналом
a = rand(1000)
println(@allocated sum(a))
println(@allocated sum(a[1:end]))
println(@allocated sum(copy(a[1:end])))
println(@allocated sum(@view a[1:end]))
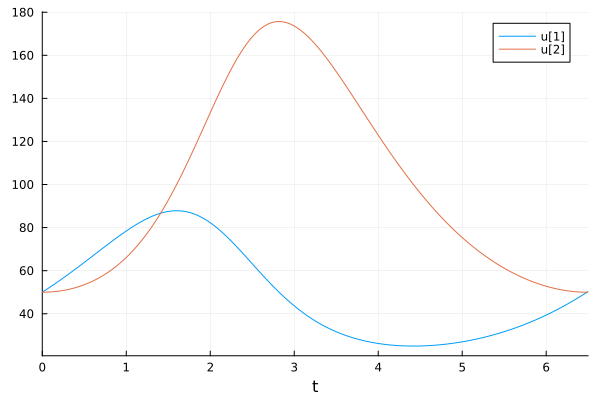
Рассмотрим пример решения уравнения Лотки-Вольтерра
import Pkg; Pkg.add(["OrdinaryDiffEq","Plots"])
using OrdinaryDiffEq
using Plots
gr()
function lotka(du, u, p, t)
du[1] = p[1] * u[1] - p[2] * u[1] * u[2]
du[2] = p[4] * u[1] * u[2] - p[3] * u[2]
end
α = 1; β = 0.01; γ = 1; δ = 0.02;
p = [α, β, γ, δ]
tspan = (0.0, 6.5)
u0 = [50; 50]
prob = ODEProblem(lotka, u0, tspan, p)
sol = solve(prob,saveat=0.001)
При отрисовке графиков будут использоваться зависимости переменных от времени и .
plot(sol)
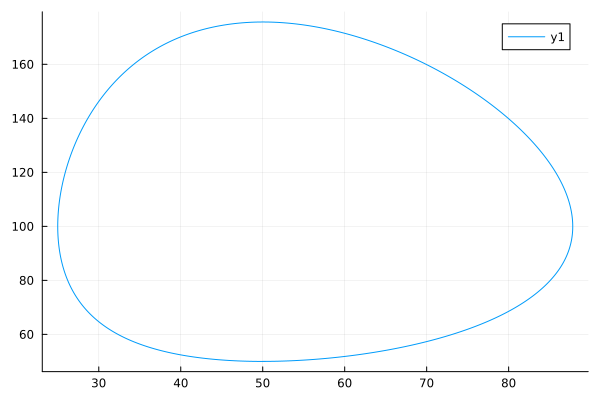
Но если мы захотим отрисовать зависимость , то мы вынуждены будем использовать срезы sol[1,:] и sol[2,:]. Что как раз напоминает нам нашу вышеупомянутую проблему.
@btime plot(sol[1,:],sol[2,:])
Которую теперь мы можем решить, используя представления:
@btime @views plot(sol[1,:],sol[2,:])
Выводы
Познакомившись с понятием представлений, были рассмотрены практические способы повышения производительности работы функций, не требующих никаких значительных изменений в код.