Система связи QPSK с адаптивным выравниванием

Модель представленная в этом примере демонстрирует практическую систему цифровой связи с модуляцией QPSK, которая борется с реальными проблемами беспроводных каналов: частотными смещениями, многолучевыми замираниями и шумами. Основная цель — показать эффективность адаптивного выравнивания канала с использованием RLS-фильтра для компенсации искажений.

Полный тракт передачи данных:

Генерация битов → Модуляция → Формирование импульса
Прохождение через реалистичный канал связи
Прием → Выравнивание → Демодуляция → Оценка ошибок

Ключевые эффекты канала:

Фазовое и частотное смещение (доплер до 10 Гц + фиксированный сдвиг 120°)
Многолучевое распространение (два пути с разными задержками и затуханиями)
Аддитивный белый гауссовский шум (SNR = 30 дБ)

Структура кадра

Обучающая последовательность (30 символов) — используется для "обучения" адаптивного фильтра
Полезные данные (50 символов) — реальная информация
Такая структура имитирует практические системы связи (Wi-Fi, LTE), где периодически передаются пилот-сигналы

Двухэтапная обработка

Кадр → [Обучающая часть] → RLS-фильтр (обучение) → [Данные] → FIR-фильтр (применение весов)

Этап обучения: RLS-фильтр настраивает коэффициенты на известной обучающей последовательности
Этап работы: Настроенные веса используются в FIR-фильтре для выравнивания полезных данных

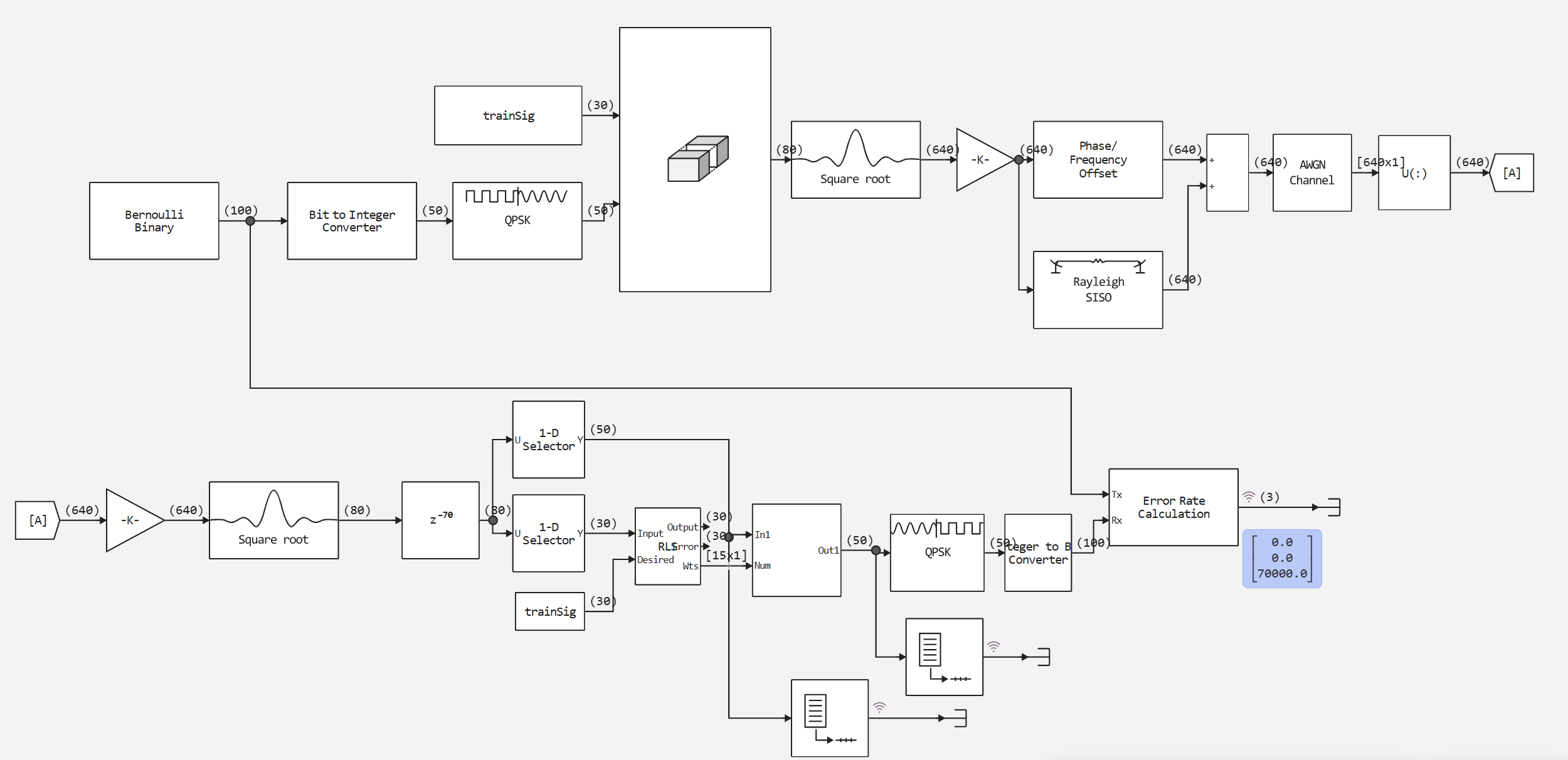
Что демонстрирует модель

Жизнеспособность QPSK в сложных условиях — даже при частотных смещениях и замираниях система сохраняет работоспособность
Эффективность адаптивного выравнивания — как правильно настроенный фильтр может "очистить" искаженный сигнал
Практический подход к синхронизации — использование обучающих последовательностей вместо идеальных предположений
Компромисс между эффективностью и накладными расходами — 30 символов обучения на 50 символов данных (37.5% накладных расходов)

Области применения

Образовательная демонстрация принципов цифровой связи
Тестирование алгоритмов выравнивания и компенсации
Оценка помехоустойчивости различных схем модуляции
Прототипирование решений для беспроводных систем

Теперь перейдём к инициализации и запуску модели, код представленный ниже инициализирует параметры системы связи QPSK с адаптивным выравниванием: задаёт скорость передачи 1 Мбит/с, структуру кадра (100 бит, включая 30 обучающих символов), параметры модуляции и формирующего фильтра, настраивает канал с частотным смещением до 10 Гц и двухлучевым замиранием, а также определяет параметры RLS-фильтра (15 весов и фактор забывания равный 0.95) и готовит обучающую последовательность для настройки выравнивателя.

bitRate = 1000000;
numBitsPerFrame = 100;
bitsPerSymbol = 2;
numTrainSyms = 30;
pulseDelay = 8;
oversampleFactor = 8;
rolloffFactor = 0.2;
modOrder = 2^bitsPerSymbol;
numDataSymsPerFrame = numBitsPerFrame / bitsPerSymbol;
numSymsPerFrame = numDataSymsPerFrame + numTrainSyms;

qpskmod = EngeeComms.QPSKBasebandModulator(PhaseOffset = pi/4);
trainSig = qpskmod(rand(0:modOrder-1,numTrainSyms));
maxDoppler = 10;

numEqWeights = 15;
refTap = 8;
lambda = 0.95;
snrdB = 30;


symbolPeriod = bitsPerSymbol/bitRate;
chanSamplePeriod = symbolPeriod/oversampleFactor * 50/80;

pathDelays = [0 chanSamplePeriod];
pathGains = [0 -6];

numDataSymsPerFrame = numBitsPerFrame / bitsPerSymbol;
numSymsPerFrame = numDataSymsPerFrame + numTrainSyms;

initEqWeights = complex(zeros(numEqWeights));
eqDelay = refTap - 1;
trimTrainSig = trainSig[1:end-eqDelay];

println("Скорость: $(bitRate/1e6) Мбит/с, Кадр: $(numBitsPerFrame) бит")
println("Структура: $(Int.(numDataSymsPerFrame)) данных + $(numTrainSyms) обучающих символов")
println("Канал: Доплер $(maxDoppler) Гц, 2 луча, SNR $(snrdB) дБ")
println("Выравниватель: RLS-фильтр $(numEqWeights) отсчётов, λ=$(lambda)")

Скорость: 1.0 Мбит/с, Кадр: 100 бит
Структура: 50 данных + 30 обучающих символов
Канал: Доплер 10 Гц, 2 луча, SNR 30 дБ
Выравниватель: RLS-фильтр 15 отсчётов, λ=0.95

function run_model( name_model)
    Path = (@__DIR__) * "/" * name_model * ".engee"
    if name_model in [m.name for m in engee.get_all_models()] # Проверка условия загрузки модели в ядро
        model = engee.open( name_model ) # Открыть модель
        model_output = engee.run( model, verbose=true ); # Запустить модель
    else
        model = engee.load( Path, force=true ) # Загрузить модель
        model_output = engee.run( model, verbose=true ); # Запустить модель
        engee.close( name_model, force=true ); # Закрыть модель
    end
    sleep(0.1)
    return model_output
end
run_model("qpsk_freqfade")

Building...
Progress 0%
Progress 2%
Progress 5%
Progress 6%
Progress 9%
Progress 14%
Progress 19%
Progress 24%
Progress 29%
Progress 33%
Progress 38%
Progress 43%
Progress 48%
Progress 53%
Progress 58%
Progress 63%
Progress 68%
Progress 73%
Progress 78%
Progress 83%
Progress 88%
Progress 93%
Progress 98%
Progress 100%
Progress 100%

SimulationResult(
    run_id => 2,
    "Error Rate Calculation.Output_1" => WorkspaceArray{Vector{Float64}}("qpsk_freqfade/Error Rate Calculation.Output_1")
,
    "Unbuffer-1.1" => WorkspaceArray{ComplexF64}("qpsk_freqfade/Unbuffer-1.1")
,
    "Unbuffer.1" => WorkspaceArray{ComplexF64}("qpsk_freqfade/Unbuffer.1")

)

WorkspaceArrays.plot_wa(WorkspaceArray{Vector{Float64}}("qpsk_freqfade/Error Rate Calculation.Output_1"))

Вывод

Анализируя график BER мы явно видим, что при наших параметрах канала, ошибка нулевая. Система показывает, что даже относительно простые методы адаптивной фильтрации (RLS + обучение по пилотам) позволяют эффективно бороться с серьезными искажениями в реальных каналах связи, делая высокоскоростную передачу данных возможной в неидеальных условиях. Модель иллюстрирует фундаментальный принцип цифровых коммуникаций: обработка на приемной стороне может компенсировать многие проблемы физического канала, превращая "грязный" аналоговый сигнал в чистые цифровые данные.

QPSK с адаптивным выравниванием

Система связи QPSK с адаптивным выравниванием

Вывод

Тип

Краткое описание

Связанные материалы

Теги

Категории

Языки

Форматы

Уровень

Статус

Опубликовано

Обновлено

Источник