Расчет стационарного теплового поля в детали
nkapyrinРасчет стационарного теплового поля в детали: Julia, Gmsh, Gridap, VTK и Makie¶
Применим цепочку инструментов, позволяющую в Engee спроектировать, параметризовать модель, нанести на нее расчетную сетку, построить задачу для решения методом конечных элементов и, в итоге, рассчитать теплопередачу в сложной детали.
Введение¶
Для задач, требующих точного решения уравнений в частных производных (например, теплопередачи или механики деформируемого тела), специализированные инструменты (вроде Gridap или FEniCS) дают более точные и гибкие результаты. Они позволяют работать с произвольными сетками и сложными граничными условиями, что критично для научных расчётов.
Pkg.add(["Gridap", "GridapGmsh", "CairoMakie", "WGLMakie", "WriteVTK", "ReadVTK", "GeometryBasics"])
Для этого примера мы используем библиотеку, установка которой автоматически добавляет в систему пакет Gmsh.
using GridapGmsh
Возьмем простой пример модели из репозитория этой библиотеки и слегка модифицируем его:
- область
boundary 1будет объединять внутреннюю поверхность более широкого отверстия (справа) - область
boundary 2- всю внутреннюю поверхность отверстия с выступом (слева)
Создание такой параметризованной модели можно выполнить в текстовом редакторе, например визуализируя результаты в https://gmsh.info/ или в одной из множества САПР для твердотельного моделирования, в том числе и с открытым кодом: OpenCASCADE, OpenSCAD и FreeCAD.
Загрузим пример в формате .geo (базовый формат для геометрии в Gmsh) и создадим сетку:
GridapGmsh.gmsh.initialize()
GridapGmsh.gmsh.clear()
GridapGmsh.gmsh.parser.parse("$(@__DIR__)/demo.geo");
GridapGmsh.gmsh.model.geo.synchronize();
GridapGmsh.gmsh.option.setNumber("Mesh.CharacteristicLengthMin", 0.01) # минимальный размер
GridapGmsh.gmsh.option.setNumber("Mesh.CharacteristicLengthMax", 0.05) # максимальный размер
GridapGmsh.gmsh.model.mesh.generate(3);
GridapGmsh.gmsh.write("demo.msh");
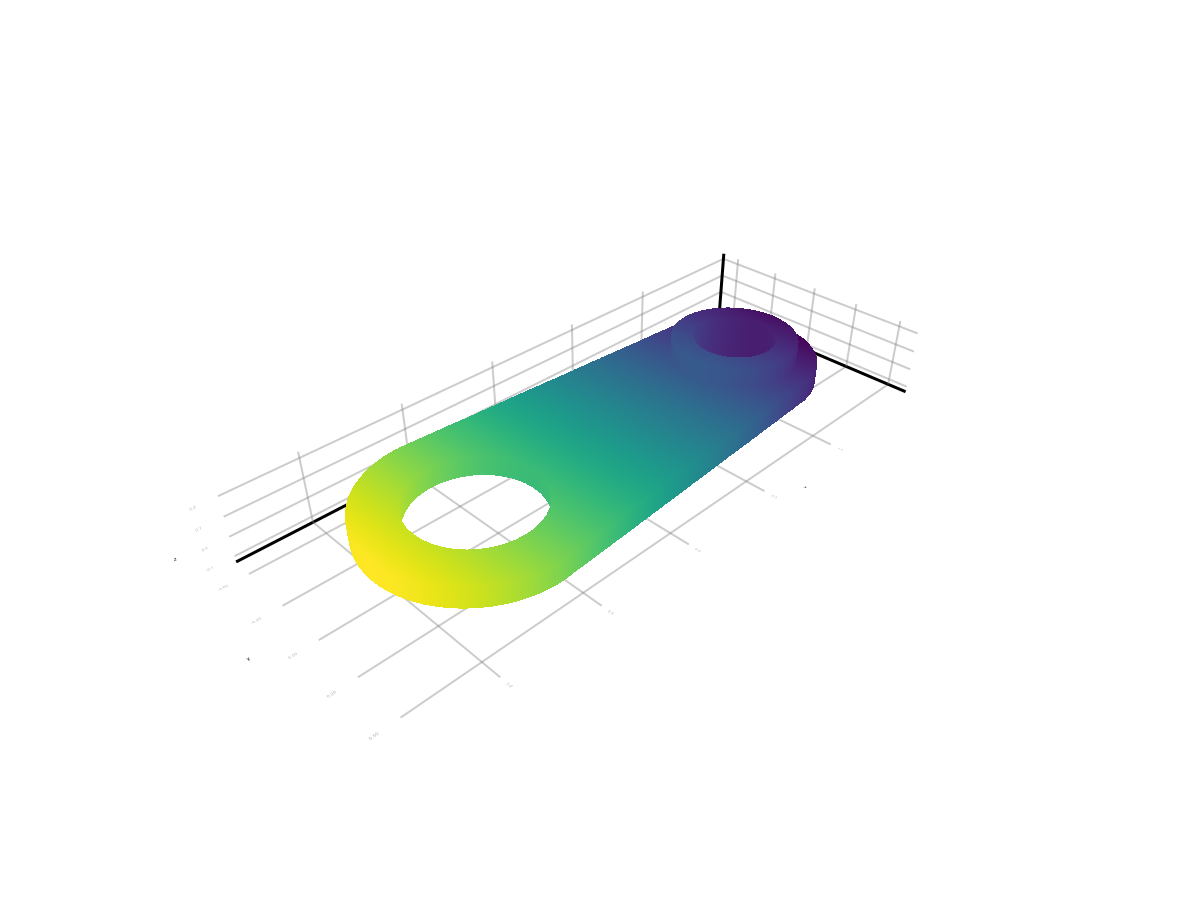
Выведем модель нашей детали, которая является набором тетраэдров (Makie не позволяет работать с тетраэдрами, поэтому мы вручную преобразовали их в треугольники). Расцветка графика соответствует координате точек по оси Х.
using Gridap, GridapGmsh, GeometryBasics
import CairoMakie: mesh, NoShading
# import WGLMakie: mesh, NoShading # На замену CairoMakie - для интерактивных графиков
model = GmshDiscreteModel("demo.msh");
grid = get_grid(get_triangulation(model))
points = reinterpret(reshape, Float64, grid.node_coordinates)
cells = hcat(grid.cell_node_ids...)
tetrahedra = [ (c[1], c[2], c[3], c[4]) for c in eachcol(cells) ]
all_faces = [ [TriangleFace{Int}(ta, tb, tc),TriangleFace{Int}(ta, tb, td),TriangleFace{Int}(ta, tc, td),TriangleFace{Int}(tb, tc, td)] for (ta, tb, tc, td) in tetrahedra ]
all_faces = reshape(reinterpret(Int, vcat(all_faces...)), 3, :)
colors = points[1,:]
mesh(points', all_faces', color=colors, shading=NoShading)
Постановка численной задачи¶
Мы используем код из базового примера для GridapGmsh, где решается уравнение Лапласа (Laplace's equation) с граничными условиями Дирихле (Dirichlet boundary conditions) в слабой (вариационной) формулировке методом конечных элементов (МКЭ).
Уравнение Лапласа и граничными условиями: Ищется функция $u(x)$, удовлетворяющая уравнению $\Delta u = 0$ в области $\Omega$ с граничными условиями $u = 0$ на $\Gamma_1$, $u = 1$ на $\Gamma_2$, где $\Omega$ — область, заданная сеткой
demo.msh, $\Gamma_1$ и $\Gamma_2$ — границы с тегами "boundary1" и "boundary2" соответственно.
Слабая форма (вариационная постановка задачи) - ключевой метод для современного МКЭ, он ослабляет требования по гладкости решения, также при нем граничные условия можно задать напрямую, не аппроксимируя их. И, конечно, это основной метод дискретизации задачи, позволяющий задать ее в базисных функциях и решить как линейную систему $Au = b$. Итак, наша задача в вариационной постановке преобразуется в $a(u, v) = \int_{\Omega} \nabla v \cdot \nabla u \, d\Omega = 0 \quad \forall v \in V_0$, где $\nabla$ — градиент, $\Omega$ — область интегрирования, $V_0$ — пробное пространство, обращающееся в ноль на границах.
Заметим, как близко описание, данное в коде ∫( ∇(v)⋅∇(u) )dΩ к уравнению Лапласа в вариационной постановке $a(u, v) = \int_{\Omega} \nabla v \cdot \nabla u \, d\Omega = 0 \quad \forall v \in V_0$.
using Gridap
model = GmshDiscreteModel("demo.msh"); # Загружаем геометрию сетки из файла *.msh
order = 1
reffe = ReferenceFE(lagrangian,Float64,order) # Линейные лагранжевы элементы 1-го порядка
V = TestFESpace(model,reffe,dirichlet_tags=["boundary1","boundary2"]) # Пробное пространство
U = TrialFESpace(V,[0,1]) # Определение пространства решений
# - на boundary1 значение решения u = 0
# - на boundary2 значение u = 1
Ω = Triangulation(model) # Триангуляция и мера интегрирования
dΩ = Measure(Ω,2*order)
a(u,v) = ∫( ∇(v)⋅∇(u) )dΩ # Слабая форма уравнения Лапласа
l(v) = 0 # Линейная форма (правая часть)
op = AffineFEOperator(a,l,U,V) # Собираем линейный оператор задачи
uh = solve(op) # Решение системы
writevtk(Ω,"demo",cellfields=["uh"=>uh]);
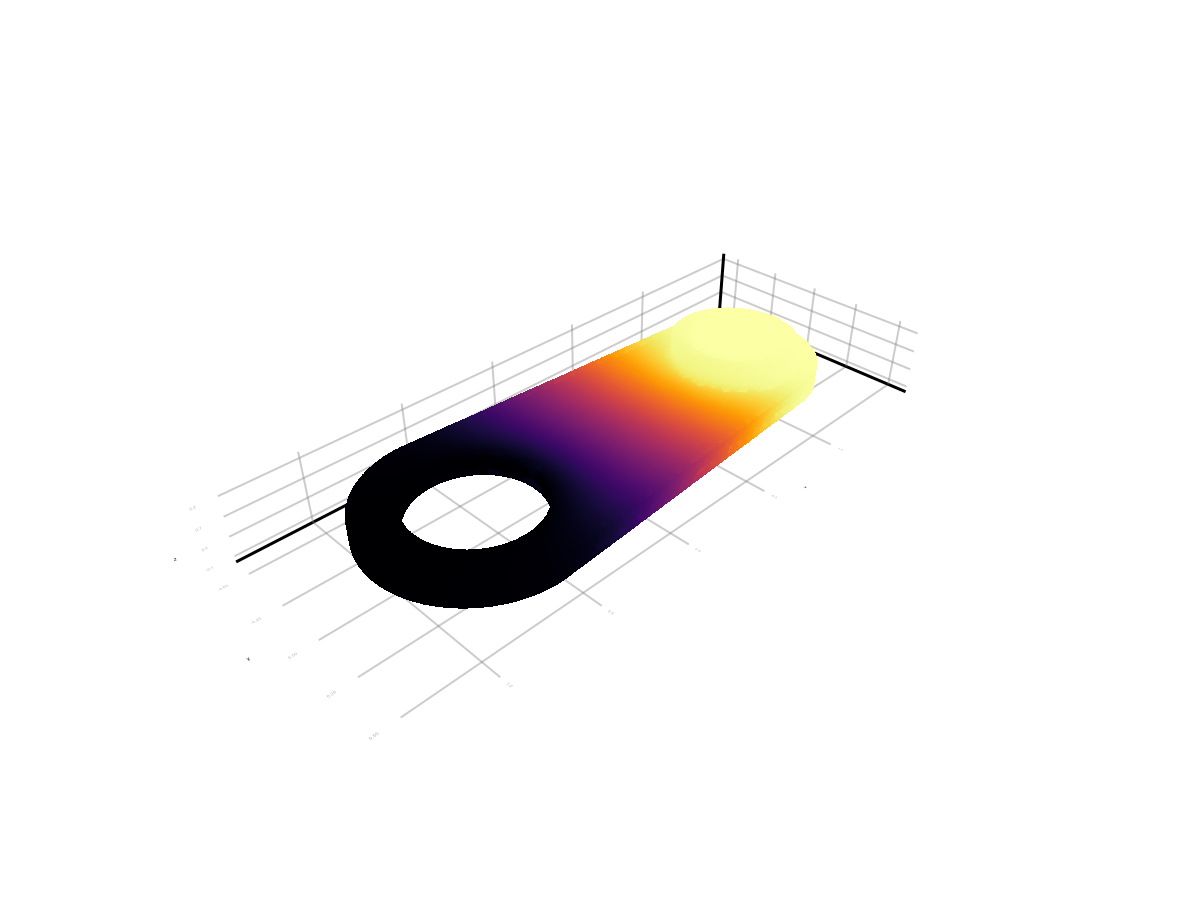
Мы пойдем немного дальше и кроме визуализации "на лету" покажем, как визуализировать расчет, сохраненный в VTK. Но, для начала, покажем только что поулченное решение:
using GeometryBasics
nodes = GridapGmsh.get_node_coordinates(Ω)
cell_node_ids = GridapGmsh.get_cell_node_ids(Ω)
uh_values = [uh(node) for node in nodes]
points = [Point3f(x...) for x in nodes]
faces = [TriangleFace(cell_node_ids[i][1], cell_node_ids[i][2], cell_node_ids[i][3]) for i in 1:length(cell_node_ids)]
mesh(points, faces, color=uh_values, colormap=:inferno, shading=NoShading)
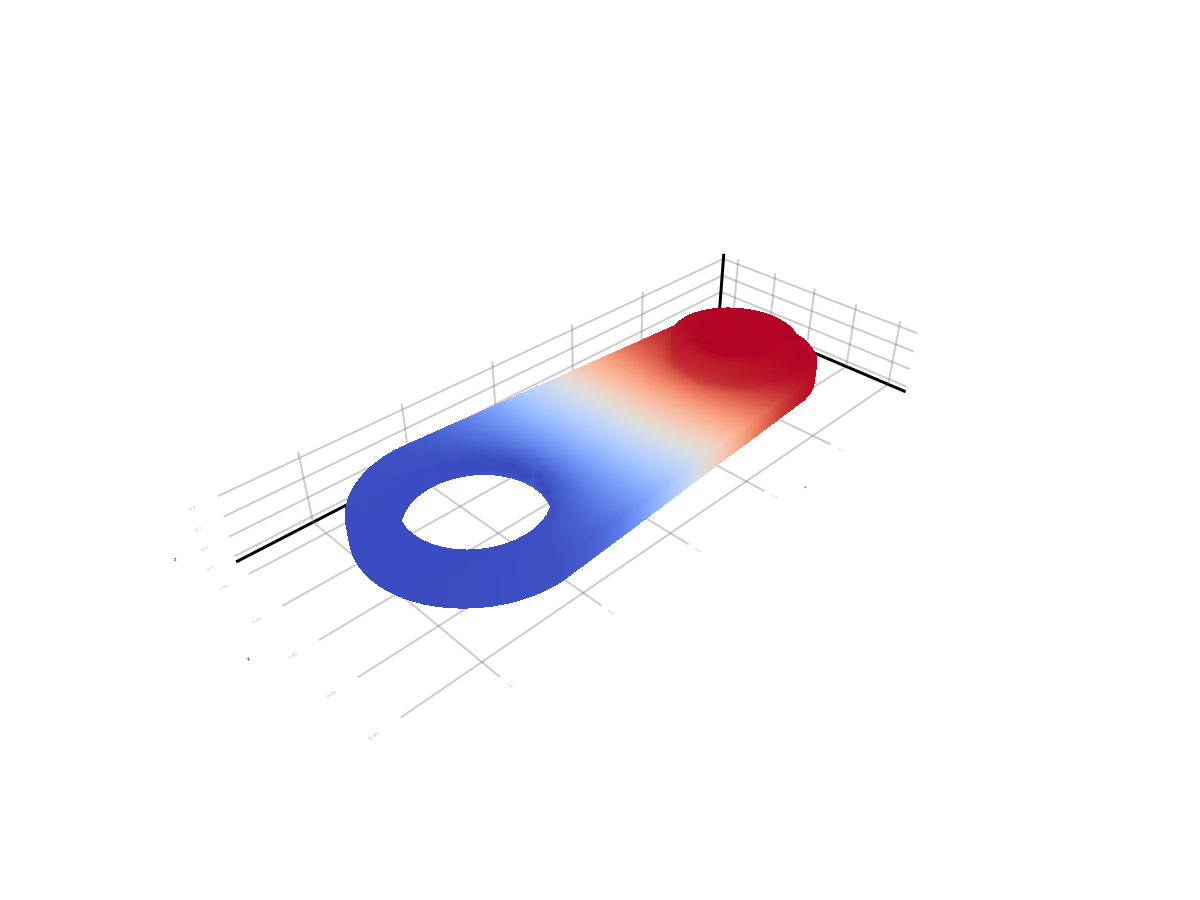
Визуализация решения из VTK файла¶
Для просмотра файлов VTK самое удобное решение - программа с открытым кодом ParaView. Но нам также ценно иметь интерактивные отчеты, полностью открывающиеся в Engee. Поэтому мы откроем этот файл в Julia и выведем решение прямо в этом скрипте.
Если запускать эту часть асинхронно с решением задачи (которое может занять много времени), нам потребуется подключить эти библиотеки:
using WriteVTK, ReadVTK
Они помогут нам прочитать VTK файл и вывести его на 3D графике. Для части функций есть дополнительные библиотеки, но мы пока обойдемся низкоуровневыми командами:
- создадим матрицу
pointsдля координат вершин - получим вектор
uh_values, где будут лежать значения поляuhнашего решения - разобьем тетраэдры
cellsна набор треугольниковall_faces
vtk = VTKFile("demo.vtu")
points = get_points(vtk)
uh_values = get_data(get_point_data(vtk)["uh"])
cells = get_cells(vtk)
# Разобьем массив cells.connectivity на тетраедры, а затем на треугольники
using GeometryBasics
all_faces = TriangleFace{Int}[]
offset = 1
while offset <= length(cells.connectivity)
ta, tb, tc, td = cells.connectivity[offset:offset+3]
push!(all_faces, TriangleFace(ta, tb, tc)) # грань 1
push!(all_faces, TriangleFace(ta, tb, td)) # грань 2
push!(all_faces, TriangleFace(ta, tc, td)) # грань 3
push!(all_faces, TriangleFace(tb, tc, td)) # грань 4
offset += 4
end
# CairoMakie не принимает последний треугольник в модели, временно используем [1:end-1]
mesh(points, all_faces[1:end-1], color=uh_values, colormap=:coolwarm, shading=NoShading)
Заключение¶
Мы реализовали решение уравнения Лапласа на тетраэдральной сетке, сохранили результаты в VTK-формате и визуализировали их — это основа для моделирования физических полей (тепловых, электрических, механических). Такой подход обеспечивает воспроизводимость, точность и готовность к масштабированию на реальные инженерные задачи, где требуются детальные расчёты, а не упрощённые системные аппроксимации.