Сообщество Engee
Engee Community
/
Примеры и проекты
/
Распространение ультракоротких импульсов в световоде SMF-28

Распространение ультракоротких импульсов в световоде SMF-28

Автор
avatar-daniil11daniil11
Соавторы
avatar-mon1kmon1k
Notebook

Распространение ультракоротких импульсов в волоконных световодах

Введение

Одной из задач при построении волоконных оптических систем, таких как волоконные лазеры или волоконно-оптические линии связи, является расчет динамики распространения ултракоротких импульсов (длительностью порядка пикосекунд) вдоль волоконного световода. Цель данного проекта состоит в решении данной задачи на примере распространения солитона в кварцевом световоде SMF-28, широко использующемся в телекоммуникациях, с использованием языка Julia.

Общее уравнение распространения

Для описания распространения ультракоротких импульсов в нелинейной среде с дисперсией, какой является волоконный световод, используется обобщенное нелинейное уравнение Шрёдингера, подробный вывод которого приведен в [1]. Здесь же представим его в готовом виде:

\begin{equation}
\begin{array}{r}
\frac{\partial A}{\partial z}+\frac{\alpha}{2} \mathrm{A}-\sum_{\mathrm{k} \geq 2} \frac{\beta_{\mathrm{k}}}{\mathrm{k}!} \frac{\partial^k \mathrm{~A}}{\partial T^k}= i \mathrm{\gamma}\left(1+\tau_{\text {shock }} i \frac{\partial}{\partial T}\right) \times \
{\left[\mathrm\mathrm{z}, \mathrm{~T} \int_{-\infty}^{\infty} \mathrm{R}\left(\mathrm{T}^{\prime}\right)\left|\mathrm{A}\left(\mathrm{z}, \mathrm{~T}-\mathrm{T}{\prime}\right)\right|2 \mathrm{dT}^{\prime}\right]},
\end{array}
\end

где — огибающая ультракороткого импульса, зависящая от координаты и вермени , ; — потери, ; — коэффициенты разложенной в ряд Тейлора постоянной распространения в окрестности центральной частоты , ; — мнимая единица; — нелинейный коэффициент, ; — функция нелинейного отклика среды, включающая комбинационное рассеяние и функцию отклика среды. Производная по времени в правой части уравнения учитывает дисперсию нелинейности, которая в большинстве случаев приводит к таким эффектам, как самообострение импульса и возникновение оптических ударных волн, характеризующиеся временем , измеряемым в секундах.

Для импульсов длительностью более 100 фс можно пренебречь членами дисперсии выше второго порядка, нулевым и первым, так как они не влияют на форму импульса. Также можно пренебречь комбинационным рассеянием, поглощением и образованием оптической ударной волны, считая их влияние малым. Принимая все эти условия, получим следующее уравнение:

\begin{equation}
\begin{array}{r}
i \frac{\partial A}{\partial z} - \frac{\text\beta_2}{2} \frac{\partial^2 A}{\partial T^2} + N^2 |A|^2 A = 0
\end{array}
\end

где — дисперсия групповых скоростей, ;
– знаковая функция. определяется, как: . Здесь – длительность импульса по уровню от максимальной интенсивности, которая соотносится с длительностью солитона на полувысоте следующим образом , пс; – пиковая мощность импульса, Вт;

Метод расчета

Уравнение выше является нелинейным дифференциальным уравнением с частными производными, для решения которого можно использовать разностные и псевдоспектральные методы. Обычно для моделирования используют псевдоспектральные методы, так как они на порядок быстрее благодаря использованию алгоритма быстрого Фурье-преобразования при той же точности расчета. Одним из наиболее широко используемых методов решения задачи распространения импульсов в нелинейной среде с дисперсией являются фурье-метод расщепления по физическим факторам.

Он заключается в применении операторов, отвечающих за дисперсию и нелинейность . Для численного интегрирования уравнение распространения удобно представить в следующем виде:
\begin{equation}
\frac{\partial A}{\partial z} = (\widehat{D} + \widehat{N})A.
\end

может быть записан в следующем виде:
\begin{equation}
\widehat{D} = -\frac{ i\beta_2}{ 2}\frac{\partial^2}{\partial T^2}
\end

может быть записан в следующем виде:
\begin{equation}
\widehat{N} = i\gamma|A|^2
\end

В общем случае дисперсия и нелинейность действуют вместе по всей длине световода.
Фурье-метод расщепления по физическим факторам позволяет получить приближенное решение, предполагая, что при распространении оптического поля на небольшое расстояние дисперсионные и нелинейные эффекты действуют независимо. Более конкретно, распространение от до осуществляется в два этапа. На первом этапе нелинейность действует сама по себе, и . На втором этапе дисперсия действует сама по себе, и .
В случае использования симметричного Фурье-метода решением через шаг h будет являться:

\begin{equation}
A(z+h, T) \approx \mathrm{exp}⁡\left(\frac{h}{2}\widehat{D} \right)\mathrm{exp}\left(\int_{z}^{z+h} \widehat{N} ̂(z') dz' \right) \mathrm{exp}⁡\left(\frac{h}{2}\widehat{D} \right)A(z,T),
\end

где экспоненциальный дисперсионный оператор легко переводится в спектральную область быстрым Фурье-преобразованием.
Принцип действия метода представлен на рисунке ниже.

Начальный импульс попадает в среду длиной , которая разбивается на участков с длиной . Расчет участка световода с длиной с известным импульсом на длине производится по следующему алгоритму:

  1. учитывается влияние дисперсии на половине шага в частотной области;
  2. вычисляется влияние нелинейности на полном шаге в середине шага;
  3. учитывается дисперсия на второй половине шага в частотной области.

ssfm_skhema2.png

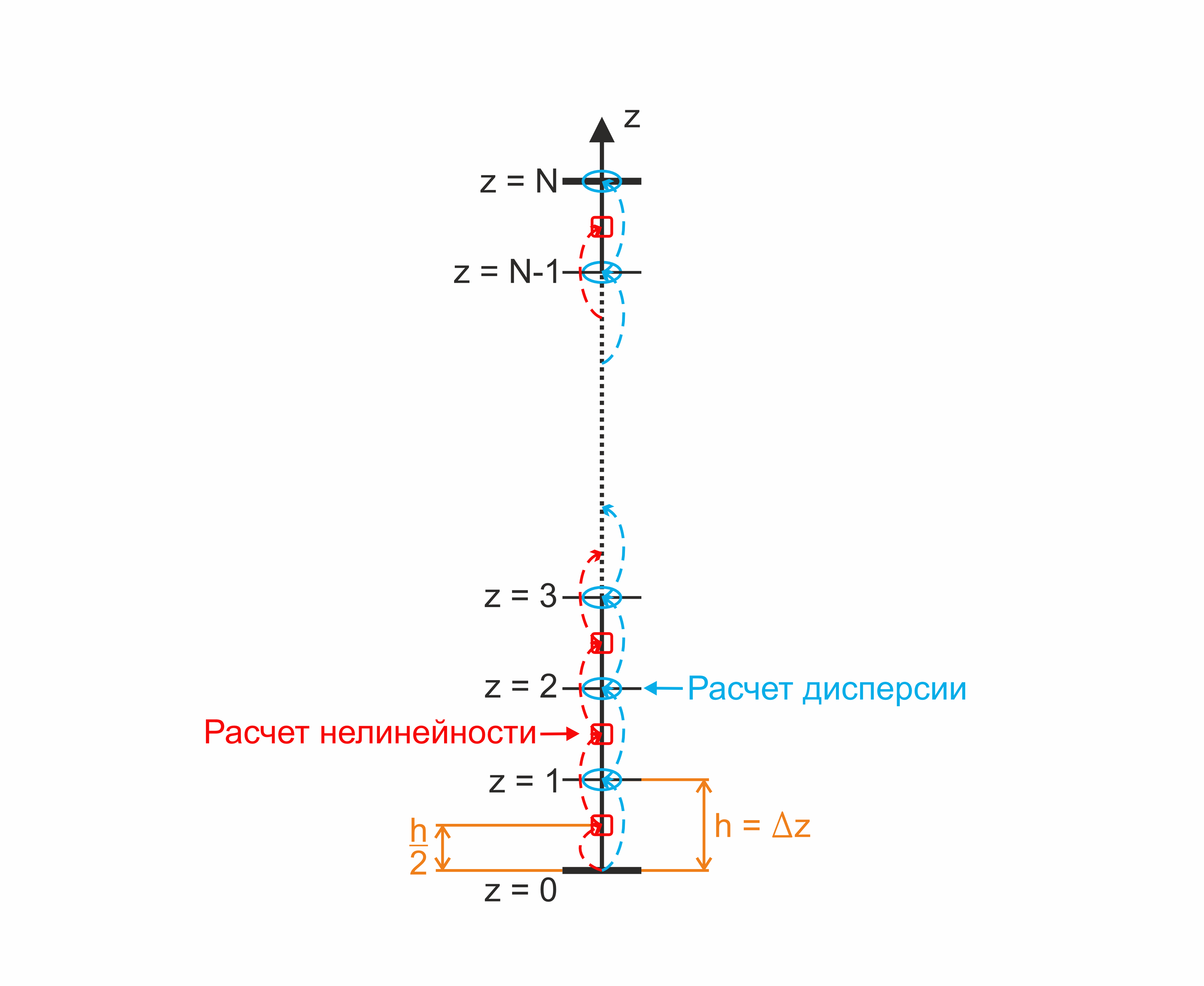
Поскольку операторы нелинейности и дисперсии некоммутативны, то решением будет только приближение, с полной погрешностью, определяемой квадратом шага [2].

Реализация фурье-метода расщепления по физическим факторам на языке Julia

Для реализации быстрого преобразования Фурье в Julia используется библиотека FFTW, для создания графиков — Plots.

In [ ]: 
using FFTW, Plots

Параметры волоконного световода

В качестве входных параметров для расчета зададим коэффициенты дисперсии и нелинейности кварцевого световода SMF-28. Параметры волоконного светода представлены для длины волны 1,55 мкм, применяемой для передачи сигналов в телекоммуникационных системах.

In [ ]: 
distance = 4  # Длина волокна, м
beta2 = -20e-3  # Коэффициент дисперсии групповых скоростей, пс^2/м
gamma = 2e-3; # Нелинейный параметр 1/Вт/м

Параметры расчетной сетки во временной и спектральных областях для численного расчета

Для проведения расчета необходимо создать параметры расчетной сетки во времени и частоте. Расчетная сетка во времени движется вместе с импульсом, где отрицательная половина отвечает за передний фронт импульса, а положительная - за задний. Сетка частот генерируется относительно центральной частоты излучения.

In [ ]: 
nt = 1024  # Количество точек FFT
Tmax = 16 # Размер временного окна, пс
step_num = 20000;  # Количество шагов расчета по z
step_saves = 100
deltaz = distance / step_num  # Шаг по z, м
dtau = (2 * Tmax) / nt  # Шаг по tau, пс

#--- Массивы для временной и частотной области
tau = (-nt/2:nt/2-1) * dtau;  # Временная сетка, пс
omega = (π / Tmax) * vcat(0:nt/2-1, -nt/2:-1);  # Частотная сетка, ТГц

Параметры импульса

Теперь мы можем сгенерировать начальный импульс. В качестве входного импульса зададим солитонный импульс, описываемый во временной области следующей формулой:
\begin{equation}
A(T) = \sqrt P sech(T/T_0),
\end{equation}
где - пиковая мощность импульса, Вт;
- время, пс;
- длительность импульса по уровню от максимальной интенсивности, пс.

In [ ]: 
#--- Профиль входного поля
Tfwhm = 0.5; # длительность импульса по уровню 1/2 от максимальной интенсивности, пс
T0 = Tfwhm./1.763; # полудлительность импульса по уровню 1/e от максимальной интенсивности, пс.
power = 1500 # Пиковая мощность импульса, Вт
uu = sqrt(power)*sech.(tau/T0);

Аллокация для хранения данных на каждом шаге и дисперсионный и нелинейный фазовые операторы

In [ ]: 
uu_evolution = zeros(nt, step_saves + 1)  # для хранения эволюции интенсивности во временной области
spectrum_evolution = zeros(nt, step_saves + 1)  # для хранения эволюции интенсивности в спектральной области

dispersion = exp.(0.5im * beta2 * omega.^2 * deltaz/2)  # Дисперсионный фазовый фактор
hhz = 1im * gamma * deltaz;  # Нелинейный фазовый фактор

Основной цикл расчета

In [ ]: 
# ********* [ Начало основного цикла] ***********
# Схема: 1/2N -> D -> 1/2N; первый полушаг нелинейный
temp = uu
uu_evolution[:, 1] = abs.(temp).^2
spectrum = fftshift(ifft(temp)) .* (nt * dtau) / sqrt(2*pi)
spectrum_evolution[:, 1] = abs.(spectrum).^2;

for k in 1:step_num
    # Выполняем шаг метода SSFM: дисперсионный, нелинейный, затем снова дисперсионный
    f_temp = ifft(temp) .* dispersion
    temp = fft(f_temp)
    temp = temp .* exp.(abs.(temp).^2 .* hhz)
    f_temp = ifft(temp) .* dispersion
    temp = fft(f_temp)
    if k % floor(step_num / step_saves) == 0
        # Сохраняем текущую интенсивность (abs(uu)^2) во временной области
        uu_evolution[:, Int(k / floor(step_num / step_saves)) + 1] = abs.(temp).^2
        # Рассчитываем спектр и сохраняем его для текущего шага
        spectrum = fftshift(ifft(temp)) .* (nt * dtau) / sqrt(2π)
        spectrum_evolution[:, Int(k / floor(step_num / step_saves)) + 1] = abs.(spectrum).^2
    end
end

Построение графиков

In [ ]: 
#---- Построение динамики во временной области
deltaz_saves = distance / step_saves
p1 = heatmap(tau, (1:step_saves) * deltaz_saves, uu_evolution', xlabel="Время, пс", ylabel="Длина волокна, м", title="Эволюция импульса во временной области", color=:inferno)

#---- Построение динамики в частотной области
p2 = heatmap(fftshift(omega) / (2 * π), (1:step_saves) * deltaz_saves, spectrum_evolution', xlabel="Частота, ТГц", ylabel="Длина волокна, м", title="Эволюция спектра в частотной области", color=:inferno)

#---- График импульса в начале и в конце во временной области
p3 = plot(tau, abs.(uu_evolution[:, 1]), label="Начало", linestyle=:dash, color=:blue, xlabel="Время, пс", ylabel="Интенсивность, Вт", title="Импульс во временной области")
plot!(p3, tau, abs.(uu_evolution[:, end]), label="Конец", linestyle=:solid, color=:red)

#---- График импульса в начале и в конце в частотной области
spectrum_start = spectrum_evolution[:, 1];
spectrum_end = spectrum_evolution[:, end];
p4 = plot(fftshift(omega) / (2 * π), abs.(spectrum_start).^2, label="Начало", linestyle=:dash, color=:blue, xlabel="Частота, ТГц", ylabel="Интенсивность, Вт/ТГц", title="Импульс в частотной области")
plot!(p4, fftshift(omega) / (2 * π), abs.(spectrum_end).^2, label="Конец", linestyle=:solid, color=:red);
In [ ]: 
plot(p1)
Out[0]:
In [ ]: 
plot(p2)
Out[0]:
In [ ]: 
plot(p3)
Out[0]:
In [ ]: 
plot(p4)
Out[0]:

Заключение

По полученным эволюциям импульса во временной и спектральной областях по длине распространения можно наблюдать действие двух явлений - фазовой самомодуляции (ФСМ) и дисперсии групповых скоростей (ДГС). ФСМ возникает вследствие зависимости константы распространения световода от интенсивности света, то есть нелинейным эффектом самовоздействия импульса. Ее проявление отражается в изменении формы спектра. ДГС влияет на длительность импульса во временной области.
Так как начальный импульс не имел чирпа, т.е. частотной модуляции, то в отсутствии ФСМ он уширялся бы, однако по эволюции импульса мы наблюдаем обратное. Этот эффект сжатия называется солитонным сжатием и проявляется на начальном этапе распространения в световоде, когда выполняется следующее соотношение (в нашем случае ). С помощью численной модели мы можем решить одну из возможных задач при построении волоконных лазерных систем - определить длину волокна, на котором импульс сжимается до минимальной длительности. В нашем случае она равна примерно 1,2 м, а длительность импульса составляет около 150 фс.

Таким образом, в данной проекте было предложено численное решение задачи по расчету динамики распространения ультракороткого импульса в волоконном световоде с у четом эффектов ФСМ и ДГС. Работа данной модели продемонстрирована на примере распространения солитонного импульса в световоде SMF-28. При надобности дисперсионный и нелинейный фазовые операторы могут быть дополнены другими членами, учитывающими поглощение, усиление, комбинационное рассеяние и т.д.

Список литературы

  1. Agrawal G.P. Nonlinear fiber optics // Nonlinear Fiber Optics. 2019.
  2. Beaud P. et al. Ultrashort pulse propagation, pulse breakup, and fundamental soliton formation in a single-mode optical fiber //IEEE journal of quantum electronics. – 1987. – Т. 23. – №. 11. – С. 1938-1946.
Группа видимости
ПубличноПросматривать контент могут все пользователи сообщества

Тип

Интерактивные скрипты

Краткое описание

Цель данного проекта состоит в решении задачи распространения ультракороткого импульса в кварцевом световоде SMF-28, широко использующемся в телекоммуникациях

Связанные материалы

Пусто

Теги

Категории

Расчеты в EngeeПрограммированиеJulia
Моделирование в Engee
Учебные дисциплиныНаучное направлениеФизика
МероприятияКонкурс работ Engee 2024

Языки

    Julia

Форматы

    ngscript

Уровень

    Средний

Статус

Опубликовано

Обновлено

Источник

Сообщество