Реконструкция сигнала в реальном времени с помощью ИИ
Реконструкция сигнала в режиме real-time
Существует широкий спектр задач, связанных с восстановлением измеренного сигнала, искажённого шумами, до его идеального состояния. Для этого чаще всего применяются рекуррентные нейронные сети, одномерные свёрточные сети и трансформеры.
Когда весь сигнал доступен заранее, можно использовать различные методы предобработки — фильтрацию, извлечение признаков и других статистик, которые затем подаются в нейросеть. Однако в ситуациях, когда данные поступают последовательно, в реальном времени, работать со всем сигналом целиком невозможно. Это усложняет применение свёрточных сетей, которые, как правило, требуют фиксированного сигнала, так как они работают с скользящими окнами.
В таких случаях можно использовать буфер фиксированной длины, который изначально заполнен нулями, а затем постепенно заполняется новыми значениями сигнала. Этот буфер выступает в роли скользящего окна: при поступлении нового элемента первое значение удаляется, остальные сдвигаются, и последнее место занимает новое измерение. Таким образом, свёрточная нейросеть получает доступ к локальному фрагменту сигнала, позволяя извлекать признаки даже в условиях поступающего потока данных.
Такой подход к использованию свёрточных сетей позволяет добиться приближенного к реальному времени режима работы. Однако у него есть один нюанс: первые N точек восстановленного сигнала (где N — длина буфера) могут быть искажены. Это связано с тем, что в начале буфер ещё не содержит достаточно информации — он заполнен нулями, и лишь по мере поступления новых значений начинает отражать реальные характеристики сигнала.
Подготовка к работе
Изначально импортируем все необходимые пакеты
include("$(@__DIR__)/packsges.jl")
using Pkg
Pkg.instantiate()
using Random, Plots, Interpolations, MAT, Statistics
using CUDA, cuDNN
using Flux
import Flux: Conv, Chain, relu, @functor
using ProgressMeter
using DataStructures
using Plots
using BSON
Генерация датасета
В данном примере используются синтетические данные, которые были получены с помощью функции generate_dataset. Эта функция генерирует заданное количество синтетических временных сигналов и сохраняет их в указанной папке
Каждый сигнал состоит из:
-
Гладкой траектории -
traj- полученной через интерполяцию случайных контрольных точек. -
Шумного сигнала -
traj_osc- к которому добавлена амплитудно- и частотно-модулированная синусоида.
Модуляция задаётся через случайно выбранную огибающую: затухающая, растущая или с импульсами.
function generate_dataset(N_samples, len_sample, outdir)
for i in 1:N_samples
try
t = 0:1:len_sample
ctrl_idx = 1:200:length(t)
ctrl_values = cumsum(randn(length(ctrl_idx))) .+ 25
traj = CubicSplineInterpolation(ctrl_idx, ctrl_values)(1:length(t))
pattern = rand([:decay, :grow, :bursts])
function envelope(pat, t)
if pat == :decay
return exp.(-t ./ 500)
elseif pat == :grow
return 1 .- exp.(-(maximum(t) .- t) ./ 500)
elseif pat == :bursts
s = zeros(length(t))
for (μ,s_,A) in [(200,80,0.5), (500,60,0.3), (800,70,0.4)]
s .+= A .* exp.(-0.5 .* ((t .- μ)./s_).^2)
end
return s ./ maximum(s)
else
return ones(length(t))
end
end
env_global = envelope(pattern, t)
amp_base = 0.8
env_slow = 0.3 .* sin.(2π*0.003 .* t)
amp_t = amp_base .* (1 .+ env_slow) .* env_global
freq_mean = 0.015
mod_slow = 0.2 .* sin.(2π*0.005 .* t)
inst_freq = freq_mean .* (1 .+ mod_slow) .* env_global
phase = cumsum(2π .* inst_freq)
oscill = amp_t .* sin.(phase)
traj_osc = traj .+ oscill
out_path = joinpath(outdir, "synthetic_traj_$(i).mat")
matwrite(out_path,
Dict("t" => Float32.(t),
"traj" => traj,
"traj_osc" => traj_osc))
catch
continue
end
end
end
outdir = joinpath(@__DIR__, "data");
mkpath(outdir)
N_samples = 2500
len_sample = 400
generate_dataset(N_samples, len_sample, outdir)
Каждый сгенерированные сигнал содержит 600 элементов. Поскольку идея - работа с буферами, нарежем сигнал на окна размером FRAME_LEN, соберем все данные в одну общую переменную и инициализируем загрузчики данных
FRAME_LEN = 16
batchsize = 64
initial_lr = 0.0003
file_list = filter(f -> endswith(f, ".mat"), readdir(outdir))
x_all = Vector{Vector{Float32}}()
y_all = Vector{Float32}()
for fname in file_list
data = matread(joinpath(outdir, fname))
Y = data["traj"]
f1 = data["traj_osc"]
for i in 1:(length(f1) - FRAME_LEN)
push!(x_all, f1[i : i + FRAME_LEN - 1])
push!(y_all, Y[i + FRAME_LEN - 1])
end
end
Визуализация наложения окон
random_fname = rand(file_list)
data = matread(joinpath(outdir, random_fname))
Y = data["traj"]
X = data["traj_osc"]
plot(Y, label="Эталонный сигнал")
plot!(X, label="Шумный сигнал")
x1, x2, x3 = x_all[1], x_all[2], x_all[3]
t1 = 1:FRAME_LEN
t2 = 2:(1+FRAME_LEN)
t3 = 3:(2+FRAME_LEN)
plot(t1, x1, label="x1", lw=4)
plot!(t2, x2, label="x2", lw=4)
plot!(t3, x3, label="x3", lw=4)
xlabel!("Время (отсчёты)")
ylabel!("Значение")
Окна с шагом в 1 - моделирование реального времени
Для формирования статистики окна вычисляются среднее и стандартное отклонение (СКО) по значениям внутри окна. В результате каждый сэмпл представляет собой трёхканальный тензор: первый канал — само окно сигнала, второй — вектор, заполненный средним значением, третий — вектор со СКО. Такой подход позволяет явно передать модели важные признаки, что облегчает обучение — ей не нужно извлекать их самостоятельно, так как они уже включены во входные данные.
@info "Всего примеров" length(x_all)
N = length(x_all)
X_tensor = zeros(Float32, 1, FRAME_LEN, N)
X_tensor = zeros(Float32, 3, FRAME_LEN, N)
Y_tensor = reshape(Float32.(y_all), 1, N) # (1, N)
for i in 1:N
x = Float32.(x_all[i])
μ = mean(x)
s = std(x)
X_tensor[1, :, i] .= x
X_tensor[2, :, i] .= μ
X_tensor[3, :, i] .= s
end
X_tensor = permutedims(X_tensor, (2, 1, 3))
idx = shuffle(1:N)
val_size = round(Int, 0.2N)
train_idx = idx[1:end-val_size]
val_idx = idx[end-val_size+1:end]
train_loader = Flux.DataLoader((X_tensor[:, :, train_idx], Y_tensor[:, train_idx]); batchsize=batchsize, shuffle=false)
val_loader = Flux.DataLoader((X_tensor[:, :, val_idx], Y_tensor[:, val_idx]); batchsize=batchsize, shuffle=false)
Модель ИНС
Код ниже реализует каузальную TCN-модель для шумоподавления.
Слой CausalConv1D — свёртка с каузальной паддингом, чтобы выход не зависел от будущих значений. Далее идёт ResBlock — два каузальных слоя с нелинейностями и возможным приведением размерностей.
Модель DenoiserTCN строится как цепочка таких блоков с нарастающими каналами и заканчивается сверточным слоем, сжимающим выход до одного канала.
struct CausalConv1D
conv::Conv
pad::Int
end
@functor CausalConv1D
function CausalConv1D(in_ch::Int, out_ch::Int, k::Int; dilation::Int=1)
pad = (k - 1) * dilation
CausalConv1D(Conv((k,), in_ch => out_ch;
pad=pad, dilation=dilation), pad)
end
(c::CausalConv1D)(x) = c.conv(x)[1:size(x,1), :, :]
struct ResBlock
conv1::CausalConv1D
conv2::CausalConv1D
rescale
end
@functor ResBlock
function ResBlock(in_ch::Int, out_ch::Int; k::Int=4, dilation::Int=1)
conv1 = CausalConv1D(in_ch, out_ch, k; dilation=dilation)
conv2 = CausalConv1D(out_ch, out_ch, k; dilation=dilation)
rescale = in_ch == out_ch ? x -> x : Conv((1,), in_ch => out_ch)
return ResBlock(conv1, conv2, rescale)
end
(m::ResBlock)(x) = relu.(m.conv2(relu.(m.conv1(x))) .+ m.rescale(x))
struct DenoiserTCN
net::Chain
end
@functor DenoiserTCN
function DenoiserTCN(hidden_sizes::Vector{Int}; k::Int=3)
dilations = [1, 2, 2, 2]
layers = Any[]
in_ch = 3
# in_ch = 1
for (hid, d) in zip(hidden_sizes, dilations)
push!(layers, ResBlock(in_ch, hid; k=k, dilation=d))
in_ch = hid
end
push!(layers, Conv((1,), in_ch => 1))
return DenoiserTCN(Chain(layers...))
end
(m::DenoiserTCN)(x) = m.net(x)[end, 1, :]
Подготовка к обучению
Инициализируем скорость обучения, оптимизатор, функцию потерь, а также переведем нашу модель на тот девайс, который доступен в Engee
device = CUDA.functional() ? gpu : cpu;
model = DenoiserTCN([512, 512, 512, 512]);
model = device(model);
opt = Flux.Adam(initial_lr, (0.9, 0.99));
lossFunction(x, y) = Flux.Losses.huber_loss(x, y);
Определим функцию, которая выполняет тренировку на одной эпохе
function train!(
model, train_loader, opt, loss_fn,
device, epoch::Int, num_epochs::Int
)
running_loss = 0.0
n_batches = 0
total_batches = length(train_loader)
step = ceil(Int, total_batches * 0.2)
for (i, data) in enumerate(train_loader)
if i % step == 0
pct = round(i/total_batches*100)
println("Epoch $epoch/$num_epochs — batch $i/$total_batches ($pct %)")
end
x, y = data |> device
loss_val, gs = Flux.withgradient(Flux.params(model)) do
ŷ = model(x)
lossFunction(ŷ, dropdims(y, dims=1))
end
Flux.update!(opt, Flux.params(model), gs)
running_loss += Float64(loss_val)
n_batches += 1
end
train_loss = running_loss / max(n_batches, 1)
return opt, train_loss
end;
Обучение модели
no_improve_epochs = 0
best_model = nothing
train_losses = [];
valid_losses = [];
best_val_loss = Inf;
num_epochs = 50
for epoch in 1:num_epochs
println("-"^50 * "\n")
println("EPOCH $(epoch):")
opt, train_loss = train!(
model, train_loader, opt,
lossFunction, device, epoch, num_epochs
)
println("Epoch $epoch/$num_epochs | train $(round(train_loss, digits=4))")
push!(train_losses, train_loss)
end
Сохраним обученную модель в указанную директорию
@info "Saving best model"
outdirsave = joinpath(@__DIR__, "models");
best_path = joinpath(outdirsave,"model2final.bson")
model = cpu(model)
@BSON.save best_path model
Тестирование модели
Сгенерируем для теста новые сигналы, которых не видела модель
outdir = joinpath(@__DIR__, "data_test");
mkpath(outdir)
N_samples = 10
len_sample = 400
generate_dataset(N_samples, len_sample, outdir)
Выберем из папки случайный сигнал, на котором проведем тесты
outdirsave = joinpath(@__DIR__, "models");
best_path = joinpath(outdirsave,"model2final.bson")
@BSON.load best_path model
outdirtest = joinpath(@__DIR__, "data_test");
file_list = readdir(outdirtest)
random_fname = rand(file_list)
data = matread(joinpath(outdirtest, random_fname))
Y = data["traj"]
f1 = data["traj_osc"]
clean, noisy = Y, f1
frame_len = 16
buf = CircularBuffer{Float32}(frame_len)
fill!(buf, 0f0);
preds = [];
modelTest = gpu(model);
Ну и выполним инференс модели, результаты отобразим на графике ниже
for s in noisy
push!(buf, s)
x = collect(buf)
μ, s = mean(x), std(x)
mean_vec = fill(μ, frame_len)
std_vec = fill(s, frame_len)
x_input = reshape(vcat(x, mean_vec, std_vec), (frame_len, 3, 1))
x_input = gpu(x_input)
pred = modelTest(x_input)
push!(preds, pred)
end
preds = vec(cpu(preds))
rec = Float32[x[1] for x in preds];
Для визуализации того, как работает модель в реальном времени, создадим GIF, которая показывает точку (красным цветом), которую на каждом шаге наполнения буфера предсказывает модель
x_preds = (frame_len-1):(frame_len-1+length(preds)-1)
preds_ = [i[1] for i in preds]
all_vals = reduce(vcat, (clean, noisy, preds_))
ymin, ymax = extrema(all_vals)
default(size = (1000, 400))
anim = @animate for k in 1:length(preds)
i = k + frame_len - 1
p = plot(x_preds, noisy; label="noisy", alpha=0.4)
plot!(p, x_preds, clean; label="clean", lw=1)
plot!(p, x_preds[frame_len: end], preds_[frame_len: end]; label="preds", alpha=0.4)
vspan!(p, i-frame_len+1, i; color=:gray, opacity=0.15, label="")
if k > frame_len
scatter!(p, [i], [preds_[k]]; color=:red, ms=4, label="")
end
title!(p, "Real-time inference demo")
end every 1
gif(anim, "realtime_inference_demo.gif", fps=10)
println("GIF saved to realtime_inference_demo.gif")
Посмотри на GIF
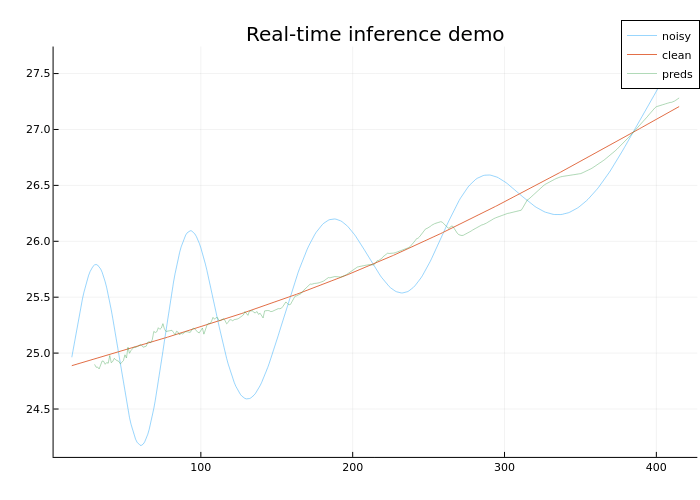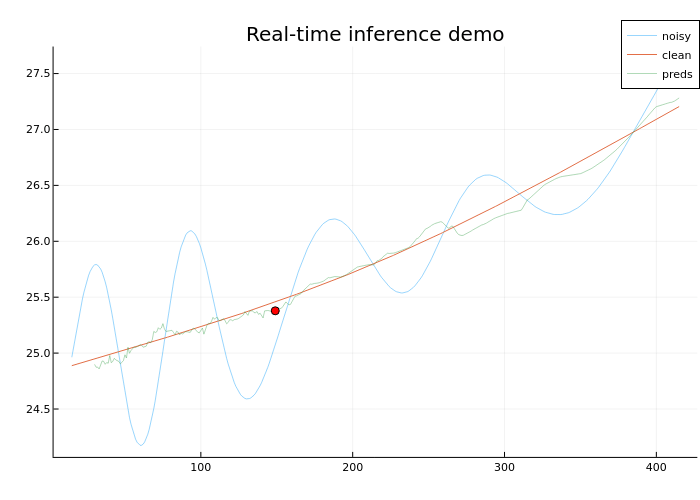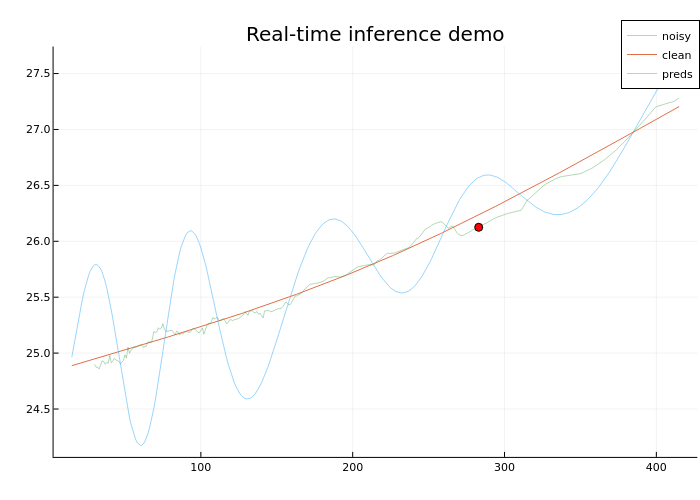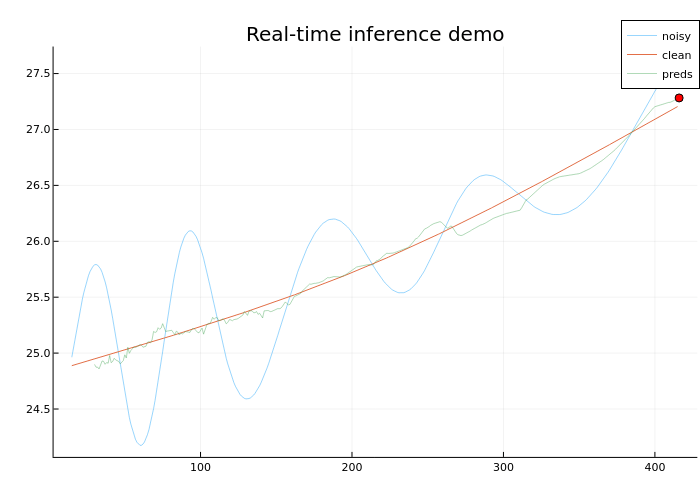
Результаты работы модель можно улучшить, важно подобрать правильную архитектуру, гиперпараметры, а также можно выполнить предобработку данных перед обучением модели, чтобы зашумленный сигнал имел более высокую корреляцию с эталонным сигналом
Выводы
В данной работе было разобрано, как с помощью казуальных сверток, которые не заглядывают в будущее сигнала, а работают только с накопившимся буфером, можно сделать восстановления сигнала из зашумленного