Решение экономических оптимизационных задач в Julia Engee
Решение оптимизационных задач в экосистеме Julia Engee
В данной работе на примерах решения оптимизационных задач в основном в области экономики показаны соответствующие возможности экосистемы Julia . Содержательные постановки задач взяты из книги И.Ф.Цисарь,В.Г.Нейман "Компьютерное моделирование экономики",а также из работ автора и некоторых других источников.
Задача 1 : Найти min функции Розенброка
Здесь необходимо найти :
Это хорошо известная задача для тестирования различных алгоритмов нелинейной оптимизации. Ниже представлены скрипты, демонстрирующие возможности некоторых алгоритмов нелинейной локальной и глобальной оптимизации, которые доступны в Julia
using JuMP, Ipopt
model = Model(Ipopt.Optimizer)
set_silent(model)
@variable(model, x, start=0.3)
@variable(model, y, start=0.4)
@NLobjective(model, Min,(1-x)^2 + 100 * (y-x^2)^2)
@constraint(model, x + y == 2.0)
@NLconstraint(model, x*y == 1.0)
JuMP.optimize!(model)
@show JuMP.termination_status(model)
@show JuMP.primal_status(model)
@show JuMP.objective_value(model)
@show JuMP.value(x)
@show JuMP.value(y)
x1 =collect(range(-5,5,100));
y1 =collect(range(-5,5,100));
f(x1,y1)= ((1-x1)^2) + (100*(y1-x1^2)^2)
X=[JuMP.value(x)]
Y=[JuMP.value(y)]
Xopt=round(X[1];digits = 1)
Yopt=round(Y[1];digits = 1)
Xopt=string(Xopt)
Yopt=string(Yopt)
fopt="[xopt,yopt]="*"["*Xopt*Yopt*"]";
#ГРАФИК РЕШЕНИЯ
using Plots,PlotThemes
plotly()
theme(:dao)
surface(x1, y1,f, linewidth=3,legend=:topleft, wsize=(600, 450))
scatter!(X,Y,[(1-X[1])^2 + 100 * (Y[1]-X[1]^2)^2], label=fopt, mc=:red, ms=4, ma=0.8)
title!("Функция Розенброка F")
using JuMP, NLopt
model = Model(NLopt.Optimizer)
set_attribute(model, "algorithm", :LN_COBYLA)
set_attribute(model, "xtol_rel", 1e-4)
set_attribute(model, "constrtol_abs", 1e-8)
@variable(model, x[1:2])
set_start_value.(x,[0.0,0.0])
@NLobjective(model, Min, (1-x[1])^2 + 100 * (x[2]-x[1]^2)^2)
@NLconstraint(model, x[1] + x[2] == 2.0)
@NLconstraint(model, x[1]*x[2] == 1.0)
JuMP.optimize!(model)
min_f, min_x, ret = objective_value(model), value.(x), raw_status(model)
println(
"""
objective value : $min_f
solution : $min_x
solution status : $ret
"""
)
using NLopt
function rosenbrock(x::Vector,grad::Vector)
return (1.0 - x[1])^2 + 100.0*(x[2]-x[1]^2)^2
end
#p = [1.0, 100.0]
x0=[0.1, 0.03]
function ogrf1(x::Vector,grad::Vector,a)
return x[1] + x[2]-a
end
function ogrf2(x::Vector,grad::Vector,b)
return x[1]*x[2]-b
end
opt = NLopt.Opt(:GN_ISRES, 2) #GN_ISRES LN_COBYLA
NLopt.lower_bounds!(opt, [-1.0, -1.0])
NLopt.upper_bounds!(opt, [1.0, 1.0])
NLopt.xtol_rel!(opt, 1e-4)
NLopt.min_objective!(opt, rosenbrock)
NLopt.inequality_constraint!(opt,(x,g) -> ogrf1(x,g,2), 1e-8)
NLopt.inequality_constraint!(opt, (x,g) -> ogrf2(x,g,1), 1e-8)
min_f, min_x, ret = NLopt.optimize(opt, x0)
num_evals = NLopt.numevals(opt)
println(
"""
objective value : $min_f
solution : $min_x
solution status : $ret
# function evaluation : $num_evals
"""
)
Рассмотрим более интересную функцию, у которой имеется несколько минимумов. Ниже представлен скрипт где для поиска min используется алгоритм LN_COBYLA локальной оптимизации из библиотеки NLopt. На графике мы хорошо видит, что этот алгоритм нашел точку локального min.
using NLopt
function glabf(x::Vector,grad::Vector)
return 3 * exp(-(3x[1]^2 + x[2]^2)/5) * (sin(x[1]+2x[2]))
end
x0=[0.43, 0.58]
opt = NLopt.Opt(:LN_COBYLA, 2) #GN_ISRES LN_COBYLA
NLopt.lower_bounds!(opt, [ -0.8*π, -0.8*π])
NLopt.upper_bounds!(opt, [ 0.8*π, 0.8*π])
NLopt.xtol_rel!(opt, 1e-4)
NLopt.min_objective!(opt, glabf)
min_f, min_x, ret = NLopt.optimize(opt, x0)
num_evals = NLopt.numevals(opt)
println(
"""
objective value : $min_f
solution : $min_x
solution status : $ret
# function evaluation : $num_evals
"""
)
#локальныйный минимум график
#начальная точка
x0=[0.43, 0.58]
X0=[x0[1]]
Y0=[x0[2]]
z0=3 * exp(-(3x0[1]^2 + x0[2]^2)/5) * (sin(x0[1]+2x0[2]))
Z0=[z0]
# точка локального минимума
x1=[min_x[1]]
y1=[min_x[2]]
z=[min_f]
using Plots; plotly()
theme(:dao)
x = y = collect(range(-0.8*π, 0.8*π; length = 100))
fn(x, y) = 3 * exp(-(3x^2 + y^2)/5) * (sin(x+2y))
surface(x, y, fn, c=:viridis,fillalpha = 0.95,legend=:topleft,wsize=(750, 450), extra_kwargs=Dict(:subplot=>Dict("3d_colorbar_axis" => [0.9, 0.05, 0.05, 0.9])))
scatter!(x1, y1, z,label="Локальный min", mc=:red, ms=4, ma=0.8)
scatter!(X0, Y0, Z0,label="Начальная точка", mc=:blue, ms=4, ma=0.8)
title!(" Пример локального min функции со сложной топологией")
Выберем ту же начальную точку, но используем алгоритм глобальной оптимизации GN_ISRES из библиотеки NLopt. Этот алгоритм обеспечил нам нахождение глобального min, это хорошо видно на графике. Рассмотрим еще один алгоритм глобальной оптимизации SAMIN()(имитация отжига с ограничениями коробка) из библиотеки Optim. Алгоритм не сошелся хотя финишные значения близки к глобальному min. Для настройки этого алгоритма нужно задавать большое количество специфических параметров,а это неудобно и в последствии в работе алгоритмы из этой библиотеки не используются.
using NLopt
function glabf(x::Vector,grad::Vector)
return 3 * exp(-(3x[1]^2 + x[2]^2)/5) * (sin(x[1]+2x[2]))
end
x0=[0.43, 0.58]
opt = NLopt.Opt(:GN_ISRES, 2) #GN_ISRES LN_COBYLA
NLopt.lower_bounds!(opt, [ -0.8*π, -0.8*π])
NLopt.upper_bounds!(opt, [ 0.8*π, 0.8*π])
NLopt.xtol_rel!(opt, 1e-4)
NLopt.min_objective!(opt, glabf)
min_f, min_x, ret = NLopt.optimize(opt, x0)
num_evals = NLopt.numevals(opt)
println(
"""
objective value : $min_f
solution : $min_x
solution status : $ret
# function evaluation : $num_evals
"""
)
#глобальный минимум график
#начальная точка
X0=[x0[1]]
Y0=[x0[2]]
z0=3 * exp(-(3x0[1]^2 + x0[2]^2)/5) * (sin(x0[1]+2x0[2]))
Z0=[z0]
#точка глобального минимума
x1=[min_x[1]]
y1=[min_x[2]]
z=[min_f]
using Plots; plotly()
theme(:dao)
x = y = collect(range(-0.8*π, 0.8*π; length = 100))
fn(x, y) = 3 * exp(-(3x^2 + y^2)/5) * (sin(x+2y))
surface(x, y, fn, c=:viridis,fillalpha = 0.95,legend=:topleft,wsize=(750, 450), extra_kwargs=Dict(:subplot=>Dict("3d_colorbar_axis" => [0.9, 0.05, 0.05, 0.9])))
scatter!(x1, y1, z,label="глобальный min", mc=:red, ms=4, ma=0.8)
scatter!(X0, Y0, Z0,label="Начальная точка", mc=:blue, ms=4, ma=0.8)
title!(" Пример глобального min функции со сложной топологией")
#Глобальный оптимизатор
#Optim.SAMIN(): Имитация отжига с ограничениями коробка
using Optim
f(x) = 3 * exp(-(3x[1]^2 + x[2]^2)/5) * (sin(x[1]+2x[2]))
function main()
x0 = [0.43, 0.58]
obj = x -> f(x)
lb = [ -0.8*π, -0.8*π]
ub = [0.8*π,0.8*π]
prob = Optim.optimize(obj, lb, ub, x0, SAMIN(nt=5,ns=4,rt=0.8,neps=4),
Optim.Options(x_tol = 1e-6,f_tol = 1e-6,iterations=10000,store_trace = true,
show_trace=false,extended_trace=false,show_every=1))
end
main()
Задача 2:
Из листа бумаги заданного размера (a – ширина листа, b –длина листа) необходимо изготовить коробочку (без крышки) в форме правильного прямоугольного параллелепипеда максимального объема.
Построение математической модели
Для построения модели для заданной задачи графически изобразим процесс изготовления коробки из листа бумаги шириной a и высотой b.
Представим это в виде рисунка 1. Как видно из рисунка 1, при фиксированных ширине и высоте листа единственным параметром от которого зависит объем создаваемой коробки будет величина её высоты x. Схема раскроя листа, проводит нас к следующей оптимизационной задаче:
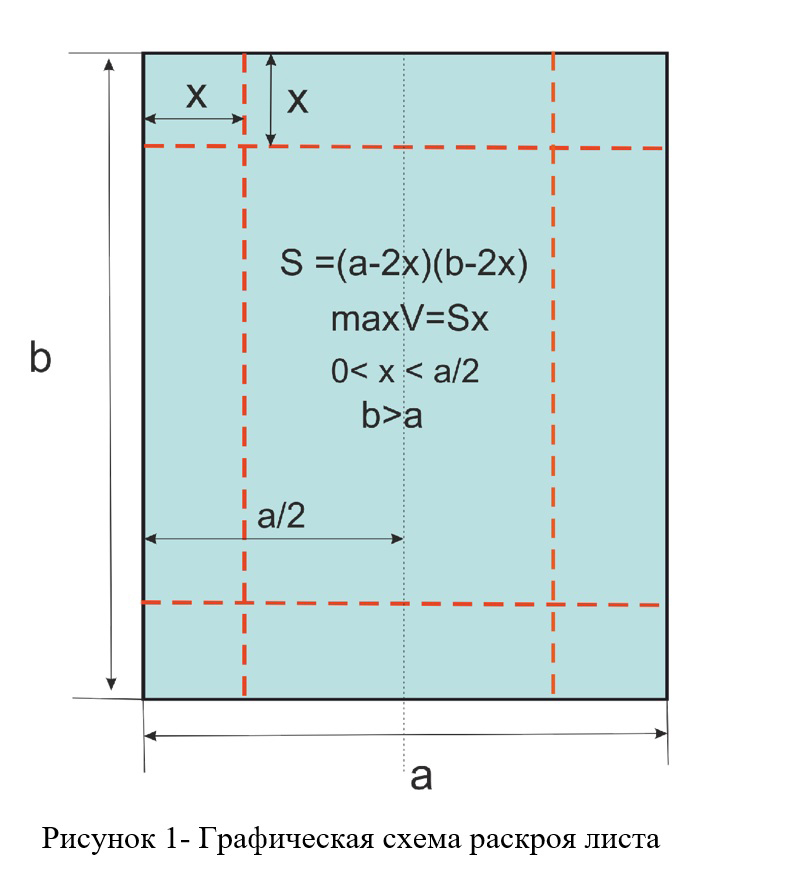
Ниже приведен скрипт Julia, который решает эту оптимизационную задачу с помощью пакетов JuMP и Ipopt, для вводимых в режиме диалога значений и .
#максимальный объем коробки из листа a X b
using JuMP, Ipopt
n1 = 50
n2 = 50
xmax = zeros(n1, n2)
Vmax = zeros(n1, n2)
print("Введите ширину листа:1,2,3,4,5,6,7,...,$n1 \n")
num1 = readline()
a = tryparse(Int64, num1);
println("Ширина = ", a)
print("Введите высоту листа:1,2,3,4,5,6,7,...,$n2 \n")
num2 = readline()
b = tryparse(Int64, num2);
println("Высота = ", b);
if a <= b
model = Model(Ipopt.Optimizer)
set_silent(model)
@variable(model, x, start = 0.01)
@NLobjective(model, Max, 4x^3 - 2b * x^2 - 2*a * x^2 + a * b * x)
@constraint(model, x <= a/2)
JuMP.optimize!(model)
Vmax[a,b] = JuMP.objective_value(model)
xmax[a,b] = JuMP.value(x)
else
println("a > b")
xmax[a,b] = 0.0
Vmax[a,b] = 0.0
end
println("xmax=", xmax[a,b])
println("Vmax=", Vmax[a,b])
Задача 3 Определения оптимального портфеля ценных бумаг.
ПОСТАНОВКА И РЕШЕНИЕ ЗАДАЧИ ОПРЕДЕЛЕНИЯ ОПТИМАЛЬНОГО ПОРТФЕЛЯ АКТИВОВ В ВАРИАНТЕ КАННЕМАНА-ТВЕРСКИ
Перечень входных параметров
alfa = 0.90 – коэффициент избегания риска на положительной части целевой функции;
beta = 0.88 – коэффициент избегания риска на отрицательной части целевой функции;
lambda = 1.25 – коэффициент избегания потерь;
=0.99∈(rср_min,rср_max) - граница доходности портфеля, выше, которой мы считаем, что получаем прибыль
Перечень переменных:
- доля каждой -ой акции в портфеле (=92);
Целевая функция и ограничения:
где - число периодов времени (в нашем случае =290); – функция полезности в момент времени .
-число акций в портфеле (в нашем случае =92), – потенциальное число акций, которые могут быть включены в портфель и матрица доходности = транспонированной Data_set2.xlsx
Задача решается при следующих ограничениях:
Для решения задачи были разработаны несколько простых скриптов julia.
#РАСЧЕТ ИСХОДНЫХ ДАННЫХ ДЛЯ ЗАДАЧИ ПОРТФЕЛЬ ЦЕННЫХ БУМАГ
import XLSX
using DataFrames
using Statistics
global T = 290
global K = 92
global r = zeros(K)
global x = zeros(K)
global Sr = zeros(K)
#ввод МАТРИЦЫ ДОХОДНОСТИ АКЦИЙ
DOH2_AK = XLSX.readxlsx("/user/Optimum/Data_set2.xlsx")
DOH2_AK = DOH2_AK["dan01"]
RR = DOH2_AK[2:T+1, 2:K+1]
R = Float64.(RR)
Rv = R
R = R'
#РАСЧЕТ ОЖИДАЕМЫХ ДОХОДНОСТЕЙ
for i in 1:K
r[i] = mean(R[i, 1:end])
end
#ОПРЕДЕЛЕНИЕ МИН И МАХ ДОХОДНОСТЕЙ
rcp_min = minimum(r)
rcp_max = maximum(r)
r_min = minimum(R)
r_max = maximum(R)
#РАСЧЕТ КОВАРИЦИОННОЙ МАТРИЦЫ ДОХОДНОСТЕЙ
V = cov(Rv);
println("Исходные данные сформированы")
Приведенный выше скрипт предназначен для расчета следующих величин:
-
вектора столбца ожидаемых доходностей и ;
-
минимального и максимального значения доходности ;
-
ковариационной матрицы .
#ЦЕЛЕВАЯ ФУНКЦИЯ
function yu(x)
#задание параметров
alfa = 0.90
beta = 0.88
lambda = 1.25
r0 = 0.99
Dat = R
u = zeros(T)
uu = zeros(T)
#формирование функции полезности
for i in 1:T
for j in 1:K
u[i] = u[i] + Dat[j, i] * x[j]
end
end
for i in 1:T
if (u[i] - r0) >= 0
uu[i] = (u[i] - r0)^alfa
else
uu[i] = -lambda * (r0 - u[i])^beta
end
end
s = 0
for j in 1:T
s = s + uu[j]
end
yu = s / T
end
#ОГРАНИЧЕНИЯ
function x_ogr1(x::Vector)
sum(x) - 1 < 0.05
end
function x_ogr2(x::Vector)
r_ogr = 1.0001
S = 0.0
for i in 1:K
Sr[i] = 0.0
for j in 1:T
Sr[i] = Sr[i] + R[i, j]
end
Sr[i] = (Sr[i] / T) * x[i]
S = Sr[i] + S
end
S - r_ogr >= -0.00004
end
println("Целевая функция и ограничичения заданы")
Данный скрипт задает целевую функцию и ограничения
#ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОГО ПОРТФЕЛЯ МЕТОДОМ МОНТЕ КАРЛО
using Distributions
using BenchmarkTools
N = 10000
Yopt = 0.0
for l in 1:N
dist = Distributions.Uniform(-2.0,1.5)
x = Distributions.rand(dist, K)
global nl=l
for j in 1:K
if x[j] < 0.0
x[j] = 0.0
end
end
Sx = 0.0
for i in 1:K
if x[i] > 0.0
Sx = x[i] + Sx
end
end
for i in 1:K
if x[i] > 0.0
x[i] = x[i] / Sx
end
end
if x_ogr1(x) == true
if x_ogr2(x) == true
if yu(x) > Yopt
Yopt = yu(x)
println("Итерация № $nl , Yopt= $Yopt")
end
end
end
end
println("nl=$nl")
@show x_ogr1(x)
@show x_ogr2(x)
@show Yopt;
# печать решения
for j in 1:K
println(x[j])
end
Данный скрипт реализует поиск решения методом Монте Карло
#ГРАФИК РЕШЕНИЯ
using Plots, PlotThemes
plotly()
theme(:ggplot2)
Time=2.5
Time = round(Time; digits=3)
X = 1:K
Y = x[1:K]*100
Yopt = round(Yopt; digits=5)
function bar1()
data = bar(X, Y, label="%")
plot(data, wsize=(950, 500))
ylabel!("Процет акций в портфеле")
xlabel!("Номер акции")
title!("Портфель ЦБ, Yopt=$Yopt, K=$K, N=$nl , Ntime ≈ $Time мин.")
end
bar1()
Скрипт, представленный выше, строит график полученного решения. При числе ценных бумаг в портфеле K=92, мы получили это решение, задав число реализаций и время приблизительно 2.5 мин.То есть, использование метода Монте Карло для решения задачи оптимизации портфеля ЦБ относительно трудозатратно и качество получаемого решения очень сильно зависит от значений , , закона распределения и его параметров, обеспечивающих генерацию варианта решения на каждой реалиализации алгоритма.
Попробуем решить задачу поиска оптимального портфеля ЦБ при K=10 методами Монте Карло и используя алгоритмы GN_ISRES LN_COBYLA из библиотеки NLopt
#РАСЧЕТ ИСХОДНЫХ ДАННЫХ ДЛЯ ЗАДАЧИ ПОРТФЕЛЬ ЦЕННЫХ БУМАГ
import XLSX
using DataFrames
using Statistics
global T = 290
global K = 10
global r = zeros(K)
global x = zeros(K)
global Sr = zeros(K)
#ввод МАТРИЦЫ ДОХОДНОСТИ АКЦИЙ
DOH2_AK = XLSX.readxlsx("/user/Optimum/Data_set2.xlsx")
DOH2_AK = DOH2_AK["dan01"]
RR = DOH2_AK[2:T+1, 2:K+1]
R = Float64.(RR)
Rv = R
R = R'
#РАСЧЕТ ОЖИДАЕМЫХ ДОХОДНОСТЕЙ
for i in 1:K
r[i] = mean(R[i, 1:end])
end
#ОПРЕДЕЛЕНИЕ МИН И МАХ ДОХОДНОСТЕЙ
rcp_min = minimum(r)
rcp_max = maximum(r)
r_min = minimum(R)
r_max = maximum(R)
#РАСЧЕТ КОВАРИЦИОННОЙ МАТРИЦЫ ДОХОДНОСТЕЙ
V = cov(Rv);#РАСЧЕТ ИСХОДНЫХ ДАННЫХ ДЛЯ ЗАДАЧИ ПОРТФЕЛЬ ЦЕННЫХ БУМАГ
import XLSX
using DataFrames
using Statistics
global T = 290
global K = 10
global r = zeros(K)
global x = zeros(K)
global Sr = zeros(K)
#ввод МАТРИЦЫ ДОХОДНОСТИ АКЦИЙ
DOH2_AK = XLSX.readxlsx("Data_set2.xlsx")
DOH2_AK = DOH2_AK["dan01"]
RR = DOH2_AK[2:T+1, 2:K+1]
R = Float64.(RR)
Rv = R
R = R'
#РАСЧЕТ ОЖИДАЕМЫХ ДОХОДНОСТЕЙ
for i in 1:K
r[i] = mean(R[i, 1:end])
end
#ОПРЕДЕЛЕНИЕ МИН И МАХ ДОХОДНОСТЕЙ
rcp_min = minimum(r)
rcp_max = maximum(r)
r_min = minimum(R)
r_max = maximum(R)
#РАСЧЕТ КОВАРИЦИОННОЙ МАТРИЦЫ ДОХОДНОСТЕЙ
V = cov(Rv);
println("Исходные данные сформированы")
#ЦЕЛЕВАЯ ФУНКЦИЯ И ОГРАНИЧЕНИЯ ДЛЯ АЛГОРИТМА МОНТЕ-КАРЛО
function yu(x)
#задание параметров
alfa = 0.90
beta = 0.88
lambda = 1.25
r0 = 0.99
Dat = R
u = zeros(T)
uu = zeros(T)
#формирование функции полезности
for i in 1:T
for j in 1:K
u[i] = u[i] + Dat[j, i] * x[j]
end
end
for i in 1:T
if (u[i] - r0) >= 0
uu[i] = (u[i] - r0)^alfa
else
uu[i] = -lambda * (r0 - u[i])^beta
end
end
s = 0
for j in 1:T
s = s + uu[j]
end
yu = s / T
end
#ОГРАНИЧЕНИЯ
function x_ogr1(x::Vector)
sum(x) - 1 < 0.05
end
function x_ogr2(x::Vector)
r_ogr = 1.0001
S = 0.0
for i in 1:K
Sr[i] = 0.0
for j in 1:T
Sr[i] = Sr[i] + R[i, j]
end
Sr[i] = (Sr[i] / T) * x[i]
S = Sr[i] + S
end
S - r_ogr >= -0.00004
end
println("Целевая функция и ограничичения заданы для МК")
#ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОГО ПОРТФЕЛЯ МЕТОДОМ МОНТЕ КАРЛО
using Distributions
using BenchmarkTools
N = 100000
Yopt = 0.0
#Random.seed!(456)
for l in 1:N
#dist = Distributions.Normal(0.5, 2.0)
dist = Distributions.Uniform(-2.0,1.5)
x = Distributions.rand(dist, K)
global nl=l
for j in 1:K
if x[j] < 0.0
x[j] = 0.0
end
end
Sx = 0.0
for i in 1:K
if x[i] > 0.0
Sx = x[i] + Sx
end
end
for i in 1:K
if x[i] > 0.0
x[i] = x[i] / Sx
end
end
if x_ogr1(x) == true
if x_ogr2(x) == true
if yu(x) > Yopt
Yopt = yu(x)
println("Итрация № $nl , Yopt= $Yopt")
end
end
end
end
println("nl=$nl")
@show x_ogr1(x)
@show x_ogr2(x)
@show Yopt;
#ГРАФИК РЕШЕНИЯ
using Plots, PlotThemes
plotly()
theme(:ggplot2)
Time=2.0
Time = round(Time; digits=1)
X = 1:K
Y = x[1:K]*100
Yopt = round(Yopt; digits=5)
function bar1()
data = bar(X, Y, label="%")
plot(data, wsize=(850, 400))
ylabel!("Процет акций в портфеле")
xlabel!("Номер акции")
title!("xopt (алгоритм Монте Карло),Yopt=$Yopt, K=$K, N=$nl, Ntime≈$Time мин.")
end
bar1()
using NLopt
using Distributions
function yu(x::Vector,grad::Vector)
#задание параметров
alfa = 0.90
beta = 0.88
lambda = 1.25
r0 = 0.99
Dat = R
u = zeros(T)
uu = zeros(T)
#формирование функции полезности
for i in 1:T
for j in 1:K
u[i] = u[i] + Dat[j, i] * x[j]
end
end
for i in 1:T
if (u[i] - r0) >= 0
uu[i] = (u[i] - r0)^alfa
else
uu[i] = -lambda * (r0 - u[i])^beta
end
end
s = 0
for j in 1:T
s = s + uu[j]
end
return -(s / T)
end
#ОГРАНИЧЕНИЯ
function ogrf1(x::Vector,grad::Vector,a)
return sum(x)- a
end
function ogrf2(x::Vector,grad::Vector,b)
#r_ogr = 1.0001
S = 0.0
for i in 1:K
Sr[i] = 0.0
for j in 1:T
Sr[i] = Sr[i] + R[i, j]
end
Sr[i] = (Sr[i] / T) * x[i]
S = Sr[i] + S
end
return -S+b
end
#dist = Distributions.Uniform(0.0,1.0)
#x0 = Distributions.rand(dist, K)
x0=zeros(K)
lb = [0.0, 0.0,0.0, 0.0, 0.0, 0.0, 0.0,0.0, 0.0, 0.0]
ub = [1.0, 1.0, 1.0,1.0, 1.0, 1.0, 1.0, 1.0,1.0, 1.0]
opt = NLopt.Opt(:LN_COBYLA, K) #GN_ISRES LN_COBYLA
NLopt.lower_bounds!(opt,lb)
NLopt.upper_bounds!(opt,ub)
NLopt.xtol_rel!(opt, 1e-4)
NLopt.min_objective!(opt, yu)
NLopt.inequality_constraint!(opt,(x,g) -> ogrf1(x,g,1.0), 1e-6)
NLopt.inequality_constraint!(opt, (x,g) -> ogrf2(x,g,1.003), 1e-6)
min_f, min_x, ret = NLopt.optimize(opt, x0)
num_evals = NLopt.numevals(opt)
println(
"""
objective value : $min_f
solution : $min_x
solution status : $ret
# function evaluation : $num_evals
"""
)
@show round(ogrf1(min_x,[],1.0); digits=4)
@show round(ogrf2(min_x,[],1.001); digits=3)
@show round(sum(min_x);digits=4);
#ГРАФИК РЕШЕНИЯ LN_COBYLA
using Plots, PlotThemes
plotly()
theme(:ggplot2)
X = 1:K
Y = min_x[1:K]*100
@show Yopt = -round(min_f; digits=4)
function bar1()
data = bar(X, Y, label="%")
plot(data, wsize=(950, 500))
ylabel!("Процет акций в портфеле")
xlabel!("Номер акции")
title!("xopt (алгоритм LN_COBYLA),Yopt=$Yopt, K=$K, Ntime≈ 2 с.")
end
bar1()
using NLopt
using Distributions
function yu(x::Vector,grad::Vector)
#задание параметров
alfa = 0.90
beta = 0.88
lambda = 1.25
r0 = 0.99
Dat = R
u = zeros(T)
uu = zeros(T)
#формирование функции полезности
for i in 1:T
for j in 1:K
u[i] = u[i] + Dat[j, i] * x[j]
end
end
for i in 1:T
if (u[i] - r0) >= 0
uu[i] = (u[i] - r0)^alfa
else
uu[i] = -lambda * (r0 - u[i])^beta
end
end
s = 0
for j in 1:T
s = s + uu[j]
end
return -(s / T)
end
#ОГРАНИЧЕНИЯ
function ogrf1(x::Vector,grad::Vector,a)
return sum(x)- a
end
function ogrf2(x::Vector,grad::Vector,b)
#r_ogr = 1.0001
S = 0.0
for i in 1:K
Sr[i] = 0.0
for j in 1:T
Sr[i] = Sr[i] + R[i, j]
end
Sr[i] = (Sr[i] / T) * x[i]
S = Sr[i] + S
end
return -S+b
end
#dist = Distributions.Uniform(0.0,1.0)
#x0 = Distributions.rand(dist, K)
x0=zeros(K)
lb = [0.0, 0.0,0.0, 0.0, 0.0, 0.0, 0.0,0.0, 0.0, 0.0]
ub = [1.0, 1.0, 1.0,1.0, 1.0, 1.0, 1.0, 1.0,1.0, 1.0]
opt = NLopt.Opt(:GN_ISRES, K) #GN_ISRES LN_COBYLA
NLopt.lower_bounds!(opt,lb)
NLopt.upper_bounds!(opt,ub)
NLopt.xtol_rel!(opt, 1e-4)
NLopt.min_objective!(opt, yu)
NLopt.inequality_constraint!(opt,(x,g) -> ogrf1(x,g,1.0), 1e-6)
NLopt.inequality_constraint!(opt, (x,g) -> ogrf2(x,g,1.003), 1e-6)
min_f, min_x, ret = NLopt.optimize(opt, x0)
num_evals = NLopt.numevals(opt)
println(
"""
objective value : $min_f
solution : $min_x
solution status : $ret
# function evaluation : $num_evals
"""
)
@show round(ogrf1(min_x,[],1.0); digits=4)
@show round(ogrf2(min_x,[],1.001); digits=3)
@show round(sum(min_x);digits=4);
#ГРАФИК РЕШЕНИЯ GN_ISRES
using Plots, PlotThemes
plotly()
theme(:ggplot2)
X = 1:K
Y = min_x[1:K]*100
Yopt = -round(min_f; digits=5)
function bar1()
data = bar(X, Y, label="%")
plot(data, wsize=(950, 500))
ylabel!("Процет акций в портфеле")
xlabel!("Номер акции")
title!("xopt (алгоритм GN_ISRES),Yopt=$Yopt, K=$K, Ntime≈ 6мин 17с.")
end
bar1()
Имеем довольно интересный результат самое большое значение целевой функции получено методом Монте-Карло 0.01872, а самый низкий при помощи алгоритма локальной оптимизации LN_COBYLA 0.0177, алгоритм глобальной оптимизации GN_ISRES дал среднее значение целевой функции 0.01824. Предпологаю, что пространство имеет сложную топологию с большим числом случайно расположенных мало различимых локальных оптимов и LN_COBYLA выбирает один из таких локальных максимумов целевой функции, а GN_ISRES перебирает локальные max, стремясь найти глобальный max при этом затрачиваются значительные вычислительные ресурсы. Метод Mонте-Карло случайно прыгает из одной точки пространства в другую и это не требует больших вычислительных ресурсов.При этом удается найти довольно быстро один из хороших локальных мах целевой функции. Но самое главное, что LN_COBYLA и GN_ISRES прилично работают при решении таких довольно не тривиальных оптимизационных задач.
Задача 4:
Задача о рюкзаке (англ. Knapsack problem) — дано предметов, предмет имеет массу и стоимость . Необходимо выбрать из этих предметов такой набор, чтобы суммарная масса не превосходила заданной величины (вместимость рюкзака), а суммарная стоимость была максимальна.
Формулировка задачи
Дано предметов, — вместимость рюкзака, — соответствующий ему набор положительных весов предметов, - соответствующий ему набор положительных стоимостей предметов. нужно найти бинарный вектор
где , если предмет включен в набор, , если предмет не включен, и такой что:
Ниже представлен скрипт, решающий эту задачу с помощью с решателем
#задача линейной целочисленной бинарной оптимизации
using Distributions
using Random
L=15 # число предметов
Wogr=35 # вместимость рюкзака кг
# случайная генерация вектора весов w и вектора стоимостей pr
#Random.seed!(123) # обеспечение воспроизводимости результатов
dist1 = Distributions.Uniform(1.0,10.0)
dist2 = Distributions.Uniform(10.0,500.0)
w = Distributions.rand(dist1,L)
pr = Distributions.rand(dist2,L)
x=zeros(L)
#решение задачи
using JuMP, GLPK
model = Model(GLPK.Optimizer)
@variable(model, x[1:L],Bin)
@objective(model, Max,sum(x.*pr) )
@constraint(model,sum(x.*w)<= Wogr)
JuMP.optimize!(model)
#выдача результатов решения задачи
#@show value.(x)
#@show objective_value(model);
Price_max =round(sum(pr.*value.(x)); digits=2)
Xmax=(value.(x))
W=round(sum(Xmax.*w);digits=2)
println(" РЕЗУЛЬТАТЫ РЕШЕНИЯ ЗАДАЧИ О РЮКЗАКЕ ")
println("Вектор включения предметов в рюкзак: $Xmax")
println("Максимальная стоимость предметов в рюкзаке: $Price_max руб")
println("Вес предметов, включенных в рюкзак: $W кг")
Задача 5: Определение оптимального производства продукции
Предприятие производит видов продукции. План производства можно предствить в виде вектора . Здесь имеем плановый объем производства -го вида продукции. Для производства каждого вида продукции необходимы определенные ресурсы. Известно запасы каждого ресурса где -число видов ресурсов, , запас - го ресурса. При этом известны нормы расхода каждого ресурса на единицу каждого вида продукции, которые представим в виде матрицы: где - норма расхода -го ресурса на единицу -го продукта. Заданы также заданы нормы прибыли от каждого вида продукции где - прибыль от единицы продукции - го вида продукции.Коме того известен коэффициент отдачи прибыли .
Тогда задача определения оптимального плана производства имее следующий вид:
using JuMP,GLPK
a=1.0 # коэффициент отдачи прибыли-задача линейной оптимизации
n=5 # число видов ресурсов
m=3 # число видов продукции
R=collect([450.0,250.0,800.0,450.0,600.0]) # количество ресурсов
r=collect([1.0 1.0 1.0; 1.0 0.0 0.0; 2.0 2.0 1.0; 1.0 1.0 0.0; 2.0 1.0 1.0]) # нормы расхода ресурсов на единицу продукта
p=collect([75.0 50.0 35.0]) # прибыль на единицу продукции
model = Model(GLPK.Optimizer)
@variable(model, x[1:m]>=0)
for j in 1:n
@constraint(model, sum(r[j,i]*x[i] for i=1:m) <=R[j])
end
@objective(model, Max, sum(p[i]*x[i] for i=1:m))
JuMP.optimize!(model)
#@show value.(x)
#@show objective_value(model);
xmax=value.(x)
Pmax=sum(p[i]*xmax[i] for i=1:m)
Rp1 =:(sum(r[1,i]*xmax[i] for i=1:m))
Rp2 =:(sum(r[2,i]*xmax[i] for i=1:m))
Rp3 =:(sum(r[3,i]*xmax[i] for i=1:m))
Rp4 =:(sum(r[4,i]*xmax[i] for i=1:m))
Rp5 =:(sum(r[5,i]*xmax[i] for i=1:m))
println(" РЕЗУЛЬТАТЫ РЕШЕНИЯ ЗАДАЧИ ОБ ОПТИМАЛЬНОМ ПЛАНЕ ПРОИЗВОДСТВА a=$a ")
println("Оптимальные объемы производства: $xmax")
println("Максимальная прибыль: $Pmax руб")
Rp=[Rp1,Rp2,Rp3,Rp4,Rp5]
for j in 1:n
Rreal=eval(Rp[j])
Rzap=R[j]
Rost=Rzap-Rreal
println("Плановый расход ресурса $j: $Rreal ; Запасы: $Rzap ; Остаток: $Rost")
end
using JuMP,NLopt
a=0.85 # задача нелинейной оптимизации
n=5
m=3
R=collect([450.0,250.0,800.0,450.0,600.0])
r=collect([1.0 1.0 1.0; 1.0 0.0 0.0; 2.0 2.0 1.0; 1.0 1.0 0.0; 2.0 1.0 1.0])
p=collect([75.0 50.0 35.0])
model = Model(NLopt.Optimizer)
set_attribute(model, "algorithm", :LN_COBYLA)
set_attribute(model, "xtol_rel", 1e-4)
set_attribute(model, "constrtol_abs", 1e-4)
@variable(model, x[1:m]>=0)
set_start_value.(x,[100.0,100.0,20.0])
@NLobjective(model, Max, (sum(p[i]*x[i] for i=1:m))^a)
for j in 1:n
@constraint(model, sum(r[j,i]*x[i] for i=1:m) <=R[j])
end
JuMP.optimize!(model)
max_f, max_x, ret = objective_value(model), value.(x), raw_status(model)
println(
"""
objective value : $max_f
solution : $max_x
solution status : $ret
"""
)
Pmax=round(max_f;digits=2)
Rp1 =:(sum(r[1,i]*max_x[i] for i=1:m))
Rp2 =:(sum(r[2,i]*max_x[i] for i=1:m))
Rp3 =:(sum(r[3,i]*max_x[i] for i=1:m))
Rp4 =:(sum(r[4,i]*max_x[i] for i=1:m))
Rp5 =:(sum(r[5,i]*max_x[i] for i=1:m))
println(" РЕЗУЛЬТАТЫ РЕШЕНИЯ ЗАДАЧИ ОБ ОПТИМАЛЬНОМ ПЛАНЕ ПРОИЗВОДСТВА a=$a ")
println("Оптимальные объемы производства: $max_x")
println("Максимальная прибыль: $Pmax руб")
Rp=[Rp1,Rp2,Rp3,Rp4,Rp5]
for j in 1:n
Rreal=eval(Rp[j])
Rzap=R[j]
Rost=Rzap-Rreal
println("Плановый расход ресурса $j: $Rreal ; Запасы: $Rzap ; Остаток: $Rost")
end
Задача 6: Определение оптимального плана перевозок
Постановка задачи
Требуется минимизировать затраты на перевозку товаров от претприятий-производителей на торговые склады. Приэтом необходимо учесть возможности поставок каждого производителей при максимальном удовлетворении запросов потребителей. Товары могут поставляться с любого завода на любой склад, но стоимость доставкина большее расстояние будет большей. Необходимо определить объемы перевозок между каждым заводом и складом в соответствии с потребностями складов т и производственными мощностями заводов, при которыз транспортные расходы минимальны
Математическая модель
Введем обозначения:
- количество поставщиков;
- количество потребителей;
-номер поставщика,
-номер потребителя,
-искомое плановое количество перевозки от -го поставщика к -му потребителю;
- план поставок от -го поставщика всем потребителям: ;
- план поставок от -му потребителю от всех поставщиков: ;
- цена франко-склад единицы груза -го поставщика к -му потребителю;
- ограниченная мощность -го постащика;
-ограниченный спрос -го потребителя;
Модель экономико-математической постановки задачи будет выглядеть следующим образом:
Здесь (1) - целевая функция, а (2),(3),(4) - ограничения
using JuMP,GLPK
# Задача линейной оптимизации
n=3 #количество поставщиков
m=5 #количество потребителей
S=zeros(n)
C=zeros(m)
B=collect([310.0,260.0,280.0]) #мощность поставщиков
D=collect([180.0, 80.0,200.0, 160.0, 220.0]) #спрос потребителей
p=collect([10.0 8.0 6.0 5.0 4.0; 6.0 5.0 4.0 3.0 6.0; 3.0 4.0 5.0 5.0 9.0]) #стоимость перевозки единицы груза
model = Model(GLPK.Optimizer)
@variable(model, x[1:n,1:m]>=0)
for i in 1:n
@constraint(model, sum(x[i,j] for j=1:m) <=B[i])
end
for j in 1:m
@constraint(model, sum(x[i,j] for i=1:n) >=D[j])
end
@objective(model, Min, sum(sum(p[i,j]*x[i,j] for j=1:m) for i=1:n ))
JuMP.optimize!(model)
x_min=(value.(x))
Pmin=objective_value(model)
Pmin=round(Pmin;digits=2)
for i in 1:n
S[i] = sum(x_min[i,j] for j=1:m)
end
for j in 1:m
C[j] = sum(x_min[i,j] for i=1:n)
end
println(" РЕЗУЛЬТАТЫ РЕШЕНИЯ ЗАДАЧИ ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОГО ПЛАНА ПЕРЕВОЗОК ")
println("Оптимальные объемы перевозок: $x_min")
println("Минимальные затраты на перевозку грузов: $Pmin руб")
for i in 1:n
Splan=S[i]
Bpower=B[i]
Busag = Bpower-Splan
println("Плановые поставки поставщика $i $Splan ,мощность постащика: $Bpower , использование мощности: $Busag ")
end
for j in 1:m
Cplan=C[j]
Cemk=D[j]
Cusag = Cemk-Cplan
println("Плановые поставки потребителю $j $Cplan ,возможность потребителя: $Cemk , использование возможности: $Cusag ")
end
Задача 7: Планирование численности персонала (целочисленное программирование)
Описательная модель
Оъекты и показатели задачи:
- персонал;
- бригады, включающие персонал;
- конкретное количество сотрудников, необходимых для удовлетворения спроса на услуги компани в каждый день недели;
- ограничение по условиям работы в виде потребности в двух последовательных выходных днях;
- обеспечение выполения работ при минимальных расходах на заработную плату персонала.
Необходимо определить требуемое количество постоянных работников в каждой бригаде для удовлетворения спроса на работы при минимальных расходах на зарплату и минимальном количестве работников, если зарплата у всех одинакова.
Математическая модель.
Введем обозначения:
-количество бригад;
-номер бригады;
-искомое плановое количество работников в -ой бригаде;
-количество дней в неделе;
-порядковый номер дня недели: 1=воскресенье, 2 = понедельник,...,7= суббота;
-календарная матрица, где C_{i,j} = 1.0 -рабочий день, а C_{i,j} = 0.0 -выходной;
-общая потребность в персонале (все бригады) по дням недели;
-плановое количество персонала (все бригады) по дням недели ;
-дневная ставка зарплаты одного работника,однакова для всех;
-дневной фонд зарплаты всего персонала.
Необходимо найти при котором:
using JuMP,GLPK
# Задача линейной целочисленной оптимизации
n=7 #количество бригад
m=7 #количество дней в неделе
P=40.0 #дневная ставка работника
S=zeros(n)
B=collect([22,17,13,14,15,18,24]) #потребность в персонале по днем недели
c=collect([0 0 1 1 1 1 1; 1 0 0 1 1 1 1; 1 1 0 0 1 1 1; 1 1 1 0 0 1 1; 1 1 1 1 0 0 1; 1 1 1 1 1 0 0; 0 1 1 1 1 1 0]) #календарная матрица
model = Model(GLPK.Optimizer)
@variable(model, x[1:n],Int)
for j in 1:m
@constraint(model, sum(x[i]*c[i,j] for i=1:n) >= B[j])
end
@objective(model, Min, sum(P*x[i] for i=1:n))
JuMP.optimize!(model)
x_min=(value.(x))
Wmin=objective_value(model)
for j in 1:m
S[j] = sum(x_min[i]*c[i,j] for i=1:n)
end
println(" РЕЗУЛЬТАТЫ РЕШЕНИЯ ЗАДАЧИ: Планирование численности персонала ")
println("Оптимальная численность бригад: $x_min")
println("Минимальный дневной фонд зарплаты:: $Wmin руб")
for j in 1:m
Splan=S[j]
Spot=B[j]
Svp = Splan-Spot
println("Плановое количество работников в день $j $Splan ,потребности в работниках: $Spot , превышение потребности: $Svp ")
end
Задача 8: Определение оптимального плана затрат на рекламу
При разработке годового финансового плана деятельности фирмы необходимо определить расходы на рекламу для получения наибольшей прибыли. Проблемная система должна включать:
- планируемые показатели сокращенного баланса расходов, доходов и прибыли в разрезе кварталов года;
- модели причинно-следственных связей объемов продаж, доходов и прибыли в зависимости от затрат на рекламу.
Математическая модель
Введем следующие обозначения:
-индекс квартала года;
-заданный коэффициент сезонности по кварталам;
- заданная цена изделия;
- заданная себестоимость изделия;
-заданные затраты на торговый персонал по кварталам;
-искомые ежеквариальные затраты на рекламу;
- число продаж в -ый квартал;
- выручка от реализации в -ый квартал;
-себестоимость в -ый квартал;
-валовая прибыль в -ый квартал;
- косвенные затраты в -ый квартал;
- суммарные затраты в -ый квартал;
Profit_j =Gprofit_j-Szat_j - прибыль в -ый квартал;
- норма прибыли в -ый квартал.
На основе квартальных данных формируются годовые данные :
- число продаж в год;
- выручка за год;
-годовая себестоимость;
- валовая прибыль за год;
- затраты на персонал за год;
-затраты на рекламу за год;
-косвенные затраты за год;
-суммарные затраты за год;
-годовая прибыль фирмы;
- норма прибыли за год.
Тогда оптимизационная задача состоит в нахождении вектора , обеспечивающего выполнения условий (1) и (2):
#ЦЕЛЕВАЯ ФУНКЦИЯ
function PROFIT(x::Vector,grad::Vector)
#задание параметров
s=[0.9,1.1,0.8,1.2] #коэффициент сезонности по кварталам
Pr=40.0 #цена изделия
seb=25.0 #себестоимость изделия
global Tpers=[8000.0,8000.0,9000.0,9000.0] #затраты на торговый персонал
#задание массивов
global Sales = zeros(4)
global Gain = zeros(4)
global Cp = zeros(4)
global Gprofit = zeros(4)
global Kzat = zeros(4)
global Szat = zeros(4)
global Profit = zeros(4)
global Npof = zeros(4)
#расчет число продаж в год
for j in 1:4
Sales[j] =35*s[j]*(x[j]+3000.0)^0.5
end
global SALES=sum(Sales[j] for j=1:4)
#расчет выручки за год
for j in 1:4
Gain[j] =Sales[j]*Pr
end
global GAIN=sum(Gain[j] for j=1:4)
#расчет себестоимости за год
for j in 1:4
Cp[j] =Sales[j]*seb
end
global CP=sum(Cp[j] for j=1:4)
#расчет валовой прибыли за год
for j in 1:4
Gprofit[j] =Gain[j] - Cp[j]
end
global GPR=sum(Gprofit[j] for j=1:4)
#расчет затрат на персонал за год
global TP=sum(Tpers[j] for j=1:4)
#расчет затрат на рекламу за год
global X=sum(x[j] for j=1:4)
#расчет косвенных затрат за год
for j in 1:4
Kzat[j] =0.15*Gain[j]
end
global KZ=sum(Kzat[j] for j=1:4)
#расчет суммарных затрат за год
for j in 1:4
Szat[j]=Tpers[j] + x[j] + Kzat[j]
end
global SZ=sum(Szat[j] for j=1:4)
#расчет годовой прибыли фирмы
for j in 1:4
Profit[j] =Gprofit[j]-Szat[j]
end
global PROF=sum(Profit[j] for j=1:4)
#расчет годовой нормы прибыли фирмы
for j in 1:4
Npof[j] =Profit[j]/Gain[j]
end
global NP = PROF/GAIN
return -PROF
end
#ОГРАНИЧЕНИЕ
function ogr(x::Vector,grad::Vector,a)
return sum(x)-a
end
println("целевая функция и ограничение заданы")
using NLopt
x0=[10000.0, 10000.0, 10000.0, 10000.0]
opt = NLopt.Opt(:LN_COBYLA, 4) #GN_ISRES LN_COBYLA
NLopt.xtol_rel!(opt, 1e-4)
NLopt.min_objective!(opt, PROFIT)
NLopt.inequality_constraint!(opt,(x,g) -> ogr(x,g,40000.0), 1e-3)
min_f, min_x, ret = NLopt.optimize(opt, x0)
num_evals = NLopt.numevals(opt)
println("ОГРАНЕЧЕНИЕ ВЫПОЛНЯЕТСЯ")
@show ogr_min_x=sum(min_x);
println(" РЕЗУЛЬТАТЫ РЕШЕНИЯ ЗАДАЧИ: Определение оптимального плана затрат на рекламу ")
for j in 1:4
NormP= round(Npof[j]*100;digits=0)
Pfit = round(Profit[j];digits=2)
GAin = round(Gain[j];digits=2)
Sal = round(Sales[j];digits=0)
Gpr = round(Gprofit[j];digits=2)
println("$j квартал : прибыль $Pfit р., норма прибыли $NormP %, продажи $Sal шт., выручка $GAin р., вал прибыль $Gpr p.")
end
println()
for j in 1:4
Xr = round(min_x[j];digits=2)
cP = round(Cp[j];digits=2)
kZ = round(Kzat[j];digits=2)
sZ = round(Szat[j];digits=2)
tP = round(Tpers[j];digits=2)
println("$j квартал : зат.на рекламу $Xr р., себестоимость $cP p., кос.зат. $kZ p., сум.зат. $sZ р., зат на персонал $tP p. ")
end
println()
println(" ГОДОВЫЕ РЕЗУЛЬТАТЫ ДЕЯТЕЛЬНОСТИ ФИРМЫ ")
l1 = :(SALESg =round(SALES;digits=0))
l2 = :(GAINg=round(GAIN;digits=2))
l3 = :(CPg =round(CP;digits=2))
l4 = :(GPRg =round(GPR;digits=2))
l5 = :(TPg =round(TP;digits=2))
l6 = :(KZg =round(KZ;digits=2))
l7 = :(SZg =round(SZ;digits=2))
l8 = :(NPg =round(NP*100;digits=0))
PROFopt = round(PROF;digits=2)
Xopt = round(sum(min_x);digits=2)
println("Результаты оптимизации: Затраты на на рекламу $Xopt р., Оптимальная прибыль $PROFopt р.")
Namens =["число продаж= ","выручка= ","себестоимость= ","валовая прибыль= ","затраты на персонал= ","косвенные затраты= ",
"суммарные затраты= ","норма прибыли= "]
Znac =[l1,l2,l3,l4,l5,l6,l7,l8]
for i in 1:8
print(Namens[i])
println(eval(Znac[i]))
end
Задача 8: Оптимальное размещение свободных средств в банковские депозиты.
Фирма с достаточным собственным капиталом работает от собственного капитала и имеет на счете временно свободные денежные средства. Фирма инвестирует на время деньги в банк, покупая у него депозитные сертификаты, получая от этого определенные проценты. Задача состоит в том, чтобы на полугодовом интервале планирования разместить с наибольшей доходностью временно свободные денежные средства на расчетном счете в 1-,3-, и 6-месячные депозитные сертификаты с фиксированной доходностью. При этом должны быть обеспечены собственные потребности в средствах и страховой резерв (фиксированый неснижаемый остаток на расчетном счете).
Заданы:
- =400000.0 р.-начальная сумма на счете;
- = [75000.0 -10000.0 -20000.0 80000.0 50000.0 -15000.0 60000.0]
ежемесячные текущие расходы (минус-поступления); - =0.01 - ежемесячный доход от 1-мес. дипозита ;
- =0.04 - ежеквартальный доход от 3-мес. дипозита ;
- =0.09 - полугодовой доход от 6-мес. дипозита ;
- Hfix-100000 р.- ежемесячный неснижаемый остаток на счете (лимит сальдо).
Необходимо определить:
- - ежемесячные суммы вложений в 1-мес. дипозит;
- - ежеквартальные вложения в 3-мес. дипозит;
- - вложение в 6-мес. дипозит.
Предпологается, что суммы дипозитов и проценты возвращаются постнумерандо (в конце месяца), а инвестируются пренумерандо (в начале месяца).
Учитывая все вышесказанное, формально задачу можно представить так:
Здесь (1) - линейная целевая функция, (2)-(8) - линейные рекурентные ограничения задающие область допустимых значений , а (9) ограничения, определяющие экономически разумную зону поиска оптимального решения.
Попытаемся применить для решения задачи алгоритмы из библиотеки NLopt. Воспользуемся алгоритмом глобальной оптимизации, не требующим расчета производных - GN_ISRES. Так как по умолчанию алгоритм определяет минимум целевой функции, то нашу целевую функцию возмем со знаком минус, а также скоррректируем ограничения, приводя их к виду . Кроме того, искусственно введем нелинейность целевой функции, возведя ее в степень 1.0.
function dohod(x::Vector,grad::Vector)
ProzDip=[0.01,0.01,0.01,0.01,0.01,0.01,0.04,0.04,0.09]
Dohod = -(sum(ProzDip[j]*x[j] for j=1:9))^1.0
end
println("Целевая функция запущена")
function x_ogr1(x::Vector,grad::Vector,a)
h[1]=(S0-(x[1]+x[7]+x[9]+Rash[1]))
#println(h[1])
-h[1]+a
end
function x_ogr2(x::Vector,grad::Vector,a)
h[2]=( (h[1] + x[1] + x[1]* Dip1)-(x[2]+Rash[2]))
#println(h[2])
-h[2]+a
end
function x_ogr3(x::Vector,grad::Vector,a)
h[3]=((h[2]+ x[2] + x[2]* Dip1)-(x[3]+Rash[3]))
#println(h[3])
-h[3]+a
end
function x_ogr4(x::Vector,grad::Vector,a)
h[4]=((h[3] + x[3] + x[8]+ x[3]*Dip1 + x[8]*Dip3) - (x[4]+x[8] + Rash[4]))
#println(h[4])
-h[4]+a
end
function x_ogr5(x::Vector,grad::Vector,a)
h[5]=((h[4]+ x[4]+ x[4]*Dip1)-(x[5] + Rash[5]))
#println(h[5])
-h[5]+a
end
function x_ogr6(x::Vector,grad::Vector,a)
h[6]=((h[5] + x[5] + x[5]*Dip1) - (x[6] + Rash[6]))
#println(h[6])
-h[6]+a
end
function x_ogr7(x::Vector,grad::Vector,a)
h[7]=(h[6] + x[6]+ x[8] + x[9] + x[6]*Dip1+ x[8]*Dip3+x[9]*Dip6)-(Rash[7])
#println(h[7])
-h[7]+a
end
println("Ограничения сформированны")
using NLopt
x0=[100000.0, 100000.0, 100000.0, 100000.0, 100000.0, 100000.0, 10000.0, 10000.0, 10000.0]
global Dip1 =0.01 #доход от дипозита 1 мес.
global Dip3 =0.04 # доход от дипозита 3 мес.
global Dip6 =0.09 # доход от дипозита 6 мес.
global S0=400000.0 #начальная сумма
global h = zeros(7)#начальное значение сальдо
global Rash=[75000.0 -10000.0 -20000.0 80000.0 50000.0 -15000.0 60000.0] #месячные расходы
Xmax=zeros(9)
opt = NLopt.Opt(:GN_ISRES,9) #GN_ISRES LN_COBYLA
NLopt.lower_bounds!(opt, [0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0])
NLopt.upper_bounds!(opt, [200000.0,200000.0,200000.0,200000.0,200000.0,200000.0,200000.0,200000.0,200000.0])
NLopt.xtol_rel!(opt, 1e-3)
NLopt.min_objective!(opt, dohod)
NLopt.inequality_constraint!(opt,(x,g) -> x_ogr1(x,g,100000), 1e-2)
NLopt.inequality_constraint!(opt, (x,g) -> x_ogr2(x,g,100000), 1e-2)
NLopt.inequality_constraint!(opt, (x,g) -> x_ogr3(x,g,100000), 1e-2)
NLopt.inequality_constraint!(opt, (x,g) -> x_ogr4(x,g,100000), 1e-2)
NLopt.inequality_constraint!(opt, (x,g) -> x_ogr5(x,g,100000), 1e-2)
NLopt.inequality_constraint!(opt, (x,g) -> x_ogr6(x,g,100000), 1e-2)
NLopt.inequality_constraint!(opt, (x,g) -> x_ogr7(x,g,100000), 1e-2)
min_f, min_x, ret = NLopt.optimize(opt, x0)
num_evals = NLopt.numevals(opt)
println(
"""
solution status : $ret
function evaluation : $num_evals
"""
)
for i in 1:9
Xmax[i] =round(min_x[i];digits=2)
end
for i in 1:7
h[i] =round(h[i];digits=2)
end
DOHOD_max=-round(min_f;digits=2)
@show Xmax
@show DOHOD_max
@show h[1:6];
#ПРОВЕРКА РЕШЕНИЯ ПО НАЧАЛЬНОЙ СУММЕ НА СЧЕТЕ ФИРМЫ
S0ras= Xmax[1]+Xmax[7]+Xmax[9]+h[1]+Rash[1] #расчетная по результатам решения задачи начальная сумма
@show S0ras=round(S0ras;digits=1)
@show S0;#заданная начальная сумма
Решим задачу с помощью JuMP,GLPK. Соответствующий скрипт и результаты его работы представлены ниже.
using JuMP,GLPK
global Dip1 =0.01 #доход от дипозита 1 мес.
global Dip3 =0.04 # доход от дипозита 3 мес.
global Dip6 =0.09 # доход от дипозита 6 мес.
global S0=400000.0 #начальная сумма
global h = zeros(7)#начальное значение сальдо
global Rash=[75000.0 -10000.0 -20000.0 80000.0 50000.0 -15000.0 60000.0] #месячные расходы
global ProzDip=[0.01,0.01,0.01,0.01,0.01,0.01,0.04,0.04,0.09]
global X_max=zeros(9)
model = Model(GLPK.Optimizer)
@variable(model,0.0<=x[1:9]<=200000.0)
@constraint(model,(S0-(x[1]+x[7]+x[9]+Rash[1]))>=100000)
@constraint(model,(((S0-(x[1]+x[7]+x[9]+Rash[1])) + x[1] + x[1]* Dip1)-(x[2]+Rash[2]))>=100000)
@constraint(model,(((((S0-(x[1]+x[7]+x[9]+Rash[1])) + x[1] + x[1]* Dip1)-(x[2]+Rash[2]))+ x[2] + x[2]* Dip1)-(x[3]+Rash[3]))>=100000)
@constraint(model,(((((((S0-(x[1]+x[7]+x[9]+Rash[1])) + x[1] + x[1]* Dip1)-(x[2]+Rash[2]))+ x[2] + x[2]* Dip1)-(x[3]+Rash[3])) + x[3] + x[8]+ x[3]*Dip1 + x[8]*Dip3) - (x[4]+x[8] + Rash[4])) >=100000)
@constraint(model,(((((((((S0-(x[1]+x[7]+x[9]+Rash[1])) + x[1] + x[1]* Dip1)-(x[2]+Rash[2]))+ x[2] + x[2]* Dip1)-(x[3]+Rash[3])) + x[3] + x[8]+ x[3]*Dip1 + x[8]*Dip3) - (x[4]+x[8] + Rash[4]))+ x[4]+ x[4]*Dip1)-(x[5] + Rash[5]))>=100000 )
@constraint(model,(((((((((((S0-(x[1]+x[7]+x[9]+Rash[1])) + x[1] + x[1]* Dip1)-(x[2]+Rash[2]))+ x[2] + x[2]* Dip1)-(x[3]+Rash[3])) + x[3] + x[8]+ x[3]*Dip1 + x[8]*Dip3) - (x[4]+x[8] + Rash[4]))+ x[4]+ x[4]*Dip1)-(x[5] + Rash[5])) + x[5] + x[5]*Dip1) - (x[6] + Rash[6]))>=100000)
@constraint(model,((((((((((((S0-(x[1]+x[7]+x[9]+Rash[1])) + x[1] + x[1]* Dip1)-(x[2]+Rash[2]))+ x[2] + x[2]* Dip1)-(x[3]+Rash[3])) + x[3] + x[8]+ x[3]*Dip1 + x[8]*Dip3) - (x[4]+x[8] + Rash[4]))+ x[4]+ x[4]*Dip1)-(x[5] + Rash[5])) + x[5] + x[5]*Dip1) - (x[6] + Rash[6])) + x[6]+ x[8] + x[9] + x[6]*Dip1+ x[8]*Dip3+x[9]*Dip6)-(Rash[7]) >=100000)
@objective(model, Max, sum(ProzDip[j]*x[j] for j=1:9))
JuMP.optimize!(model)
X_max=(value.(x))
for i in 1:9
X_max[i] =round(X_max[i];digits=2)
end
DOHOD_max=objective_value(model)
DOHOD_max=round(DOHOD_max;digits=2)
@show X_max
@show DOHOD_max;
В результате расчетов по NLopt, GN_ISRES максимальный доход фирмы за полгода от депозитов может составить DOHOD_max=23981.41 р., а по расчетам JuMP, GLPK DOHOD_max =24017.19 р. То есть полученные результаты практически идентичны.
Задача 9 : "Задача коммивояжера"
Содержательная постановка задачи
Дана матрица расстояний между городами (таблица 1)
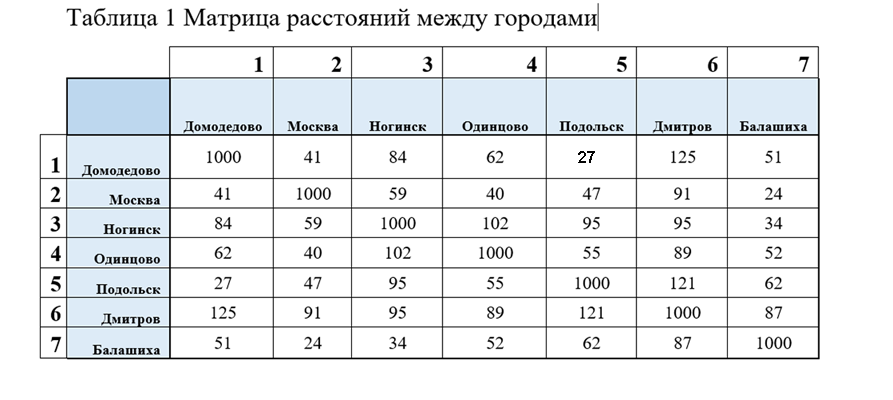
Нужно выехать из Домодедово и один раз посетить остальные города и вернуться в Домодедово. Необходимо найти такую последовательность посещения городов, при которой суммарная длина пройденного пути минимальна.
Математическая постановка задачи
Данная задача представляет собой задачу, состоящую в нахождении целых бинарных чисел , принадлежащих . Когда переезжаем из города в город - . Eсли, , то перехода между городами нет.
Введем город, расположенный в том же городе, где мы начинаем свое путешествие. Теперь из первого города можно только выйти, а в город можно только зайти. Дополнительное целочисленное значение равно количеству способов доступа к городу , .
Чтобы избежать замкнутых путей, нужно покинуть первый город и вернуться в . Определим дополнительные ограничения, которые связывают переменные и , - данный массив представляет собой количество всех городов, которые нужно объехать в каждый дискретной точке маршрута . Матрица состоит из расстояния между городами, где , . Задача называется симметричной, если = для всех и , то есть вес ребра на графе между двумя города не зависит от направления движения.
Математическая постановка задачи коммивояжера формулируется в нашем случае следующим образом:
где – конечное множество допустимых маршрутов, которое задается следующими ограничениями:
Решение задачи
#задача линейной бинарной оптимизации
using JuMP, GLPK
n=7
m=7
Gorod=["Домодедово","Москва","Ногинск","Одинцово","Подольск","Дмитров","Балашиха"]
r=[1000 41 84 62 27 125 51;41 1000 59 40 47 91 24;84 59 1000 102 95 95 34;
62 40 102 1000 55 89 52;27 47 95 55 1000 121 62;125 91 95 89 121 1000 87;
51 24 34 52 62 87 1000]
Xmin= [0 0 0 0 0 0 0;0 0 0 0 0 0 0;0 0 0 0 0 0 0;0 0 0 0 0 0 0;0 0 0 0 0 0 0;0 0 0 0 0 0 0;0 0 0 0 0 0 0]
model = Model(GLPK.Optimizer)
@variable(model, x[1:n,1:m],Bin)
@variable(model, u[1:n],Int)
@objective(model, Min, sum(sum(r[i,j]*x[i,j] for j=1:m) for i=1:n ))
for j in 1:m
@constraint(model, sum(x[i,j] for i=1:n) == 1)
end
for i in 1:n
@constraint(model, sum(x[i,j] for j=1:m) == 1)
end
for i in 1:n
@constraint(model, sum(x[i,i] for i=1:n) == 0)
end
@constraint(model,u[2]-u[2]+7*x[2,2] <=6 )
@constraint(model,u[3]-u[2]+7*x[3,2] <=6 )
@constraint(model,u[4]-u[2]+7*x[4,2] <=6 )
@constraint(model,u[2]-u[3]+7*x[2,3] <=6 )
@constraint(model,u[3]-u[3]+7*x[3,3] <=6 )
@constraint(model,u[4]-u[3]+7*x[4,3] <=6 )
@constraint(model,u[2]-u[4]+7*x[2,4] <=6 )
@constraint(model,u[3]-u[4]+7*x[3,4] <=6 )
@constraint(model,u[4]-u[4]+7*x[4,4] <=6 )
@constraint(model,u[2]-u[5]+7*x[2,5] <=6 )
@constraint(model,u[3]-u[5]+7*x[3,5] <=6 )
@constraint(model,u[4]-u[5]+7*x[4,5] <=6 )
@constraint(model,u[2]-u[6]+7*x[2,6] <=6 )
@constraint(model,u[3]-u[6]+7*x[3,6] <=6 )
@constraint(model,u[4]-u[6]+7*x[4,6] <=6 )
@constraint(model,u[2]-u[7]+7*x[2,7] <=6 )
@constraint(model,u[3]-u[7]+7*x[3,7] <=6 )
@constraint(model,u[4]-u[7]+7*x[4,7] <=6 )
@constraint(model,u[5]-u[2]+7*x[5,2] <=6 )
@constraint(model,u[6]-u[2]+7*x[6,2] <=6 )
@constraint(model,u[7]-u[2]+7*x[7,2] <=6 )
@constraint(model,u[5]-u[3]+7*x[5,3] <=6 )
@constraint(model,u[6]-u[3]+7*x[6,3] <=6 )
@constraint(model,u[7]-u[3]+7*x[7,3] <=6 )
@constraint(model,u[5]-u[4]+7*x[5,4] <=6 )
@constraint(model,u[6]-u[4]+7*x[6,4] <=6 )
@constraint(model,u[7]-u[4]+7*x[7,4] <=6 )
@constraint(model,u[5]-u[5]+7*x[5,5] <=6 )
@constraint(model,u[6]-u[5]+7*x[6,5] <=6 )
@constraint(model,u[7]-u[5]+7*x[7,5] <=6 )
@constraint(model,u[5]-u[6]+7*x[5,6] <=6 )
@constraint(model,u[6]-u[6]+7*x[6,6] <=6 )
@constraint(model,u[7]-u[6]+7*x[7,6] <=6 )
@constraint(model,u[5]-u[7]+7*x[5,7] <=6 )
@constraint(model,u[6]-u[7]+7*x[6,7] <=6 )
@constraint(model,u[7]-u[7]+7*x[7,7] <=6 )
JuMP.optimize!(model)
#выдача результатов решения задачи
Xmin=value.(x)
Xmin=Xmin'
j1=1
g1=Gorod[j1]
j2 =findfirst(==(1.0),Xmin[1,1:7])
g2=Gorod[j2]
j3 =findfirst(==(1.0),Xmin[j2,1:7])
g3=Gorod[j3]
j4 =findfirst(==(1.0),Xmin[j3,1:7])
g4=Gorod[j4]
j5 =findfirst(==(1.0),Xmin[j4,1:7])
g5=Gorod[j5]
j6 =findfirst(==(1.0),Xmin[j5,1:7])
g6=Gorod[j6]
j7 =findfirst(==(1.0),Xmin[j6,1:7])
g7=Gorod[j7]
j8=j1
g8=Gorod[j1]
Rmin = objective_value(model);
println(" Оптимальный маршрут: $g1.$j1-$g2.$j2-$g3.$j3-$g4.$j4-$g5.$j5-$g6.$j6-$g7.$j7-$g8.$j1")
println(" Rmin =$Rmin км.")
Задача 10 : «Ликвидация склада»
Содержательная постановка задачи
На предприятии 3 склада. Склад № 3 ликвидируется. Товары с 3 склада нужно перевезти на 1 и 2 склады таким образом, чтобы в результате стоимость товаров (в сумме) на 1 и 2 складах была одинаковой. При этом перемещать товары между 1 и 2 складами нельзя.
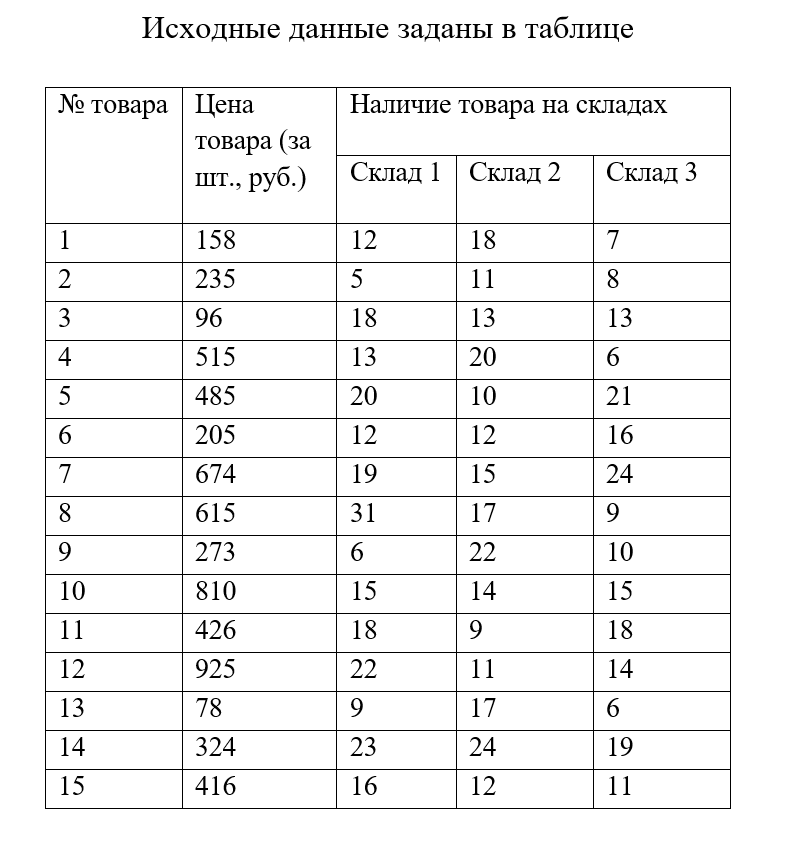
Математическая постановка задачи.
Сначала структурируем исходные данные до ликвидации склада 3, а затем сформируем данные после ликвидации склада 3. Графически мы изобразили это на рисунке 1.
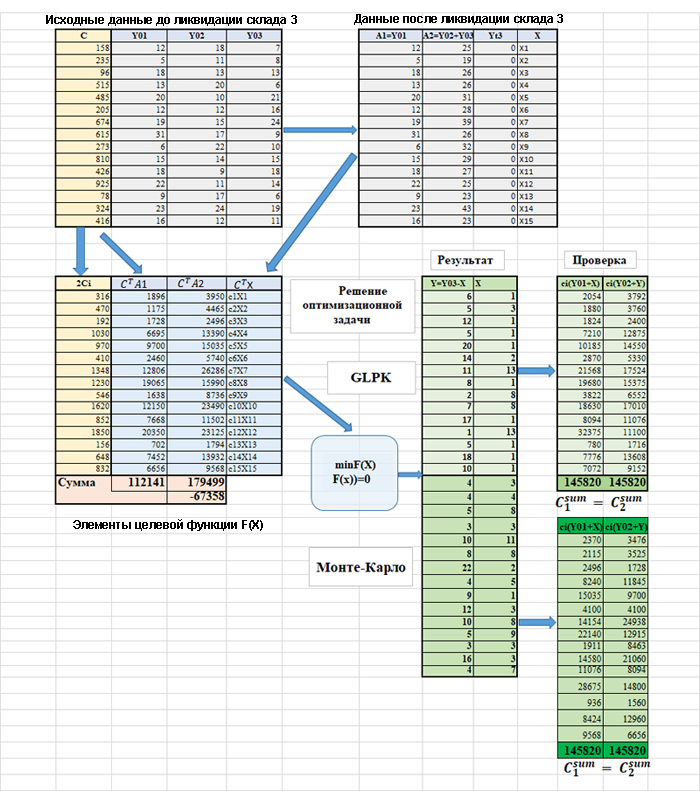
Рисунок 1 - Структура формирования элементов целевой функции
Здесь в блоке данных до ликвидации склада 3: – вектор столбец стоимостей единицы каждого товара; -вектор столбец количества каждого товара на первом складе; -вектор столбец количества каждого товара на втором складе; -вектор столбец количества каждого товара на третьем складе.
Введем вектор столбец , элементы которого представляют количество соответствующего товара перемещаемого с третьего склада на первый склад. Тогда можно сформировать данные после ликвидации третьего склада. Мы получаем: – вектор столбец констант для каждого товара, которые равны количеству соответствующего товара на складе 1 до ликвидации третьего склада; вектор столбец констант для каждого, которые равны количеству соответствующего товара на складе 2 до ликвидации третьего склада плюс количество каждого товара на складе 3 до его ликвидации (этот столбец получается из условия полной ликвидации склада 3); – пустой вектор столбец, получаемый для третьего склада после его ликвидации.
Теперь можно вести в рассмотрение следующие данные:
- - это постоянная суммарная стоимость товаров на складе 1;
- - это постоянная суммарная стоимость товаров на складе 2 с учетом ликвидации склада 3;
- - это дополнительная суммарная стоимость товаров на складе1 за счет ликвидации склада 3.
Для склада 2 эта величина должна браться с минусом так как для любого товара на склад 2 перемещается , где –количество -го товара, перемещаемого на второй склад; – количество -го товара, хранившегося на; - количество -го товара перемещаемого на первый склад;
Введенные величины позволяют получить следующие соотношения:
– это суммарная стоимость товаров на первом и втором складах после ликвидации 3-го склада. Исходя из условия задачи, формируем следующую целевую функцию:
Располагая рабочей целевой функцией сформулируем оптимизационную задачу следующим образом:
Т о есть, минимизировать функцию нужно до достижения целевой функции нулевого значения при следующих ограничениях:
Таким образом, необходимо минимизировать линейную целевую функцию при строгих ограничениях. То есть мы делаем дополнительное условие, что любой товар должен перемещаться в оба склада. Перед нами условная целочисленная оптимизации.Эту задачу можно решать классическими методами линейного целочисленного программирования и методом Монте-Карло. При решении методом целочисленной линейной оптимизации с использованием мы сталкиваемся с определенными сложностями. Алгоритм не работает со строгими ограничениями и не принимает abs в целевой функции. Для ограничений нижнюю границу пологаем равной 1, а верхнюю границу исходное значение минус 1. В целевой функции опускаем abs и вводим в качестве ограничения условие (это должно обеспечить равенство стоимостей товаров на 1 и 2 складах после ликвидации 3-го склада). Метод Монте -Карло реализуем с аналогичными ограничениями и для остановки минимизаци целевой функции используем условие .Ниже предствлены сооотвествующие скрипты и результаты их работы. На рисунке 1 показаны результаты проверки полученных решений.
#ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОГО ПЛАНА МЕТОДОМ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ GLPK
n=15
A0=-67358.0
A=[316.0 470.0 192.0 1030.0 970.0 410.0 1348.0 1230.0 546.0 1620.0 852.0 1850.0 156.0 648.0 832.0]
B=[7 8 13 6 21 16 24 9 10 15 18 14 6 19 11]
using JuMP, GLPK
model = Model(GLPK.Optimizer)
@variable(model, x[1:n],Int)
@objective(model, Min,(A0 + sum(A[i]*x[i] for i=1:n)))
for i in 1:n
@constraint(model, 1 <= x[i] <= B[i]-1)
end
@constraint(model,(A0 + sum(A[i]*x[i] for i=1:n))==0.0)
JuMP.optimize!(model)
@show value.(x)
@show objective_value(model);
#ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОГО ПЛАНА МЕТОДОМ МОНТЕ КАРЛО
using Distributions
using Random
N =1500000 #число итераций
Fmin=10^10
Xopt = [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
x=[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
n=15
A0=-67358.0
A=[316.0 470.0 192.0 1030.0 970.0 410.0 1348.0 1230.0 546.0 1620.0 852.0 1850.0 156.0 648.0 832.0]
B=[7 8 13 6 21 16 24 9 10 15 18 14 6 19 11]
Random.seed!(456)
for l in 1:N
for i in 1:n
x[i]=rand(1:(B[i]-1));
end
F =abs(A0+sum(A[i]*x[i] for i=1:n))
if F<Fmin
Fmin=F
println("Fmin = $Fmin Итерация = $l")
for i in 1:n
Xopt[i]=x[i]
end
end
if Fmin <=1.0
println("Итерация = $l")
break
end
end
println("Финишное значение Fmin = $Fmin")
println("Финишное значение Xopt= $Xopt")
Задача 11 : Классическая оптимизация портфеля ценных бумаг (ц/б).
Ранее мы расматривали аналогичную задачу в постановке Канемана-Тверски (теория перспектив). Здесь мы рассмотрим задачу нахождения оптимального портфеля ц/б в традиционной постановке.
Содержательная постановка
Банк, инвестиционная компания и т.д. формируют портфель ц/б клиента (инвестора). Инвестор имеет свободные денежные средства и хочет с них получить максимальную прибыль при минимальном риске. Но теория и практика финансовых рынков утверждает, что эти критерии противоречивы и желание увеличения прибыли сопровождается увеличением рисков. Поэтому, можно сформировать наилучший портфель акций клиента в смысле получения хорошей прибыли при небольшом риске.
Математическая модель
Согласно модели Шарпа доходность портфеля определяется следующим образом:
В (1):
- - доходность портфеля,%
- - доходность безрисковых активов, %
- - доходность рынка,%
- - бета портфеля -показатель системного, рыночного риска портфеля:
где
- - доля актива в портфеле;
- -бета -ой акции;
- - номер бумаги в портфеле;
- - количество бумаг в портфеле.
Риск портфеля определяется дисперсией доходности портфеля:
где
- - дисперсия доходности портфеля ;
- - дисперсия доходности рынка;
- - дисперсия доходности i-ой бумаги.
Исходными данными для расчета характеристик портфеля являются доходность безрисковых активов (), доходность рынка (), дисперсия доходности рынка , бета каждой акции , остаточная дисперсия каждой акции . При решении задачи ищутся доли акций в портфеле .
Задачи оптимизации портфеля
- Максимизация доходности портфеля при ограниченном риске (дисперсии доходности портфеля):
где -заданное инвестором ограничение риска портфеля в долях или процентах.
- Минимизация риска при заданном ограничении уровня доходности портфеля:
где - заданное инвестором ограничение по уровню доходности портфеля в долях или процентах.
Решим задачи (4) и (5) с использованием пакетов нелинейной оптимизации из экосистемы Julia. Соответствующие скрипты и результаты их работы приведены ниже.
#Максимизация доходности портфеля при ограниченном риске (4) JuMP, NLopt
#1. Исходные данные
n=5 #число акций в портфеле
Rf=0.06 # доходность без рисковых активов
Rm=0.15 # доходность рынка
Vm=0.03 # дисперсия доходности рынка
B=[0.80 1.00 1.80 2.20 0.0] # бета акций
V=[0.04 0.20 0.12 0.40 0.0] # дисперсии доходностей
Vb=0.07 # заданный уровень риска портфеля
# 2.Решение задачи
using JuMP, NLopt
model = Model(NLopt.Optimizer)
set_attribute(model, "algorithm", :LN_COBYLA)#GN_ISRES,LN_COBYLA
set_attribute(model, "xtol_rel", 1e-9)
set_attribute(model, "constrtol_abs", 1e-9)
@variable(model, 0.0<=x[1:n]<=1.0)
set_start_value.(x,[0.0,0.0,0.0,0.0,1.0])
@NLobjective(model, Max, (Rf+(Rm-Rf)*(sum(x[i]*B[i] for i=1:n))))
@NLconstraint(model, sum(x[i] for i=1:n) == 1.0)
@NLconstraint(model, ((Vm*((sum(x[i]*B[i] for i=1:n))^2) + sum(x[i]^2*V[i] for i=1:n)) <= Vb))
JuMP.optimize!(model)
# 3.Выдача результатов решения
max_f, max_x, ret = objective_value(model), value.(x), raw_status(model)
Rp_max=max_f
Rp_max=round(Rp_max; digits=2)
max_X=max_x
Vp_max=(Vm*((sum(max_X[i]*B[i] for i=1:n))^2) + sum(max_X[i]^2*V[i] for i=1:n))
for i in 1:n
max_X[i]=round(max_X[i];digits=2)
end
Vp_max=round(Vp_max; digits=2)
Ogr1=Vp_max<=Vb
Ogr2=sum(JuMP.value.(x))==1.0
println("Результаты решения задачи максимизации доходности портфеля при ограниченном риске")
println("Доходность портфеля =$Rp_max ; Риск портфеля =$Vp_max")
println("Доли акций в портфеле =$max_X ")
println("Ограничение 1: Vp_max<=Vb $Ogr1 ; Ограничение 2: ∑ max_X[i]==1.0 $Ogr2")
#ГРАФИК РЕШЕНИЯ JuMP, NLopt
using Plots, PlotThemes
plotly()
theme(:ggplot2)
Wmax=zeros(5)
N = 1:n
Rp_max =round(objective_value(model)*100;digits=1)
Wmax = max_X[1:n]*100
for i in 1:n
Wmax[i] = round(Wmax[i]; digits=1)
end
function bar1()
data = bar(N, Wmax, label="%")
plot(data, wsize=(750, 400))
ylabel!("Процет акций в портфеле")
xlabel!("Номер акции")
title!("Оптимальный портфель(JuMP, NLopt),Rp_max=$Rp_max, Vp_max=$Vp_max")
end
bar1()
#Максимизация доходности портфеля при ограниченном риске (4) JuMP, Ipopt
#1. Исходные данные
n=5 #число акций в портфеле
Rf=0.06 # доходность без рисковых активов
Rm=0.15 # доходность рынка
Vm=0.03 # дисперсия доходности рынка
B=[0.80 1.00 1.80 2.20 0.0] # бета акций
V=[0.04 0.20 0.12 0.40 0.0] # дисперсии доходностей
Vb=0.07 # заданный уровень риска портфеля
# 2.Решение задачи
using JuMP, Ipopt
max_X=zeros(5)
x0=[0.2,0.2,0.2,0.2,0.2]
model = Model(Ipopt.Optimizer)
set_silent(model)
@variable(model, x[i=1:5], start=x0[i])
@NLobjective(model, Max,Rf+(Rm-Rf)*(sum(x[i]*B[i] for i=1:n)))
@constraint(model, sum(x[i] for i=1:n) == 1.0)
@NLconstraint(model,((Vm*((sum(x[i]*B[i] for i=1:n))^2) + sum(x[i]^2*V[i] for i=1:n)) <= Vb))
JuMP.optimize!(model)
# 3.Выдача результатов решения
Rp_max=JuMP.objective_value(model)
Rp_max=round(Rp_max; digits=2)
max_X=JuMP.value.(x)
Vp_max=(Vm*((sum(max_X[i]*B[i] for i=1:n))^2) + sum(max_X[i]^2*V[i] for i=1:n))
Rp_max=round(Rp_max; digits=2)
for i in 1:n
max_X[i]=round(max_X[i];digits=2)
end
Vp_max=round(Vp_max; digits=2)
Ogr1=Vp_max<=Vb
Ogr2=sum(JuMP.value.(x))==1.0
println("Результаты решения задачи максимизации доходности портфеля при ограниченном риске")
println("Доходность портфеля =$Rp_max ; Риск портфеля =$Vp_max")
println("Доли акций в портфеле =$max_X ")
println("Ограничение 1: Vp_max<=Vb $Ogr1 ; Ограничение 2: ∑ max_X[i]==1.0 $Ogr2")
#ГРАФИК РЕШЕНИЯ JuMP, Ipopt
using Plots, PlotThemes
plotly()
theme(:ggplot2)
Wmax=zeros(5)
N = 1:n
Wmax = max_X[1:n]*100
function bar1()
data = bar(N, Wmax, label="%")
plot(data, wsize=(750, 400))
ylabel!("Процет акций в портфеле")
xlabel!("Номер акции")
title!("Оптимальный портфель (JuMP, Ipopt),Rp_max=$Rp_max, Vp_max=$Vp_max")
end
bar1()
# Минимизация риска при заданном ограничении уровня доходности портфеля JuMP, Ipopt
#1. Исходные данные
n=5 #число акций в портфеле
Rf=0.06 # доходность без рисковых активов
Rm=0.15 # доходность рынка
Vm=0.03 # дисперсия доходности рынка
B=[0.80 1.00 1.80 2.20 0.0] # бета акций
V=[0.04 0.20 0.12 0.40 0.0] # дисперсии доходностей
Rb=0.18 # заданный уровень доходности портфеля
# 2.Решение задачи
using JuMP, Ipopt
min_X=zeros(5)
x0=[0.2,0.2,0.2,0.2,0.2]
model = Model(Ipopt.Optimizer)
set_silent(model)
@variable(model, x[i=1:5], start=x0[i])
@NLobjective(model,Min,Vm*((sum(x[i]*B[i] for i=1:n))^2) + (sum(x[i]^2*V[i] for i=1:n)))
@constraint(model, sum(x[i] for i=1:n) == 1.0)
for i in 1:n
@constraint(model, x[i]>=0)
end
@constraint(model,(Rf+(Rm-Rf)*(sum(x[i]*B[i] for i=1:n)))>=Rb)
JuMP.optimize!(model)
# 3.Выдача результатов решения
min_X=JuMP.value.(x)
Rp_min=Rf+(Rm-Rf)*(sum(min_X[i]*B[i] for i=1:n))
Rp_min=round(Rp_min; digits=2)
Vp_min=JuMP.objective_value(model)
Rp_min=round(Rp_min; digits=2)
for i in 1:n
min_X[i]=round(min_X[i];digits=2)
end
Vp_min=round(Vp_min; digits=2)
Ogr1=Rp_min >=Rb
Ogr2=sum(JuMP.value.(x))==1.0
println("Результаты решения задачи минимизация риска при заданном ограничении уровня доходности портфеля")
println("Доходность портфеля =$Rp_min ; Риск портфеля =$Vp_min")
println("Доли акций в портфеле =$min_X ")
println("Ограничение 1: Rp_min >=Rb $Ogr1 ; Ограничение 2: ∑ min_X[i]==1.0 $Ogr2")
#ГРАФИК РЕШЕНИЯ JuMP, Ipopt
using Plots, PlotThemes
plotly()
theme(:ggplot2)
Wmin=zeros(5)
N = 1:n
Wmin = min_X[1:n]*100
function bar1()
data = bar(N, Wmin, label="%")
plot(data, wsize=(750, 400))
ylabel!("Процет акций в портфеле")
xlabel!("Номер акции")
title!("Оптимальный портфель(JuMP, Ipopt),Rp_min=$Rp_min,Vp_min=$Vp_min")
end
bar1()
# Минимизация риска при заданном ограничении уровня доходности портфеля JuMP, NLopt
#1. Исходные данные
n=5 #число акций в портфеле
Rf=0.06 # доходность без рисковых активов
Rm=0.15 # доходность рынка
Vm=0.03 # дисперсия доходности рынка
B=[0.80 1.00 1.80 2.20 0.0] # бета акций
V=[0.04 0.20 0.12 0.40 0.0] # дисперсии доходностей
Rb=0.08000# заданный уровень риска портфеля
# 2.Решение задачи
using JuMP, NLopt
model = Model(NLopt.Optimizer)
set_attribute(model, "algorithm", :LN_COBYLA)#GN_ISRES,LN_COBYLA
set_attribute(model, "xtol_rel", 1e-6)
set_attribute(model, "constrtol_abs", 1e-3)
@variable(model, 0.0<=x[1:n]<=1.0)
set_start_value.(x,[0.2,0.2,0.2,0.2,0.2])
@NLobjective(model, Min,Vm*((sum(x[i]*B[i] for i=1:n))^2) + (sum(x[i]^2*V[i] for i=1:n)))
@NLconstraint(model, sum(x[i] for i=1:n) == 1.0)
@NLconstraint(model,(Rf+(Rm-Rf)*(sum(x[i]*B[i] for i=1:n)))>=Rb)
JuMP.optimize!(model)
# 3.Выдача результатов решения
min_f, min_x, ret = objective_value(model), value.(x), raw_status(model)
min_X=min_x
Rp_min=Rf+(Rm-Rf)*(sum(min_X[i]*B[i] for i=1:n))
Rp_min=round(Rp_min; digits=2)
Vp_min=min_f
for i in 1:n
min_X[i]=round(min_X[i];digits=2)
end
Vp_min=round(Vp_min; digits=2)
Ogr1= 0.07999<=Rp_min<=Rb
Ogr2= 0.99999 <= sum(value.(x))<=1.0
println("Результаты решения задачи минимизации риска при заданном ограничении уровня доходности")
println("Доходность портфеля =$Rp_min ; Риск портфеля =$Vp_min")
println("Доли акций в портфеле =$min_X ")
println("Ограничение 1: Vp_min >=Rb $Ogr1 ; Ограничение 2: ∑ min_X[i]==1.0 $Ogr2")
#ГРАФИК РЕШЕНИЯ JuMP, NLopt
using Plots, PlotThemes
plotly()
theme(:ggplot2)
Wmin=zeros(5)
N = 1:n
Wmin = min_X[1:n]*100
function bar1()
data = bar(N, Wmin, label="%")
plot(data, wsize=(750, 400))
ylabel!("Процет акций в портфеле")
xlabel!("Номер акции")
title!("Оптимальный портфель(JuMP, NLopt),Rp_min=$Rp_min,Vp_min=$Vp_min")
end
bar1()
В рамках данной портфельной теории и в большенстве рыночных реалий доходность и риск чаще всего изменяются в одном направлении. Добиться экстремального улучшения одного из показателей без ухудшения другого не удается. Выше мы при решении задачи минимизации риска при заданном ограничении уровня доходности с помощью JuMP, Ipopt в качестве ограничения на доход портфеля взяли довольно высокий уровень Rb=18% в результате минимальный риск составил Vpmin=8%. При этом в пятый актив пакета (безрисковый) средства не вклыдываются. При решении задачи с помощью JuMP, NLopt, LN_COBYLA мы задали довольно низкий уровень ограничения дохода портфеля Rb=8% в результате минимальный риск практически нулевой. При этом 83% средств вкладываются в без рисковый актив. То есть, полученные результы достаточно хорошо описывают финансовые реалии рынка акций. Это демонстрирует возможности использования оптимизационных пакетов экосистемы Julia при решении подобных задач.
Задача 12 :
Имеется три системы противоздушной обороны , , . Противник применяет три типа бомбардировщиков , , . Система сбивает самолеты типа , , соотвественно с вероятностями 0.9, 0.4, 0.2; система сбивает самолеты типа , , соотвественно с вероятностями 0.3, 0.6, 0.8; система сбивает самолеты типа , , соотвественно с вероятностями 0.5, 0.7, 0.2. Найти нижнюю и верхнюю цены игры. Найти оптимальную стратегию применения противоздушной обороны и оптимальную цену игры. Найти оптимальную стратегию применения различных типов бомбардировщиков.
Матрица игры для системы обороны имеет вид:
Найдем нижнюю цену игры и верхнюю цену игры :
Рассмотрим стратегии для систем обороны:
где характерезует частоты применения каждой из систем обороны,
Для нахождения оптимальной стратегии нужно решить задачу линейного программирования с матрицей :
где и
Решая задачу линейного программирования (1), получаем и на основе которых рассчитываем оптимальную цену игры и в результате мы формируем оптимальную стратегию для систем обороны
Чтобы найти оптимальную стратегию для бомбардировщиков , нужно решить двойственную задачу линейного программирования с матрицей :
Получив решение задачи (2), для расчета делаем тоже, что делали для расчета
Ниже приведены скрипты Julia, которые позволяют решить в полном объеме задачу 12.
n=3
A=zeros(n)
B=zeros(n)
a=[0.9 0.4 0.2;0.3 0.6 0.8;0.5 0.7 0.2] #матрица игры
for i in 1:3
A[i] = min(a[i,1],a[i,2],a[i,3])
end
@show α=max(A[1],A[2],A[3]) #нижняя цена игры
for j in 1:3
B[j] = max(a[1,j],a[2,j],a[3,j])
end
@show β=min(B[1],B[2],B[3]) #верхняя цена игры
#определение оптимальной стратегии для систем обороны
using JuMP, GLPK
model = Model(GLPK.Optimizer)
@variable(model, x[1:n]>=0.0)
@objective(model, Min,sum(x[i] for i=1:n))
for j in 1:n
@constraint(model,(sum(a[i,j]*x[i] for i=1:n))>=1.0)
end
JuMP.optimize!(model)
value.(x)
objective_value(model);
zmin=objective_value(model)
xopt=value.(x)
@show νopt =1/zmin # оптимальная цена игры
@show p1opt =xopt[1]*νopt #оптимальная частота применения системы обороны № 1
@show p2opt =xopt[2]*νopt #оптимальная частота применения системы обороны № 2
@show p3opt =xopt[3]*νopt #оптимальная частота применения системы обороны № 3
Sso =[p1opt,p2opt,p3opt] # оптимальная стратегия для систем обороны
@show sum(Sso)
for i in 1:n
Sso[i]=round(Sso[i];digits=2)
end
P1opt =Sso[1]
P2opt =Sso[2]
P3opt =Sso[3];
#определение оптимальной стратегии для бомбардировщиков
a=[0.9 0.4 0.2;0.3 0.6 0.8;0.5 0.7 0.2] #матрица игры
using JuMP, GLPK
model = Model(GLPK.Optimizer)
@variable(model, y[1:n]>=0.0)
@objective(model, Max,sum(y[i] for i=1:n))
for i in 1:n
@constraint(model,(sum(a[i,j]*y[j] for j=1:n)) <= 1.0)
end
JuMP.optimize!(model)
value.(y)
objective_value(model)
zmax=objective_value(model)
yopt=value.(y)
@show ν1opt =1/zmax # оптимальная цена игры
@show q1opt =yopt[1]*ν1opt #оптимальная частота применения бомбардировщика № 1
@show q2opt =yopt[2]*ν1opt #оптимальная частота применения бомбардировщика № 2
@show q3opt =yopt[3]*ν1opt #оптимальная частота применения бомбардировщика № 3
@show Sb =[q1opt,q2opt,q3opt] # оптимальная стратегия для самолетов
@show sum(Sb)
for i in 1:n
Sb[i]=round(Sb[i];digits=2)
end
Q1opt =Sb[1]
Q2opt =Sb[2]
Q3opt =Sb[3];
Vopt=round(ν1opt;digits=2)
println("Расчетные оптимальные стратегии сторон игры")
println("Оптимальная стратегия для систем обороны: Sso1/$P1opt ,Sso2/$P2opt ,Sso3/$P3opt ")
println("Оптимальная стратегия для бомбардировщиков; Sb1/$Q1opt, Sb2/$Q2opt ,Sb3/$Q3opt")
println("нижняя цена игры:α= $α ; верхняя цена игры: β= $β ")
println("Оптимальная цена игры: νopt=ν1opt=$Vopt ")
Расмотренные в данной работе примеры решения оптимизационных задач продемонстрировали большие возможности экосистемы Julia для её использования в качестве эффективного инструмента оптимизации. При этом рассмотрены различные классы таких задач: одномерная и многомерная оптимизация;безусловная и условная оптимизация; линейная и нелинейная оптимизация; целочисленная и бинарная оптимизация. Для решения столь разнообразных задач мы использовали небольшое число библиотек и алгоритмов оптимизации, доступных в Julia, делая акцент на простоту их использования, в частности мы старались использовать алгоритмы, не требующие производных, что часто упрощает их использования для специалистов,не имеющих математической подготовке в области методов оптимизации.
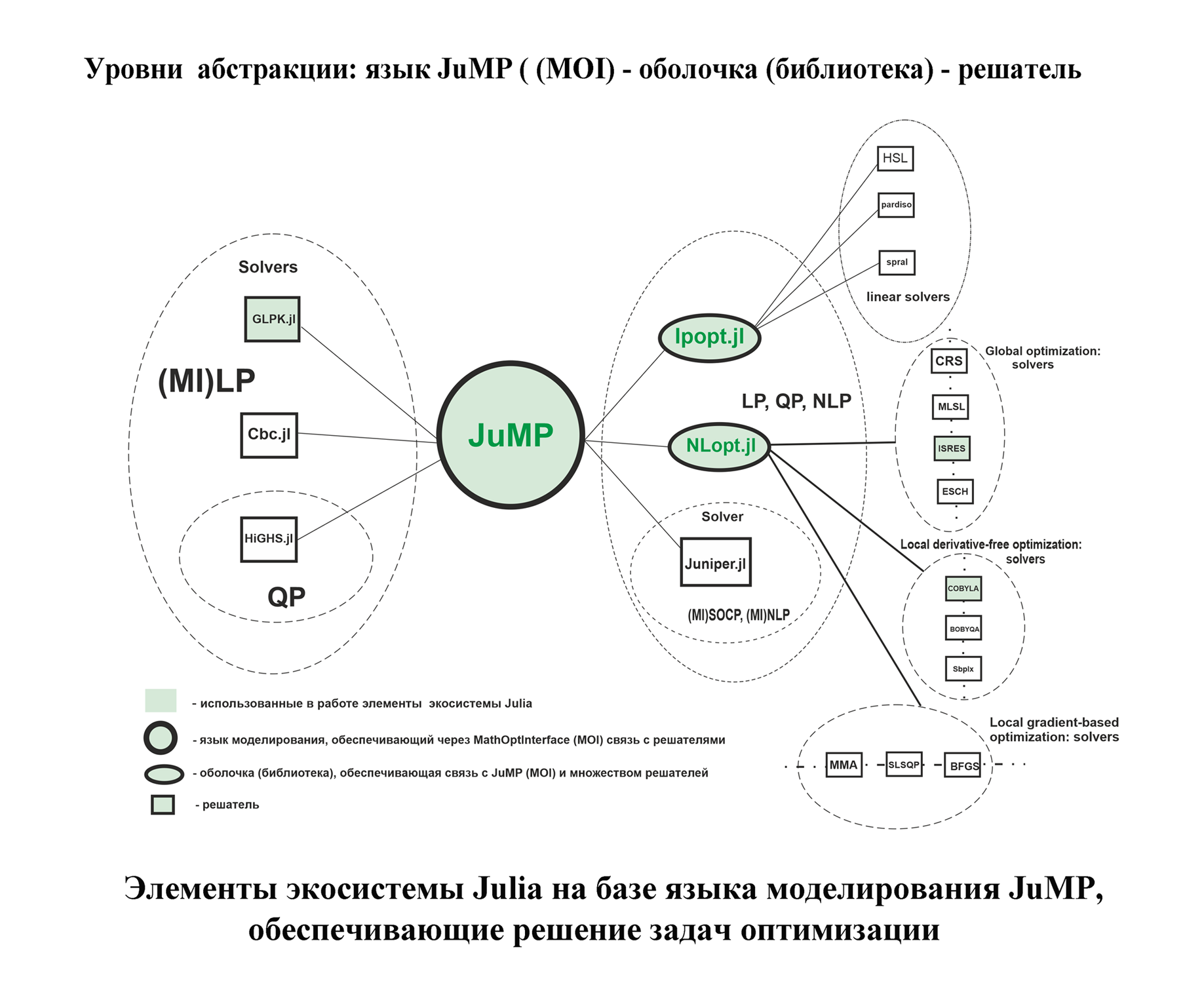
Приложения: Структура экосистемы Julia для решения задач оптимизации на базе JuMP и дополнительные пакеты.
Ниже представлен фрагмент экосистемы Julia для решения оптимизационных задач на базе JuMP. Использованные выше в нашей работе элементы, отмечены зеленым цветом. Несмотря на то,что их немного они позволяют решать очень широкий набор классов оптимизационных задач: линейное программирование (LP); смешанное целочисленное линейное программирование (MI)LP; квадратичное программирование (QP);нелинейная оптимизация NLP. При этом мы отбирали решатели, поддерживающие все виды ограничений (линейные,нелинейные, равенства и неравенства.) Остался неохваченным пожалуй только один важный для нас тип задач оптимизации: смешанное целочисленное нелинейное программирование (MI)NLP.Чтобы восполнить этот пробел мы установили пакет Juniper,который совместно с Ipopt, решает подобный тип задач. Кроме того мы попробовали еще два линейных решателя: HiGHS,Cbc. Простые примеры использования использования этих пакетов прведены ниже.
#Целочисленное линейное программирование:
#-2x[1] + x[4] + x[5]=1
#x[1] + x[2] - 2x[4]=2
#x[1] + x[3] +3x[4]=3
# x[1],x[2],...x[5]>=0; x[1],x[2],...x[5] -Int
#z=-x[1] +x[4] min
using JuMP, HiGHS
model = Model(HiGHS.Optimizer)
set_attribute(model, "presolve", "on")
set_attribute(model, "time_limit", 60.0)
@variable(model, x[1:5] >= 0,Int)
@constraint(model,-2x[1] + x[4] + x[5]==1)
@constraint(model,x[1] + x[2] - 2x[4]==2)
@constraint(model,x[1] + x[3] +3x[4]==3)
@objective(model, Min,-x[1] +x[4])
JuMP.optimize!(model)
@show JuMP.value.(x)
@show JuMP.objective_value(model);
using JuMP, Cbc
model = Model(Cbc.Optimizer)
set_attribute(model, "logLevel", 1)
@variable(model, x[1:5] >= 0,Int)
@constraint(model,-2x[1] + x[4] + x[5]==1)
@constraint(model,x[1] + x[2] - 2x[4]==2)
@constraint(model,x[1] + x[3] +3x[4]==3)
@objective(model, Min,-x[1] +x[4])
JuMP.optimize!(model)
@show JuMP.value.(x)
@show JuMP.objective_value(model);
#Juniper (MI)SOCP, (MI)NLP решение нелинейных целочисленных задач
using JuMP, Juniper, Ipopt
ipopt = optimizer_with_attributes(Ipopt.Optimizer, "print_level"=>0)
optimizer = optimizer_with_attributes(Juniper.Optimizer, "nl_solver"=>ipopt)
model = Model(optimizer)
v = [10, 20, 12, 23, 42]
w = [12, 45, 12, 22, 21]
@variable(model, x[1:5], Bin)
@objective(model, Max, v' * x)
@constraint(model, sum(w[i]*x[i]^2 for i in 1:5) <= 45)
JuMP.optimize!(model)
println(termination_status(model))
println(objective_value(model))
println(value.(x))
# Нелинейное программирование с линейными ограничениями:
#Дробно-линейное программирование
using JuMP, Ipopt
min_X=zeros(3)
x0=[0.0,0.0,0.0]
model = Model(Ipopt.Optimizer)
set_silent(model)
@variable(model, x[i=1:3], start=x0[i])
@NLobjective(model,Min,(-2x[1]+x[2])/(x[1]+2x[2] +1))
@constraint(model,(x[1]-2x[2])<=2.0)
@constraint(model,(2x[1]+x[2]+x[3])==6.0)
for i in 1:3
@constraint(model, x[i]>=0)
end
JuMP.optimize!(model)
min_X=JuMP.value.(x)
z_min=JuMP.objective_value(model)
z_min=round(z_min; digits=2)
for i in 1:3
min_X[i]=round(min_X[i];digits=3)
end
@show z_min
@show min_X;
#Дробно-линейное программирование
using JuMP, Juniper, Ipopt
min_X=zeros(3)
x0=[0.0,0.0,0.0]
ipopt = optimizer_with_attributes(Ipopt.Optimizer, "print_level"=>0)
optimizer = optimizer_with_attributes(Juniper.Optimizer, "nl_solver"=>ipopt)
model = Model(optimizer)
@variable(model, x[i=1:3], start=x0[i])
@NLobjective(model,Min,(-2x[1]+x[2])/(x[1]+2x[2] +1))
@constraint(model,(x[1]-2x[2])<=2.0)
@constraint(model,(2x[1]+x[2]+x[3])==6.0)
for i in 1:3
@constraint(model, x[i]>=0)
end
JuMP.optimize!(model)
min_X=JuMP.value.(x)
z_min=JuMP.objective_value(model)
z_min=round(z_min; digits=2)
for i in 1:3
min_X[i]=round(min_X[i];digits=3)
end
@show z_min
@show min_X;
#Квадратичное программирование
using JuMP, Ipopt
min_X=zeros(2)
x0=[0.0,0.0]
model = Model(Ipopt.Optimizer)
set_silent(model)
@variable(model, x[i=1:2], start=x0[i])
@NLobjective(model,Min,(x[1]^2 + 2x[2]^2 - 2x[1]*x[2] -2x[1]-6x[2]))
@constraint(model,(x[1]+x[2])<=2.0)
@constraint(model,(-x[1]+2x[2])<=2.0)
for i in 1:2
@constraint(model, x[i]>=0)
end
JuMP.optimize!(model)
min_X=JuMP.value.(x)
z_min=JuMP.objective_value(model)
z_min=round(z_min; digits=2)
for i in 1:2
min_X[i]=round(min_X[i];digits=3)
end
@show z_min
@show min_X;
using JuMP, Juniper, Ipopt #использование Juniper для решения
min_X=zeros(2)
x0=[0.0,0.0]
ipopt = optimizer_with_attributes(Ipopt.Optimizer, "print_level"=>0)
optimizer = optimizer_with_attributes(Juniper.Optimizer, "nl_solver"=>ipopt)
model = Model(optimizer)
set_silent(model)
@variable(model, x[i=1:2], start=x0[i])
@NLobjective(model,Min,(x[1]^2 + 2x[2]^2 - 2x[1]*x[2] -2x[1]-6x[2]))
@constraint(model,(x[1]+x[2])<=2.0)
@constraint(model,(-x[1]+2x[2])<=2.0)
for i in 1:2
@constraint(model, x[i]>=0)
end
JuMP.optimize!(model)
min_X=JuMP.value.(x)
z_min=JuMP.objective_value(model)
z_min=round(z_min; digits=2)
for i in 1:2
min_X[i]=round(min_X[i];digits=3)
end
@show z_min
@show min_X;